灰狼优化算法求解任务分配问题
朱 凡 谢亮亮
([1]江西机电职业技术学院 江西·南昌 330000;[2]江西银行股份有限公司 江西·南昌 330000)
0 引言
任务分配问题是一类典型的组合优化问题,它的优化目标是确定合理的子任务分配方案使所有任务的总完成时间最短。在问题规模较大和规定时间范围内寻找到问题的满意解。
很多启发式算法都是是对自然现象的模拟,其中灰狼优化算法(GWO)就是2012年Mirjalili S提出的一种通过模拟自然界中灰狼种群捕食过程的新型元启发式算法。GWO是通过设定合适的适应度函数就能使目标函数达到最优解。目前,GWO应用范围广泛,但还没有将其应用于求解任务分配问题。因GWO原理简单、需调整的参数少、易于实现、全局搜索能力强等特点,本文尝试将其应用于解决任务分配问题。
1 任务分配问题的数学描述

式中,(1)表示每个工人要执行一项任务;(2)表示每项任务被执行且被执行一次;(3)表示分配方案的元素值只能取0或者1。
2 灰狼优化算法(GWO)
GWO是一种随机全局优化方法,灵感来自于自然界中的灰狼种群的领导等级和狩猎机制。具体原理如下:
2.1 灰狼的等级划分
在GWO中,灰狼群有社会等级层次这样一个特殊点和群体狩猎的另一个特定社会行为。一般被分为四层,是狼群中适应度最佳的狼称为领导者,是狼群中适应度次最佳的狼称作下属狼负责帮助做决策或一些其他的活动,是狼群中适应度第三优的狼,它服从于是狼群中等级最低的狼且被比它等级高的狼所控制。
2.2 灰狼围住猎物模型
灰狼群在狩猎的时候,首先要对猎物进行跟踪,之后追逐猎物,接着赶上猎物进而团团围住猎物。此时的数学模型公式为如下所示:

2.3 狩猎数学模型
在GWO中狩猎行为就是数学中的优化操作,这时主要由灰狼群中前三个等级引导,而灰狼跟随着前三个等级的狼。当灰狼群团团围住猎物,进而骚扰猎物,直到猎物停下,最后开始攻击猎物,执行狩猎行为。这个行为通常是领导者带领一同参与。
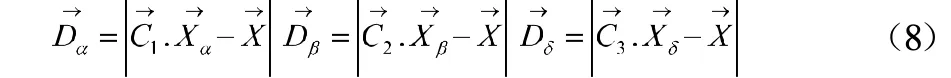
2.4 确定位置攻击猎物
狼群会根据猎物所停住的位置进行锁定,进而开始发动攻击来完成狩猎活动。为了靠近猎物,在模型中设定的值并减小,因此的值会因为而减小了。也就是说,在解决具体问题的时候,的值会从2减小到0,则是范围内的随机一个值。如果的值在[-1,1]内,猎物和灰狼的当前的位置之间的任意位置就是灰狼的下一个位置。灰狼对猎物发起攻击时是小于1的。
2.5 搜寻猎物
GWO是从狼群的随机创建到四个等级的狼群划分并预测猎物的位置,进而实现狼群中所有狼与猎物的新距离。从公式(6)中a的值的改变来判定GWO的全局搜索能力,从的取值来确定狼群与猎物距离的远近,最后达到结束条件,得到GWO优化后的最优解。
3 用GWO算法求解任务分配问题
简单的任务分配问题是给出两列元素及任意两列元素配对时的代价,找到1组一对一的配对使其代价和最小。设一列,表示工人编号,另一列,表示任务编号;一对一的分配表示每个工人被分配到1项任务,且不同的工人与不同的任务相配,,表示给工人分配任务时的代价。狼群的狩猎过程包括:跟踪,追逐,接近猎物;追赶包围,骚扰猎物直到它们停下;攻击。设有只狼,用狼群捕食来表示任务分配,每只灰狼代表决策变量的1个可能取值,每只灰狼的位置初始随机生成,记录下灰狼的初始位置;之后捕食猎物时,再记录下每只灰狼到达自己能最好攻击猎物位置。把任务分配问题与灰狼优化算法联系起来,是要每只灰狼快速到达自己该达到的位置以攻击猎物,最终在最短时间内捕食到猎物,正如每个工人在最快时间内完成自己的任务,以至于最后的总代价最小。
由于任务无先后之分,工人无主次之分,为使算法更具一般性,每只狼的位置由不同工人、不同任务得到,不妨令灰狼离猎物的最佳攻击位置为某个工人做某项任务的代价。由此可得任务分配问题的灰狼优化算法描述如下:
(2)适应度计算:适应度函数用于评价个体的优劣程度,适应度越大个体越好,反之适应度越小则个体越差;适应度函数是由目标函数来设定的,在GWO中也是区分狼群中个体层次的标准。在GWO中,需要计算每只灰狼的适应度,适应度函数用公式(12)表示:
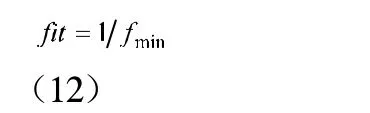
则取适应值前三的灰狼为:
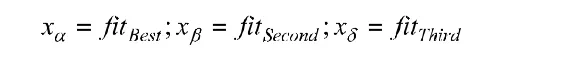
4 实验仿真与分析
本文仿真实验采用的实验环境有软硬件两个部分。软件部分采用的工具为 Matlab-R2009a,硬件部分 PC机型号是ACER 4752G,Intel Core 2 i3-2350M处理器,4G内存。用多维矩阵进行了大量的仿真验证,并把GWO与传统的匈牙利算法进行比较,结果如表1所示。
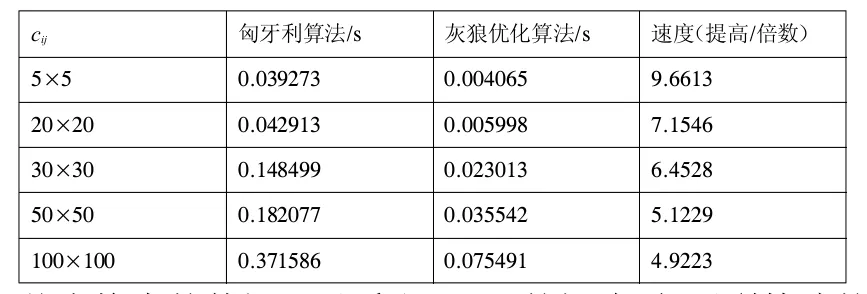
表1:算法的求解时闻与优化结果比较
从表格中的数据可以看出:5×5的矩阵,匈牙利算法的速度为0.039273/s,本文GWO算法为0.004065/s,提速9.6613倍。50×50的矩阵,匈牙利算法的速度为0.182077/s,本文GWO算法为0.035542/s,提速5.1229倍。100×100的矩阵,匈牙利算法的速度为0.371586/s,本文GWO算法为0.075491/s,提速4.9223倍。分析仿真结果,得出结论:本文算法GWO的计算速度明显高于匈牙利算法。但随着矩阵维数的增加,两者计算速度的倍数也在减小,从而说明GWO的稳定性有待加强。
5 结束语
虽然灰狼优化算法出现的时间没有其他智能算法长,但它已显示出求解优化问题的优势。本文综合任务分配的理论与实际意义,针对任务分配问题首次运用了GWO,仿真结果证明效果良好。

