低温压缩机角接触球轴承热特性研究*

（中国空气动力研究与发展中心）

0 引言

轴承是转动机械的重要零部件，起到支撑轴系的关键作用。滚动轴承尺寸紧凑、维护便捷，在小型转子系统中应用广泛。

航空发动机、高速机床、高速压缩机等机械装备的轴承常常在DN值大于1e6mm·r/min的工况运行，根据航空发动机的运行数据和失效分析结果，轴承打滑蹭伤和摩擦磨损所导致的故障比例高达53.89%。打滑蹭伤和摩擦直接加剧轴承生热，如果缺少有效的润滑和冷却，轴承产生的摩擦热不能有效地散发出去，必将造成轴承发热失效，如套圈滚道和滚动体回火或烧伤、保持架受热融化等[1]。特别是对于受限空间内的脂润滑滚动轴承，冷却条件较恶劣。

因此，轴承的温升问题一直是高速脂润滑滚动轴承亟待解决的突出问题。探明脂润滑滚动轴承的发热机理、传热特性以及温度分布，进而优化设计方案，有利于提高轴承的寿命和运行可靠性[2]。

滚动轴承的发热与轴承转速、载荷、润滑及冷却条件、安装布置情况、工作环境等因素密切相关[2～4]。Palmgren[5]基于试验测量提出了滚动轴承的整体载荷摩擦力矩和黏性摩擦力矩的经验公式。Harris[6]提出了球轴承和滚子轴承局部热源的计算方法。Rumbarger[7]等人按照Harris的分析思想对高速圆柱滚子轴承进行了热分析。国内也有很多学者针对滚动轴承的生热和传热特性进行了理论研究[8～11]，对于轴承的安全运行和优化设计工作具有积极意义。

本文针对某型低温压缩机的脂润滑角接触滚动轴承进行热特性研究，首先基于Palmgren参数化生热模型和热阻网格模型，计算得到轴承在不同工况下的温度分布，然后将常温工况和低温工况下的试验数据与理论计算结果进行对比，取得了较好的一致性，研究表明本文建立的模型具有较好的适用性，并验证了采用低温密封气强制冷却和电加热方案在脂润滑高速轴承控温方面的可行性。

1 轴承温度计算

1.1 结构参数

某型二级轴流式低温压缩机[12～13]介质温度范围110～323K，转速区间范围0～7 900r/min，压缩机的推力轴承为FAG公司的B7217-C-T-P4S型角接触轴承[14]，轴承采用脂润滑，常温运行时借助密封气辅助冷却，低温运行时借助电加热片辅助保温[12]。轴承安装实物如图1所示，主要参数如表1所示。

图1 某型压缩机轴承实物Fig.1 Rolling bearing of a compressor

表1 轴承参数Tab.1 Bearing parameters

1.2 生热计算

在工程实际中，轴承的发热主要来自载荷摩擦力矩和润滑剂粘性摩擦力矩等。Palmgren[5]基于对轴承摩擦力矩的测量结果，提出轴承的总摩擦力矩为：

式中，M0为轴承类型、转速和润滑剂性质有关的粘性摩擦力矩，N·mm；M1为与轴承所受负荷有关的摩擦力矩，N·mm。

摩擦力矩由以下各式联立求解[5，8，11]。

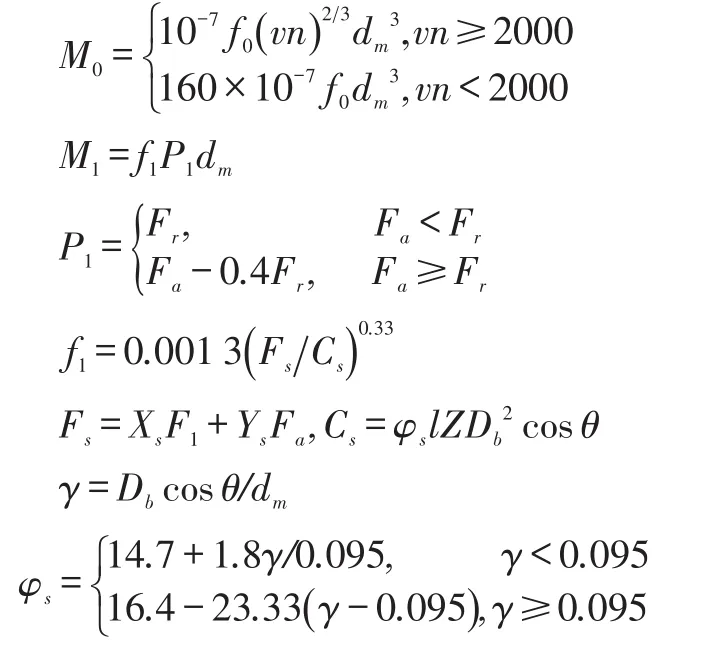
式中，dm为轴承节圆直径，mm；f0为与润滑方式有关数，对于脂润滑，f0=1～2；n为转速，r/min；v为润滑剂运动粘度mm2/s；f1为与轴承类型和所受载荷有关的系数；P1为轴承摩擦力矩的计算载荷；Fa为轴向载荷，N；Fr为径向载荷，N；Fs为当量载荷，N；Xs，Ys为当量载荷系数；Cs为基本额定静载荷，N；φs为载荷额定系数；l为列数；Z为球体个数；Db为球体直径，mm；θ为接触角。

此外，球轴承运转属于外滚道控制[15]，球与外圈无自旋分量，球与内圈的自旋力矩为。

式中，μ为球与滚道之间的滑动摩擦系数；Q为球与滚道法向接触载荷，N；a为赫兹接触椭圆长半轴，mm；ε为第二类椭圆积分。

发热功率为摩擦力矩和相应转速的乘积，发热量的内、外圈分量为[16]：

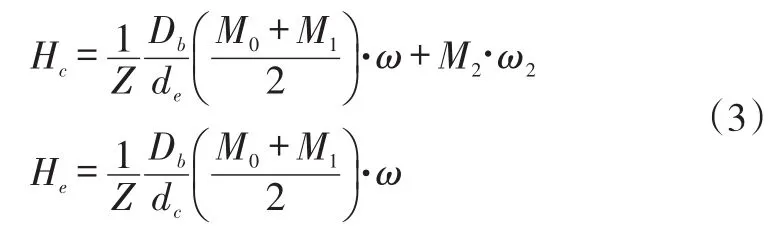
式中，dc和de分别为轴承内、外圈滚道直径。

采用Burton和Staph的建议[17]，一半的发热量进入球，另一半进入套圈。

1.3 传热计算

摩擦生热通过轴承、主轴、轴承座向外传递，这一过程可以用热阻网络来表示。实际的传热模型是三维的，由于结构是对称回转的，因此可以使用一维简化模型来表示。轴承一维模型如图2所示。

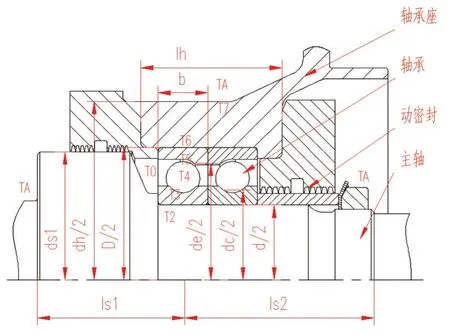
图2 轴承剖面图及尺寸Fig.2 Bearing 1-D profile and size

由于润滑脂的加入量较少，不考虑润滑脂的热传导作用。绘制热阻网络图如图3所示。图中各个热阻值的计算公式列于表2中，几何尺寸如图2所示，kc，ke，ks，kh分别为内圈、外圈、主轴、轴承座的导热系数，由材料特性决定，hc，he，hs，hh，hb分别为内圈、外圈、主轴、轴承座、钢球的对流换热系数。

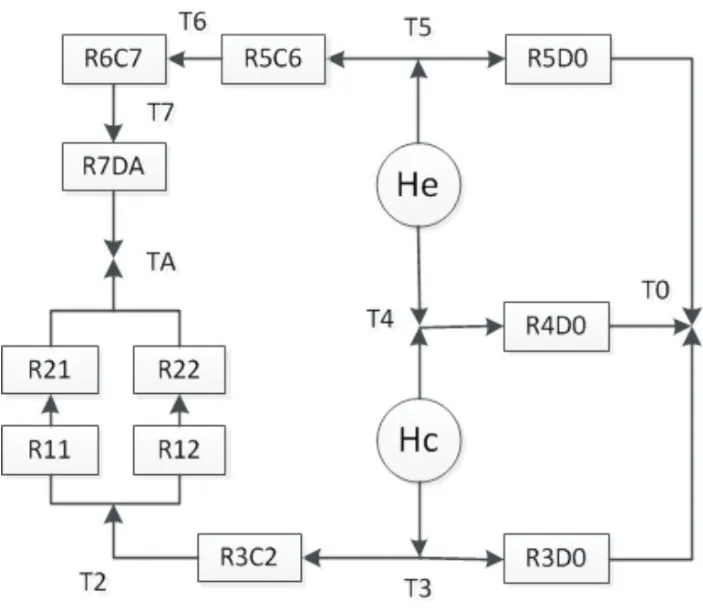
图3 轴承热阻网格Fig.3 Bearing thermal resistance grid

对流换热系数与普朗特数、粘度、导热系数、流动速度等因素有关，一般根据经验公式确定[11，18]。

式中，k为气体导热系数，W/(mm·K)；x为特征长度，mm；Re为雷诺数；Pr为普朗特数。

轴承内部结构比较复杂，当轴承高速运转时，其内部流体的流速和雷诺数很难准确计算，一般采用经验值估算。

在图3中，TA为压缩机内的介质温度，T0为通入轴承腔室的密封气温度，二者均为已知值。T2～T6为未知温度。根据广义欧姆定律，列出轴承的热传递模型，如式（4）所示。

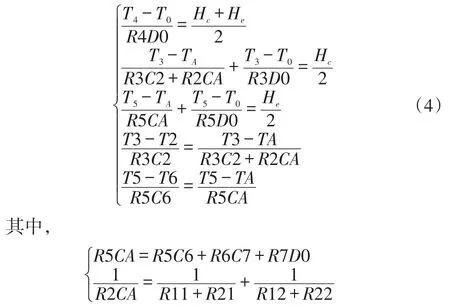
1.3 温度分布

某型低温压缩机的角接触轴承主要计算参数为：d=85mm，D=150mm，b=28mm，Db=18.5mm，Z=16，θ=15°，f0=1.5，v=25mm2/s，n=4 000r/min。分别计算常温运行和低温运行时轴承的温度分布情况，在低温工况计算时应在图3的热阻网格节点7处增加电加热功率320W，结果如表3所示。

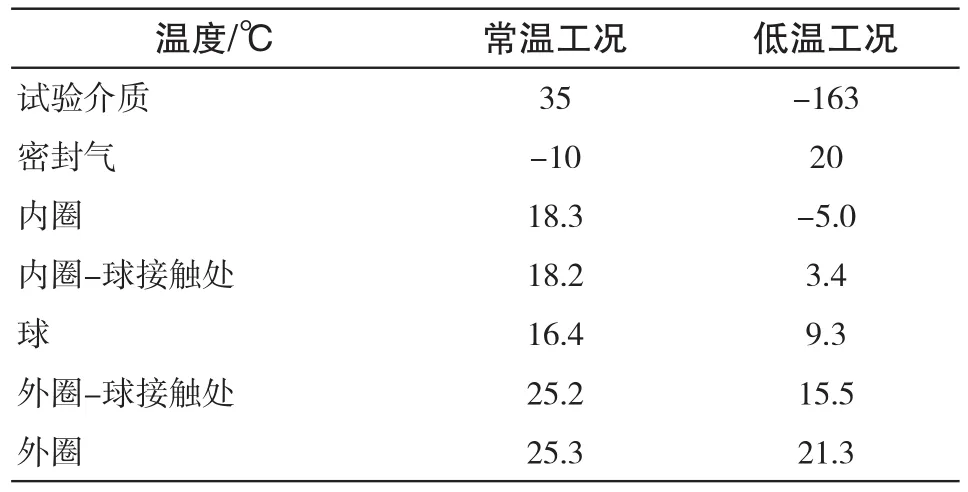
表3 轴承温度分布Tab.3 Distribution of bearing temperature

从计算结果可知，常温工况下由于钢球热阻较小，在密封气的强制冷却下温度较低，而外圈由于散热较差，温度最高。低温工况下轴承的温度主要靠电加热维持，从外圈至内圈逐渐减小。

2 试验数据及分析

某型压缩机在常温和低温工况运行时，分别记录推力轴承的温度、密封气温度、试验介质温度以及电加热功率等参数，由于温度传感器安装在轴承外圈表面，因此取轴承外圈的温度作为研究对象。

常温运行工况下，当试验介质温度和密封气温度分别为35℃和-10℃时，轴承外圈温度的计算值和实验值均随着转速的升高呈现加快上升的趋势，当转速为6 400r/min时轴承外圈实际温度达到41.2℃。常温运行的试验数据如图4所示。

图4 常温工况轴承外圈温度Fig.4 Bearing outer ring temperature in normal temperature condition

低温运行工况下，当试验介质温度和密封气温度分别为-163℃和20℃时，计算结果表明：如果没有电加热辅助措施，轴承外圈温度将低于-60℃，此时轴承油脂将无法正常工作。此时轴承自身发热不足以维持合适的温度，需要借助安装在轴承座表面的电加热装置来给轴承保温。设置电加热功率为350W，轴承外圈温度可保持在常温范围内，随着转速的上升，轴承外圈温度也随之缓慢升高，规律和常温试验类似。低温运行的试验数据如图5所示。

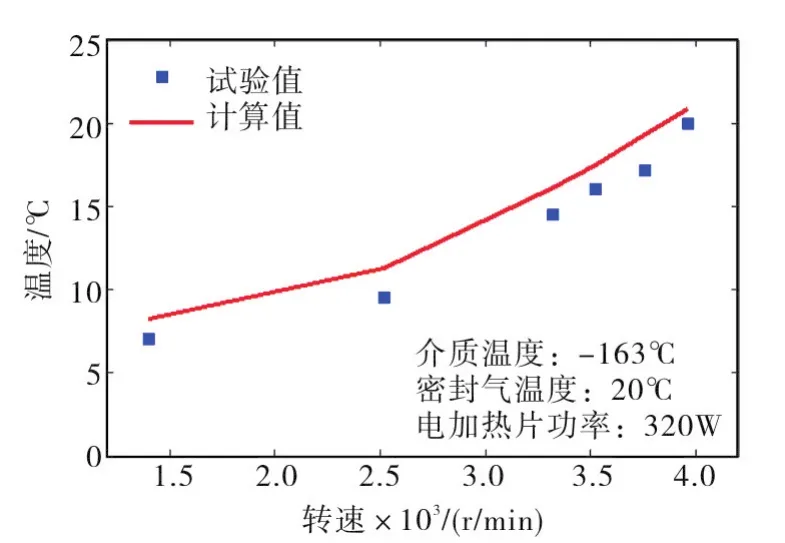
图5 低温工况轴承外圈温度Fig.5 Bearing outer ring temperature in low-temperature condition

对比常温和低温试验数据还可以发现：轴承外圈温度的实验值比理论计算值低2～5℃，这是因为理论计算的温度值为稳态传热结果，而在实验过程中，压缩机在每个转速的运行时间较短，记录的轴承外圈温度还未完全达到稳定状态。此外，对流换热系数计算和摩擦系数的取值也有一定的误差。

目前的试验仅获取了轴承外圈的温度数据，下一步将借助无线技术[19]测量轴承滚珠及内圈的温度，进一步精确分析轴承的传热特性。

3 结论

1）建立的轴承生热参数化模型考虑到了轴承的润滑、负载、传热等因素，具有较强的适用性，与实验数据具有较高的吻合度，误差约10%。

2）采用脂润滑的高速滚动轴承具有发热大、散热差的特点，在实际运行过程中应特别注重轴承的散热设计。

3）采取的低温密封气体强制冷却和电加热联合控温方案可以有效地将轴承温度保持在合理范围之内。