关于三角代数上的广义Engel条件

(1.沈阳航空航天大学 理学院，辽宁 沈阳 110037;2.大庆市第二十八中学，黑龙江 大庆 163000;3.吉林大学 数学学院，吉林 长春 130012)

1 引言

设R是有单位元的交换环，A，B是R上的酉代数，M是一个非零(A，B)-酉双模，则形式矩阵的集合

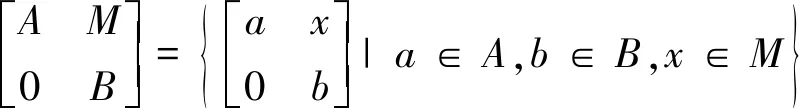
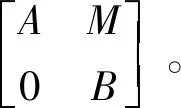
近些年来，关于环上的Engel条件问题越来越引起人们的注意，很多学者进一步讨论了素环以及非零素环上的Engel条件，如：Lanski[5]将文献[6]中所讨论的条件推广到Engel条件[…[[d(x)，x]，x]，…，x]=[d(x)，x]k=0 (其中k是大于1的正整数)，证明了若素环R的导子d在R一个非零理想上满足Engel条件，则R是交换环。 文献[7]证明了若特征非2的素环R上有非零导子d1，d2,…，dn满足[[…[d1(U1)，d2(U2)]，…]，dn(Un)]⊆Z(其中Z是R的中心)，U1，U2，…，Un是R的Lie理想，则存在i∈{1，2，…，n}，使得Ui⊆Z。 文献[8]研究了更一般的Engel条件[d(x)n(x)，xn(x)]k=0，n(x)≥1，证明了若非零素环R不含非零的诣零理想，且有导子d满足Engel条件，则d=0。文献[9]证明了若L是半素环R的非零左理想，d是半素环R的非零导子，且满足[[[d(xt0)，xt1]，…]，xtn]=0，任意的x∈L，其中t0，t1，…，tn都是正整数，则d(L)与d(R)L生成的理想含于中心，或者d(L)=0。关于三角代数和导子的研究，文献[10]给出了T满足[D(x)，D(Y)]=0的导子的结构。文献[11-12]给出了三角代数上Lie理想的高阶导子的结构。后几篇文献只讨论了三角代数导子的结构。

由于三角代数不再是普通环结构，而是矩阵形式，很多素环上的结果不再成立。本文给出了三角代数上满足Engel条件：①[[…[[D(Xm)，Xn1]，Xn2]，…]，Xnk]=0；②[[…[[D(Xm)Xn-XpG(Xq)，Xn1]，Xn2]，…]，Xnk]=0之一的导子的结构，其中m，n，p，q，n1，n2，…，nk是任意的正整数。文中，还给出了几种三角代数上导子为0的Engel条件。

2 主要结果

(1)

且对任意a∈A，b∈B，x∈M，有

f(ax)=dA(a)x+af(x)，f(xb)=f(x)b+xdB(b)，h(ax)=gA(a)x+ah(x)，h(xb)=h(x)b+xgB(b)。

(2)

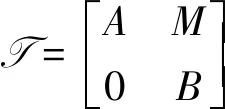
证明:设D是T上的导子且形如式(1)，其中f=0。 由式(2)可知： 对任意a∈A，b∈B，x∈M，有dA(a)x=0，xdB(b)=0。又因为M是忠实的，故dA=0，dB=0。

记[x，y]1=[x，y]，记[x，y]k=[[x，y]，y]k-1，其中k是大于1的正整数。

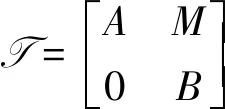
证明:设D，G是T的导子，形如式(1)，且任意X∈T都满足广义Engel条件。

[[…[[D(Xm)Xn-XpG(Xq)，Xn1]，Xn2]，…]，Xnk]=0。

(3)

于是由

知u=0。

于是由

得v=0。

从而

于是由

可知任意x∈M，都有f(x)=0。由引理2.1知，dA(A)=0，dB(B)=0，因此D=0。

故

于是，对任意x∈M，都有h(x)=0。由引理2.1知，gA(A)=0，gB(B)=0，因此G=0。

利用定理2.1,容易得到以下推论。

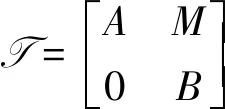
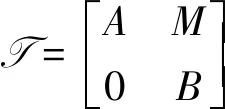
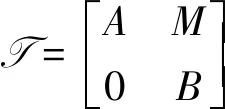
经过直接计算，得到下面非常有用的引理。

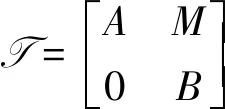
其中

且

E0=cx-xd，Ei=[c，a]ix-x[d，b]i，i≥1。

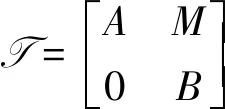
Z(T)={a⊕b|ax=xb，x∈M}。

利用以上引理2.3可证：

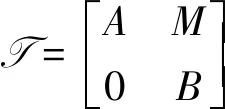
证明:设D，G是T的导子，形如(1)式，且对任意X∈T满足广义Engel条件[D(X)，X]kX-X[G(X)，X]k=0。由引理2.2，有

对任意a∈A，b∈B，x∈M都成立，其中

且

D0=dA(a)x-xdB(b)，Di=[dA(a)，a]ix-x[dB(b)，b]i，i≥1。

经过直接计算，可得

其中

0=Δ=[dA(a)，a]kx-x[gB(b)，b]k+(Δ(D)k)b-a(Δ(G)k)，

且

G0=gA(a)x-xgB(b)，Gi=[gA(a)，a]ix-x[gB(b)，b]i，i≥1，

即

(4)

式(4)中，分别取a=0，b=1，x=0和a=1，b=0，x=0，可得u=0，v=0。因此式(4)可化简为

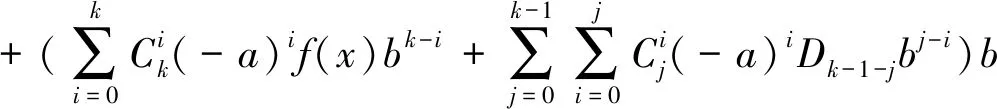
(5)

式(5)中取a=0，b=1。由于dA(0)=gA(0)=0，dB(1)=gB(1)=0，此时Di=Gi=0。因此，式(5)可化简为f(x)=0对任意x∈M。 由引理2.3知dA=0，dB=0，从而D=0且式(5)可化简为

(6)

式(6)中，取a=1，b=0由于gA(1)=0，gB(0)=0，此时Gi=0。因此式(6)可以化简为h(x)=0对任意x∈M。由引理2.3知，gA=0，gB=0。因此G=0。

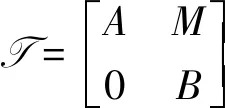
3 结论

以三角代数为背景，给出了三角代数上满足一定Engel条件的导子的结构，并由三角代数矩阵形式，得到了一些三角代数上导子为0的Engel条件。该研究思路可为广义二阶矩阵环或上三角矩阵环上的导子Engel条件的讨论提供一定参考。