基于刷扫和研磨的复合式小行星取样器取样过程仿真与分析
董成成,张 军,陆 希,黄 帆,倪江生,黄繁章,江朝军
(1.东南大学 仪器科学与工程学院,江苏 南京 210000;2.上海卫星工程研究所,上海 201109)
0 引言
随着航天科学技术的发展,人类对太空的探索能力不断增强,除了对月球和火星的探测外,对小行星的探测已经成为了现代深空探测的重要内容之一。小行星探测具有重要的意义,可解答星球起源、外星生命存在的问题,探索外空资源,为人类利用空间资源和能源提供技术支撑[1]。小行星表面重力加速度小,地质状况复杂,没有大气,所以在小行星表面取样必须克服两大困难:1)取样器必须能在微重力环境正常工作;2)取样器必须轻巧,能够工作在复杂未知的物理环境中[1]。
传统的行星取样器一般采用投射撞击[2]、钻头钻取[3]、气体吹取[4]、刷轮刷扫[5,8]的方法取样。2003年,日本发射的“隼鸟号”探测器,向小行星表面发射一颗直径约为1 cm、质量为10 g,速度为300 m/s的射弹撞击小行星,强大的冲击力使小行星表面的岩石破碎溅起[1-2],然后再对样品进行收集。这种取样方法新颖,但是收集的样品质量相对较小,无法满足科学研究。Bar-cohen等[6]设计了超声波钻孔取样器,通过钻头钻进小行星表面,实现对样品的收集。该方法取样时钻头与孔壁之间会产生很大的摩擦热能,小行星表面没有大气,热量难以消散,需要有效的冷却系统。美国国家航空航天局(NASA)发射的“奥西里斯-雷克斯”探测器,利用气体吹袭小行星表面使样品颗粒飞溅,然后再对溅起的物质进行采集[4]。使用气体吹取的取样方式能有效对小行星表面的颗粒进行取样,但是对小行星表面岩石和深层取样时效率会降低。同时,取样器结构会比较复杂,成本较高。欧洲航天局(ESA)发起的Phobos 小行星样品收集返回任务[7],提出了一种基于刷扫取样的方法。取样器在接触小行星表面时,通过刷轮对小行星表面颗粒进行刷扫,将样品颗粒收集到容器中。该取样器结构简单,取样与收集一体化,但根据Christoph等[8]对行星风化层表面取样的仿真结果可知,当风化层凝聚力较大时,颗粒之间会比较紧固,采用刷轮直接刷扫,颗粒不容易直接被刷扫到样品容器中,在复杂的取样环境中取样效率会降低。
为了克服小行星表面取样时机械属性未知的困难,设计了一种基于刷扫和研磨的复合式取样器。在小行星表面星壤颗粒间凝聚力较大或者遇到岩石取样时,取样器的研磨机构对样品研磨搅动形成松散的颗粒,刷扫机构再对颗粒刷扫取样。刷扫和研磨的复合取样方式能够提高取样器取样的效率,并适用于复杂的取样环境中,提高整个小行星取样器取样探测任务成功的概率。为了验证所提出的复合式小行星取样器设计方案的可行性,本文基于离散元仿真软件EDEM 对取样过程进行仿真与分析。文章首先介绍了小行星取样器的模型及工作原理;其次进行了样品颗粒相互作用建模,以及研磨取样的动力学过程分析;最后在此基础开展了仿真实验和结果分析。
1 小行星取样器的模型介绍
取样器的整体示意图如图1 所示。取样器主要由刷扫机构、研磨机构、样品容器组成。
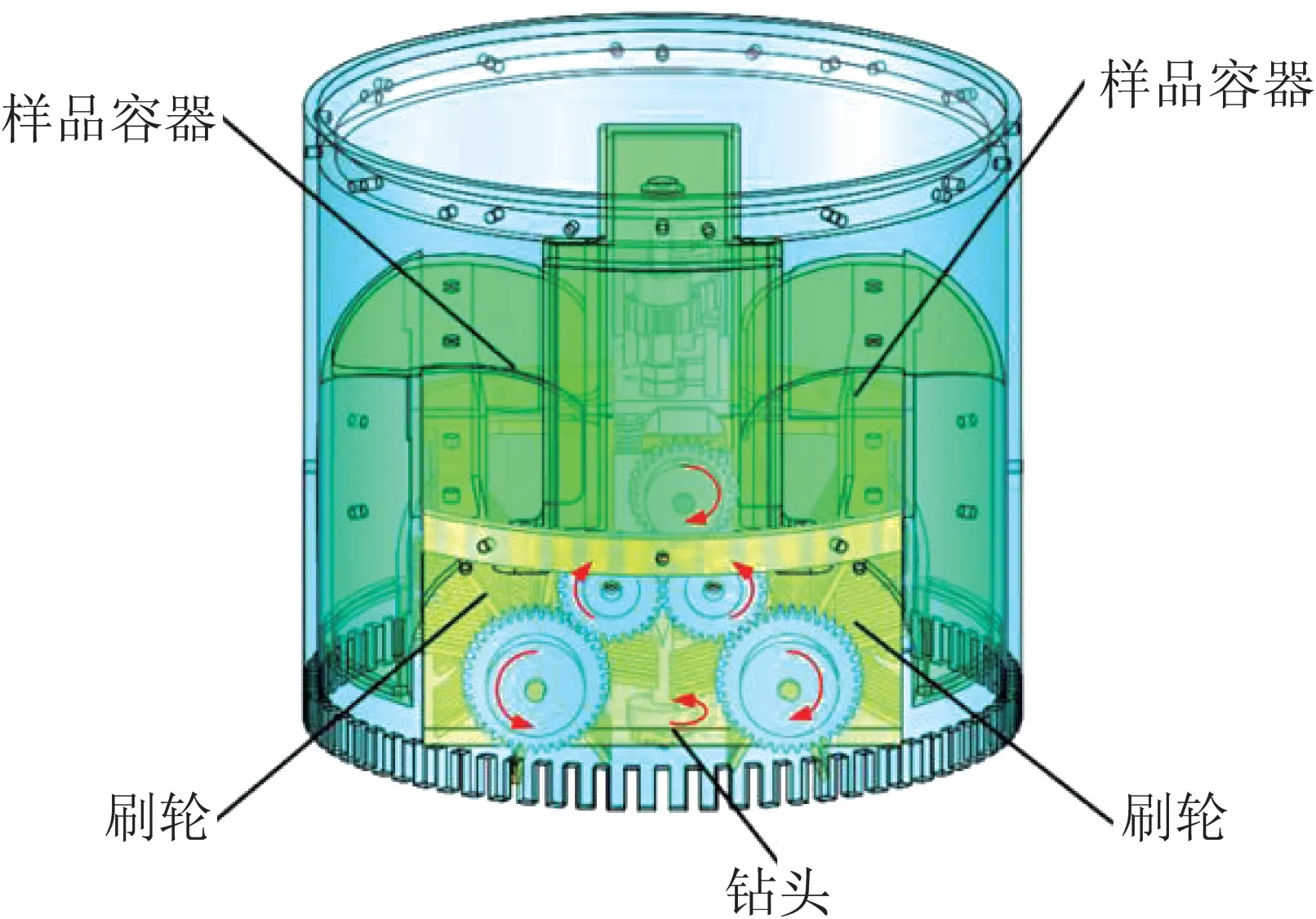
图1 取样器整体示意图Fig.1 General diagram of the sampler
在小行星表面取样时,取样器通过感知取样地点的样品机械属性制定工作模式。当取样地点的样品颗粒比较松散,刷扫机构单独工作对颗粒刷扫。由电机驱动刷轮转动,从面向取样器正视图看,左边的刷轮逆时针转动,右边的刷轮顺时针转动,将颗粒刷扫到两边的样品容器中。当取样地点的样品比较紧固,刷扫机构和研磨机构协同工作,研磨机构的钻头在电机的驱动下对样品进行打磨形成松散的样品颗粒,刷扫机构再对颗粒刷扫取样。该复合式小行星取样器,通过感知取样地点的环境信息情况,智能控制刷扫机构和研磨机构的工作,降低取样器取样时的系统功耗,同时也能适应小行表面复杂的取样环境,提高取样器的取样效率。
2 离散单元法计算模型的建立
离散元法是一种把颗粒划分为相互独立的对象进行研究的方法。根据颗粒间的接触模型和牛顿运动定律,利用迭代算法计算固定时间间隔内颗粒的受力与位移,然后更新全部颗粒的状态,求得颗粒体系的宏观运动特性。离散元法在处理颗粒体系内力的作用时应遵循瞬时平衡原则[9],所以离散元法的计算核心包含两个方面:1)接触模型,即力与形变的关系;2)牛顿第二定律,根据粒子的受力计算粒子的运动方程[10]。
2.1 颗粒间的接触模型
为准确描述样品颗粒接触的瞬态力学行为,本文采用EDEM 内置的计算结果准确、计算效率高、最常使用的Hertz-Mindlin 无滑动弹性接触模型。该接触模型属于硬颗粒接触模型,假定颗粒之间的碰撞是瞬时产生的,碰撞之后的颗粒相互分离,在颗粒表面承受的应力低时,颗粒之间不发生显著的塑性变形,适用于离散颗粒流的相互接触。小行星表面的样品颗粒是坚硬的岩石颗粒,发生碰撞后样品颗粒不会相互黏结,取样器对样品进行取样时的作用力不会让样品颗粒发生变形,颗粒的运动状态满足Hertz-Mindlin 无滑动弹性接触模型的应用条件。同时,该接触模型计算效率和准确性高,使用该颗粒接触模型能够准确描述取样器在小行星表层取样时离散样品颗粒间的相互作用。该模型中粒子的法向力和切向力都有阻尼分量,并且与阻尼系数和恢复系数有关。切向摩擦遵循库伦摩擦定律,滚动摩擦通过接触独立定向恒转矩模型(Con⁃tact Independent Directional Constant Torque Mod⁃el)实现。粒子碰撞接触模型[9-10]原理如图2 所示。
设两弹性接触颗粒半径分别为RA与RB,法向量重叠为δn,则

图2 Hertz-Mindlin 无滑动弹性接触模型[9-10]Fig.2 Hertz-Mindlin non-slip elastic contact model[9-10]

式中:rA和rB为圆球形颗粒的位置矢量。
设颗粒接触半径为

式中:R*为颗粒的等效半径。
R*与接触颗粒半径RA、RB的关系为

粒子发生碰撞时颗粒接触法向力Fnormal为a的函数:

式中:E*为等效弹性模量,

其中,EA、vA、EB、vB分别为颗粒A 和颗粒B 的弹性模量和泊松比。

式中:m*为等效质量,其值为

用vA、vB表示颗粒碰撞前的速度,n表示碰撞时的法向单位矢量,则

为相对速度在法向上的投影,

其中,阻尼系数β与法向刚度kn分别为

式中:e为恢复系数。
颗粒间的切向力Ftangential为

式中:δt为切向重叠量;kt为切向刚度。

式中:G*为等效剪切模量,其值为
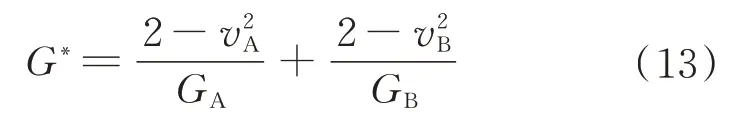
其中,GA、GB为两颗粒的剪切模量。
颗粒间的切向阻尼力为

2.2 离散元法的颗粒模型运动方程
Hertz-Mindlin 无滑动弹性接触模型描述了离散元颗粒的相互作用,而离散元颗粒运动的位移则根据牛顿第二定律计算得出[9-10]。根据瞬时平衡原则,颗粒i的运动方程为

利用中心差分法对上面两式进行数值积分,得到以两次迭代时间步长的中间点表示的速度为

再对式(16)进行积分,可得到关于位移的等式为

根据式(17)得到更新之后的位移,再将其带入接触模型求得对应的接触力,经过不断地迭代更新,可得任意时间点颗粒的运动,实现跟踪了每个颗粒在任何时候的运动轨迹,计算流程如图3 所示。
2.3 研磨过程的动力学分析

图3 离散元法计算流程Fig.3 Calculation process of the discrete element method
本文要通过仿真研究研磨对取样器取样效率的影响,而样品的物理属性、研磨机构的机械属性以及推进速度等因素都会影响研磨机构对样品颗粒的作用,所以根据特定的取样环境合理地设置仿真参数是仿真成功的关键。基于上述颗粒接触模型,对研磨过程进行动力学分析,分析研磨机构与粒子接触时的作用力与上述因素之间的关系,为合理设置研磨机构的仿真参数和分析研磨效果提供理论依据。
研磨是研磨机构钻头的切片对小行星表面的星壤切开并分离的过程,研磨从运动过程上分析可分为两个过程——钻头对星壤的压入和切片对星壤的切削。简化分析过程,对这两个过程进行独立分析。
2.3.1 压入过程的动力学解析
在静力加载下,钻头压入风化层内部,模型示意图如图4(a)所示;钻头底部的切片与星壤接触,单独对每个切片分析,模型示意图如4(b)所示。
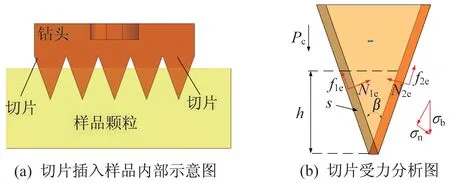
图4 钻头与样品接触示意图Fig.4 Contact diagram of the drill bit and the sample
图4中,切片所受的压力为Pc,切片的切削尖角为β,切片宽度为l,压入深度为h,切片与星壤的接触面积为S,星壤的抗剪强度为σb,切片法向的抗剪强度为σn,定义f1e和f2e分别为切片壁板刃面摩擦力,N1e和N2e分别为切片壁板刃面法向力,对每个切片受力分析有
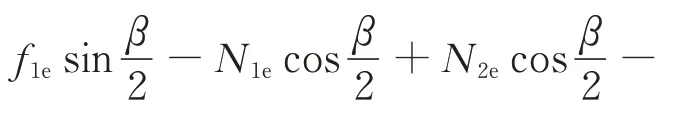

切片刃面切向力与法向力的对应关系式如下(其中μ为切片与星壤间的摩擦系数):

根据土壤切削理论,切片刃面法向力的表达式为

式中:σn和S的计算公式为
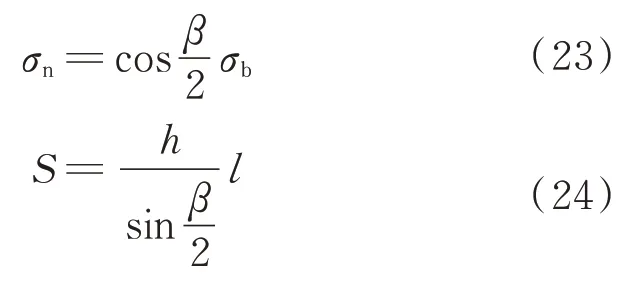
其中,星壤的抗剪强度σb的表达式为
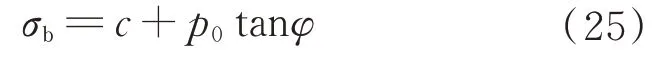
式中:c为星壤的凝聚力;p0为星壤表面法向压力;φ为星壤表面颗粒的内摩擦角。
每个切片受到的正压力Pc的表达式为

2.3.2 切削过程的动力学解析
切片的回转切削是指切片在水平力矩的作用下破坏星壤的内部结构,导致星壤发生形变或者断裂,最后被切片刃面剪碎成粉末状的过程。切片对星壤切削深度为h,切片与星壤的接触模型如图5 所示,绕轴旋转切削后星壤内部形成圆台孔。为简化分析过程,对每个切片进行分析,分析旋转切削过程中切片对星壤的水平切削合力。
切片切入深度为h,切片与星壤表面的接触半径为a,即

式中:A为切片侧面的宽度;H为切片的高度。
用η来表示切片侧面的宽度与高度之比,即

插入深度为h后,切片切削星壤的质量为m,ρ为星壤的密度,则m的表达式为

图5 切片切削星壤示意图Fig.5 Schematic diagram of the cutter cutting the regolith


切片的动量矩L为

式中:w为切片的角加速度;n为切片的转速。
对单次切削过程的首末端应用动量矩定理,得

式中:FM为切削合力;dM为合力矩;t为切削时间;v为切片向下推进速度。
FM的表达式为

从上述模型分析中可得出钻头压入星壤内部的静压力与星壤的凝聚力和插入深度成正比,切片对星壤的切削合力与取样器的下降速度和切片的转速成正比。在不影响取样器正常工作的情况下,适当地增大钻头的转速和取样器的下降速度有利于增强研磨机构对星壤的研磨效果。
3 取样器取样过程EDEM 仿真
3.1 仿真参数设置
EDEM 软件仿真由3 个模块构成:前处理器、求解器和后处理。前处理用于创建和初始化离散元模型,设置相应模型和参数,包括颗粒与取样器的材料属性,颗粒之间、颗粒与取样器之间的接触属性,颗粒参数属性。
1)查阅相关资料得知,“丝川”小行星表面的岩石密度为3.2 g/cm3,小行星整体密度为1.9 g/cm3,可以近似估算小行星表面样品颗粒的平均密度为2.5 g/cm3,故本次仿真中选取的样品颗粒为等密度的岩石颗粒。由于钢的硬度高,变形小,使用钢性材质的刷轮和钻头能够提高取样器刷扫和研磨的效果,仿真实验中取样器材质设置为钢,查阅相关物理手册设置颗粒与取样器的材料属性见表1。

表1 颗粒与取样器的材料属性Tab.1 Material properties of the particles and the sampler
2)颗粒和取样器发生碰撞时两者的碰撞恢复系数、静摩擦系数和滚动摩擦系数与发生接触物体的物理属性相关,不同状态下碰撞物体之间的接触参数需要通过实验测定或者通过“虚拟实验”标定。本次仿真中样品颗粒与取样器之间的接触属性参数设置参照正常状态下岩石和钢之间的碰撞接触参数,具体参数设置见表2。
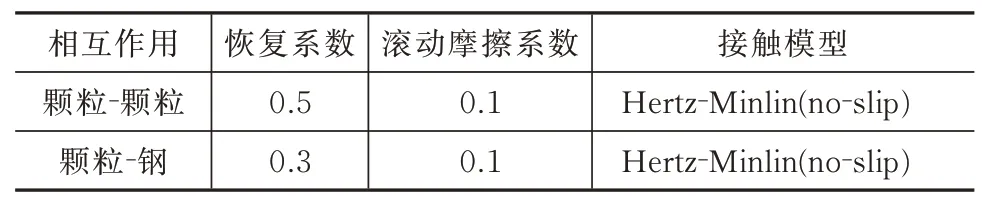
表2 颗粒之间、颗粒与取样器之间的接触属性Tab.2 Contact properties among the particles and the sampler
3)仿真模型设置颗粒直径为1.5 mm,形状为圆球形,生成的颗粒形状如图6 所示。设置粒子工厂类型为Dynamic,产生区域为取样器正下方的矩形区域,颗粒总数为40 000,颗粒生成后,取样器正好与颗粒的上表面接触。

图6 颗粒仿真模型Fig.6 Simulation model of a particle
4)研究取样器刷轮的叶片数、转速和推进速度、星壤参数属性以及研磨机构的作用对取样效率的影响,设置不同的参数进行仿真实验,基于离散元仿真软件EDEM 设置仿真参数见表3。
3.2 仿真过程描述
图7(a)为仿真前模型示意图,取样器的正下方是一个长方体区域,动态生成的颗粒随机遍布在该区域,取样器刷扫机构刷轮的叶片与颗粒的上表面接触。开始仿真刷扫取样后,取样器整体以一定的推进速度向下运动,同时刷扫机构的左刷轮以一定转速逆时针转动,右刷轮顺时针转动。随着取样器的不断向下推进,刷轮对颗粒进行刷扫,颗粒沿着样品容器的导轨进入到样品容器中。图7(b)为仿真4 s 后模型示意图,取样器的样品容器中已经充满了粒子。研磨机构的作用图如图8 所示,研磨机构的钻头对颗粒整体进行研磨,使其周围颗粒松散,在微重力环境下,部分颗粒会悬浮在空中。

图7 刷扫前后的模型示意图Fig.7 Schematic diagram of the model before and after brushing

图8 研磨前后的模型示意图Fig.8 Schematic diagram of the model before and after grinding
3.3 仿真结果分析
取样器刷轮叶片数、刷轮转速,取样器向下推进速度对取样器取样质量影响的仿真结果如图9 所示。8 片叶片的刷轮,相同的取样时间下,取样质量高于6 片、4 片叶片的刷轮,表明刷扫机构刷轮叶片越多,能够刷扫的样品越多(见图9(a))。在不考虑刷轮力矩对取样器取样工作的影响,刷轮的转速越大,取样器向下的推进速度越快,取样器采集的样品越多(见图9(b)和图9(c))。
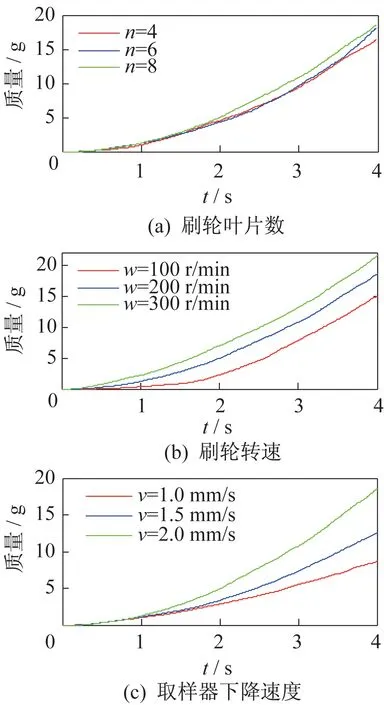
图9 取样质量与取样器参数关系的仿真结果Fig .9 Simulation results of the relationships of the sampling qualities and the sampler parameters
小行星表面星壤内摩擦角和凝聚力对取样效率影响的仿真结果如图10 所示。改变星壤的内摩擦角,对取样器取样质量的影响很小,而改变星壤内部的凝聚力,取样器取样质量有明显的变化(见图10(a)),表明星壤凝聚力是星壤影响取样器取样效率的主要因素(见图10(b))。当星壤内部凝聚力为10 kPa 时,相同的取样时间,取样器采集的样品最多,增大星壤的凝聚力,取样质量反而降低。结果表明:星壤内部凝聚力在10 kPa 左右时,取样器取样效率最高;然后随着凝聚力的增大,取样器取样效率会降低。
取样器在不同凝聚力的星壤表面取样时,研磨对取样质量的影响结果如图11 所示。当星壤内部没有凝聚力或者凝聚力很小时,星壤颗粒间比较松散,刷轮能够直接对颗粒刷扫,研磨机构的作用对取样器取样质量的影响很小(见图11(a)和图11(b))。当星壤粒子间凝聚力为20 kPa 时,研磨机构的作用使取样质量增加8 g 左右,增大星壤内部凝聚力为50 kPa,研磨机构的作用对取样质量的增加幅度降低,对取样器取样质量增加约2 g 左右(见图11(a)和图11(b))。实验结果表明:在星壤内部凝聚力为20 kPa 左右时,研磨能够显著提高取样器取样效率;随着凝聚力的增大,研磨机构压入样品内部的静压力增大,阻力消耗的功率增大,切削合力消耗的功率减小,研磨机构对取样效率的提高幅度会降低。

图10 取样质量与星壤参数关系的仿真结果Fig.10 Simulation results of the relationships of the sampling qualities and the sample parameters

图11 研磨对取样质量影响的仿真结果Fig.11 Simulation results of the effects of grinding on the sampling quality
图12 和图13 分别表示刷轮和研磨机构以转速为100 r/min 工作时,不同凝聚力下,轴向力矩的变化图。如图12 所示:刷轮刚接触星壤表面时,星壤凝聚力越大,刷轮的力矩就越大;随着取样器向下推进,刷轮慢慢的刷进星壤内部,刷轮的力矩呈现周期性的变化,其频率与刷轮的频率相同。如图13所示:当星壤内部凝聚力很小时,研磨机构研磨时的力矩很小;随着星壤凝聚力的增大,取样器的不断向下推进,研磨机构研磨星壤的力矩逐渐增大。

图12 刷轮刷扫样品时轴向转矩变化图Fig.12 Change diagram of the axial torque of the brush wheel when brushing samples

图13 研磨机构研磨样品时轴向转矩变化图Fig.13 Change diagram of the axial torque of the grinding mechanism when grinding samples
从图13 可以得出:刷轮在刚开始接触星壤表面时,随着样品间凝聚力的增大,力矩会迅速增大;随着刷轮刷扫到星壤内部,微重力环境下,刷轮在每个周期内刷扫样品的力矩变化很小。所以取样器在凝聚力较大的星壤表面取样时,刷轮在接触星壤表面的瞬间容易发生堵转,取样器在要接触星壤的表面时,向下的推进速度要尽量减小。由于小行星表面重力加速度很小,研磨机构研磨样品会造成样品离开小行星表面,从图13 可以看出:研磨机构工作的力矩远小于刷轮工作的力矩;随着研磨深度的增加,工作力矩会随之增加,所以为了减小取样器的系统功耗,驱动研磨机构的电机功率可以适当减小。
4 结束语
本文基于刷扫取样方法,提出了一种基于刷扫和研磨的复合式小行星取样器。基于离散元软件EDEM,仿真分析了取样器参数、星壤参数对取样器取样质量的影响,并验证了基于刷扫和研磨的复合取样方式能够提高取样器的取样效率,同时仿真不同凝聚力下刷轮和研磨机构工作时的驱动力矩。但本文在分析取样器参数、星壤参数和研磨机构的作用对取样效率影响时,未考虑星壤表面颗粒的大小或形状对仿真结果的影响,以后要完善对小行星表面星壤的模拟。同时本文只是考虑研磨机构对样品颗粒的研磨,后面要考虑研磨机构对大块颗粒或者岩石进行研磨,并且通过实验来验证仿真的准确性。

