柔索并联式导弹自动抓取装置动力学仿真
唐文献,杨珺柳,李佳圣,解 强,彭永红
(1.江苏科技大学 机械工程学院,江苏 镇江 212000;2.上海机电工程研究所,上海 201109)
0 引言
导弹全自动装填[1]逐步成为防空导弹装填车未来发展的关键技术[2]。抓取装置作为导弹自动装填系统的关键部件,用于导弹模块自动对准、抓取和对位下放。由于导弹自动装填所处的实际作业环境复杂,抓取装置相对导弹模块的位姿产生随机变化。如果抓取装置为全刚性结构,则需要抓取装置相对导弹模块的位姿始终能调整并保持在一个较高的精度范围内。为降低精度并提高抓取装置对位准确度,抓取装置可采用浮动对位原理和柔索并联式结构[3],以一段钢丝绳作为刚柔转换环节,利用钢丝绳的垂向伸收、径向挠变以补偿其与导弹模块之间的相对位置偏差。由于钢丝绳往往同时存在着弯曲、缠绕、拉直等多种状态,对采用钢丝绳柔性浮动对位原理的导弹自动装填抓取装置进行动力学建模和动态特性分析时,必须充分考虑钢丝绳柔性对动力学特性的影响。
钢丝绳建模在动力学研究上的难点在于绳子内部之间有摩擦力的存在以及阻尼系数和刚度系数难以确定。柔索动力学初期的研究主要集中在理论分析方面[4],比如基于连续介质力学理论进行绳线动力学建模[5]。但该类模型没有充分考虑迟滞阻尼、绳索内部摩擦等非线性动力学特性,且这类方法偏于理论分析,不适于实际工程应用。目前工程上大多数采用离散元的方法进行逼近,如瑞利-里兹(Reyliegh-Ritz)法、有限单元法和模态分析及综合法[6]。其中,基于伪刚体理论的有限段离散化方法[7]进行绳线动力学建模,考虑了质量、弯曲刚度、绳线转动的动力学特性。通过将钢丝绳离散为外形及质量均与相同尺寸的绳线结构一致的若干段刚性杆,各刚性杆之间通过弹簧阻尼连接,可模拟钢丝绳的拉伸、剪切、弯曲、扭转等各方向变形[8]。
本文以某导弹自动装填系统的抓取装置为研究对象,采用有限段离散化方法,基于ADAMS 软件以及宏命令对抓取装置上钢丝绳柔性建模。考虑钢丝绳柔性以及抓取装置与导弹模块结构非线性碰撞的耦合影响,仿真分析抓取装置钢丝绳柔性和结构接触耦合作用下,抓取装置下放-抓弹-吊弹过程中的运动和受力特性的动力学特性,验证柔索并联式抓取装置对对位姿态偏差的自适应调整能力,为导弹自动装填系统设计提供参考。
1 导弹自动装填抓取装置
1.1 抓取装置结构与刚柔转换原理
抓取装置结构主要由上层本体和下层本体构成,两层本体之间通过钢丝绳相连。抓取装置结构和坐标系定义如图1 所示。抓取装置下方装有4 个吊钩,与导弹模块上方的4 个吊耳相配合,从而实现抓取动作。为了减小抓取的难度,吊钩上接触面设置为斜角型,下接触面设置为平面型。
通过在抓取装置上、下层本体之间设定一个钢丝绳柔性环节,在抓弹和放弹动作之前下放钢丝绳,实现抓取装置的刚、柔性转换,便可利用钢丝绳柔性与结构导向斜面共同作用,实现抓取装置相对导弹模块位姿的自适应调整。
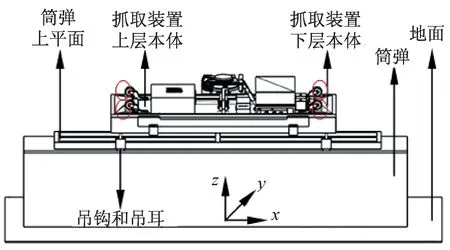
图1 抓取装置示意图Fig.1 Schematic diagram of the gripping device
1.2 工作流程
导弹自动抓取装置吊取导弹模块的动作包括抓取装置下放-抓弹-吊弹过程。具体工作流程图如图2 所示。

图2 工作流程图Fig.2 Work flow chart
1.3 极限工况
抓取流程执行前的初始状态要求抓取装置平行于导弹模块。考虑到装填抓取装置相对导弹模块安放面之间存在相对姿态调整误差,抓取装置与导弹模块之间的姿态关系可分为4 种工况见表1:完全对准调平、水平对准误差引起的导弹模块绕y轴和绕x轴的相对倾斜(俯仰角、横滚角)、方位对准误差引起的绕z轴方位角偏转。
其中工况1为理想工况,后3 种工况为抓取装置工作中的实际存在工况,其形式如图3 所示。

表1 抓取装置极限偏差Tab.1 Limit deviations of the gripping device
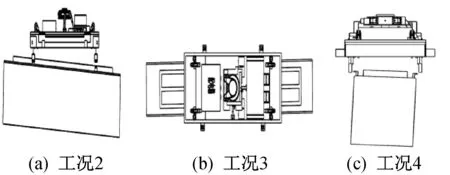
图3 抓取装置极限工况分析Fig.3 Analyses of the limit working conditions of the gripping device
2 抓取装置多体动力学建模
相比于钢丝绳引起的柔性特性,抓取装置的结构弹性变形相对较小,可以忽略。因此,在进行抓取装置动力学建模时,可以将抓取装置除去钢丝绳之外的结构部件作为多刚体模型,根据抓取装置各个部件的实际相对运动情况定义相互之间的相对运动关系,并设定接触约束参数,各个部件同时协作时还应考虑耦合性和非线性[9]。
2.1 多体动力学建模理论
多刚体系统动力学方程[10]为

式中:M为系统广义质量矩阵;q为系统广义坐标向量;Φ为位置约束方程;Φq为位置坐标矩阵对q求偏导;为位置坐标矩阵进行转置后对q求偏导;Φt为位置坐标矩阵对t求偏导;Φqt为位置坐标矩阵先对q再对t求偏导;Φtt为位置坐标矩阵对t求二阶偏导;f为外力向量;λ为拉格朗日乘子;t为时间;v为速度右项;η为加速度右项。
2.2 抓取装置多体动力学建模
根据抓取装置上、下层本体结构,利用ADAMS软件分别对抓取装置各部件之间施加相应的运动和受力约束,并建立全参数化的动力学模型[11]。建立抓取装置多体动力学模型如图4 所示。
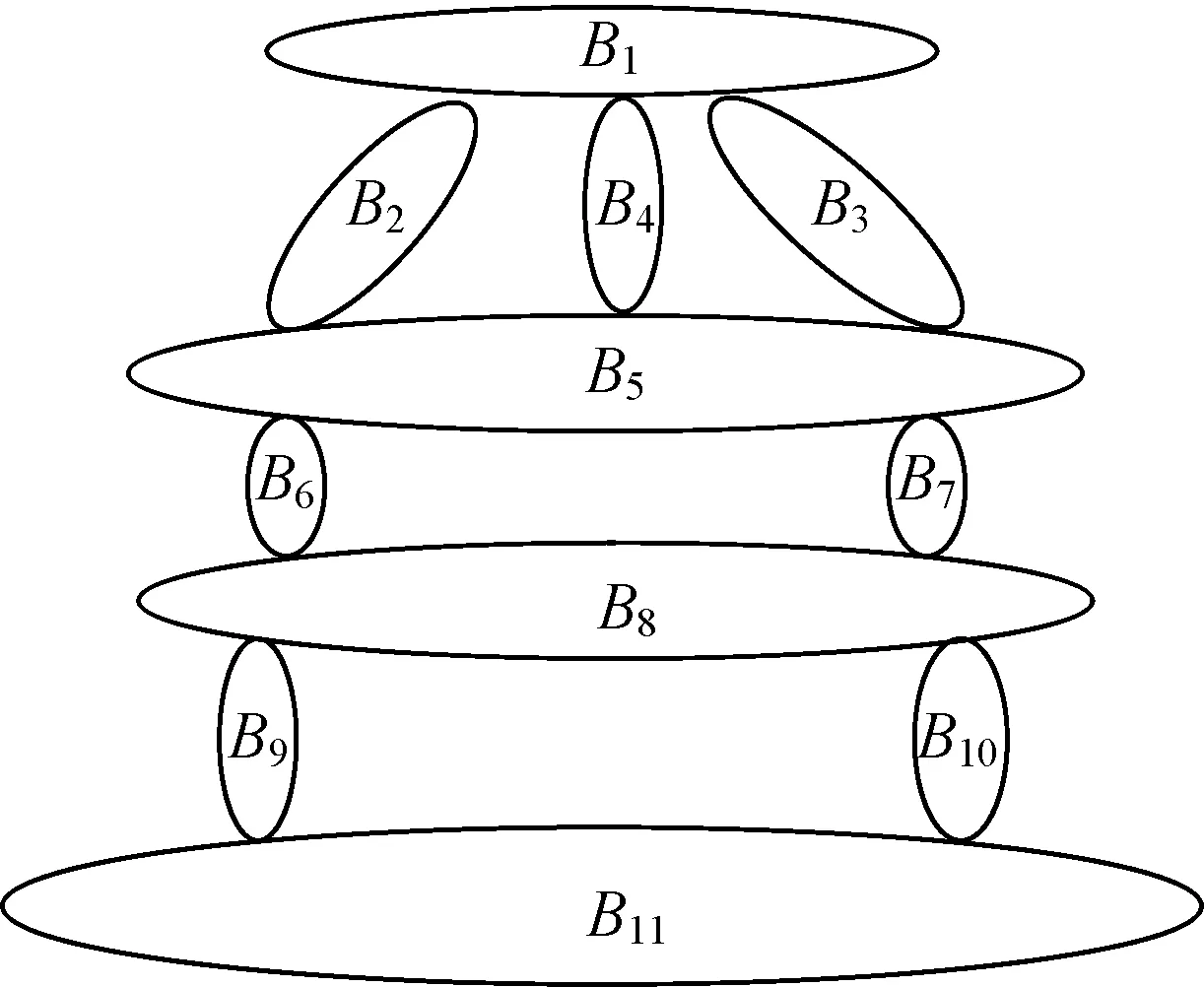
图4 抓取装置拓扑结构Fig.4 Topological structure of the gripping device
在图4中,B1为抓取装置上平台,B2为电动推杆1,B3为电动推杆2,B4为中间支承轴,B5为抓取装置上层本体,B6和B7为两侧钢丝绳,B8为抓取装置下层本体,B9和B10为吊钩,B11为导弹模块。B1和B2之间、B1和B3之间、B4和B5之间通过万向节连接,B1和B4之间固定连接,B2和B5之间、B3和B5之间以球铰连接,B5和B6固定连接,B5和B7固定连接,B6和B8固定连接,B7和B8固定连接。B9和B11定义为接触,B10和B11定义为接触,B11和地面定义为接触。
3 钢丝绳柔性建模
3.1 钢丝绳离散模型
基于有限段法将钢丝绳等效为多个以弹簧和阻尼器连接的刚性段,通过离散的刚性段表征绳线的惯性特征,以弹簧和阻尼器表征绳线的弹性和阻尼特征,离散后的钢丝绳可视为带有关节柔性的多刚体模型,如图5 所示。若采用球铰副连接则会忽略拉伸变形,对钢丝绳的抗弯、抗扭和抗拉刚度造成一定的失真现象[12]。故本文采用轴套力约束关系连接近似模拟钢丝绳离散段之间的相互关系。
通过定义3 个力分量{Fx,Fy,Fz}和3 个力矩分量{Tx,Ty,Tz}[13],在2 个钢丝绳离散段之间施加柔性力,构成一个6 分量的弹簧结构。作用力和作用力矩为
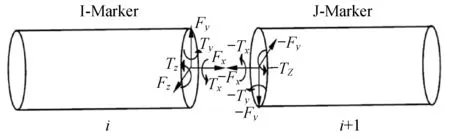
图5 钢丝绳离散段模型Fig.5 Discrete segment model for wirerope

式中:δi为第1个构件上的I-Marker坐标系相对于第2个构件上的J-Marker坐标系的相对位移;θi为I-Marker坐标系相对于J-Marker坐标系的相对位移;vi、ωi分别为IMarker坐标系相对于J-Marker坐标系的相对角位移;Fi0、Ti0分别是初始力载荷和力矩载荷。
钢丝绳离散段之间的拉伸和扭转刚度系数[14]为

式中:K11为拉伸刚度系数;K22、K33分别剪切刚度系数;K44为扭转刚度系数;K55、K66分别为弯曲刚度系数;E、G分别为钢丝绳的弹性模量和剪切模量;A、R、l分别为钢丝绳截面积、半径和钢丝绳每段长度;I为钢丝绳横截面对中性轴的惯性矩。
选用钢丝绳材料弹性模量E=2.0× 105MPa,泊松比为μ=0.25,剪切模量G=8.0× 104MPa[15],钢丝绳的型号为6×19,其结构参数见表2,计算得到刚度系数见表3。

表2 钢丝绳6×19 基本参数Tab.2 Basic parameters of the wirerope 6×19

表3 轴套力刚度系数Tab.3 Stiffness coefficient of the bushing force
3.2 钢丝绳离散段建模
当钢丝绳离散段无限小时,将与绳线连续体完全一致,但离散体数目的增多会使计算耗时大大增加。考虑到抓取装置的每根钢丝绳长度为95 mm,直径为12 mm,建模时将其离散成95 段(即每个离散段长度为1 mm)。其中一条钢丝绳编写的AD⁃AMS 宏命令如下:

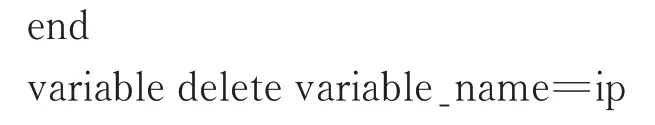
对上述编写的宏命令做4 次导入,建立抓取装置4 根钢丝绳离散模型。
钢丝绳的柔性、挠性以及刚度,在影响抓取装置运动性能的因素中,拉伸阻尼的影响很小,扭转阻尼系数对运动的影响不可忽视,设定刚性阻尼系数为1 N·s·mm−1,扭转阻尼系数为10 N·s·mm−1[13]。在钢丝绳离散段圆柱体之间施加轴套力约束。轴套力连接的刚性系数、阻尼系数、扭转系数以及扭转阻尼系数按表3中值设定。
采用轴套力约束将95 个离散段圆柱体连接起来,建立含柔性钢丝绳的抓取装置动力学模型,如图6 所示。
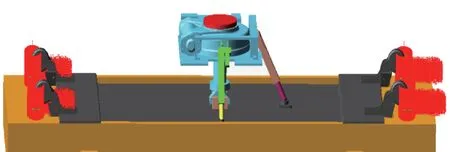
图6 含柔性钢丝绳的抓取装置动力学模型Fig.6 Dynamics model of the gripping device with flexible wirerope
4 抓取装置动力学仿真
4.1 仿真驱动流程
1)在0~2 s 内,以step 函数给整个抓取装置施加一个向下的平移驱动,使整个抓取装置下放100 mm。由于抓取装置距离导弹模块的距离为80 mm,所以抓取装置可完全贴合搁置在导弹模块上端平面,钢丝绳处于松弛状态。
2)在2~5 s 内,以step 函数给吊钩施加一个加紧方向上的速度驱动,使吊钩向导弹模块吊耳接近,吊钩的接触面在吊耳接触面的正下方移动,当吊钩的端面与吊耳的端面接触时吊钩运动停止。由此完成抓取装置对导弹模块的浮动对位和抓弹。
3)在5~8 s 内,以step 函数给抓取装置施加一个向上的位移驱动。随着抓取装置向上移动,钢丝绳逐渐张紧,吊钩与导弹模块吊耳接触从而提起导弹模块。
4.2 仿真与结果分析
按照1.3 节中的4 种工况设定抓取装置与导弹模块之间的初始相对位姿关系。对4 种工况下的抓弹与放弹过程仿真分析。在吊钩接触面上取中间点a1,吊耳上取中间点a2,两者在x、y、z方向上的相对距离即为抓取装置下放过程中与导弹模块之间的相对位移变化。
4.2.1 抓取装置-导弹模块接触力分析
抓取装置下放时,抓取装置与导弹模块的上层平面相接触。由于钢丝绳的柔性,不同姿态下导弹模块会在不同时间点与抓取装置发生不同形式的接触,接触力如图7 所示。
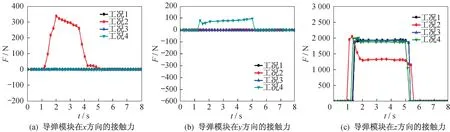
图7 抓取装置-导弹模块接触作用力曲线Fig.7 Contact force curves of the gripping device and the missile module
导弹模块在x方向的长度较长,当工况2中导弹模块绕y轴倾斜2.5°时,左右两端会出现较大的高度差。从图7中可以看出:这种高度差导致工况2中导弹模块高的一端先与抓取装置接触。起始接触时为线接触,接触力的方向竖直向上。2 s 以后抓取装置完全搁置在导弹模块上表面上时,接触力的方向垂直于导弹平面斜向上,接触力在x方向产生分量,z方向上的接触力减小。
工况3中当导弹模块绕z轴旋转0.7°时,导弹模块的上平面仍然处于水平状态,接触时间与接触形式与工况1 完全一致。
由于导弹模块在y方向上的宽度较小,工况4中导弹模块绕x轴倾斜2.5°时出现的高度差也较小,在1.2 s 左右抓取装置与导弹模块接触,2 s 后抓取装置完全搁置在导弹模块上表面之上,与导弹模块发生完全接触,接触力增大到与理想状态(即工况1)相等。同样,抓取装置与导弹模块完全接触时接触力的方向发生改变,z方向上的接触力减小。
4.2.2 抓取装置与导弹模块相对运动分析
2 s 以后,抓取装置上的吊钩开始夹紧动作,抓取装置与导弹模块在对位过程中,不同的导弹姿态将会引起抓取装置姿态的适应性改变,如图8(a)和图8(b)所示。5 s 以后,抓取装置提起导弹模块,钢丝绳先由松弛处于拉伸状态,接着吊钩的底面与导弹模块发生接触,两者在z方向变为0,如图8(c)所示。
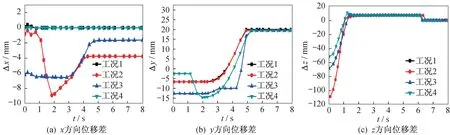
图8 抓取装置-导弹模块相对位移曲线Fig.8 Relative displacement curves of the gripping device and the missile module
在工况2中,抓取装置下放过程时先与导弹模块的左端相接触,左侧钢丝绳由拉伸转为松弛状态,而右侧钢丝绳仍处于拉伸状态,抓取装置与导弹模块之间的相对姿态差无法通过钢丝绳柔性自适应调整。此时抓取装置右端的运动轨迹是以左端接触线为转动轴,抓取装置的长度为半径的圆弧转动。左侧吊钩与吊具先接触时的碰撞弹跳和右侧绳索拉伸力作用,导致吊钩上的a1点在x方向上产生明显的滑移量位移,两点位移差最大9 mm。当抓取装置持续下放至与导弹模块完全接触时,a1点的圆弧轨迹运动停止,左、右两侧钢丝绳均处于松弛状态,抓取装置与导弹模块之间的相对姿态差和位移差能够通过钢丝绳柔性自适应调整。抓取装置与导弹模块完全接触后绳索无拉力,抓取装置倾斜导致在导弹上表面上产生向右侧的滑移,直至吊钩与吊具接触。
在工况3中,当导弹模块绕z轴旋转0.7°时,导弹模块上的吊耳与抓取装置的吊钩在y⁃z平面产生夹角。当抓取装置完全与导弹模块上平面接触时,钢丝绳完全处于松弛状态,此时抓取装置具有3 个自由度。吊钩与吊耳在2 s 开始对位,在3 s 左右由于导弹模块的位姿变化对吊钩产生了一定的阻力,迫使吊钩在x、y方向发生位置偏移,引起抓取装置产生x、y方向位移以及z方向转动。对位完成后,吊钩与吊耳在x、y方向的位移差不再变化。
在工况4中,导弹模块绕x轴倾斜2.5°时,抓取装置的运动和受力与工况2 类似。接触时的碰撞弹跳和绳索拉伸力作用,导致抓取装置吊钩上的a1点在y正方向产生明显的滑移量位移。完全接触时由于重力作用,抓取装置在y方向产生一定的滑移。
4.2.3 钢丝绳运动与作用力分析
抓取装置提升过程中钢丝绳在将导弹模块起吊拉起的一瞬间产生一定的加速度,在钢丝绳弹性和惯性力激励下,导弹模块出现了非线性振荡。在工况1 和工况4中,抓取装置吊钩高度一致,两侧钢丝绳几乎同时拉紧受力,钢丝绳拉力瞬间由0 跳变为12 000 N,如图9(b)所示。在工况2 和工况4中,两侧吊钩存在高度差,抓取装置提升过程中较低一端吊钩上的钢丝绳逐渐拉紧,先行提升,故钢丝绳拉力在约0.5 s 内逐渐增大。但在两侧钢丝绳均拉紧后,起吊加速度引起的惯性力和钢丝绳弹性导致导弹模块在起吊过程中仍会出现非线性振荡。

图9 振动曲线Fig.9 Vibration curves
5 结束语
本文采用有限段离散化方法,基于ADAMS 软件以及宏命令建立了含钢丝绳柔性环节的某导弹自动装填系统抓取装置动力学模型。仿真分析了抓取装置相对导弹模块在x、y、z方向上存在对位姿态偏差的工况下,在钢丝绳柔性和结构非线性碰撞耦合作用下,抓取装置下放-抓弹-吊弹过程的运动可行性和受力特性,验证了柔索并联式抓取装置方案具有针对对位姿态偏差的自适应调整能力,并得出以下结论:
1)采用有限段离散化方法建立钢丝绳柔性模型,可以有效模拟含钢丝绳柔性环节的某导弹自动装填系统抓取装置动力学特性;
2)抓取装置放置与导弹模块之上后,钢丝绳应处于松弛状态,以保证在抓弹过程中抓取装置能自适应与导弹模块的对位精度。
3)应减小起吊速度或控制起吊加速度,以减小快速起吊时钢丝绳弹性引起的导弹模块振荡。

