氧化锆陶瓷磨削工艺优化和粗糙度控制研究

李颂华，王科冲，孙 健，隋阳宏，韩光田，沙 勇

(1.沈阳建筑大学高档石材数控加工装备与技术国家地方联合工程实验室，沈阳 110168; 2.沈阳建筑大学机械工程学院，沈阳 110168)

0 引 言

自从《中国制造2025》纲领提出以来，工业各领域对高性能材料的需求日益增多。工程陶瓷因其具有轻质、高强度、高硬度、耐磨损、耐腐蚀、耐高温、绝缘性好、热膨胀系数小等诸多优点，已应用于制造轴承、密封环、燃气轮机燃烧器、涡轮叶片、航天器喷嘴等场合[1]。同时，由于工程陶瓷自身具有较高硬度和脆性，在加工过程中易出现裂纹、崩碎等现象，使其成为典型的难加工材料[2]。所以，探究合适的加工方法，以此来合理控制工程陶瓷表面粗糙度，对于工程陶瓷材料的运用和进一步发展具有重要的意义。

随着科技的快速发展和高新技术的需要，工程陶瓷材料日益受到广泛关注，对其加工表面质量要求也越来越高，国内外学者针对工程陶瓷磨削加工做了许多研究。Wu等[3]基于一系列SiC磨削试验，提出一种新的脆性材料表面粗糙度模型，并通过试验验证模型预测具有良好的匹配性。吴玉厚等[4]在不同冷却条件下采用金刚石砂轮磨削氧化锆工件，研究磨削参数对磨削工件表面质量的影响规律，结果表明精密磨削中氧化锆陶瓷干磨情况下表面粗糙度值小于湿磨表面粗糙度值。Sanjay[5]通过碳化硅陶瓷磨削实验研究了影响磨削表面质量的因素，并通过遗传算法对陶瓷磨削过程进行了多目标优化。李厦等[6]基于弹性变形弧长模型，运用统计学理论建立了理论切削厚度模型，推导出最大未变形切削厚度公式，并验证了公式的合理性。

迄今为止，表面粗糙度值Ra的大小仍然是用来评价磨削结果好坏的重要指标之一。在工程陶瓷精密加工方面，国内外学者也进行了大量的研究工作，但对于磨削表面粗糙度合理控制的研究较少。以某型号机床中氧化锆陶瓷零件为例，工作表面为平面，粗糙度要求Ra不超过0.25 μm。基于这一目标，本文利用正交实验相关性质，深入探究了磨削工艺参数对加工表面粗糙度的影响规律，对工程陶瓷精密磨削参数的确定、加工表面质量的合理控制具有重要的指导意义[7]。

1 实 验

1.1 原料及仪器

本次磨削实验选用ZrO2陶瓷毛坯为磨削试件，几何尺寸为20 mm×20 mm×15 mm，其主要机械性能如表1所示。实验选用树脂结合剂金刚石砂轮，性能参数如表2所示，采用水基磨削液，浓度为3.8%，流量为80 L/min。

表1 ZrO2陶瓷毛坯主要机械性能Table 1 Main mechanical properties of zirconia ceramic specimen

表2 金刚石砂轮性能指标Table 2 Performance indicators of diamond grinding wheel

1.2 磨削方法

磨削参数、磨料性能、砂轮粒度、加工方式、冷却情况等是影响磨削表面质量的主要因素[8]，合理选择加工工艺能有效提高加工效率和磨削表面质量。本文利用正交实验相关性质，选用三因素四水平L16(43)正交表进行实验，正交因素水平如表3所示。实验采用单行程切入式磨削，砂轮以顺磨的方式磨削工件表面，研究各磨削参数对ZrO2陶瓷工件表面粗糙度值Ra的影响情况。为了进一步优化氧化锆陶瓷磨削工艺参数，在正交实验结果基础上采用单因素实验法，分别研究磨削深度ap、砂轮线速度vs、工件进给速度vw对氧化锆陶瓷磨削表面粗糙度Ra的影响。

表3 正交实验因素水平表Table 3 Factors and levels of orthogonal experimental

1.3 设备及检测仪器

图1 氧化锆磨削实验图Fig.1 Experimental diagram of zirconia ceramic grinding

实验选用设备是由德国柯尔柏斯来福临公司生产的BLOHM Orbit 36 CNC精密平面成形磨床，主轴功率8.5 kW，其最小分辨率可以达到0.001 mm，最大转速为24000 r/min，最大砂轮线速度可达到70 m/s，磨削实验系统如图1所示。泰勒接触式Surtron-ic25型粗糙度仪作为测量试件表面粗糙度的仪器，测量精度可以达到0.001 μm。

在对试件表面粗糙度测量过程中，考虑到砂轮沿轴向、径向磨粒分布的均匀性、等高性差异，为了减小测量误差，选垂直工件进给方向进行测量，同时适当增大测量长度。另外，为了减小实验结果的误差，每个试件测量5组数据，5组数据中剔除最大值和最小值，实验的最终结果采用剩余3组数据的均值表示。

2 结果与讨论

2.1 正交实验结果分析

依据正交实验相关性质，对实验结果进行处理，得到表面粗糙度Ra回应表，如表4所示。根据Ra回应表，可得到正交实验结果如图2所示。

表4 Ra回应表Table 4 Response table for the surface roughness

由回应表可知，各因素对应的极差值R大小不相同，表明各因素水平大小的改变对粗糙度值Ra的影响是不一样的。极差值R越大的因素，其值的改变对粗糙度Ra影响越大。极差值R最大那一列所对应的因素，对粗糙度Ra的影响最大，在实验中需要优先考虑该因素变化对实验结果产生的影响。分析结果表明，氧化锆陶瓷磨削实验中，影响工件表面粗糙度的因素主次顺序为磨削深度>砂轮线速度>工件进给速度。

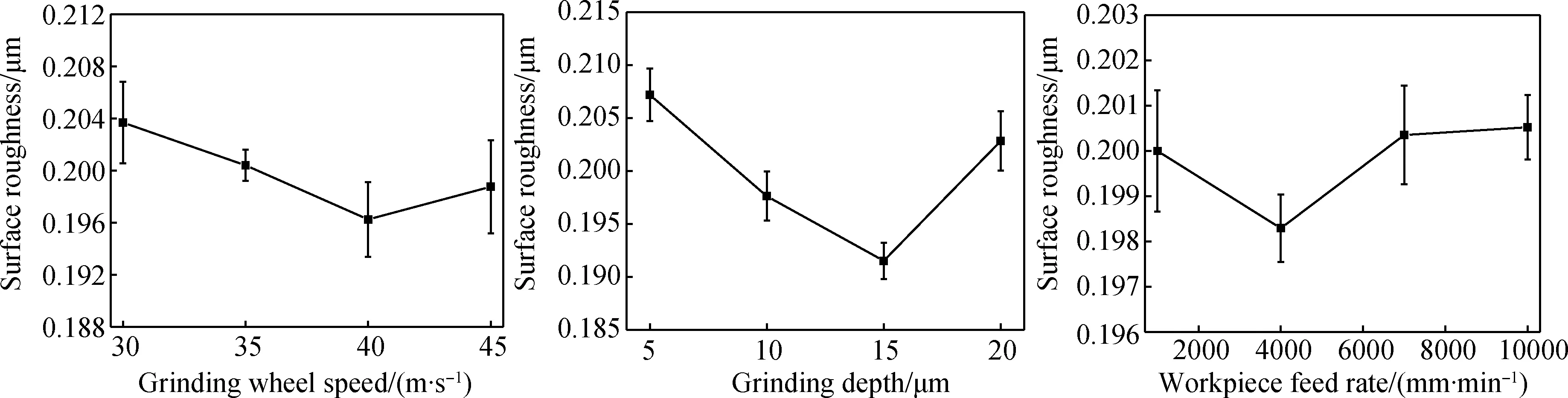
图2 磨削参数对表面粗糙度影响
Fig.2 Effect of grinding parameters on surface roughness

由趋势图可知，当砂轮对ZrO2工件表面材料进行去除时，随着金刚石砂轮线速度vs逐渐增加，ZrO2工件表面粗糙度值Ra逐渐减小；当线速度vs超过40 m/s时，工件表面粗糙度值Ra呈逐渐上升趋势；随着磨削深度ap逐渐增加，ZrO2表面粗糙度值Ra总体上呈先减小再增大的趋势，磨削深度为15 μm时粗糙度值最小；随着工件进给速度vw逐渐增加，ZrO2表面粗糙度值Ra先减小后增大，但总体变化幅度不大，变化不明显，在工件进给速度为4000 mm/min时粗糙度值Ra达到最小值。

2.2 磨削深度对表面粗糙度的影响

磨削加工实质是分布在高速旋转砂轮表面上的大量磨粒与工件表面进行微小切削作用累积的结果，砂轮与工件间的接触弧长度，是正确认识磨削加工过程的重要基本参数之一，特别是其对磨削温度、磨削表面质量等有重要影响[9]。如图3所示，工件与砂轮在这个模型中被假定为两个绝对刚体，即忽略工件或砂轮弹性变形对接触弧长的影响，然后通过几何法推导出砂轮与工件的接触弧长度表达式，即：

(1)

式中：lg为几何接触弧长度(mm)；ap为磨削深度(mm)；de为砂轮当量直径(mm)。

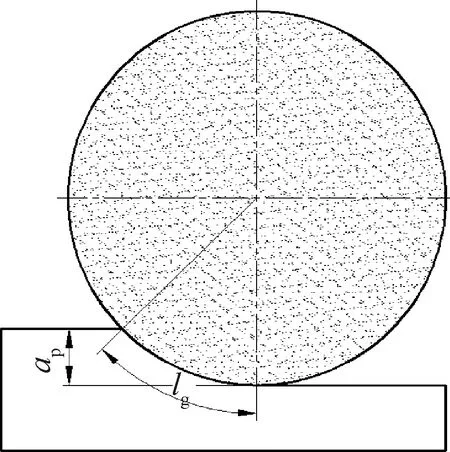
图3 几何接触弧长度模型
Fig.3 Model of geometric contact arc length

图4 磨削深度对粗糙度的影响
Fig.4 Effect of the grinding depth on surface roughness

在磨削深度单因素实验中，取砂轮线速度40 m/s，工件进给速度4000 mm/min，粗糙度Ra随磨削深度增大的变化趋势如图4所示。由图知，Ra随着磨削深度的增加而减小，当磨削深度为18 μm时，粗糙度值Ra达到最小值。随着磨削深度继续增加，粗糙度值Ra逐渐增大，并且增大趋势加快。

由式(1)可知，随着磨削深度ap增加，砂轮与工件接触弧长随之增大，磨削区接触面积增加，散热条件变差，热量积累导致磨削区温度迅速升高，工件表面材料因高温而软化，提高了氧化锆陶瓷材料的断裂韧性，增加了塑性去除所占比例，工件表面粗糙度随之减小[10]。随着磨削深度继续增加，磨粒对工件表面的划痕加深，并且磨削层厚度增加到实现材料延性和脆性去除转变的临界切深时，氧化锆陶瓷表面材料去除机理由大量的塑性去除逐步转化为以脆性去除为主，从而导致氧化锆工件表面粗糙度值升高[11]。

2.3 砂轮线速度对表面粗糙度的影响

在精密磨削加工技术中，工件表面粗糙度Ra的影响因素不计其数，磨料性能、砂轮型号、磨削参数、冷却情况、表面材料去除方式等都对工件表面粗糙Ra有一定的影响。磨削加工表面材料去除方式主要是脆性断裂还是塑性去除，由材料最大未变形切削厚度hmax与延性去除的临界切深hc二者的关系决定。研究表明，当hmaxhc时，磨削表面材料去除方式以脆性断裂去除为主。因此，在探究砂轮线速度对氧化锆陶瓷表面粗糙度的影响过程中，引入最大未变形切削厚度hmax。谢桂芝等[12]假定单个切屑截面为三角形且整个切屑不变形，hmax可表示为：

(2)

式中：C为单位面积的有效磨粒数；θ为磨粒锥顶角半角；ap为磨削深度；vs为砂轮线速度；vw为工件进给速度；ds为砂轮当量直径。

在砂轮线速度单因素实验中，取磨削深度18 μm，工件进给速度4000 mm/min，粗糙度Ra随砂轮线速度增大的变化趋势如图5所示。由图知，Ra随着砂轮线速度的增加而减小，当砂轮线速度为43 m/s时，粗糙度值Ra达到最小值。但随着砂轮线速度的持续增加，粗糙度值Ra又呈现逐渐增大的趋势，并且增大愈加明显。

由式(2)可知，随着砂轮线速度vs增大，ZrO2材料的最大未变形切削厚度hmax减小，单颗金刚石磨粒磨削力减小，比磨削能增加，氧化锆磨削时塑性去除所占比例随之增加[13]，所以氧化锆陶瓷工件表面粗糙度Ra随砂轮线速度增大而减小。当砂轮线速度增至43 m/s后，单位时间内经过工件表面的有效磨粒数增大，磨削产生的磨屑增多，附着在金刚石磨粒间的磨屑增多致使砂轮锋利程度下降，不能进行有效的正常磨削，从而降低了磨削表面质量[14]。由此可见，适当提高砂轮线速度，可以获得较好的工件表面质量。

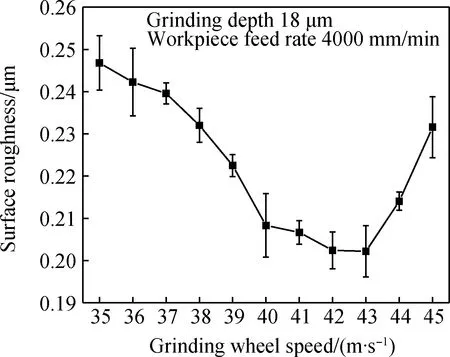
图5 砂轮线速度对粗糙度的影响
Fig.5 Effect of the grinding wheel speed on surface roughness

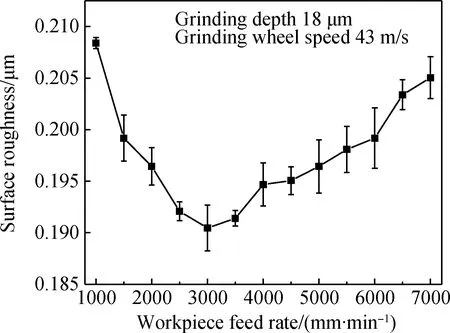
图6 工件进给速度对粗糙度的影响
Fig.6 Effect of the workpiece feed rate on surface roughness

2.4 工件进给速度对表面粗糙度的影响

在工件进给速度单因素实验中，取磨削深度18 μm，砂轮线速度43 m/s，粗糙度Ra随工件进给速度增大的变化趋势如图6所示。由图知，Ra随着工件进给速度的增加而减小，当工件进给速度为3000 mm/min时，粗糙度值Ra达到最小值。但是当工件进给速度超过3000 mm/min时，工件表面粗糙度值Ra有略微增大的趋势。

这是因为当工件进给速度vw较小时，砂轮切向磨削力较小，砂轮与工件间摩擦生热较少，磨削区温度较低。随着工件进给速度增大，切向磨削力增大使温升增大，塑性去除所占比例增多，表面粗糙度减小。当工件进给速度超过3000 mm/min时，砂轮与工件相互接触时间非常短，磨削区热量积累较少，工件温升较低，温度对工件表面材料去除方式影响较小，材料脆性去除占比增大，磨削表面质量变差，表面粗糙度值增大[15]。实践证明，适当增大工件进给速度有助于提高加工效率，并获得较好的工件表面质量。

2.5 最优磨削参数选择

在本文实验中，选择磨削表面粗糙度值Ra为实验指标，粗糙度值Ra越小越好，因此选择最优磨削参数时要尽可能选择Ra小的参数。由单因素实验可知，磨削深度为18 μm，砂轮线速度43 m/s，工件进给速度为3000 mm/min时，金刚石砂轮磨削ZrO2工件表面粗糙度Ra值最小，为0.1905 μm，检测结果如图7所示。因此，在当前实验条件下，金刚石砂轮磨削氧化锆陶瓷推荐最优磨削参数为：磨削深度为17～19 μm，砂轮线速度42～44 m/s，工件进给速度为2500～3500 mm/min，表面粗糙度Ra可以控制在0.2 μm以内。

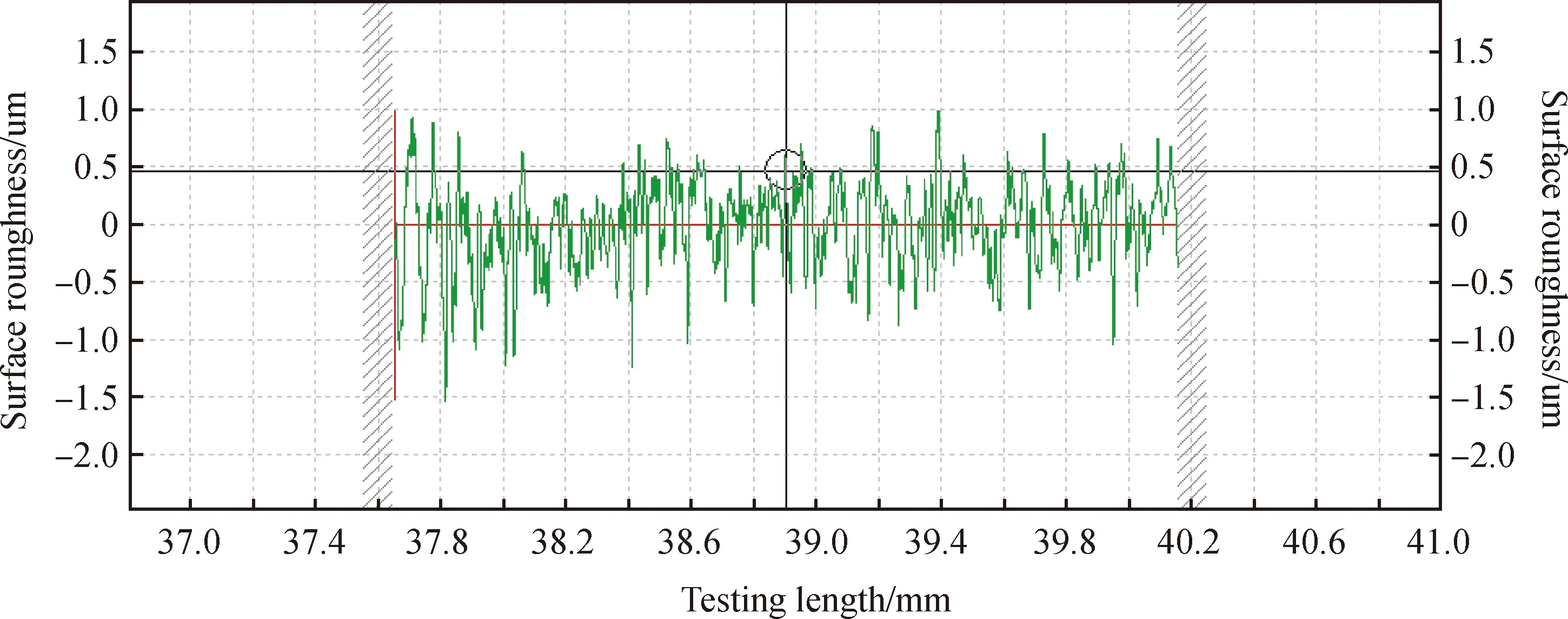
图7 表面粗糙度检测结果
Fig.7 Surface roughness test result

3 粗糙度经验公式的建立

3.1 磨削加工表面粗糙度经验公式

研究表明，影响表面粗糙的各因素与表面粗糙度间存在着复杂的指数关系，考虑到本文磨削条件后，提出简化的粗糙度表达式:

(3)

式中：C为与砂轮、磨削温度、磨削条件等因素有关的综合影响系数；k1、k2、k3分别为各磨削参数的待定指数。

由于公式(3)为非线性表达式，为了简化计算，将上述表达式两端取对数转化为线性表达式，即lnRa=lnC+k1lnvs+k2lnap+k3lnvw，记为y=k0+k1x1+k2x2+k3x3，即k0=lnC，x1=lnvs，x2=lnap，x3=lnvw。为了计算k0、k1、k2、k3，可利用正交实验中16组实验数据建立以下线性回归矩阵方程:

Y=XK+ε

(4)

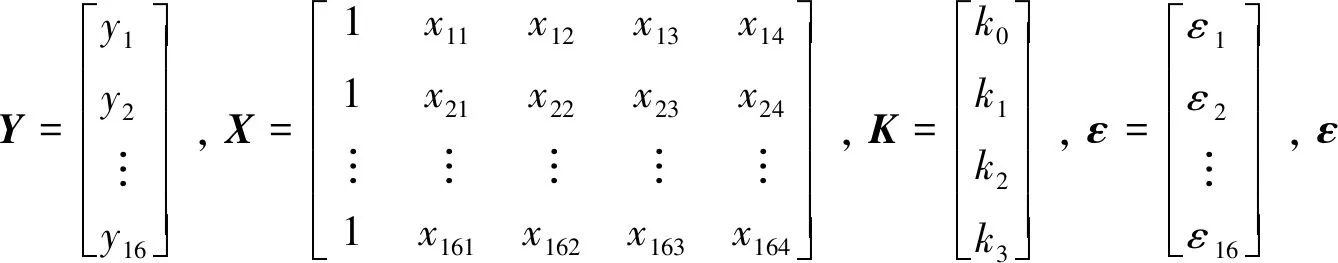
利用最小二乘法原理计算k0、k1、k2、k3，则K的最小二乘估计量为K=(XTX)-1XTY，利用Matlab中提供的regress函数进行计算[16]，可得:

K=[-1.4922 -0.0724 -0.0293 0.0013]T

(5)

经计算可得简化的粗糙度表达式为:

(6)

3.2 测量值与预测值比较

为了验证粗糙度表达式是否正确，现将各组实验的磨削参数带入式(6)中可得到相应的预测值，测量值与预测值比较如表5所示。

表5 粗糙度测量值与预测值比较Table 5 Compare roughness measurements with predicted values

经比较可知，预测值与测量值最小相对误差为0.27%，最大相对误差4.69%，所以粗糙度经验公式对于氧化锆陶瓷磨削具有较好的预测效果，达到了预测磨削表面粗糙度的目的。在实际生产加工中，只要各磨削参数取值合理，可以实现对磨削表面粗糙度在一定范围内进行控制，为实际生产加工提供一定的理论指导[17]。

4 结 论

(1)在氧化锆陶瓷磨削加工过程中，磨削深度对工件表面粗糙度影响最大，接下来是砂轮线速度，工件进给速度对粗糙度值的影响不明显。

(2)当前实验条件下，磨削氧化锆陶瓷推荐最优参数组合为：磨削深度为17～19 μm，砂轮线速度42～44 m/s，工件进给速度为2500～3500 mm/min，表面粗糙度Ra可以控制在0.2 μm以内。

(3)经验公式具有较好的预测效果，合理选择磨削参数可以对氧化锆陶瓷磨削表面粗糙度进行预测和控制，对生产加工具有重要意义。