碳化环境混凝土结构的耐久性定量分析模型
余 波,李启明,刘姝妲
(1.广西大学土木建筑工程学院,南宁 530004;2.工程防灾与结构安全教育部重点实验室,南宁 530004; 3.广西防灾减灾与工程安全重点实验室,南宁 530004)
0 引 言
混凝土碳化会引起混凝土内部的碱性降低,从而诱导混凝土中的钢筋发生锈蚀,对混凝土结构的耐久性产生不利影响。准确分析和预测混凝土碳化深度对于钢筋混凝土结构的耐久性分析、设计和评估具有重要意义。在目前的研究中,混凝土碳化分析模型主要分为经验模型和理论模型。其中,经验模型[1-3]主要基于特定的试验数据,通过拟合分析建立碳化深度与混凝土材料和环境参数之间的经验关系,具有计算简便的优点,但是无法揭示碳化机理,而且仅适用于特定的材料组分和环境条件;理论模型[4-6]考虑了混凝土碳化反应中的传输过程和化学反应过程,具有相对严密的理论推导过程,但是所涉及的物理化学参数难以准确求解,并且难以合理考虑环境条件对混凝土碳化的影响,导致适用性有限。因此,有必要研究建立一种能够综合考虑环境条件和材料因素影响的混凝土碳化分析模型。
鉴于此,本文根据水泥水化和混凝土碳化的物理化学反应过程,结合混凝土中二氧化碳、氢氧化钙和水化硅酸钙的物质的量守恒定律,综合考虑材料因素(如胶凝材料用量、水胶比、矿物掺合料等)和环境条件(如温度、相对湿度和CO2浓度)等因素的影响,研究建立了混凝土碳化多场耦合数值分析模型的控制方程及其初始条件和边界条件,并定量分析了模型参数取值对计算精度和计算效率的影响规律。
1 混凝土碳化多场耦合数值分析模型
1.1 控制方程及其边界条件和初始条件
根据水泥水化反应和混凝土碳化反应机理[7-9],考虑混凝土中气相CO2、固相和液相Ca(OH)2(简称CH)、固相和液相3CaO·2SiO2·3H2O(简称CSH)的物质的量守恒,可以建立混凝土碳化多场耦合数值分析模型的控制方程[10]:
(1)
(2)
(3)
式中,t为碳化时间(s);x为混凝土内某点到混凝土外表面的距离(m);DCO2(x,t)为CO2在混凝土中的扩散系数(m2/s);CCO2(x,t)、CCH(x,t)和CCSH(x,t)分别为CO2、Ca(OH)2和3CaO·2SiO2·3H2O的摩尔浓度(mol/m3);kCH与kCSH分别为CH和CSH参与碳化反应的速率系数(m3/(mol·s))。
此外,混凝土碳化多场耦合数值分析模型的初始条件和边界条件分别为:
初始条件:
(4)
(5)
(6)
边界条件:
(7)
(8)
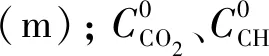
1.2 混凝土碳化分析的模型参数
对于比较常用的复掺矿物掺合料混凝土,碳化分析涉及以下模型参数:水泥中CH和CSH的初始摩尔浓度、矿物掺合料中CH和CSH的初始摩尔浓度、CH和CSH反应速率系、CO2气体扩散系数。下面从化学物质平衡的角度,建立各物质的摩尔浓度关系式,进而确定上述模型参数。
由水泥水化反应和碳化反应机理可知,当水泥完全水化时,3CaO·SiO2(简称C3S)和2CaO·SiO2(简称C2S)全部被消耗,可碳化物质主要是CH和CSH。完全水化后,单位体积混凝土中CH和CSH物质的量分别为[11]:
(9)
(10)
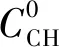
1.2.1 水泥中CH和CSH的初始浓度
根据水泥水化的化学方程式可知,C3S和C2S发生水化反应生成CH,又由于碳化反应4CaO·Al2O3·Fe2O3(简称C4AF)和3CaO·Al2O3(简称C3A)消耗CH。根据混凝土溶液中CH和CSH的物质浓度平衡关系可知,水泥完全水化生成各可碳化物质的摩尔浓度为[11]:
(11)
(12)
式中,βf、βbs和βs别为粉煤灰掺量、矿粉掺量、硅粉掺量;B为单位体积胶凝材料用量(kg/m3)。
对于普通硅酸盐水泥,可以将混合材料掺量近似取为α′=15%[12],则普通硅酸盐水泥水化反应生成的CH和CSH摩尔浓度分别为:
(13)
(14)
1.2.2 矿物掺合料中CH和CSH的初始浓度
根据粉煤灰中各氧化物与CH发生水化反应的物质平衡关系,结合粉煤灰主要化学成分[13],可以确定粉煤灰发生二次水化反应时CH和CSH的摩尔浓度改变量分别为:
(15)
(16)
式中,[CaO]、[SiO2]和[Al2O3]分别为CaO、SiO2和Al2O3的摩尔浓度;γ为粉煤灰二次水化反应程度系数。
根据矿粉中各氧化物与CH发生水化反应的物质平衡关系,将矿粉中CaO、SiO2和Al2O3的质量分数近似取为40%、33%和12%[4],可以得到矿粉发生二次水化时CH和CSH的摩尔浓度改变量分别为:
(17)
(18)
式中,η为矿粉二次水化反应程度系数。
硅灰的主要成分为SiO2,在水化过程中消耗CH生成了CSH,根据SiO2与CH发生水化反应的物质平衡关系,可以确定硅灰中CH和CSH的摩尔浓度改变量分别为:
(19)
(20)
式中,λ为硅灰的二次水化反应程度系数。
1.2.3 CO2扩散系数及CH和CSH反应速率系数
由于碳化反应生成的碳酸钙沉淀物堆积在混凝土孔隙中,使得CO2在混凝土孔隙中的扩散速率减慢,所以混凝土中CO2扩散系数为[11]:
(21)
式中,De为准环境下混凝土中CO2扩散系数(m2/s);εp为混凝土孔隙率,其计算公式为[12]:
(22)
式中,RW/B为水胶比;B为胶凝材料用量(kg/m3)。
CH的反应速率即为CO2与CH反应生成CaCO3的速率,考虑温度变化对碳化反应速率的影响规律,文献[14]提出CH的反应速率系数为:
(23)
式中,kCH为CH碳化的反应速率系数,单位为m3/(mol·s);β为修正系数,取1390 m3/(mol·s);U为扩散反应能量,混凝土中CO2的扩散反应能量通过试验确定约为40000 J/(mol·K);R为气体摩尔常量,取8.314 J/(mol·K);T为实际环境温度,单位为K;Rr为相对湿度RRH对于碳化反应速率kCH的理论修正函数[15]。
根据文献[16]的研究成果,CH和CSH的反应速率系数之间的比值近似为7.8×10-3,因此CSH的反应速率系数可以近似为:
(24)
1.3 多场耦合数值分析模型的求解
混凝土碳化分析的多场耦合数值模型的计算步骤如下:
(1)输入基本参数
输入CO2初始体积分数C0、温度T、相对湿度RRH、胶凝材料用量B、水胶比RW/B、粉煤灰掺量βf、矿渣掺量βbs、硅灰掺量βs、碳化时间t、计算深度h、时间步长Δt、空间步长Δx。
(2)计算模型参数初始值
CCO2=41.57×C0
(25)
(3)对空间网格开展循环计算
当时刻i=1时,令i-1时刻CO2浓度值CO2(i-1,j)等于i时刻CO2浓度值CO2(i,j),通过式(2)~(3)计算i时刻各位置的CH浓度CCH(i,j)、CSH浓度CCSH(i,j),进而计算CO2扩散系数De(i,j)、孔隙率εp(i,j)和pH值pH(i,j)。利用有限差分法,通过引入参数α、β求得i时刻不同位置CO2浓度CO2(i,j):
CO2(i,j)=βj-1CO2(i,j-1)(j=N-1,…,3,2,1)
(26)

(4)判断CO2(i,j)是否收敛
若该值收敛,则可求解对应的碳化深度,进入下一步计算;若不收敛,则利用计算出的CO2(i,j)返回第(3)步再次迭代。
(5)跳出空间网格迭代后,进入时间网格循环计算

2 碳化分析模型的参数敏感性分析
2.1 时间步长和空间步长的影响
本文利用有限差分法求解混凝土碳化多场耦合数值分析模型,模型参数中的时间步长Δt和空间步长Δx的选取,对于模型求解的计算精度和效率有重要影响。为了定量分析Δt和Δx对模型计算精度的影响规律,选取了文献[18-27]中的64组室内标准碳化环境下的混凝土碳化深度试验数据,结合时间步长Δt和空间步长Δx的不同取值组合,通过模型计算值与试验测试值的对比,分析时间步长Δt和空间步长Δx对模型计算精度的影响。不失一般性地从64组试验数据中任意选取一组试验数据来进行对比分析,已知该组试验数据为普通硅酸盐混凝土,水泥用量为420 kg/m3,水灰比为0.6,温度为20 ℃,相对湿度为70%,CO2浓度为20%,碳化时间为28 d,碳化深度为7.7 mm,取不同时间步长和空间步长时由数值模型所计算的碳化深度见表1,数值模型的计算值与试验值之间的相对误差见表2。表中,Nt为碳化时间28 d的等分份数。
结合表1和表2可知,在时间步长保持不变的情况下(即Nt为定值),空间步长Δx的取值越小,空间网格划分越细密,模型计算值越趋接近于试验值;在空间步长Δx保持不变的情况下,时间网格划分越细(即Nt越大时),模型计算值越趋接近于试验值,此处Nt最大值所对应的时间步长Δt=3.36 h;当Nt的取值保持不变,Δx分别取0.05 mm、0.1 mm和0.2 mm时,碳化深度的计算精度已达到小数点后两位,可以认为Δx取0.05 mm、0.1 mm和0.2 mm时已经能够保证足够的计算精度。因此,综合考虑混凝土碳化分析多场耦合数值模型的计算精度和计算效率,推荐时间步长取Δt=3.36 h和空间步长取Δx=0.2 mm。

表1 取不同时间步长和空间步长时碳化深度计算值Table 1 Calculated values of carbonation depth for different time and space steps /mm

表2 取不同时间步长和空间步长时碳化深度计算值与试验值之间的相对误差Table 2 Relative error between calculated and tested carbonation depth for different time and space steps /%
2.2 矿物掺合料二次水化程度系数的影响

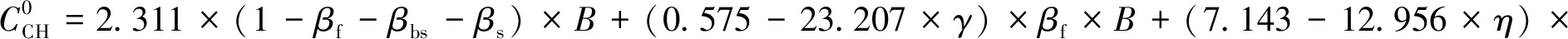
(27)
(28)
式中,γ、η和λ分别为粉煤灰、矿粉和硅灰的二次水化反应程度系数。
为了对矿物掺合料二次水化反应程度系数开展灵敏度分析,参考文献[28-31]的研究结果,结合模型的适用范围,将粉煤灰的二次水化反应程度系数γ分别取值为0.06、0.08和0.1,矿粉的二次水化反应程度系数η分别取值为0.2、0.3和0.4,硅灰的二次水化反应程度系数λ分别取值为0.3、0.4和0.5。选取文献[12,18-27]中的63组数据,将上述矿物掺合料二次水化反应程度系数的不同组合值代入混凝土碳化多场耦合数值分析模型,可以确定模型计算值与试验测试值的散点分布。限于篇幅,以γ分别取0.06、0.08和 0.1,η分别取0.2和0.3,λ分别取0.3和0.4这12种情况为例,散点分布如图1所示。由图1可以看出,当选取不同的粉煤灰、矿粉和硅灰的二次水化反应程度系数组合,对混凝土碳化分析多场耦合数值模型的计算精度有着重要影响。总体来看,当η和λ保持不变时,随着γ的增大,模型计算值与实测值越接近,并且当γ=1时,模型预测值大部分分布在等值线附近,说明此时计算精度较高。

图1 取不同矿物掺合料水化程度系数时碳化深度的计算值与试验值对比
Fig.1 Comparison between calculated and tested carbonation depth for different coefficients of the degree of hydration of mineral admixtures
为了进一步对比分析不同的矿物掺合料二次水化反应程度系数对混凝土碳化分析多场耦合数值模型计算精度的影响,计算了27组不同的矿物掺合料二次水化反应程度系数组合下模型预测值和试验值比值的均值和标准差,计算结果见表3。由表3可知,随着粉煤灰的二次水化反应程度系数γ的增大,模型预测值和试验值比值的均值增大趋势最为明显,说明粉煤灰的二次反应水化程度系数γ对碳化深度的计算值影响最大。相比而言,硅灰和矿粉对碳化的二次水化反应程度系数对模型计算精度的影响不大。总体而言,当矿物掺合料水化反应程度系数组合为γ=0.06、η=0.3和λ=0.5模型预测值与试验值的计算结果较为接近,且二者的比值的标准差较小(标准差为0.3022),说明模型的计算精度较好。因此,为了保证混凝土碳化多场耦合数值分析模型的计算精度,可以将矿物掺合料水化反应程度系数分别取γ=0.06、η=0.3和λ=0.5。

表3 模型预测值和试验值比值的均值和标准差Table 3 Mean and standard deviation of the ratio of predicted and experimental values
3 对比分析与验证
为了确定本文混凝土碳化多场耦合数值分析模型的计算精度,选取文献[12,18-27,31]中101组标准碳化环境(温度为(20±5) ℃,相对湿度为(70±5) ℃,CO2浓度为(20±3) ℃,碳化时间为28 d)下混凝土碳化数据试验值,并与文献[4,6,32-34]中的5种混凝土碳化分析模型进行对比分析。不同碳化分析模型的计算值与试验测试值的计算结果对比分析如图2所示。由图2可知,文献[4]模型和文献[34]模型的计算值与试验值相比偏大且较为离散,往往会高估混凝土的碳化深度;文献[6]模型的计算值总体效果较好,但是部分计算值偏大,所预测的混凝土碳化深度也存在部分高估的情况;文献[32]模型和文献[33]的计算值均低估了混凝土的碳化深度,预测结果偏于危险。另外,文献[4]、[6]模型属于理论模型,其中部分模型参数难以测得,不便于实际工程应用;文献[32]模型、文献[33]模型、文献[34]模型均属于经验模型,是通过有限的试验数据拟合得到的,其模型适用性有限。综合看来,本文碳化分析模型具有相对严密的理论基础,且综合
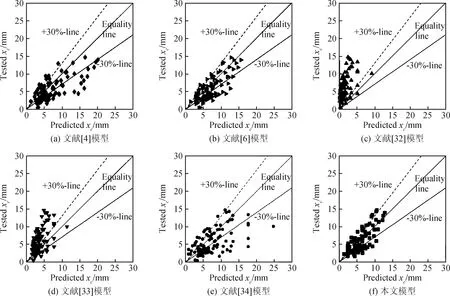
图2 标准环境下本文模型与其它模型的对比
Fig.2 Comparison between proposed and other models under standard environment
考虑了材料因素(如胶凝材料用量、水胶比、矿物掺合料等)和环境条件(如温度、相对湿度和CO2浓度)等因素的影响,模型参数取值方便,且其计算值与试验值吻合良好,具有较高的计算精度和适用性。
4 结 论
根据水泥水化和混凝土碳化的物理化学反应过程,综合考虑材料因素和环境条件的影响,研究建立了混凝土碳化多场耦合数值分析模型及其初始条件和边界条件,定量分析了时间步长、空间步长、矿物掺合料二次水化反应程度系数对碳化分析模型的计算精度和计算效率的影响规律。分析结果表明:
(1)时间步长和空间步长的取值对混凝土碳化多场耦合数值分析模型的计算精度和计算效率密切相关。随着时间步长和空间步长的减小,多场耦合数值分析模型的计算精度逐渐提高,但是计算量也随之增大;为了兼顾计算精度和计算效率,建议将时间步长和空间步长分别选取为Δt=3.36 h和Δx=0.2 mm。
(2)对于粉煤灰、矿粉和硅灰三种矿物掺合料,粉煤灰的二次水化反应程度系数对混凝土碳化深度的影响相对较大,而矿粉和硅灰的二次水化反应程度系数对混凝土碳化深度的影响相对较小;当粉煤灰、矿粉和硅灰二次水化程度系数组合为γ=0.06、η=0.3和λ=0.5时,混凝土碳化分析多场耦合数值模型的计算值与试验测试值比值的均值和标准差分别为1.0547和0.3022,说明此时模型计算精度较好。
(3)通过与101组标准碳化环境下试验数据和5种混凝土碳化分析模型进行对比分析,发现本文模型具有相对严密的理论基础,能够综合考虑材料因素(如胶凝材料用量、水胶比、矿物掺合料等)和环境条件(如温度、相对湿度和CO2浓度)的影响,具有较高的计算精度和适用性。

