SVM和BP检测滨海湿地土壤有机质

张 森, 卢 霞*, 聂格格, 李昱蓉, 邵亚婷, 田燕芹, 范礼强, 张钰娟

1. 江苏海洋大学测绘与海洋信息学院， 江苏 连云港 222005 2. 河南财经政法大学资源与环境学院， 河南 郑州 450046

引 言

土壤中的有机质是湿地土壤成分中的重要组成部分， 是判别湿地中土壤肥力大小的重要指标[1]。 因此快速测定湿地土壤中有机质的含量， 对于维护湿地生态平衡， 可持续发展具有重要的意义。 传统检验土壤中养分含量的方法主要是基于化学分析， 费时耗力， 不能满足快速、 低成本的现实需求， 而光谱分析正好弥补了传统式化学分析方法的不足， 为估算土壤中的各种养分含量提供了有力的技术支持。

目前利用光谱分析来估算土壤中养分含量的研究主要分为三个步骤： (1) 将测得的原始光谱数据进行光谱预处理， 以消除或减弱原有光谱信息中的噪声， 放大有用信息， 比较常见的光谱预处理方法有连续投影法(SPA)[2-3]、 Savitzky-Golay卷积平滑算法[4]、 微分算法[5]、 指数变换[6]等； (2) 将预处理后的光谱提取特征波段， 常用的提取方法主要有相关系数法[7]、 逐步回归法、 遗传算法[8]等； (3) 将特征波段的光谱数据和对应的土壤理化数据进行建模， 常用的建模方法主要分为线性与非线性建模， 线性建模主要有线性回归[9]、 偏最小二乘法回归[10]等； 非线性建模主要有BP神经网络[11]、 最小二乘支持向量机(LS-SVM)[12]等。 已有部分研究发现利用非线性模型来估算土壤养分含量的精度要高于线性模型， 如Bao等[13]在综合分析了不同地貌土壤有机质含量与相应光谱反射率之间的关系的基础上， 对PLS与PLS-SVM两种建模方法预测矿区土壤有机质含量的准确度做了比较， 结果表明PLS-SVM比PLS更能准确的预测。 章海亮等将光谱进行平滑、 标准归一化、 多元散射校正和一阶导数处理后， 用偏最小二乘和最小二乘支持向量机建立校正模型， 最后比较得出连续投影可见/短波近红外光谱利用最小二乘支持向量机建模是一种精确的土壤有机质和速效钾的测定方法。 然而针对滨海湿地土壤类型的非线性高光谱估算研究相对较少[14]。 滨海湿地作为一种陆地与水域之间的生态系统， 受海洋环境的影响较大， 表现出独特的土壤特性。 因此本文以江苏省大丰麋鹿野牧区滨海湿地土壤为研究对象， 利用非线性模型SVM支持向量机的建模方法并对比BP神经网络算法来估算滨海湿地土壤有机质的含量， 以此来验证滨海湿地土壤有机质含量的非线性高光谱估算模型的可行性。

1 实验部分

1.1 研究区概况

江苏省大丰麋鹿国家级自然保护区坐落于中国四大湿地(南黄海湿地、 青藏高原湿地、 东北三江平原湿地、 鄱阳湖湿地)之一的南黄海湿地上， 核心区面积4万亩， 是世界上最大的麋鹿自然保护区(32°59′—33°03′N， 120°47′—120°53′E)， 该区域主要为暖温带大陆季风性气候， 海洋性和季风性特征显著[15]； 地势平坦， 为平原盐渍沼泽， 黄河口沉积物成土母质； 第三核心区植被茂密， 分布着互花米草、 碱蓬、 芦苇等植被群落， 土壤类型主要为潮盐土与草甸滨海盐土亚类， 表层土壤含盐量在0.04%～1.13%之间[16]。

1.2 样本采集

依据研究区土壤类型和植被群落分布特征， 采用规则网格法(1 000 m×1 000 m)划分研究区， 采样方案如图1所示。 每个网格采用对角线采样法采集0～20 cm的表层土壤， 之后均匀混合， 作为该网格的土壤样本， 共采集34个土壤样本。

图1 研究区土壤采样点空间分布

将所采集的土壤样品在室温条件下自然风干， 去除石块、 残根等杂物后研磨、 过80目筛子， 保存， 用于待测土壤SOM和室内反射光谱。 土壤SOM含量测定是用水合热重铬酸钾氧化-比色法； 土壤pH范围为8.02～8.94之间， 平均值在8.4， 属于碱性土壤， 表1为34个采样点获得的土壤样品SOM的统计结果。

表1 研究区土壤样本SOM含量统计

1.3 土壤反射光谱测定

土壤反射光谱利用美国Spectra Vista 公司生产的SVC HR-1024I光谱仪进行测定。 波段范围为350～2 500 nm， 其中在350～1 000 nm光谱分辨率≤3.0 nm， 光谱间隔≤1.5 nm； 1 000～1 900 nm光谱分辨率≤9.5 nm， 光谱间隔≤3.6 nm； 1 900～2 500 nm光谱分辨率≤9.5 nm， 光谱间隔≤2.5 nm。 利用BRDF系统建立土壤测试环境： 探头垂直向下， 视场角4°， 距离土壤样品(样品盒的直径为9 cm， 高度为2 cm的圆形玻璃器皿)表面约为1 m， 室内照明光源， 为50 W的卤素灯， 天顶角45°。 测定时， 将装有土壤样品的玻璃皿放在黑色阻尼布上， 保持土壤表面平整， 每个土壤样本测量5次， 取平均值作为土壤样本反射光谱； 测量期间， 每隔15 min测定白板反射光谱以便校正。

1.4 分析方法

光谱预处理主要采用Savitzky-Golay(S-G)卷积平滑滤波与微分算法。 S-G卷积平滑滤波原理主要是采用最小二乘拟合系数来建立滤波函数， 然后对每一个窗口范围内的波长数据进行多项式最小二乘拟合， 其拟合的表达式可表示为

(1)

R′(λi)=[R(λi+1)-R(λi-1)]/2Δλ

(2)

(1/R)′(λi)=[(1/R)(λi+1)-(1/R)(λi-1)]/(2Δλ)

(3)

(4)

[lg(R)]′(λi)={[lg(R)](λi+1)-[lg(R)](λi-1)}/2Δλ

(5)

式中λi为各波段的波长， Δλ表示波长λi+1到λi的间隔[17]。 特征波段的选取是利用皮尔逊相关系数法以及相关系数的显著性检验。 为研究不同的非线性建模方法在利用高光谱反射率预测滨海湿地土壤养分含量上的精度差异， 选取支持向量机(support vector machine， SVM)与BP神经网络两种非线性模型作对比分析。

SVM建模采用台湾大学林智仁教授开发的LIBSVM工具包， BP神经网络利用MATLAB2018b软件中自带的工具包通过编程实现。 模型验证主要使用决定系数R2与均方根误差RMSE， 其中决定系数是相关系数的平方， 是一个能够直观判断拟合优势的指标， 决定系数越接近于1， 说明实测值与预测值的拟合程度越高， 模型的精度也就越佳； 均方根误差是观测值与真值偏差的平方和观测次数比值的平方根， 它对模型的建模能力和预测能力都能做出非常有效的评价， RMSE的值越小， 模型的反演能力越强。

2 结果与讨论

2.1 滨海湿地土壤光谱特性

由于原始光谱在350～400之间存在很多噪声， 因此选取400～2 400 nm波段做分析。 在MATLAB 2014b软件中利用Savitzky-Golay(S-G)滤波器将滨海湿地土壤的原始光谱进行5点平滑滤波处理， 处理后的光谱反射率曲线如图2所示， 可以看出经过自然风干的34个土壤样本测得的光谱曲线走势具有很大的相似性， 但是由于每个土壤样本中的有机质含量等土壤理化性质的不同， 所测得的土壤样本光谱反射率在波峰、 波谷、 反射率强弱上还是有所不同， 这与章海亮等的研究结果相同。 总体波段范围内的反射率介于0.1～0.7之间； 同时可以清楚的发现在1 400和1 900 nm两个波段附近有两个明显的吸收谷， 在700和1 000 nm两个波段附近有两个比较弱的吸收谷， 这主要是由土壤中的水分子振动的倍频与合频所产生的； 在1 950～2 400 nm波段内光谱曲线呈现波浪式状态， 主要是由于土壤样本中的少量水分与空气中的水分吸收产生的， 这与研究土壤光谱反射率特征的相关报道一致[2-3]。 总体上看土壤反射率随着波长的增加而不断增大， 其中在400～600 nm波段范围上升速度比较明显， 600～800 nm波段之间呈现中等缓慢上升， 800 nm以后波谱反射率上升比较平缓。

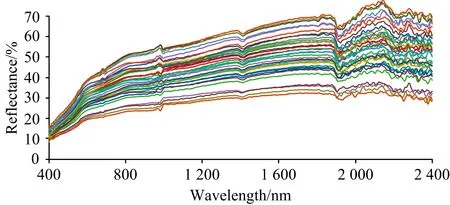
图2 S-G滤波后土壤样本反射率曲线

2.2 土壤SOM含量的特征波段提取

将S-G滤波后的光谱反射率进行四种微分变换， 并与土壤实测的34个土壤样本组的SOM含量做相关性与显著性分析， 如图3所示， 其中(a)图为一阶微分变换后的相关系数， (b)图为倒数的一阶微分后的相关系数， (c)图为倒数的二阶微分后的相关系数， (d)图为对数的一阶微分后的相关系数。 从图3可以发现四种光谱变换形式不同程度上改变了原始光谱与土壤有机质含量的相关系数， 并且将有关土壤有机质的敏感波段处的反射率进一步放大， 同时可以发现在700， 1 000， 1 400和1 900 nm几处光谱吸收谷附近的相关性都比较低， 这说明土壤受水分影响会降低光谱反射率与土壤有机质含量的相关系数。

图3 变换后的光谱与SOM含量的相关性

挑选出置信水平p<0.01的波长作为特征波段， 筛选结果如表2所示。 由表2可知： 每一种微分变换后所提取出的特征波段的数量不同， 并且每一种微分变换后与对应的土壤SOM养分含量相关性也不同。 相关性最高的是(1/R)′光谱变换形式， 所提取到的特征波段数有13个， 分别为498～501， 1 180～1 182， 1 946， 1 947和2 323～2 326 nm， 其中在2 324 nm波段附近呈现正相关性， 在500 nm波段附近主要呈现负相关性。

但是提取到的敏感波段与章海亮等利用连续投影法所提取的水稻土、 砖红土和黄土有机质敏感波段362， 392， 422， 437， 537， 652， 702和1 062 nm有所不同。 差异的原因可能是由于研究区土壤类型的不同， 前人研究结果发现大丰麋鹿国家级自然保护区第三核心区的土壤类型主要为潮滩盐土和草甸海滨盐土， 这两种土壤类型通常含盐量在0.8%～2.0%之间， 最高甚至可达4%的含盐量[18]， 而土壤盐分含量会影响土壤的反射率， 也会影响到土壤中有机质的光谱信息[6]。

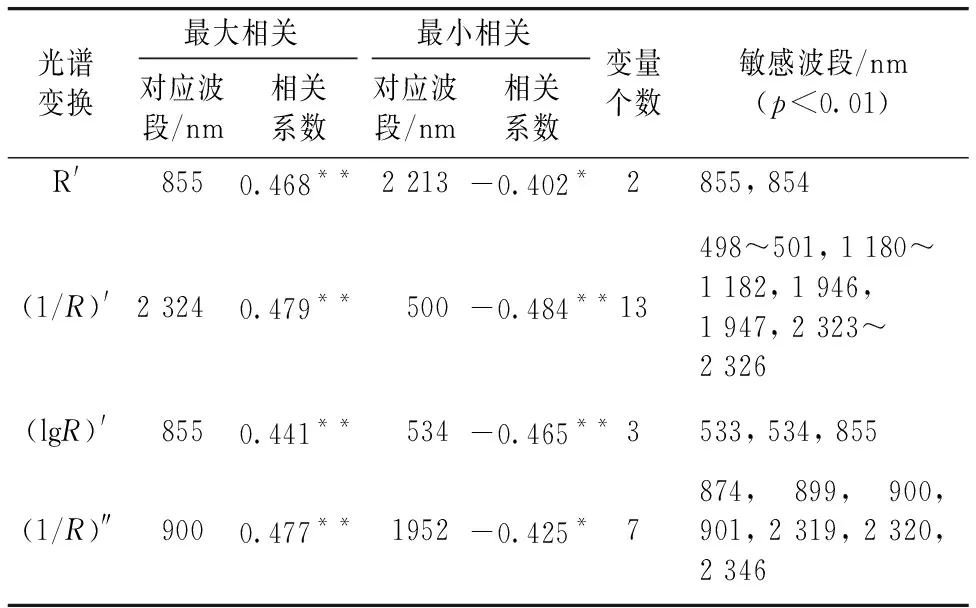
表2 土壤SOM含量的特征波段筛选

Note： *p<0.05， **p<0.01

2.3 模型的构建与精度验证

2.3.1 基于SVM支持向量机的土壤有机质含量高光谱估算模型

训练集与测试集的设置是随机选取34个土壤样本中24个光谱变换后筛选出来的特征波段数据和对应的土壤SOM含量值作为训练集的输入与输出， 剩下的10个样本作为测试集的输入与输出。 并利用MATLAB中的mapminmax函数将训练集与测试集的数据进行归一化处理， 使其映射到[0, 1]区间内。 在SVM的创建与训练中， “-t”核函数类型选择为RBF核函数， 利用网格搜索交叉验证的方法遍历c与g的值来获取最佳c与g参数， “-s”即SVM类型选择为e-SVR类型， “-p”设置e-SVR类型中损失函数p的值为0.01。 最后利用svmpredict函数和已经训练好的模型预测出剩余10个样本的有效值， 并将预测值进行反归一化处理以便更好的还原真实值。 最后构建的模型验证精度如表3所示。 由表3可知： 土壤样本反射率(1/R)′变换形式估算土壤有机质含量的精度最高， 预测决定系数R2为0.93， 预测均方根误差为0.23。

表3 SVM建模方法得到的土壤SOM含量精度

Note： *p<0.05， **p<0.01

2.3.2 基于BP神经网络的土壤有机质含量高光谱估算模型

BP神经网络的建模形式与SVM类似， 都需要设置训练集与测试集， 为方便观察对比两种建模精度， 选取与SVM建模一样的测试集与训练集； 同时与SVM建模相同， 将训练集与测试集都进行归一化处理将其映射到[0.1]区间内； 在创建神经网络时， 训练方式选择梯度下降方法， 迭代次数设置为1 000次， 训练目标设置为le-30即训练的均方根误差小于le-30， 神经元设置为10个， 学习率设置为0.01； 之后的仿真测试与反归一化和SVM建模相同。 最后构建的模型精度如表4所示。 由表4可知： 土壤样本反射率(1/R)′形式估算土壤有机质含量的精度较高， 其中预测决定系数R2为0.87， 预测均方根误差为0.33。

表4 用BP神经网络建模方法得到的土壤SOM含量精度

Note： *p<0.05， **p<0.01

2.3.3 SVM和BP检测土壤有机质含量的精度对比

图4为SVM与BP神经网络两种非线性建模方法在估算滨海湿地土壤有机质含量的精度对比， 横坐标代表四种不同的光谱变换形式， 纵坐标左侧代表决定系数R2的值， 纵坐标右侧代表RMSE的值。

图4 土壤SOM含量的建模精度对比

由图4可知： 基于决定系数R2和均方根误差RMSE评价指标， SVM支持向量机估算滨海湿地土壤有机质含量精度明显优于BP神经网络。 为了更加直观的看出SVM模型的预测效果， 用光谱变换(1/R)′构建SVM模型所预测的滨海湿地土壤有机质含量与实测的含量进行对比， 如图5所示， 横坐标为实测值， 纵坐标为预测值。 由图5可以看出SVM预测土壤有机质含量精度较好， 均匀分布于y=x直线附近。

由以上分析结果表明： 通过SVM支持向量机检测土壤有机质的精度要优于BP神经网络， 这与蒋璐璐等[19]通过最小二乘支持向量机与BP神经网络构建的浙江省衢州红壤和海宁青紫泥中氮磷钾含量的估算模型结果一致。 通过光谱的(1/R)′变换形式构建的SVM估算模型在预测滨海湿地土壤有机质的精度最高， 其中预测决定系数R2为0.93， 均方根误差RMSE为0.23， 这比刘雪梅[20]通过一阶微分结合最小二乘回归方法构建的江西省遂川县枚江乡土壤有机质含量的预测精度(R2为0.825 5)要高。 这说明基于高光谱反射率的微分变换形式所构建的SVM模型在预测滨海湿地中土壤有机质含量具有一定的可行性， 但该模型是否可以预测其他地区的滨海湿地土壤中有机质的含量还需进一步的验证。

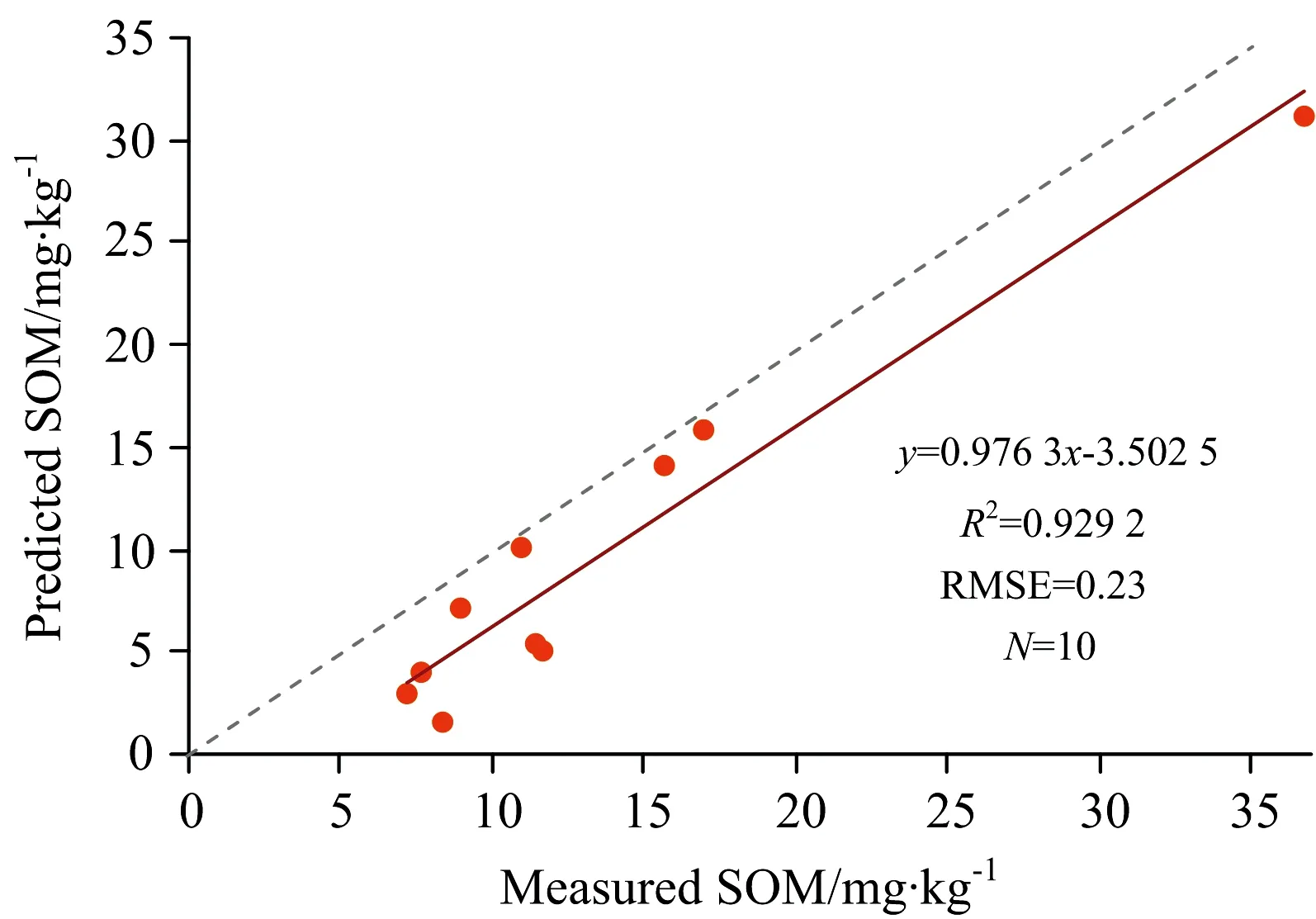
图5 土壤SOM含量预测

4 结 论

滨海湿地采集的34个土壤样本在室内测得的原始光谱进行S-G滤波处理与R′， (1/R)′， (1/R)″， (lgR)′四种微分变换， 利用相关系数法提取土壤SOM含量在高光谱遥感中的特征波段， 并通过SVM支持向量机和BP神经网络估算滨海湿地土壤中SOM含量。 得出以下结论：

(1)SVM支持向量机检测滨海湿地土壤有机质含量的精度明显优于BP神经网络模型， 利用可见-近红外高光谱构建的SVM非线性模型来快速估算滨海湿地土壤中的养分含量具有一定的可行性。

(2)土壤有机质与光谱反射率倒数的一阶微分存在较高的相关性， 显著相关(p<0.01)的波段数为13个， 敏感波段为498～501， 1 180～1 182， 1 946， 1 947和2 323～2 326 nm。

(3)基于SVM构建土壤有机质的估算模型精度最高， 预测决定系数R2为0.93， 均方根误差RMSE为0.23。

(4)光谱数据的预处理与变换形式以及模型的构建方式和样本的数量都是影响最终预测精度的重要因子， 本实验由于样本数量有限并不能很好的展示样本大小对模型估算精度的影响程度， 因此未来应深入探讨土壤样本数量对估算模型的精度和均方根误差的影响程度。