基于MPD-4电子学插件的液体闪烁体中子光响应特性实验研究

任 杰，阮锡超，黄翰雄，聂阳波，鲍 杰，李 霞

(中国原子能科学研究院 核数据重点实验室，北京 102413)

在中子物理实验和中子核技术应用中，中子能谱测量非常重要。目前常用的中子能谱探测器有中子飞行时间谱仪、3He/6Li夹心谱仪、反冲质子探测器、阈探测器、Bonner球等[1]。其中，中子飞行时间法是精度最高的中子能谱测量方法，但依赖脉冲中子源；3He/6Li夹心谱仪的探测效率太低，对2.5 MeV中子的探测效率仅为3×10-6；阈探测器需较多的活化片才能满足测量精度；Bonner球需仔细优化慢化体厚度和材料，且十分依赖解谱算法。相比之下，反冲质子探测器具有系统简单、中子探测效率高、粒子甄别能力强等优点，且n-p散射截面是标准截面，通过优化数据处理方法可得到较高的精度。液体闪烁体探测器是目前使用最广泛的反冲质子探测器之一，常用于中子能谱测量。中子光响应是液体闪烁体探测器的重要参数，表征一定能量的反冲质子在闪烁体中产生的光强度。一般将中子能量En与产生相同光强度的电子能量Eee的对应关系作为中子光响应函数。一般认为，同一种探测器的光响应函数是不变的，可在不同实验中使用相同的光响应函数。

近年来，一种专门用于液体闪烁体中子探测器的高集成度新型电子学插件(Mesytec公司的MPD-4)被广泛应用于中子探测系统中[2]，该电子学插件集成了脉冲高度(PH)和脉冲形状甄别(PSD)测量功能，且1个NIM插件即可实现4路探测器的同时测量，得到了广泛的应用，尤其是在一些中子探测器个数较多的中子探测器阵列中，该电子学系统被广泛使用。但多次实验发现，使用该电子学系统与传统电子学相比，光响应函数及探测效率存在明显差异，因此需针对此电子学系统重新测量光响应函数，并对比不同类型的电子学对液体闪烁体光响应函数的影响。

1 实验布局

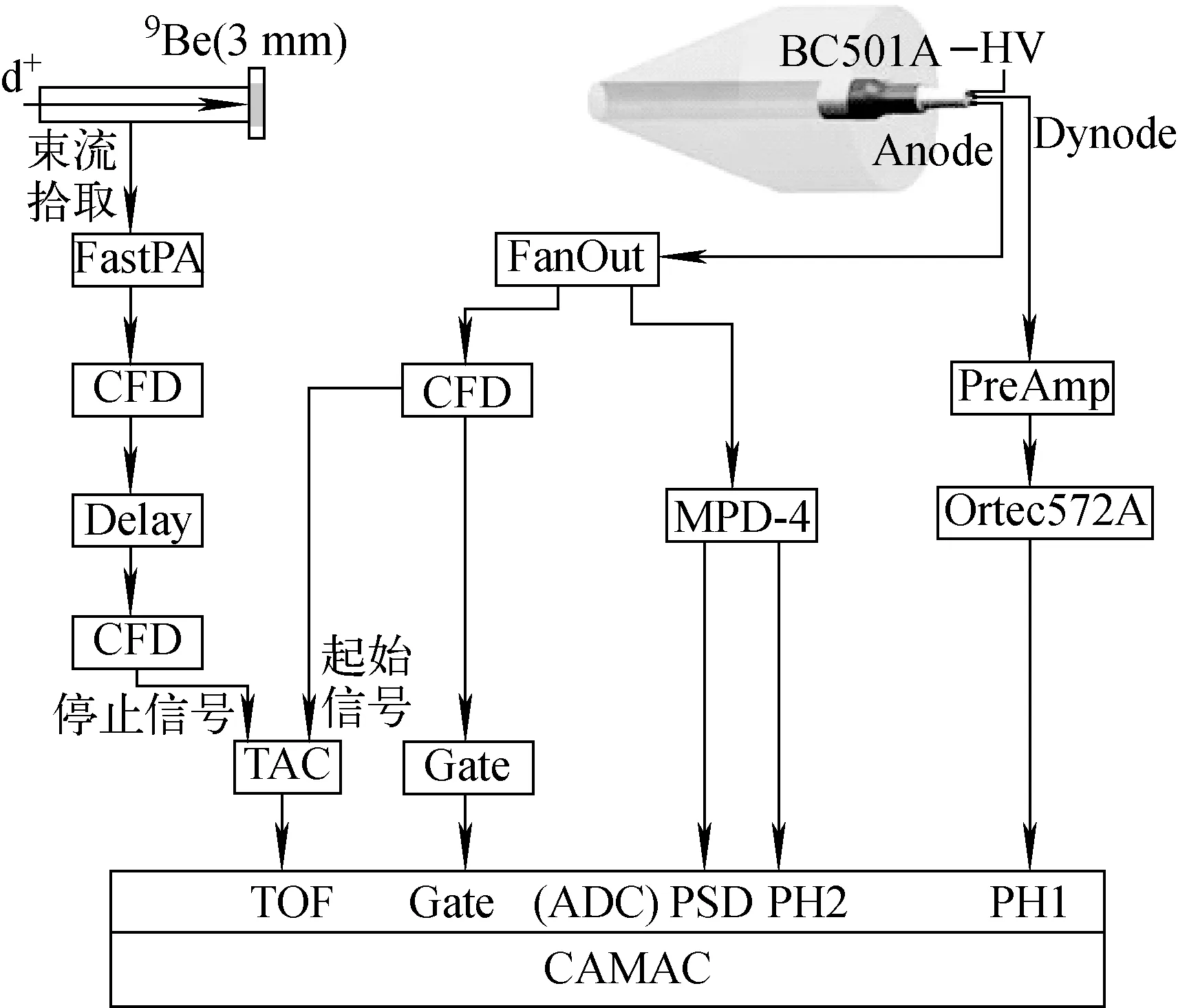
图1 实验布局及电子学示意图Fig.1 Experimental arrangement and electronic setup

实验是在中国原子能科学研究院计量测试部的5SDH-2串列加速器上进行的。使用2.5 MeV的氘束轰击3.0 mm厚的9Be靶，产生能量低于6.85 MeV的白光中子。实验中，脉冲氘束频率4.0 MHz，脉冲宽度3.2 ns，平均流强约4 μA。使用Saint-Gobain生产的BC501A液体闪烁体探测器[3]，直径2.0 in(1 in=2.45 cm)，厚度2.0 in。闪烁体后端匹配Photonis生产的XP2020光电倍增管，光电倍增管配有Ortec公司的269分压电路。实验布局及电子学如图1所示。探测器位于束流0°角方向，探测器表面距离靶面3.65 m。探测器有两路输出信号，一路为倍增极(Dynode)，从分压电路中间一级引出，信号幅度正比于闪烁体的光输出；另一路信号为阳极(Anode)，从分压电路的最后一级引出，信号上升时间小于6 ns，信号积分电荷量正比于闪烁体的光输出。Dynode信号经过前置放大器PreAmp进入主放大器(Ortec572A)[4]，主放大器的输出信号代表脉冲高度(PH1)，PH1信号接入CAMAC数据获取系统的ADC(ps7164)，此线路即采用了传统电子学。Anode信号经线性扇出插件FanOut(ps744)一分为二，一路进入MPD-4中，另一路进入恒比定时器CFD(Ortec935)。MPD-4输出2路信号至ADC，一路为脉冲高度信号(PH2)，另一路为粒子甄别信号PSD，即新型电子学。CFD输出2路定时信号，其中一路进入门产生器Gate(Ortec-Co4020)作为ADC的触发信号，另一路与脉冲拾取信号符合，作为飞行时间信号TOF。TOF信号由时幅转换器TAC(Ortec567)输出，其中探测器的定时信号为起始信号，脉冲束的拾取信号经过快前置放大器FastPA(Ortec-vt120)放大和CFD定时之后进入TAC作为停止信号，TAC输出信号进入ADC。通过调节Gate宽度使同一事件的不同信号均在1个Gate内，保证数据的一致性，本次实验使用的Gate的宽度为8 μs。

2 数据分析与讨论

2.1 能量刻度

液体闪烁体探测器的能量刻度是测量光响应函数的基础。一般使用单能伽马射线源进行能量刻度，通过拟合脉冲高度谱(PH谱)中的康普顿边确定最大康普顿电子的能量与ADC道值之间的关系[5]。本实验使用的伽马射线源为137Cs和22Na，对应的伽马射线的能量为662、511、1 271 keV。为精确确定康普顿边的位置，

需使用蒙特卡罗程序模拟单能伽马射线在探测器中的能量沉积，并根据探测器的能量分辨率展宽模拟谱，然后使用模拟得到的能量沉积谱拟合实验测量的PH谱，从而确定能量与ADC道数(Chn)的关系(式(1))。液体闪烁体的能量分辨率公式如式(2)所示，其中Eee为等效电子能量，A、B、C为影响能量分辨率的参数：参数A与光在闪烁体中的分布和传输有关，B与光产生、衰减、光电过程有关，C与光电倍增管和电子倍增的噪声有关[6]。实验中所用的探测器的A、B、C分别为9.17%、10.36%、0.5%。

Eee=aChn+b

(1)

(2)

采用Geant4程序构建探测器的几何模型，包括BC501A液体闪烁体、探测器外壳、光导和光电倍增管端窗。程序中将伽马射线源简化为点源，距探测器表面20 cm，记录探测器液体闪烁体内的能量沉积。使用ROOT程序展宽模拟谱并与实验谱拟合，如图2所示。

图2 模拟谱与实验谱拟合结果Fig.2 Fitting result of simulation spectrum and experimental spectrum

分别拟合Ortec572A得到的PH谱和MPD-4得到的PH谱，得到两种放大器的能量刻度曲线，如图3所示。能量刻度结果列于表1。从刻度结果可见，Ortec572A和MPD-4得到的等效电子能量与ADC道数的线性关系较好，满足实验测量的需求。

2.2 源中子能量测量

对于动能在20 MeV以下的中子，不需考虑相对论效应，中子飞行时间tn与源中子能量En的关系如式(3)所示，其中，l为中子飞行的距离，mn为中子的静质量[7]。

图3 能量刻度曲线Fig.3 Curve of energy calibration

(3)

表1 能量刻度结果Table 1 Energy calibration result

在实验中，通常利用中子靶上产生的伽马射线到达探测器的时刻确定中子飞行时间的零点，此时tn包括两部分，一是伽马射线从靶到探测器所经历的时间tγ，由距离l和光速c确定；二是伽马射线与中子到达探测器时刻的差值tγ-n，可根据TOF谱时间刻度的结果得到。一般使用精密脉冲发生器刻度TOF谱中ADC道数和时间的关系。实验中TAC的量程为500 ns，精密脉冲发生器每隔40 ns产生1个信号，累计13个信号覆盖TAC的整个量程，如图4所示。时间刻度结果显示，TOF谱中的ADC道数与时间具有较好的线性关系，平均每道为0.117 ns。

由于中子产生和输运过程中均会产生伽马射线，因此需在TOF谱中去掉伽马射线的计数。实验中使用MPD-4的粒子甄别功能，将PSD和PH信号做成双维谱，可明显区分中子和伽马信号，如图5所示。

根据TOF谱刻度结果和式(3)可得到源中子的能谱。图6a为源中子的TOF谱，包括没有粒子甄别条件的原始谱和包含粒子甄别条件的净中子谱。图6b为通过净中子TOF谱得到的中子能谱，其中纵坐标计数的不确定度主要来源于统计不确定度；横坐标能量的不确定度主要来源于3.2 ns的脉冲束时间宽度，在1 MeV处约为2.5%，在6 MeV处约为6%。

图4 TAC时间刻度谱Fig.4 TAC time calibration spectrum

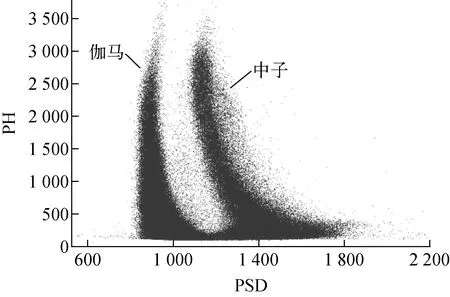
图5 粒子甄别二维谱Fig.5 2D spectrum of particle discrimination

2.3 光响应函数计算

得到源中子能谱后，即可挑选不同能点得到单能中子的PH谱。根据PH谱上的能量边界和能量刻度的结果可得到该中子能量En对应的等效电子能量Eee。为保证PH谱有足够的统计，选取中子能量时增加了±2%的区间。选取1.78 MeV到6.41 MeV能区中的7个能点，分别得到Ortec572A和MPD-4的PH谱，如图7所示。

图6 源中子飞行时间谱(a)和源中子能谱(b)Fig.6 TOF spectrum of source neutron (a) and energy spectrum of source neutron (b)

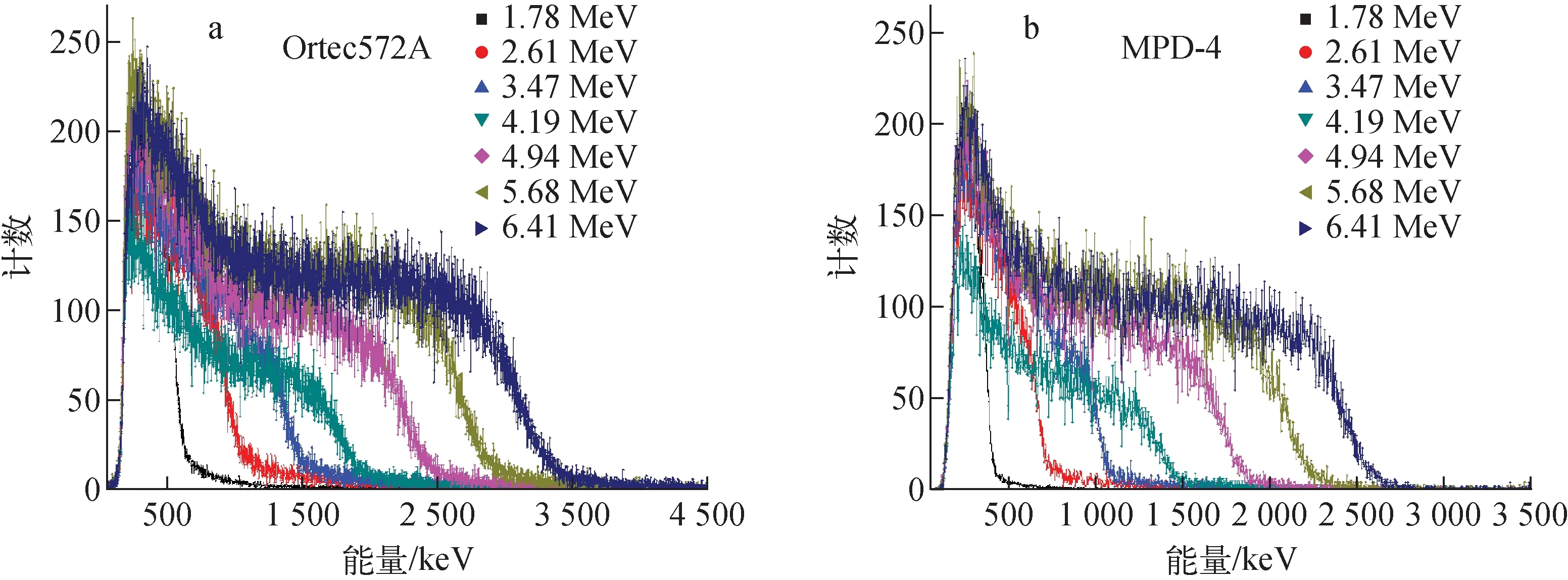
图7 Ortec572A(a)和MPD-4(b)的PH谱Fig.7 PH spectra of Ortec572A (a) and MPD-4 (b)

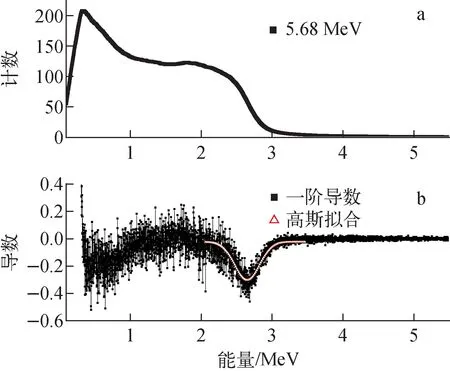
图8 5.68 MeV中子的PH谱(a)和PH谱的一阶导数(b)Fig.8 PH spectrum of 5.68 MeV neutron (a) and the first derivative of PH spectrum (b)

在单能中子的PH谱中，PH谱高能段的边界即为反冲质子的最大能量，代表入射中子的能量。实验中由于能量分辨率等因素，PH谱的边界具有一定的展宽。确定反冲质子边可采用蒙特卡罗模拟的方法，也可如Kornilov等[8]所述，通过PH谱的一阶导数得到。本次实验采用一阶导数的方法得到反冲质子边，以Ortec572A测得的5.68 MeV中子的PH谱(图8a)为例，PH谱的一阶导数如图8b所示，对一阶导数在质子边附近高斯拟合即可得到质子边的道数。

图9 中子光响应函数测量结果Fig.9 Measurement results of neutron light output response

分别得到不同能量中子的PH谱中质子边的值，即可给出相应的光响应函数曲线，如图9所示。图9中横坐标为入射中子能量，其不确定度与图7b中的能量不确定度一致，主要来源于脉冲束的时间宽度；纵坐标即为质子边对应的等效电子能量，即光响应，其不确定度约5%，主要来源于质子边道数的不确定度和伽马刻度的不确定度。图9中Previous代表实验室曾经使用的BC501A的光响应函数，NE213为Lee等[9]测量得到的NE213的光响应函数。可见通过Ortec572A测到的光响应曲线与已有的光响应函数在不确定度范围内较一致，而MPD-4得到的光响应函数曲线明显偏低。

为了解MPD-4得到的光响应函数较其他数据偏低的原因，开展了对MPD-4电子学的研究。Ruben等[10]指出，为减少电子学死时间和提高能量分辨率，MPD-4使用新的方法得到信号的能量信息。其将PMT的阳极信号进行了6阶梯形滤波，然后对成形后的信号进行电荷积分作为能量信号。但为节省电子学信号处理的时间，电荷积分的时间宽度只有20 ns，不能完全覆盖探测器的信号，对获取能量信息造成一定的影响。图10引用自文献[10]，给出了不同粒子的原始信号和经过MPD-4成形后的信号。对于同一类型的粒子，不完全的积分仅会改变能量刻度的结果。但当入射粒子种类不同时，由于不同粒子的探测器信号的慢成分比例不同，不完全的积分导致不同粒子损失的能量比例不同，此时不同粒子的能量刻度会有不同比例的改变。以中子和伽马射线为例，中子(质子)信号的慢成分比例远大于伽马(电子)信号，不完全的积分使中子信号损失更多的能量，从而表现为对应的等效电子能量降低，即光响应降低，这与实验结果一致。相比于MPD-4，传统的前置放大器和Ortec572A放大器的成形时间为1 μs左右，可覆盖完整的信号，因此不会改变探测器固有的光响应函数。需指出，在实验组此前开展的实验中，也曾使用波形采集或QDC对探测器阳极信号进行电荷积分得到BC501A的反冲质子谱，实验中探测器信号宽度约120 ns，QDC的积分时间为200 ns。在这些实验的数据处理过程中，可使用已有的光响应函数(图9中的Previous)计算出合理的结果(如入射中子能量等)，因此认为使用探测器的Anode信号通过完整的电荷积分得到的光响应函数与使用Ortec572A类型的主放大器得到的光响应函数是一致的。

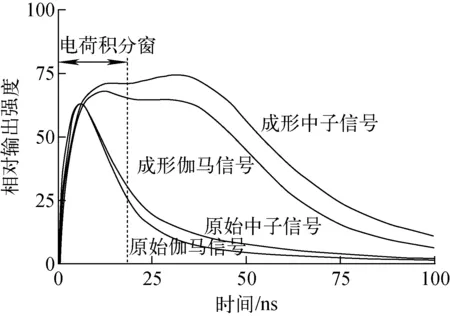
图10 中子和伽马的原始信号及成形信号[10]Fig.10 Original and shaped signals of neutron and gamma[10]

3 结论

对MPD-4这种新型的高集成度电子学插件开展了BC501A型探测器的光响应函数实验研究，发现与传统电子学相比，光响应函数有明显的差异。分析认为差异的原因主要是放大器成形时间和积分时间不同，因此，对于采用此种电子学插件的中子探测系统，需要对中子的光响应函数进行测量，才能得到可靠的结果。

感谢中国原子能科学研究院计量测试部中子组的王志强研究员、刘毅娜副研究员和骆海龙工程师运行5SDH-2串列加速器，并提供了较好的脉冲中子束流。