基于变增益模糊PID控制的移动机器人轨迹跟踪

赵会超，师五喜

（天津工业大学 电气工程与自动化学院，天津300387）

轮式移动机器人是一种典型的非完整性系统，具有广泛的应用前景，机器人领域的变化趋势由在生产线固定的机械手向能做更复杂任务的自主移动机器人过渡，比如救援、军事行动以及日常生活服务等，移动机器人控制的一个主要问题是轨迹跟踪控制，然而描述轨迹跟踪的跟踪误差系统往往是一个耦合非线性系统，使得该问题的解决变得复杂，在实际应用中，需要充分考虑移动机器人的模型不确定性等问题，目前移动机器人轨迹跟踪的方法主要有智能控制方法[1-3]、反步控制方法[4-5]、滑模控制方法[6-10]、自适应控制方法[11-14]等。文献[1]采用了基于模糊神经网络的控制方法，保证机器人对参考轨迹的实际跟踪，文献[2]在文献[1]的基础上提出了一种运动学控制器与自适应动态递归模糊神经滑模控制器相结合的控制结构，使不确定性估计误差有效减小，但以上控制器的设计比较复杂，在实际应用中不宜实现，文献[4]提出一种基于扰动补偿的反演控制方法，有效抑制了在外部扰动下轮式移动机器人轨迹跟踪容易出现速度跳变的问题，文献[9]提出一种基于滑模控制的移动机器人轨迹跟踪控制方法，然而滑模控制中由于惯性、滞后等因素，不可避免地存在抖振现象，文献[10]在文献[9]基础上引入新型加权增益趋近律，在积分项中引入负的加权值，减少滑模控制固有的抖振问题，但改进的滑模控制方法影响了系统的鲁棒性且无法完全解决抖振问题，文献[12]针对纵向滑动参数未知的轮式移动机器人的轨迹跟踪问题，提出一种自适应跟踪控制策略，利用两个未知参数来描述移动机器人左右轮的纵向打滑程度，建立了产生纵向滑动的差分驱动轮式移动机器人的运动学模型，文献[13]针对机器人轨迹跟踪控制品质受到参数不确定性影响的问题，设计了一种自适应非光滑控制，但该方法不适用于传统的稳定性分析和设计工具，文献[15]基于动力学模型设计了模糊PD控制器，实现了机器人跟踪控制，文献[16]在文献[15]的基础上，将模糊PI控制器和模糊ID控制器结合，提高了控制精度，但文献[16]提出的二维PID模糊控制器的结构复杂，模糊控制方法实时性不高。

本文提出了一种变增益的模糊PID控制方法，将常规PID分为PI和PD的组合，控制器的输出可以转化为误差和误差变化率的和，然后设计模糊控制器的增益，该增益根据误差的变化自适应调节，最终实现移动机器人的轨迹跟踪，本文方法优化了控制器的输出，结构简单，控制精度高，实验结果验证了所提算法的有效性。

1 系统模型

1.1 移动机器人的运动学模型

本文研究的机器人结构如图1所示。图中OXY为全局平面坐标系，表示移动机器人在空间平面的位置，OcXcYc为机器人局部坐标系，Oc表示机器人的几何中心，v为机器人前进线速度，方向垂直于机器人轮轴，w为机器人角速度，θ为机器人运动方向与X轴夹角，P表示机器人质心位置，图中2b表示机器人两车轮之间的距离，2r为车轮直径，Oc与p之间的距离记为d。

图1 轮式移动机器人模型Fig.1 Wheeled mobile robot model

假设移动机器人在理想条件下运动，即满足机器人纯滚动无滑动条件时，移动机器人运动时满足公式：

引入机器人运动学模型控制量z，将移动机器人模型表示如下[17]：

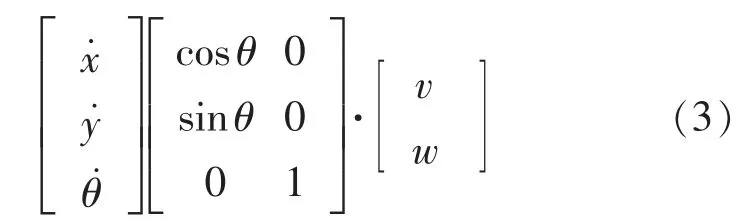
式中：（x，y，θ）为移动机器人实际位姿。

1.2 移动机器人的动力学模型

移动机器人系统动力学模型表示为[18-19]

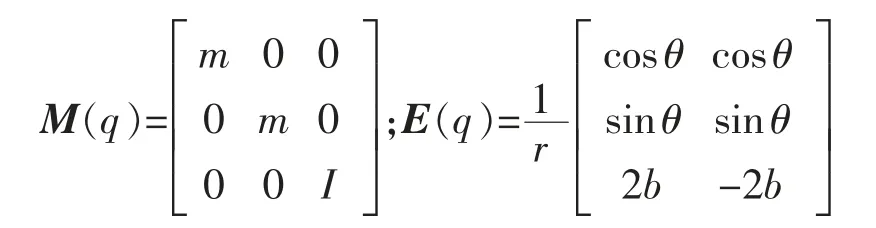
式中：m为机器人的质量；I为机器人的总转动惯量，移动机器人动力学模型控制输入为机器人驱动轮力矩状态向量

2 移动机器人轨迹跟踪控制器设计

本文先基于移动机器人运动学模型，设计辅助运动控制律，然后将移动机器人的线速度和角速度的辅助速度作为输入，基于动力学模型设计模糊PID控制算法，使移动机器人的实际速度渐近收敛到辅助速度，最终实现移动机器人的轨迹跟踪。

2.1 移动机器人运动控制律设计

假设移动机器人参考轨迹如下：

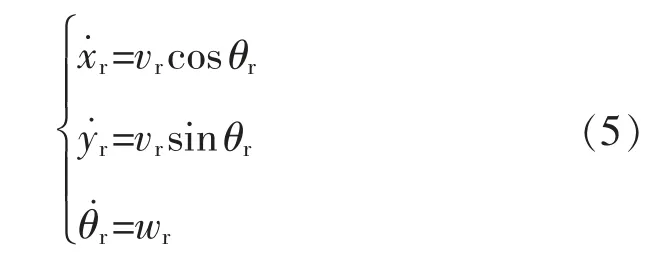
式中：vr为移动机器人期望线速度；wr为期望角速度；（xr，yr，θr）为移动机器人期望位姿。

定义轨迹误差为

对式（6）求导可得：

设计如下的辅助运动学控制律[20]：

式中：vc为移动机器人辅助线速度；wc为辅助角速度；k1、k2、k3为辅助运动控制律参数，且k1、k2、k3>0。在辅助运动控制律作用下，移动机器人的辅助速度渐近收敛到期望速度

2.2 模糊PID控制器设计

式中：zc和z分别是移动机器人的辅助速度和实际速度，令线速度的误差ve=e1（t），角速度的误差we=e2（t），分别对ei（t）（i=1，2）设计PID控制算法。常规PID的控制规律为

本文将常规PID中的比例环节分为两部分，分别与积分环节、微分环节结合，这样将常规PID控制变为PI控制与PD控制的组合：

①PI控制器的输出为

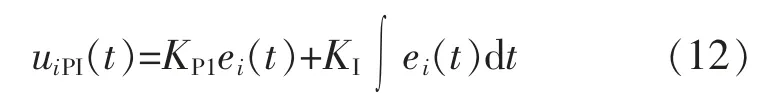
式中：ei（t）=ri（t）-yi（t）为误差信号；uiPI（t）为控制器的输出；KP1和KI为比例系数和积分系数。

将上式转换为速度形式为：

在频域中转化，并利用后向差分法代入，当T>0时，利用z 反变换得到：

令KP1=GP1，KI=GI，式（14）等价于：

由式（15）设计PI控制器，输入变量是误差ei（kT）和误差变化率eci（kT），输出变量为控制量uiPI；PI控制器的输出由下式给出：

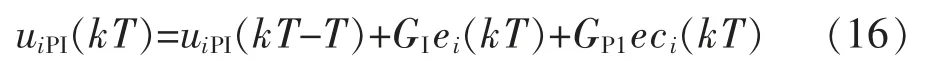
②PD控制器的输出为

式中：ei（t）=ri（t）-yi（t）是误差信号；uiPD（t）是控制器的输出；KP2和KD分别是比例系数和微分系数。

式（17）在频域中转换，并利用后向差分法代入，当T>0时，利用z 反变换得到：

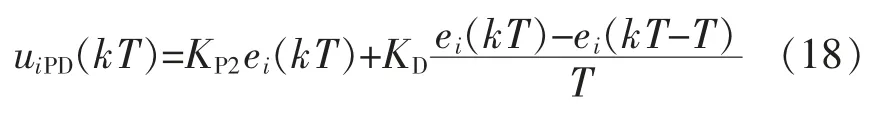
令KP2=GP2，KD=GD，式（18）等价于

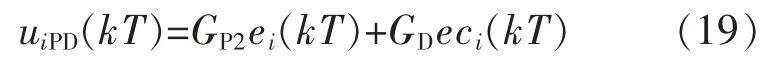
结合式（16）和式（19），式（11）转化为

令K1=GI+GP2，K2=GD+GP1，代入式（20）可得PID控制器的总输出为

由式（21）设计模糊PID控制算法。

2.3 模糊化和模糊控制规则

2.3.1 输入变量及其模糊化

模糊控制器的输入变量为误差ei（kT）和误差变化率eci（kT），量化后的论域取为[-L，L]，输入变量在其相应的论域上定义为参考模糊集：负（N）、正（P），相应的隶属度函数如图2所示。

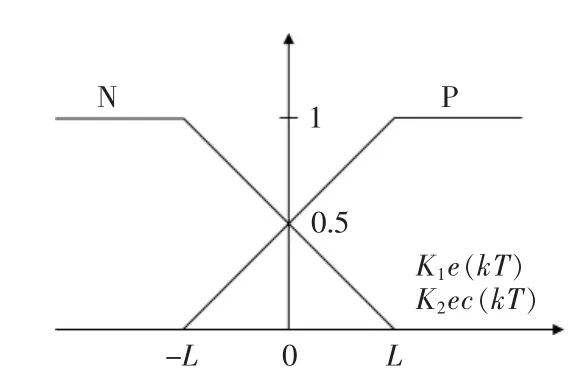
图2 输入的隶属度函数Fig.2 Input membership functions

2.3.2 输出变量及其模糊化

模糊控制器的输出变量是Δu1，输出变量在其相应的论域上定义为3个参考模糊集，分别是负（N）、零（Z）、正（P），-L，0，L分别是其各自隶属度函数的中心值，相应的隶属度函数如图3所示。

输出的隶属度函数表达式为

输出u1的表达式为

式中：Gu1是输出变量Δu1的量化因子。

2.3.3 模糊控制规则

由模糊控制器的结构，指定的输入是K1ei（kT）和K2eci（kT），输出量是Δu1，基于模糊化中描述的输入和输出隶属度数，模糊控制器的模糊控制规则的数量为4，控制规则如下：

R1：if K1ei（kT）is N AND K2eci（kT）is N THEN Δu1is N

R2：if K1ei（kT）is N AND K2eci（kT）is P THEN Δu1is Z

R3：if K1ei（kT）is P AND K2eci（kT）is N THEN Δu1is Z

R4：if K1ei（kT）is P AND K2eci（kT）is P THEN Δu1is P

2.3.4 精确化计算

“重心法”用于计算模糊PID的控制作用，模糊控制器基于当前的精确化输出如下：

式中：μr是控制规则中的隶属度值；Δu是输出，根据模糊推理方法可求出个区域相应的激活度，模糊控制器的输入组合（IC）值的区域如图4所示。

图4 模糊PID分量输入组合的区域Fig.4 Fuzzy PID component input combination area

模糊控制器的区域可以分解为12个不同的区域（IC）。Δu的结果是在每个隶属度区域应用解模糊算法获得，将隶属度数值带入，整理得到：

综上，由辅助运动学控制器和基于动力学模型的模糊PID控制器，可得系统控制器总框图如图5所示。

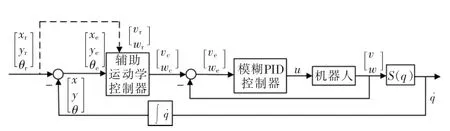
图5 机器人闭环控制系统总框图Fig.5 Total block diagram of the robot closed-loop control system

3 实验

为验证控制方法的有效性，在平台Qbot2 上进行实验，实验目的是使移动机器人跟踪给定的参考轨迹，参考轨迹为一个半径1 m的圆形：xr=sint，yr=-cos t，θ=t，实验环境包括：1台Qbot2机器人，6个OptiTrack 摄像头，1台PC主机，PC机是系统的控制中心，安装有实验所需的控制软件与摄像机跟踪处理软件，PC机控制软件集成了Matlab/Simulink模块和无线通信模块。PC机与Qbot2 通过无线模块进行通信，PC机和OptiTrack定位系统通过USB2.0连接，OptiTrack定位系统实时跟踪Qbot2位置信息并在PC机上显示。

移动机器人在平面上的运行轨迹如图6所示。

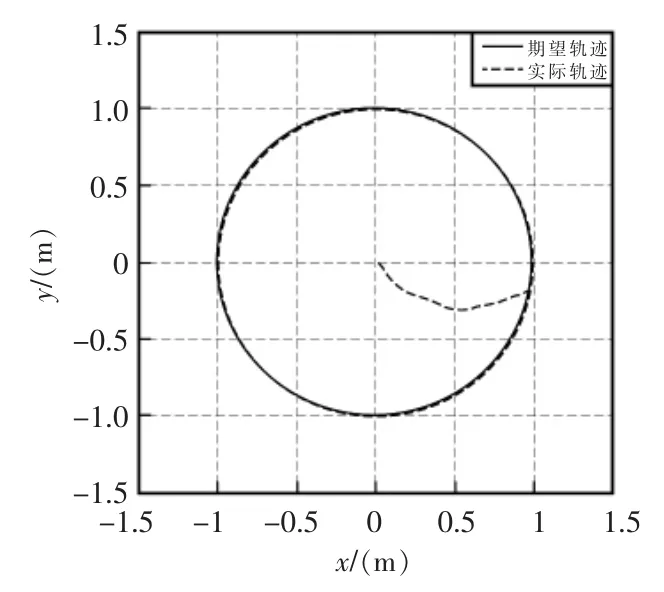
图6 移动机器人运动轨迹图Fig.6 Mobile robot motion trajectory

移动机器人速度曲线如图7所示。

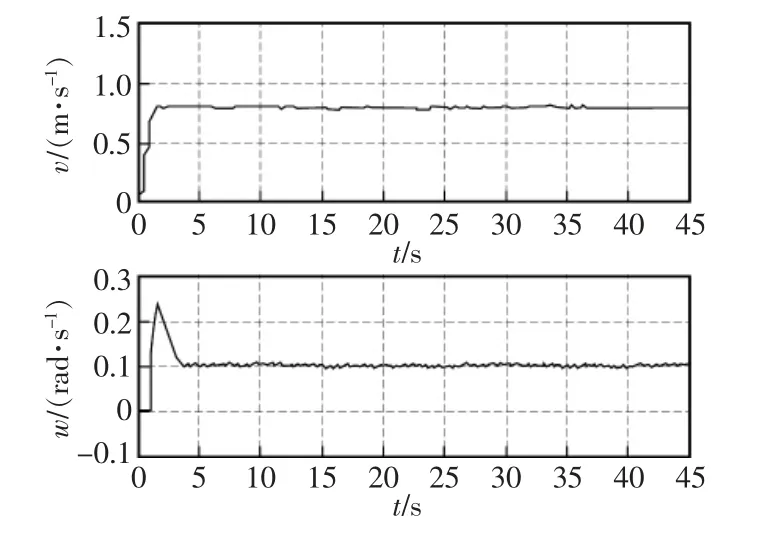
图7 移动机器人线速度和角速度曲线Fig.7 Mobile robot linear velocity and angular velocity curve

移动机器人误差曲线如图8所示。

4 结语

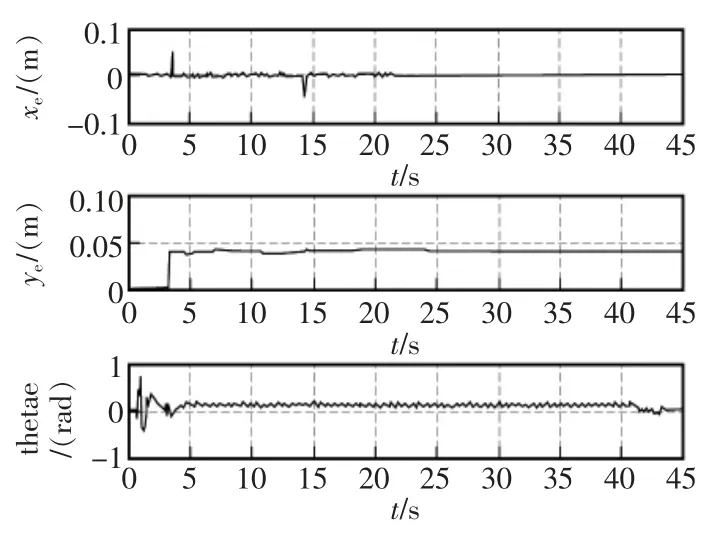
图8 模糊PID 误差曲线图Fig.8 Fuzzy PID error graph

本文针对移动机器人轨迹跟踪问题，提出了一种基于变增益的模糊PID控制方法，首先分析了移动机器人的运动学模型和动力学模型，进而建立了轨迹跟踪控制系统模型，然后设计了结构简单、运算较快的模糊PID控制器，从实验结果可以看出，系统的响应速度快、调节精度提高，稳态性能好，这是传统的PID控制难以实现的，能较明显地提高控制效果，发挥了传统控制与模糊控制的长处，具有较强的实际意义。