钢构件在压弯扭组合变形模式下的变形探究
杨钊煜 梅宇东 王孟然 胡楷羽 谭晓华
(天津职业技术师范大学 天津 300222)
在工程实际当中,钢构件受到轴向力、弯矩与扭矩共同作用的情况非常普遍,探究复杂变形模式下构件的应力应变状态对于机械工程、土木工程等领域有非常重要的意义。现阶段通过利用各种仿真软件,可以对一些特殊环境下构件的应力应变状态进行分析,例如蒋豹等人探究了阶梯轴在压弯扭组合变形模式下的应力集中问题;杜赞华探究了钢筋混凝土在复杂变形模式下的极限扭矩,韩庆华等人提出了压弯扭共同作用下闭口截面构件弯矩作用平面内极限承载力计算公式并通过大量数值模拟实验进行了验证。但现有文献对于钢构件在压弯扭组合变形模式下的变形缺少研究。
文中通过有限元分析,研究悬臂梁式钢结构在压弯扭组合变形条件下的应变量,并将其与单一载荷作用下的应变量进行对比,为复杂情况下的钢构件变形分析方法提供有效支撑。
1 力学中的叠加原理
叠加原理又称力作用的独立性原理。在小变形和线弹性的情况下,构件受荷载作用所产生的效应与荷载呈线性变化,即多个荷载同时作用所产生的效应等于各个荷载单独作用所产生的效应之总和。这样,在分析问题和解决问题时,可以把复杂的研究问题,分解为若干个简单问题,在分析的基础上分别解决各个简单问题,然后将各个简单问题统一到复杂的研究问题上来,使复杂问题得到解决。这是固体力学分析求解中的重要原理之一。
根据叠加原理,空心矩形截面悬臂梁在自由端同时受到轴向压力、横向集中力和扭矩作用时,如图1所示,其横截面内任一点的应变可以表示成:


图1:压弯扭组合变形悬臂梁示意图
2 压弯扭组合变形模式下的变形
本文采用ABAQUS有限元软件分析钢构件的组合变形。模型横截面为中空的正方形,尺寸为50mm×50mm×500mm,中空部分尺寸40mm×40mm×500mm。材料选用45号钢,其杨氏模量为200GPa,泊松比为0.3。在软件中设定材料属性后设置约束类型及载荷形式。本次实验中采用悬臂梁的约束类型,即一端固定、一端施加载荷。
在构件右端的截面上选取中心点为耦合点,将整个右端截面与这一点耦合,使整个截面的受力状态与这一点的受力状态相同。在构件右端的耦合点上同时施加三种载荷,如图1所示。z轴方向压力FZ大小为2500N,y轴方向的压力Fy大小为2500N,绕z轴顺时针方向的扭矩M大小为750000N·mm。对构件模型进行网格划分后,获得主应变仿真结果。从图2可以看出,该构件的最大应变值发生在固定端附近,且上半部分应变明显高于下半部分应变,总体呈非均匀非线性状态分布。

图2:组合变形主应变云图
为进一步分析应变数值随着时间的变化规律,本文选取构件右端左上角一点作为参考点,如图2所示。对参考点在X轴、Y轴、Z轴三个方向的应变进行分析。绘制参考点应变曲线,如图3所示。通过提取图中曲线数据,可以得到各个方向应变的具体数值。从以上结果可以看出,各应变分量随时间线性变化,其中11线性增加,22和33线性减小。

图3:参考点应变曲线
3 单一载荷作用下的基本变形
采用相同的钢构件及相同的约束条件重新建立有限元模型,将以上三种载荷分别单独施加在构件相同位置,对三种模型进行仿真计算后获得主应变结果如图4所示。

图4:基本变形主应变云图(a)单轴压缩变形(b)弯曲变形(c)扭转变形
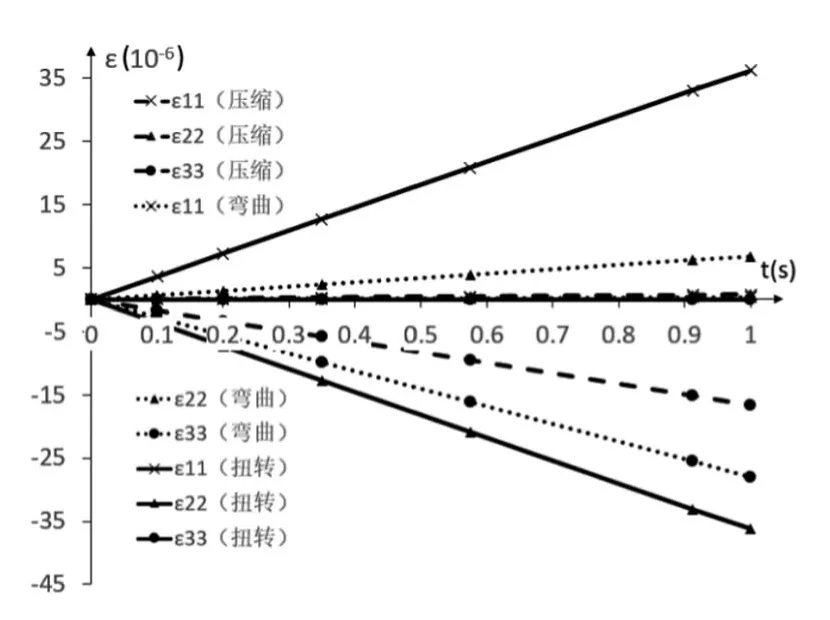
图5:参考点应变曲线

图6:三种应变叠加值与组合应变值的偏差
4 结论
本文通过有限元软件计算了空心钢构件在压弯扭组合变形模式下的变形量,分析其随着时间的变化规律。并将单一拉伸、弯曲、扭转情况下的应变数据进行叠加,与组合变形条件下的应变数值进行比较。可以看到在满足线弹性、小变形的理想条件下,钢构件在拉弯扭组合变形模式下的应变量与三种载荷单独施加所产生的应变量的数值基本相同,最大偏差为3.63798×10-12,进一步验证了力学中的叠加原理。
致谢:
感谢天津市大创项目(编号:201910066042)对本文工作的支持。

