考虑空气密度变化的风电机组转矩控制算法研究

张国强，田宏哲，杨政厚

（北京华能新锐控制技术有限公司，北京 102209）

0 引言

风能作为一种绿色清洁能源，风力发电发展迅速。随着技术进步，对风电机组控制系统要求越来越高，控制趋向多元化、精细化、智能化方向。为了提高机组发电效率，提升在役风电场发电量，最大风能捕获控制算法成为了研究热点[1]～[3]。

风电机组发电功率直接受到风速和环境参数的影响，许多专家学者针对此问题提出了解决方法。文献[4]考虑环境温度和湿度，提出了功率反馈的最大风能捕获控制PSF 算法，得到较好的仿真测试结果。文献[5]提出了在空气密度降低情况下的功率自适应的优化方法，并在MATLAB 平台上搭建直驱机组模型进行仿真，优化方案在风速阶跃阶段效果较好。但是仅做了恒定风速的仿真，未考虑机组的非线性气动特性。文献[6]分析了影响空气密度的环境因素，提出了自适应空气密度变化的控制算法，并结合实际机组进行验证。但测试过程中未考虑两台机组自身的性能差异导致的发电功率不同。

本文从风电机组基本发电原理出发，分析额定风速以下最优转矩控制与空气密度的关系，提出了空气密度变化修正的最优转矩控制方法。结合吉林省某风电场1年的实际测量数据，分析了风电场环境下空气密度变化规律。最后，基于Bladed 软件平台，在平均风速6 m/s 湍流风况下，进行了5 组仿真试验，验证了所提出的修正算法的功率提升效果。

1 空气密度与风电机组转矩控制的关系

在实际运行中，风电机组输出功率的大小直接受到风的影响。通常只关注风速和风向，忽略了空气密度变化的影响，本文从理论角度，结合兆瓦级双馈型风电机组，分析了空气密度对风电机组功率的影响。

风电机组的输出功率与风速的关系为

式中：Cp为功率系数，表征风电机组的风能捕获效率；ρ 为空气密度；A 为风轮的扫略面积 A=πR2；V 为来流风速。

风电机组的输出功率与空气密度大小直接相关，图1 为同一台风电机组在不同的空气密度下的风功率曲线。

风电厂商一般提供标准空气密度（1.225 kg/m3）下的功率曲线，而风电场的实际空气密度并不是标准条件下的密度，因此，在进行运行数据拟合功率曲线时须要依据现场的空气密度进行修正[7]。

图1 不同空气密度下的风功率曲线Fig.1 Wind-power curve in different air density

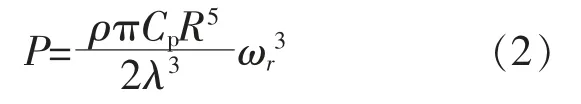
式中：ωr为风轮转速。

风电机组 Cp是 V，ωr和桨距角 β 3 个变量的函数。在额定风速以下，通常β 保持在最佳角度不改变，此时Cp和λ 的关系曲线如图2 所示。由图2 可知，在额定风速以下功率系数为λ 的单值凸函数，即在运行区间内存在一个最大的Cp值，此时，对应叶尖速比λopt称为最优λ。最大风能捕获原理就是通过控制发电机转速，在不同的风速下使 λ 保持在 λopt，从而保证 Cp最大。

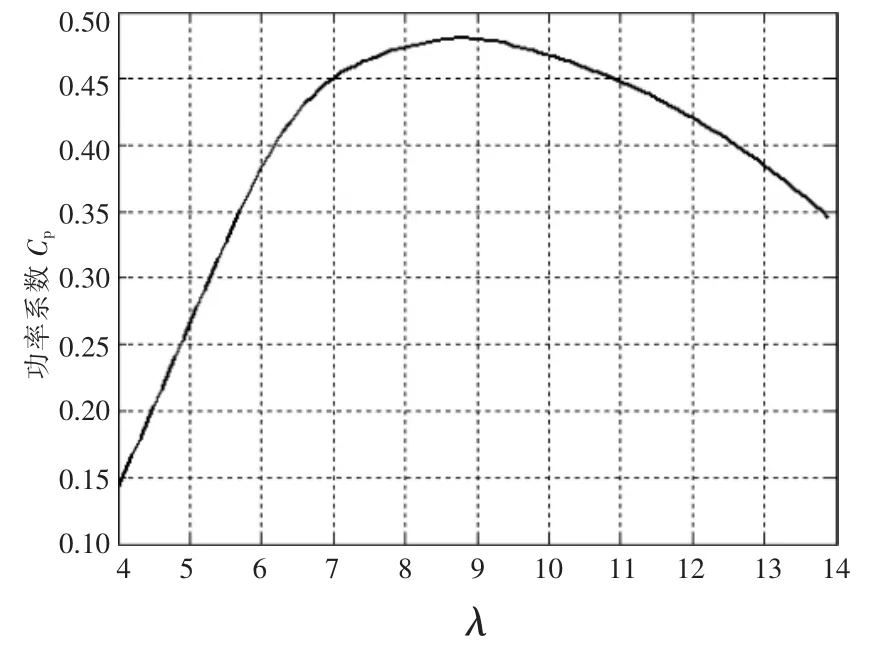
图2 β=0 时功率系数与叶尖速比的关系Fig.2 Relationship between power factor and tip speed ratio when β=0

风电机组发电系统属于旋转机械，其输出功率也可以表示为转速和转矩的乘积，忽略机械损失和转化效率，可得：

式中：Tr为风轮系统的转矩；Tg，ωg分别为发电机的转矩和转速值，其中 ωg=Gωr，G 为齿轮箱的传动比。

联立式（2）和式（3），得到：

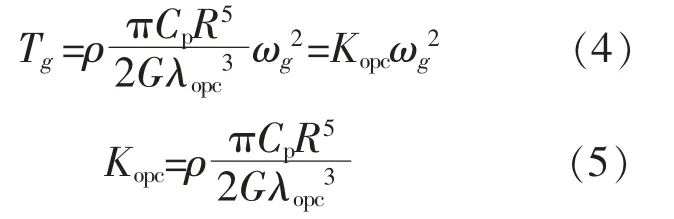
式中：Kopc为控制参数。

在额定风速以下，双馈发电机转速控制是通过调节电机电磁转矩实现的，因此，只要控制发电机转矩和转速使其满足式（4）的关系，就可以保证风电机组获得最大的风能捕获效率。Kopc与ρ 呈正相关关系，现场的空气密度实时变化，为保证获得最大功率，须要根据实际空气密度对控制系统进行优化。

2 现场数据分析

根据式（1）可知，空气密度变化对风电机组输出功率有很大的影响。本文选取吉林省某风电场2017-12-01-2018-11-30日测风塔处的空气密度数据，分析了风电场环境下空气密度的变化规律。数据间隔15 min，得到的原始数据如图3 所示。

图3 空气密度原始数据曲线Fig.3 Curve of air density raw data

由于原始数据存在很多错误点，须对原始数据进行筛选修正及分析统计。

（1）数据筛选修正

风电场现场环境恶劣，由于传感器故障、数据通讯存储错误等原因造成采集的数据不真实。在进行数据分析前，须要进行筛选及修正。

限值判断：结合空气密度实际物理意义，将图3 中数值为0 和小于0.8 的数据判断为错误点。

变化率判断： 空气密度为大气环境的一项表征参数，是连续缓变的过程，若相邻采样点数据发生突变（本文设置为0.12），判断为变化率超限错误点。

修正方法：对原始错误点进行标记。本文采用错误数据点前一天（96 点）平均值替换错误数据。

（2）数据处理

根据修正后的数据，选取其中无错误的3 d时间段的数据，得到图4 所示的空气密度变化曲线。分析空气密度的每日变化规律，分别计算空气密度的日平均值、月平均值和年平均值，并统计365 个日平均值的最大值和最小值，计算结果如图5 所示。

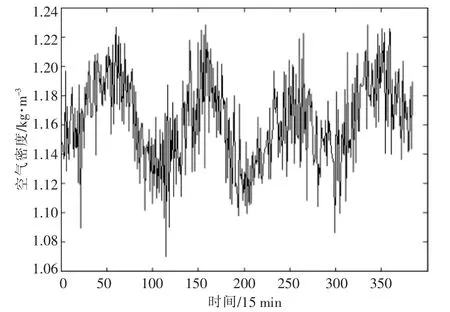
图4 空气密度3 d 数据Fig.4 Air density data in 3 days

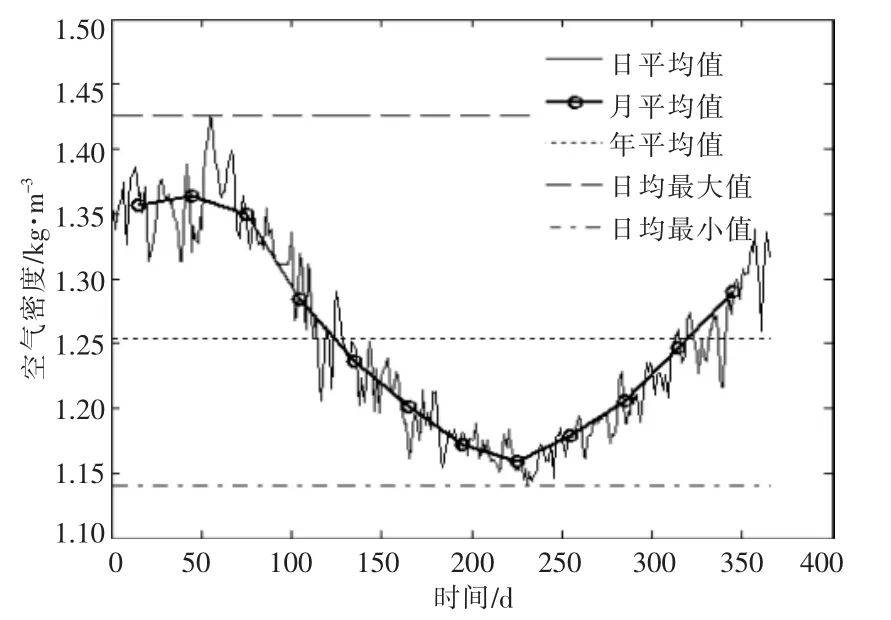
图5 空气密度日均值、月均值和年均值分布Fig.5 Distribution of air density about daily average，monthly mean and annual mean

（3）结果分析

由图4 可知，空气密度整体趋势呈现以日为周期的变化规律，夜晚空气密度大于白天，每个时刻的值在一定范围内进行波动，每日的最大值和最小值约相差0.1 kg/m3。

由图5 可知，12 个月空气密度均值在年度区间内呈季节性变化，冬季大于夏季，整体趋势近似按照正弦规律变化。365 个日均值不是一条平滑的曲线，在一定范围内有较大波动。所研究风电场空气密度年平均值为1.253 3 kg/m3，日均值的最大值为1.425 4 kg/m3，日均值最小值为1.140 4 kg/m3，最大值与最小值相差25%，日均空气密度在冬季和夏季变化很大。

3 考虑空气密度变化的转矩控制修正

由式（5）可知 Kopt与 ρ 成正比关系，实际机组控制系统中采用恒定值作为控制参考，未考虑现场空气密度的季节性变化，考虑空气密度修正后式（5）为

式中：ρ0和Kopt-0分别为标准空气密度及其对应的最优转矩系数；ρact和Kopt-act分别为现场实际空气密度和修正后的最优转矩系数。

根据式（6），在传统最优转矩PID 控制算法基础上，增加空气密度修正系数，控制流程如图6所示。

图6 带有空气密度修正的转矩控制算法Fig.6 Torque control algorithm with air density correction

本文基于Bladed 软件平台，在1.5 MW 双馈风电机组模型基础上，进行了空气密度修正转矩控制算法仿真，设计了5 组对照实验。其中：T1，T2 两组空气密度设置为风电场日均最大值，T1组转矩控制算法未修正，T2 组采用转矩修正算法；T3，T4 两组空气密度设置为日均最小值，T3组转矩控制算法未修正，T4 组采用转矩修正算法；T5 组为对照组，空气密度和转矩系数皆采用标准值。

仿真具体参数见表1。风速设置为平均值6 m/s 的Kalman 湍流风模型，仿真时间为600 s，其他模型参数和控制参数均不作改变。

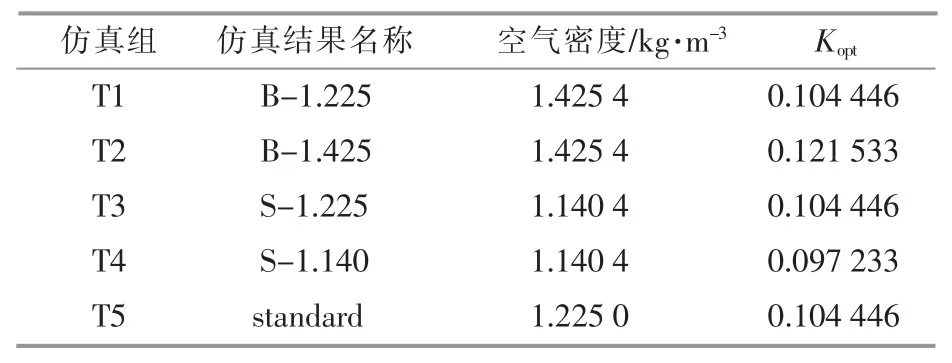
表1 仿真实验组设置参数表Table 1 Parameter of simulation experiment group setting

4 仿真结果分析

对比5 组仿真结果，分别计算发电功率、发电机转矩和发电机转速的均值和标准差，计算结果如表2 所示。

根据 IEC 标准的建议[8]，采用 Bins 法对功率和风速数据进行分析，在运行范围内将风速分为间隔0.5 m/s 的区间，在每个区间内分别统计风速及功率的平均值，得到如图7 所示风功率曲线。

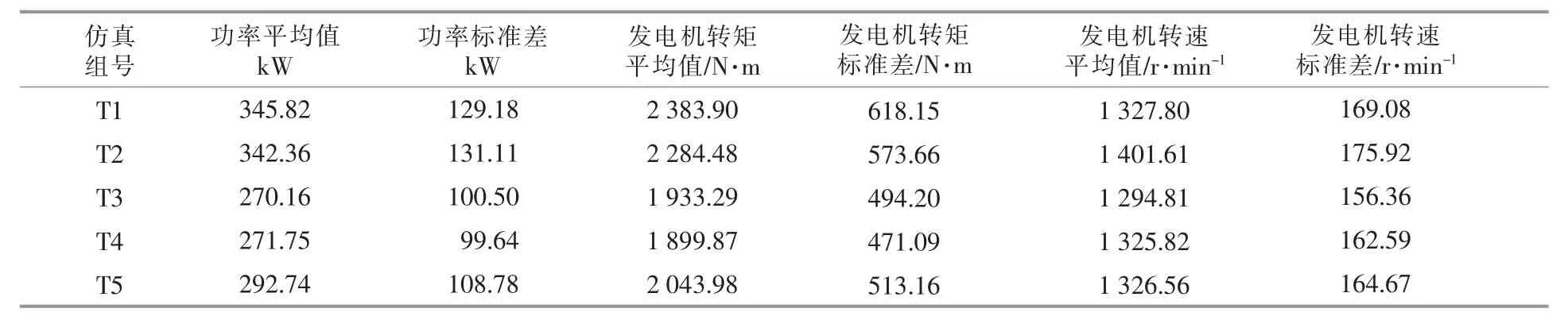
表2 5 组湍流风况仿真结果Table 2 Result of five simulation experiment in turbulent wind

图7 仿真结果的统计风功率曲线Fig.7 Wind-power curve of the simulation result

由图7 可知：

（1）对比实验组 T1，T3 和 T5，空气密度是直接影响机组输出功率的因素，空气密度越大，相同风速下机组的发电功率越大；

（2）对比 T1 和 T2，空气密度相差 16.36%，平均发电功率经过空气密度修正后降低了1.00%；对比T3 和T4，空气密度相差6.91%，修正后平均功率提升了0.59%。在同一空气密度下，经过空气密度修正转矩控制算法，对机组功率输出影响不大；

（3）对比 T1 和 T2 的结果，发电机转矩和转速变化分别为4.20%和5.56%；对比T3 和T4 的结果，发电机转矩和转速变化分别为1.73%和2.39%。空气密度修正后发电机转矩和转速将会产生较大的变化，影响风电机组载荷。

针对空气密度修正后，风电机组功率改变较小的结果，进一步进行仿真实验研究。设计两组平均风速为6 m/s 恒定风，空气密度设定为1.425 4 kg/m3仿真实验，其中仿真C1 不进行修正，仿真C2 根据空气密度对Kopt 进行修正，仿真得到功率曲线如图8 所示，仿真结果见表3。

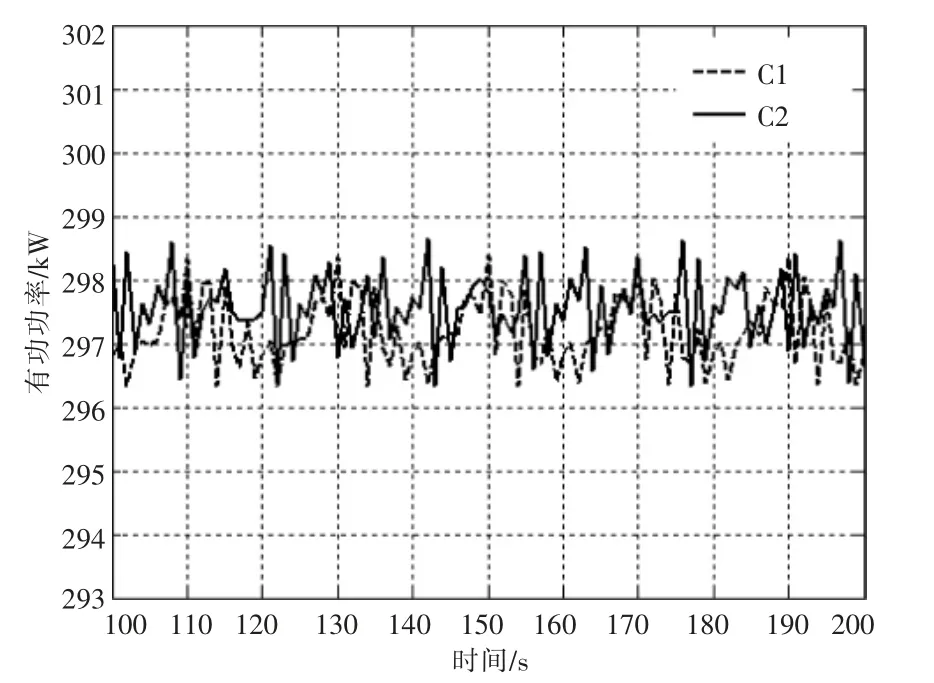
图8 风速6 m/s 空气密度修正前后的功率Fig.8 Electrical power before and after air density correction at wind speed 6 m/s

表3 恒定风况仿真实验结果Table 3 Result of simulation experiment in constant wind

根据图8 的仿真结果，空气密度修正前后，机组实际输出功率未得到明显提升。

由表3 可知，由于修正后的最优转矩控制系数变大，导致同等风速下风轮转速降低，计算得到叶尖速比相应地减小。根据图2 所示的叶尖速比和功率系数Cp的关系，可以计算得到相应的Cp值。修正后的功率系数与未修正的功率系数差别不大，仅提高了0.46%。与上述湍流风况下的仿真结果一致。因此，空气密度修正算法改变机组的风轮转速进而改变叶尖速比，但是由于Cp-λ 曲线顶部平滑，对Cp影响效果小。

5 结论

本文在分析空气密度对风电机组功率影响的基础上，结合风电场的实际环境数据，设计了基于空气密度修正的转矩控制算法。在不同的空气密度下进行仿真实验，并对实验结果进行总结分析，得到以下结论。

①风电场环境中，空气密度每天呈现周期性变化；并且，季节性变化为冬季大于夏季；整年呈近似正弦变化。空气密度受温度影响明显，在风电场没有气压传感器的条件下，可以采用实时温度进行近似估计。

②空气密度修正后的转矩控制算法对风电机组输出功率影响不明显。

③空气密度修正算法导致相同风速下的转矩、转速值显著改变，优化时须考虑对机组载荷的影响。

④空气密度的变化导致同一风速下机组的发电功率不同，在风电场功率曲线统计中应注意空气密度的修正。