“双球飞石索”的物理模型及影响其绕轴缠绕圈数的因素
陈逸嘉,何洪仁,邱孝兵,邓慧文,赵芸赫
“双球飞石索”的物理模型及影响其绕轴缠绕圈数的因素
陈逸嘉1,何洪仁1,邱孝兵1,邓慧文1,赵芸赫2
(1.四川省成都市温江中学,四川 成都 611130;2.首都师范大学附属中学,北京 100048)
为“双球飞石索”这一传统狩猎工具建立了一个简化的物理模型,对该模型中重物迅速静止的现象进行了理论分析与实验研究。从理论上分析了双球飞石索的动力学过程,并用Matlab软件数值求解了系统的运动轨迹,然后设计实验验证了理论模型的有效性。通过控制变量实验,探究了释放角度、轻重物质量之比、绳长、绳与杆的摩擦因数4个自变量对轻物端细线绕杆圈数的影响,得到的4个自变量对其影响的变化关系也与理论预测较为相符。
双球飞石索;运动轨迹;绕杆圈数;狩猎工具
双球飞石索是一种古代的经典狩猎工具,一根麻绳的两端点上缠绕固定两个石头就构成了其基本结构,如图1所示。古时候的狩猎者往往骑在飞驰的马匹上,瞄准猎物抛出飞石索,缠绕锁住猎物的脚或者脖子,其利用的原理正是自身结构的旋转缠绕特性。

图1 双球飞石索简图
本文在对飞石索狩猎这一工具的研究中,将其简化为竖直平面内的运动,其大致的运动过程为:将一根两端分别固定了轻重两物的长细绳挂在任意水平杆上,用手下拉轻物并吊起重物,释放轻物,它即会绕杆扫动,短暂时间后重物会突然停止下落,轻物及轻物端细绳继续绕杆旋转直至完全缠绕在水平杆上,便达到阻止重物落向地面的目的。该现象中由轻重两物及细绳组成的系统即为在竖直平面内运动的双球飞石索模型。本文对上述现象进行了理论分析并建立理论模型,将得到的动力学方程在Matlab中拟合,调整相关参数得出双球飞石索的轨迹动态图,将其与实验结果对比。通过实验探究了绕杆圈数与各变量之间的关系,这些结论在高空救援、逃生等方面有着重大意义,被救者常常会被当作重物,在紧急情况下,通过调节双球飞石索模型的相关参数来控制救援设备的初始条件,释放恰当的轻物,即可最有效、便捷地保证待救人员的人身安全。
1 双球飞石索的理论模型
1.1 双球飞石索现象的原理分析
根据《力学》(第三版)[1]可以得到双球飞石索现象中重物与轻物所受拉力的关系式:
1=2μα(1)
式(1)中:1为重物端绳上拉力,即重物重力;2为轻物端绳上拉力,且1>2;为自然底数;为绳与杆的静摩擦因数,而在绳与杆有相对运动时可将视为动摩擦因数;为绳与杆的包角。
在重物下落的过程中,轻物会绕杆扫动,包角逐渐增大,导致等式右侧指数倍增长,在某一极短时间内增加直至大于等于等式左边一项,绳上拉力大于等于重物重力,此时重物便突然停止。
1.2 运动全过程轻重物的动力学方程
在极坐标系下,将杆的横截面圆心看作极点,以竖直向上为极轴的正方向,极角取逆时针为正方向,如图2所示。
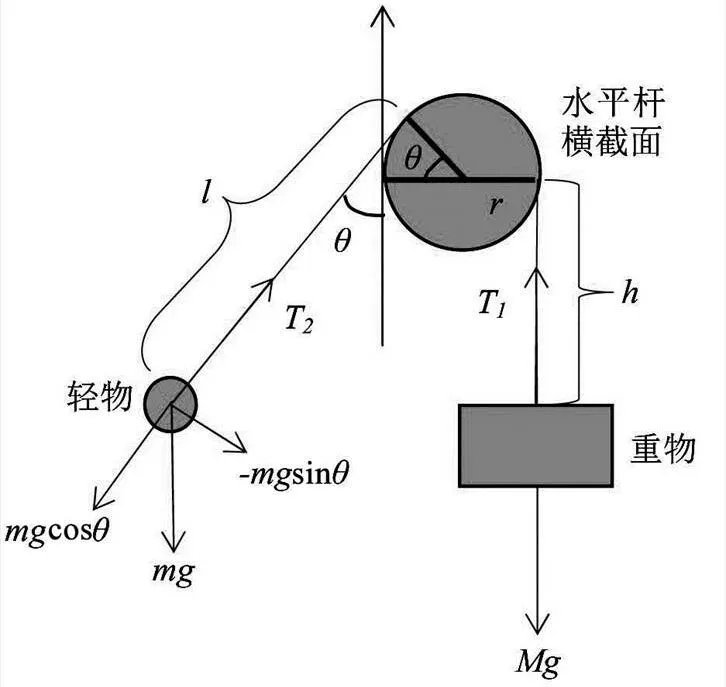
图2 双球飞石索运动过程中的受力分析示意图
分析轻物的运动,由几何关系可得:
=0--(π+) (2)
式(2)中:为轻物端绳长;0为绳总长;为重物端绳长;为杆的横截面半径;为轻物端细绳从=180°开始的绕转角度。
=π+(3)
对式(2)两边求导得:
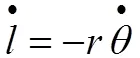
对轻物使用角动量定理,因为轻物绕绳与杆相交的切点扫动,而切点绕杆做圆周运动,所以以切点为旋转非惯性参考系,则有:
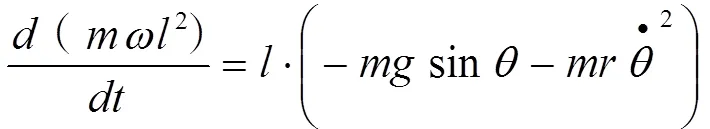
联立式(2)(4)(5)可得:
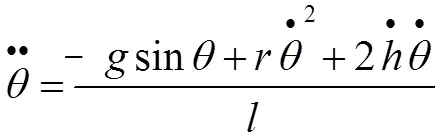
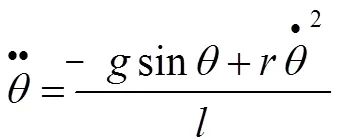
由重物的受力分析得:

对轻物进行径向受力分析得:
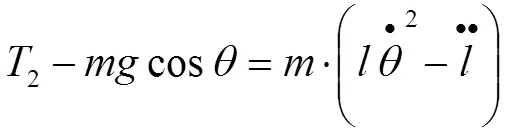
联立式(1)(3)(8)(9)得:

式(10)为重物运动全程的动力学方程,式(6)和式(10)这两个方程可分别描述双球飞石索轻、重物运动的轨迹,以及轻重物运动全程的速度、加速度、角速度、角加速度等运动学物理量随时间的变化特征。此外,也可基于这两式从不同目的对双球飞石索切入探究。将式(6)和式(10)代入Matlab进行数值求解即可模拟双球飞石索的运动。
在式(10)中,绳与杆的摩擦因数是不可忽略的,在Matlab中双球飞石索模型得以运行的前提是需要明确值。以下讨论测定的方法,并给出由本实验情况决定的值。
1.3 摩擦因数的测量
观察在包角为180°时,轻物竖直上升,重物竖直下落的情况。
设杆上细绳对杆竖直向下的压力为,如图3所示。

图3 绳对杆的压力示意图
正压力N则指向圆心,它与压力之间的关系为:

式(11)中:为正压力与竖直方向所成夹角。
通过微元法将绳对杆施加的正压力拆分成无数个绳微元对杆微元的正压力之和,从左到右为由90°减小为0°时,绳微元对杆微元的正压力变化趋势如图4所示。
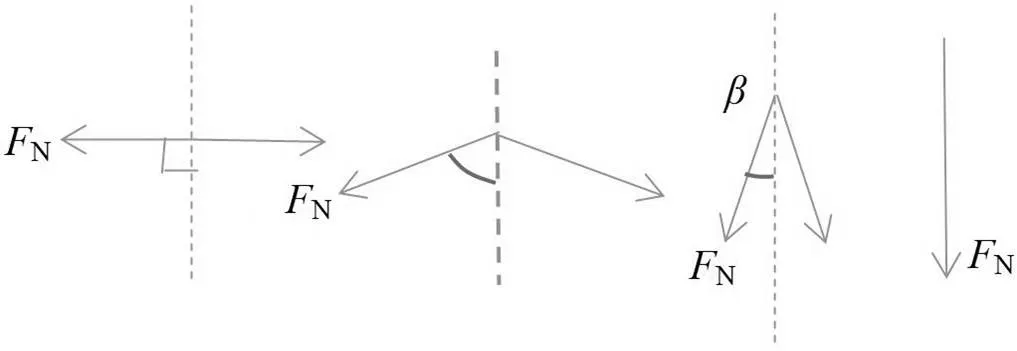
图4 绳对杆正压力变化示意图
从图4不难看出杆两侧正压力大小相同、方向恰好对称,由此可将对称的两侧正压力合成,得到:
N合=2Ncos(12)
联立式(11)(12)可得:
N合=2cos2(13)
对式(13)积分得:

在实验中,实际测量方案为:让轻重物两端细绳按图3所示方式竖直悬挂在水平杆上,用力的传感器在轻物端施加一个竖直向下的拉力,使系统处于静止状态。此时缓慢增大拉力,当重物匀速上升时,观察传感器显示屏上一段时间内保持不变的拉力值,并记录下来,用此值加上轻物重力后可得到轻物端细绳的拉力。
由受力分析可知,用轻物端细绳的拉力减去重物端细绳的拉力(即重物重力),得到滑动摩擦力,即:
=light-heavy(15)
式(15)中:light为轻物端细绳的拉力;heavy为重物端细绳的拉力。
此时,杆受绳的竖直压力为:
=light+heavy(16)
2 实验验证
2.1 实验装置及步骤
实验装置如图5所示,所用到的实验用品有铁杆、铁架台、金属垫圈、细绳以及自制量角器(用来控制初始的释放角度)。实验中,将杆用铁架台固定并保持其水平,再把两份数量不等的金属垫圈分别系在细绳两端,充当轻、重物。将细绳挂在杆上,下拉轻物使重物上升至一定高度,再使轻物端细线与相应的量角器刻度重合以达到控制释放角度的目的,然后释放轻物,用相机拍摄从轻物释放至轻重物完成运动后均静止的过程,并观察实验现象。将录制的视频导 入Tracker追踪轻物的轨迹得到实验数据,用其与理论结果比对。

图5 双球飞石索的装置实物图
2.2 实验验证
最直观的验证方法为对照轻物轨迹图,通过观察理论与实验得到的轨迹是否重合来判断理论是否合理。根据实验实际相关参数,设置Matlab求解双球飞石索运动程序中的初始变量值:选取水平杆横截面半径=0.012 m,绳与杆的摩擦因数=0.26,重力加速度=9.8 kg·m/s2,用轻重物质量之比(M/m)、绳总长0、初始释放角0等进行数值模拟预测,并与实验图像进行比对,=8、0=1.0m、0=90°条件下理论与实验的对比如图6所示。

图6 轻物轨迹的实验验证
对比多组理论和实验的数据之后,发现理论模拟与验证实验的轻物轨迹图基本重合,可以看出,理论与实验符合度较高。
3 影响绕杆圈数的因素
3.1 理论预测
绕杆圈数是描述双球飞石索现象的特征量之一。接下来讨论初始状态,即轻物释放前,绕杆圈数与绳长、释放角度、轻重物质量之比、绳与杆的摩擦因素等变量的关系。
直观感受是绕杆圈数与绳长正相关,但这样就忽略了轻重物质量之比的影响。实际运动并非那么简单,如果绳长过长,而轻重物质量又很接近,在这种情况下,极可能无法完成完整的运动:轻物还未绕过最高点,速度就减小为0,从而跌落返回。此时若绳长越短,绕杆圈数反而会越多,但这仅属于特殊情况。所以成正相关关系的条件为完成完整的双球飞石索运动。
由式(10)可知,在能完成完整的双球飞石索运动条件下,重物质量比轻物质量大得越多,重物竖直向下的加速度减小越慢,下落时间就会越长。可抽象地理解为重物端消耗的绳长更长,留给轻物端绕杆扫动的绳长自然更短,绕杆圈数也就更少。此时绕杆圈数与轻重物的质量之比的倒数正相关,但类比绳长的讨论,考虑这种情况:重物质量远大于轻物,而绳子恰巧较短,整个过程将会变得极为迅速,系统变得极不稳定,将很难确保它有较多的绕杆圈数。
绳与杆的摩擦因数也会存在影响。由式(10)不难发现,在能完成完整的双球飞石索运动的条件下,摩擦因数越大,重物竖直向下的加速度减小得越快,重物就会越早停止下落,于是重物端消耗的绳长更短,留给轻物端绕杆扫动的绳长会更长,绕杆圈数也就越多。
对于释放角度的影响,通过观察实验现象可知:释放角度过大或过小时,绕杆圈数往往都不会太大,而选取一个折中的范围绕杆圈数会更大,这很像二次函数的变化关系。
3.2 释放角度的影响
通过实验验证理论预测的结果,并在探究相关因素时使用控制变量法。在其他量不变时,释放角度范围选取30°~150°,中间取15°为间隔进行实验探究。在此基础上,讨论在不同释放角度下绕杆圈数的特点,重复实验,记录多组实验的圈数,取平均值作为实际圈数,绕杆圈数释放角度的函数关系如图7所示,以下对自变量的探究采用同样的方式。

图7 轻物绕杆圈数随释放角度变化的规律
轻物绕杆圈数随释放角度变化规律为:绕杆圈数与释放角度呈近似开口向下的二次函数关系变化,且最大值在释放角为90°~105°范围内,这也就意味着将轻物举起至水平面或略高于水平面时,其绕杆圈数达到上限,整个过程也就显得更稳定、更容易成功。但仍旧会发现此二次函数与轴交点并不是原点,当绕杆圈数为0时释放角度为一个稍大于0°的值,说明存在空气阻力等误差影响,结果比较符合现实中对双球飞石索物理过程的直观感受。
3.3 轻重物质量之比的影响
在其他量不变时,选取6~14为重物质量与轻物质量比的范围,中间取2个单位为间隔来进行实验探究,并给出了它的回归方程以及决定系数。绕杆圈数与轻重物质量之比关系如图8所示。

图8 轻物绕杆圈数随轻重物质量之比变化的规律
轻物绕杆圈数随轻重物质量之比变化规律:在能完成完整的双球飞石索运动的条件下,绕杆圈数与轻重物质量之比呈近似线性递减的关系变化。需要再次强调的是,此规律并不恒成立,正如3.1节所提到的,应加一个前提——能完成完整的双球飞石索运动。轻重物质量之比与绳长这两个自变量之间存在着某种内在联系,这种联系促使着它们不断影响着对方对应的应变量变化规律。在此将这条性质定义为自变量的非独立性;与之相反,如果单个自变量决定的应变量变化规律不受其他自变量的影响,则称之为自变量的独立性。从这个角度来看,轻重物质量之比、绳长、绳与杆的摩擦因数是非独立的,而释放角度、水平杆横截面半径、重力加速度则是独立的。
3.4 绳长的影响
在其他量不变时,选取0.6~1.4 m为绳长范围,中间取0.2 m为间隔来进行实验探究。绕杆圈数与绳长关系如图9所示。
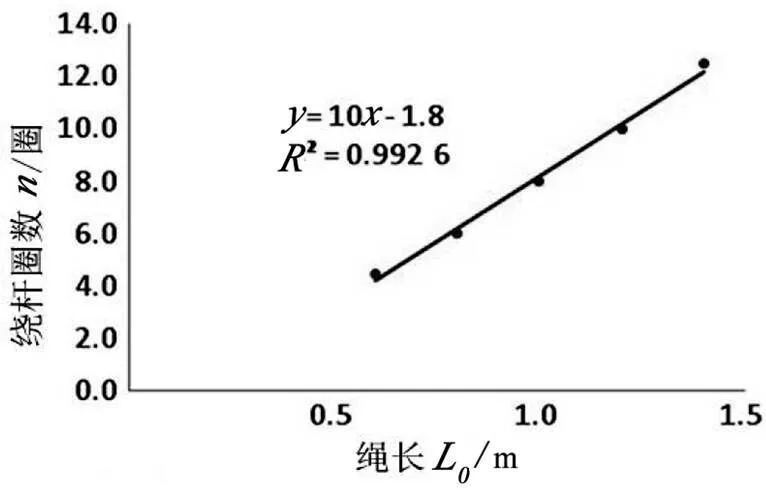
图9 轻物绕杆圈数随绳长变化的规律
轻物绕杆圈数随绳长变化规律为:在能完成完整的双球飞石索运动的条件下,绕杆圈数与绳长呈近似线性递增的关系变化。
3.5 绳与杆的摩擦因数的影响
在实验中不便于改变绳与杆之间的摩擦因数,因此,对于绕杆圈数随绳与杆的摩擦因数的变化规律可以通过理论模拟来观察。在其他量不变时,选取0.2~1.0为摩擦因数范围,中间取0.2个单位为间隔来进行实验探究。绕杆圈数与绳与杆的摩擦因数关系如图10所示。

图10 轻物绕杆圈数随绳与杆的摩擦因数变化的规律
轻物绕杆圈数随绳与杆的摩擦因数变化规律为:在能完成完整的双球飞石索运动的条件下,绕杆圈数与绳与杆的摩擦因数呈近似线性递增的关系变化。
回顾3.1小节的理论预测,将之后得到的实验规律与其相比较,从而也间接地验证了理论的正确性。
4 结论
本文建立了一种描述双球飞石索的运动过程的简单物理模型,并从理论和实验上对该模型进行了研究。
通过对比理论预测的轻物轨迹与实际轨迹验证了理论模型的有效性。除此之外,探究了绕杆圈数与如下4个自变量的变化关系:①与释放角度呈近似开口向下的二次函数的关系变化;②与轻重物质量之比呈近似线性递减的关系变化;③与绳长呈近似线性递增的关系变化;④与绳与杆的摩擦因数呈近似线性递增的关系变化。将理论结果与实验结果对比,发现两者轻物轨迹基本重合,且理论较为准确地预测了探究实验的结果,说明理论与实验较符。
[1]漆安慎,杜婵英.力学[M].北京:高等教育出版社,2012.
TP13
A
10.15913/j.cnki.kjycx.2020.02.001
2095-6835(2020)02-0001-04
陈逸嘉(2002—),男,四川成都人,四川省成都市温江中学高2018级学生。
赵芸赫(1993—),女,吉林长春人,物理教师,主要研究方向为物理课程与教学论、IYPT问题解决。
〔编辑:张思楠〕

