A constitutive model coupling damage and material anisotropy for wide stress triaxiality

Rui LI, Mei ZHAN,*, Zebang ZHENG, Hongrui ZHANG,Xiaolei CUI, Wei LV, Yudong LEI

a State Key Laboratory of Solidification Processing, School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China

b Shaanxi Key Laboratory of High-Performance Precision Forming Technology and Equipment, School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China

c Laboratory of Aero-engine High-Performance Manufacturing, School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an 710072, China

KEYWORDS Constitutive model;Damage evolution;Fracture criterion;Material anisotropy;Stress triaxiality

Abstract A constitutive model that can describe the damage evolution of anisotropic metal sheets during the complex forming processes which experience wide stress triaxiality history is essential to accurately predict the deformation and rupture behaviors of the processes.In this study,a modified Lemaitre damage criterion which couples with the anisotropic Barlat 89 yield function is established. The effects of stress triaxiality, Lode parameter and shear stress on damage accumulation are considered in the constitutive model.The model is numerically implemented and applied to fracture prediction in tensile tests with different stress triaxialities and a complex deformation process with wide stress triaxiality history. The good consistency of predictions and experiments indicates that the modified Lemaitre damage model has excellent fracture prediction ability. Finally, the accuracy of the model is analyzed and discussed.

1. Introduction

The rolling produced anisotropic metal sheets often experience a wide range of stress triaxiality history in complex plastic forming processes.1Due to the limited fracture strain and the high yield-strength ratio of these metal sheets, fracture may easily occur during the plastic forming processes. However,it is difficult to accurately predict the deformation behaviors and fracture of these metal sheets for their strongly anisotropic properties and the complex stress state varication history during the processes. Fortunately, numerical simulations provide a solution method. To establish a reliable model for numerical simulations can not only reduce the cost of repeated trial experiments, but also improve the production efficiency. The accurate prediction of the plastic deformation and fracture during the forming processes usually requires the secondary development of the constitutive model so that the model can be applied to specific forming processes. For example, it is necessary to implement the fracture criterion which considers a wide stress triaxiality history into the constitutive model to describe the shear spin forming process.

From microscopic viewpoint, the fracture behaviors of metal sheets consist of nucleation, growth and coalescence of microscopic voids.2-4The fracture criteria can be categorized into coupled and uncoupled criteria for whether the cumulative damage induced softening mechanism is considered.Uncoupled fracture criteria,5-10which don’t consider the softening behavior generally have a simple form. They are relatively easy to be numerically implemented and with fast calculation speed. However, the softening caused by damage is a crucial mechanism for some materials and cannot be ignored.While coupled fracture criteria,consider the softening mechanism. Depending on what length scale the criteria is based on, coupled fracture criteria can be further categorized into the Gurson series11-13and the Lemaitre series.14

The Gurson series fracture criteria were developed at microscopic level where the damage accumulation is quantified by void volume fraction. The Lemaitre series fracture criteria were introduced based on macroscopic continuum damage mechanic (CDM). One common drawback of the both series is that they did not consider the contribution of shear stress to fracture and hence they are inaccurate of fracture prediction in low stress triaxiality15-19. To overcome the drawback, the Gurson-Tvergaard-Needleman (GTN) model was proposed15,16,20by incorporating the damage growth under low stress triaxiality for shear-dominated stress state. However,as pointed out by Khan and Liu21, there are more than ten parameters that need to be identified in these recently developed GTN models. Some of these parameters are coupled to each other and even complex stochastic methods need to be used in order to determine all of them. Compared to the GTN series,the parameter determination in the Lemaitre damage model is much easier, which only requires a few macroscopic mechanical tests. Therefore, the Lemaitre damage model is widely used in the prediction of damage evolution and ductile fracture.22-24Similar to the GTN damage model,the Lemaitre damage model also has the defect of inaccurate predicting damage localization under shear stress state with low stress triaxiality.18,19The reason is that the stress triaxiality in the Lemaitre model only reflects the values of the hydrostatic stress components, while not takes the third deviatoric stress invariant (or Lode parameter) into account. In 2004,Bao and Wierzbicki25found that stress triaxiality alone was not sufficient to the characterization of ductile fracture. A large number of studies26-28have shown that the Lode parameter is also a crucial factor in predicting fracture. In addition,the second defect of the Lemaitre damage model is that the square form of the stress triaxiality cannot explain the differences in damage evolution between the positive and negative stress triaxialities. Furthermore, the above damage models didn’t consider the material anisotropy, while more and more scholars have gradually realized that material anisotropy has an important effect on damage accumulation. Park et al.29studied the anisotropic fracture behavior of the DP980 sheet by modifying the DF2014 fracture model. Lou and Yoon4put forward an anisotropic fracture model to normalize the fracture strain of AA6K21 in different directions from the RD through a linear transformation. Lately, in 2019, Lou and Yoon30proposed an anisotropic ductile fracture model by introducing the anisotropic Hill 48 yield function into the weight function of the DF2016 model for fracture prediction of the AA6082-T6. Zhang et al.31proposed an anisotropic thermo elasto-viscoplastic fracture model with a distortion strengthened yield surface. Kassar et al.32established a timedependent damage-coupled anisotropic plasticity model to capture the strain-rate effect at variable temperatures for Mg AZ31B alloy.

Meanwhile, many scholars have modified the Lemaitre damage model to apply it to anisotropic material, negative or low stress triaxiality stress states, thereby achieving better fracture prediction in various plastic forming processes. For example, Li et al.33replaced the Mises equivalent stress in the original Lemaitre damage model with an anisotropic Hill 48 one to describe the damage evolution in anisotropic plastic material.Ghorbel et al.34,35investigated the anisotropic elastoplastic model coupled with CDM damage model for fracture prediction of DD13 metal sheet.Tang et al.36proposed a modified Lemaitre damage model to predict the fracture of 22MnB5 high strength steel sheets by taking the influence of temperature and strain rate into account. To overcome the under-estimation of the damage value under low stress triaxiality, Cao et al.18,19implemented the Lode angle parameter into the Lemaitre damage dissipative potential to consider the effect of shear stress to damage accumulation. Besides, in order to describe the damage accumulation differences between the positive and negative stress triaxialities,Bouchard et al.23believed that the accumulation of damage in the Lemaitre damage model occurred only in the tensile stress state. However, a large number of literatures3,25-27have indicated that the damage still occurs in the stress triaxiality range from-1/3 to 0.Similarity,Lemaitre and Desmorat37and Cao et al.18,19introduced a material constant h to explain the crack closure effect under compressive stress state,i.e.negative stress triaxiality. However, there are some contradictions exit in these modified Lemaitre damage models, which make them inapplicable for complex deformation processes. Firstly, the micro-crack in material is considered to be partially closed only under the compressed state, while the damage accumulation velocity is identical under tensile and compressive stress states.Secondly,the damage value should decrease under compressive stress state for the effective bearing area increases with micro-crack closing.In addition,the above modified Lemaitre damage models are mainly used in proportional loading processes with a narrow range of stress triaxiality fluctuation and lacking fracture models coupled with plastic anisotropy for complex deformation that metal sheets may experience a wide stress triaxiality fluctuation history.

In this study, a constitutive model for damage evolution and fracture prediction of anisotropic metal sheets for complex loading conditions is developed. The Lemaitre damage model is modified and used to predict fracture with a wide stress triaxiality variation range (about -1/3-2/3). The Barlat 89 yield criterion38is used to describe the anisotropic plastic deformation behavior of the metal sheets. The paper is structured as follows. In Section 2, a constitutive model, which depicts a modification of Lemaitre damage model coupled into the Barlat 89 yield criterion is introduced. Section 3 describes the parameter determination processes of the constitutive model.In Section 4,we describe the experiments and the corresponding finite element (FE) models which are used to validate the established constitutive model. The main results of the experiments and simulations are presented and discussed in Section 5.Finally,we conclude with the key findings in the present study.

2. Modification of constitutive model

Constitutive characteristic is a crucial issue to investigate the plastic deformation behavior of metallic material.39In order to take the anisotropic properties of metal sheets and damage into account under complex stress states during plastic forming processes, a modification of Lemaitre damage model coupled into the Barlat 89 yield criterion (forming the MLB constitutive model) is introduced in this section.

2.1. Lemaitre damage model

The original Lemaitre damage criterion is based on the assumption of continuum thermodynamics and strain equivalence.With the assumption of strain equivalence,the deformation behavior of the damaged materials can only be reflected by the effective stress.14Thus, the constitutive model of the damaged materials can take the non-destructive form just by replacing the ideal stress with the effective stress as Eq. (1).

where, ^σ is the effective stress, σ the ideal stress and D is the isotropic damage.In the constitutive model,the effective stress^σ is adopted instead of the ideal stress σ to describe the effect of damage on materials’ mechanical properties. In the Lemaitre damage model, the internal state variables include elastic strain εe,equivalent plastic strain¯εp,damage D and hardening parameter rk. Based on these state variables, the thermodynamic state potential is defined as φ=φe+φp. Here, φeand φpare Helmholtz free energy and plastic potential,respectively and are expressed as Eq. (2).

where, ρ is the material density, Cijklthe elastic matrix andis the isotropic hardening force conjugate to r. State forces are determined by the state potential and are defined as Eq. (3).

where, Y is the damage energy release rate, E the Young’s modulus, σ-the equivalent stress, ν the Poisson ratio and σmis the mean stress. The material damage highly depends on the energy dissipation potential in the plastic deformation processes. The energy dissipation potential is decomposed into plastic and damage parts as Eq. (4).

in which, εDis the plastic strain at which damage value begins to accumulate,εRthe fracture strain with a constant value,Dcthe damage threshold at fracture moment and n is the hardening exponent.

2.2. A modification of the Lemaitre damage criterion

In order to achieve the fracture prediction in a wide stress triaxiality range for anisotropic metal sheets, a modified Lemaitre damage criterion is proposed in this study. The modification consists of three aspects: (1) the damage dissipative potential from Cao’s modification18,19is adopted in the Lemaitre model to consider the shear stress to damage accumulation; (2) a stress state related fracture strain is adopted to distinguish the different damage cumulative rates under differing stress states; and (3) the von Mises stress in the Lemaitre-based criterion is approximately replaced by an anisotropic plasticity related effective stress to incorporate the effect of plastic anisotropy on damage cumulations. The numerical implementations of the modification are described as follows:

Firstly, the modified damage dissipative potential from Cao’s18,19is as Eq. (9).

Secondly, one assumption has been made in the original Lemaitre damage criterion is that the fracture strain is a constant. However, a lot of studies26-28have demonstrated that the fracture strain¯εf(to distinguish the constant fracture strain εRin original Lemaitre damage model) is a function of stress triaxiality η and Lode parameter L as in Eqs. (11-13). It is worth noting that the Lode parameter L in Eq.(13)is different from the Lode angle parameterin Eq. (9), while there is a relation40between them as Eq. (14).

Thirdly,in order to incorporate the effect of material anisotropy into the model, von Mises stress in Eq. (10) is approximately replaced by an anisotropic plasticity related equivalent stress σ-.It also has been demonstrated that the anisotropic plasticity can be coupled with the Lemaitre-based damage model to assess the damage evolutions.33Meanwhile,a cut-off value of-1/3 for stress triaxiality is adopted for simplicity and fracture does not occur if the stress triaxiality falls below that value.25Therefore,the modification of the Lemaitre damage criterion is written as Eq. (15).

2.3. MLB constitutive model

A constitutive model usually consists of three components:i.e.yield criterion, flow rule and hardening criterion as Eq. (16).

in which, f is the yield function and σsis the flow stress.

Considering the damage softening effect, the MLB model thus can be constructed by incorporating the yield criterion with the above modified Lemaitre criterion as Eq. (17).

The flow stress σsin Eq. (17) is described by a Hollomon hardening model as Eq. (22).In this study,a constitutive model with small-strain hypothesis and the semi-implicit return-mapping algorithm41are adopted for the model numerical implementation.The detailed implementation process is shown in Appendix A.Based on the small-strain hypothesis, calculations with the MLB model are a bit at the cost of solution accuracy compared with some finite strain-based models31-35,while numbers of solved equations in the MLB model are less and with easy convergency and high computational efficiency.42In addition, due to the semiimplicit return-mapping algorithm, convergent results can be easily achieved compared with the implicit algorithm.43With above two features,the MLB model may have a wide application potential for fracture prediction in some complex plastic forming processes. However, in the semi-implicit returnmapping algorithm, the plastic flow direction rnis determined by σnat the beginning of the iteration step(Fig.A1).With this special return-mapping algorithm, if the difference between σnandis very large, it is possible that the adjusted stress cannot return to the newer yield surface. In other words, the adjusted stress cannot return to the new yield surface under a large time step, which leads to the failure of the algorithm.To avoid this failure, the maximum time increment is needed to be carefully limited in a reasonable range for some complex loading cases.

3. Parameters determination

Constitutive model fully coupled with damage(MLB model)is characterized with three groups of material parameters as follows:

- Five parameters to capture the anisotropic yield behavior,including a, c, h, p, m;

- Two parameters to describe the hardening behavior,including K, n;

- Nine parameters to define the damage evolution in the modified Lemaitre damage model, including Dc, εD, α1,α2, C0, C1, C2, C3, C4.

The above three groups parameters will be determined in the following sub sections.

3.1. Parameters to capture anisotropic yield behavior

Uniaxial tensile tests along 0°, 45° and 90° from the rolling direction (RD) of the 2219-O aluminum alloy sheet with 2 mm thickness were carried out using an Instron 3382 electronic universal testing machine and the stress-strain responses were recorded, as shown in Fig. 1. The influence of material anisotropy on stress is weak at the onset of deformation stage and becomes significant with the increasing of the strain. The maximum difference of the stress value between 0° and 45°specimens is about 12 MPa.

Fig. 1 Stress-strain responses of 2219-O along different directions from the RD.

In dog-bone tensile test, combining with the DIC testing system(Fig.2),the Lankford coefficients can be obtained with plastic strains in the direction of stretching and width.A layer of white paint was sprayed on the surface of the specimen to form the white background, then the small black paint particles were sprayed on the top of the background. Two highspeed cameras were used to collect the speckle image of each deformation stage of the target deformation area and to calculate the full field strain and deformation. Finally, the anisotropy coefficients of the specimens in the 0°, 45° and 90°directions from RD were obtained as: r0=0.492,r45=0.787, r90=0.462.

Then, a=1.3544, c=0.6456, h=1.0215 in the Barlat 89 were identified according to Eq. (19). According to Eq. (20)and with φ=45°,a Newton iteration method is used to obtain the parameter p=1.115 and the squared residual SSE is equal to 1.093×10-9.

3.2. Parameters to describe the hardening behavior

With the isotropic exponent hardening model,the least square method is used to fit the plastic part of the experimental stressstrain curve (0° orientation). Then the isotropic hardening parameters K and n were obtained as 259.1 MPa and 0.218,respectively, with a high fit quality (R2) of 0.994.

3.3. Parameters in the modified Lemaitre damage model

To obtain fracture strains of the 2219-O aluminum alloy sheet under different stress triaxialities, specimens with five type shapes were designed (Fig. 3) and an integrated experimental and numerical calibration method was adopted.The five types of specimens in the figure were firstly stretched to obtain the experimental load-displacement curves and then their corresponding FE models were established for curves calibration.

Fig. 2 Strain fields calculated with a DIC testing system.

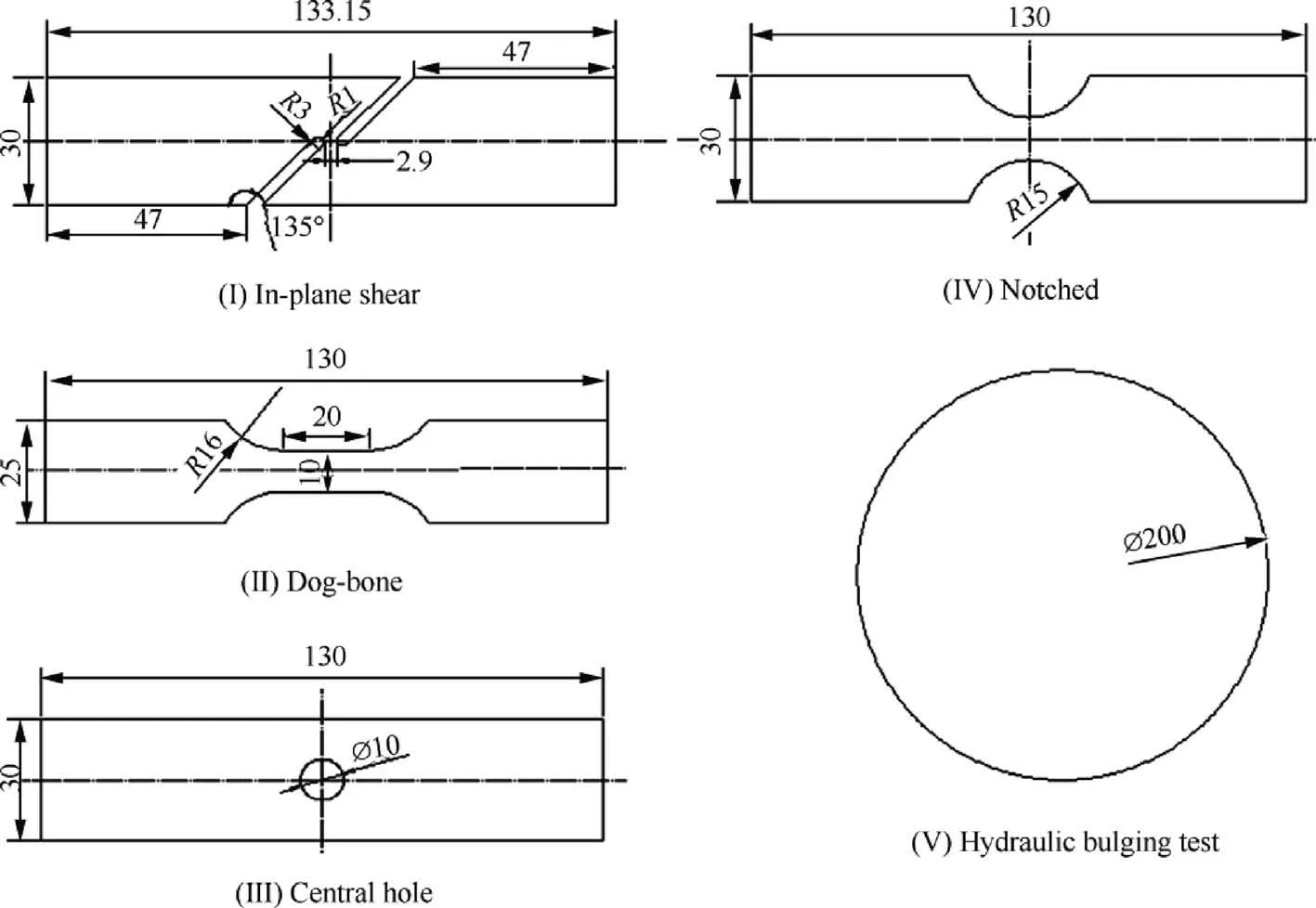
Fig. 3 Five types of specimens (unit: mm).

Fig. 4 Elongations and bulging height after fracture.

Since the experimental fracture is notoriously subject to statistical spread,six repeated tests of each loading type were carried out and the elongations (bulging height for type V) after fracture were summarized in Fig.4.In the figure,the 95%confidence intervals were also added to show the statistic distributions. Then, the specimen with the elongation which is the closest to the average value was chosen for the calibration of FE model and the determination of the facture strain. The maximum equivalent plastic strains obtained from the simulations at the experimental fracture moment(Fig.5)were viewed as the fracture strains. It should be noted that during the each one loading deformation processes with specimens in Fig. 3, their stress triaxialities will change slightly. Therefore,Eq. (28) was used to represent the average value of stress triaxiality in one deformation process, as ref.44. Besides, the central region of the shear specimen is close to the pure shear stress state, and the equivalent plastic strain that extracted from the central region is the concerned value at the fracture moment. The determined fracture strains under different

stress triaxialities are listed in Table 1.

Parameters Dcand εDin the modified Lemaitre damage model are equal to the original Lemaitre damage model’s.Their values were calibrated by achieving the minimum difference of simulated load displacement curves with the experimental ones in dog-bone tensile test. Finally, parameters Dcand εDcan be inversely obtained as 0.22 and 0.01, separately.With the same method in shear test, the shear stress related parameters of α1and α2in the MLB model can also be inversely obtained as 0.24 and 0.76, separately.

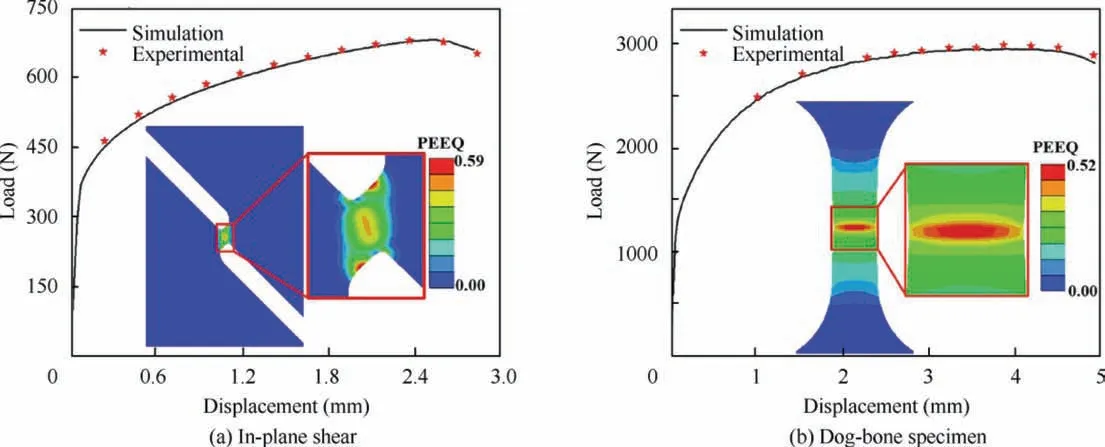
Fig. 5 FE simulations to obtain fracture strains.

Table 1 Fracture strains of 2219-O under different stress triaxialities.

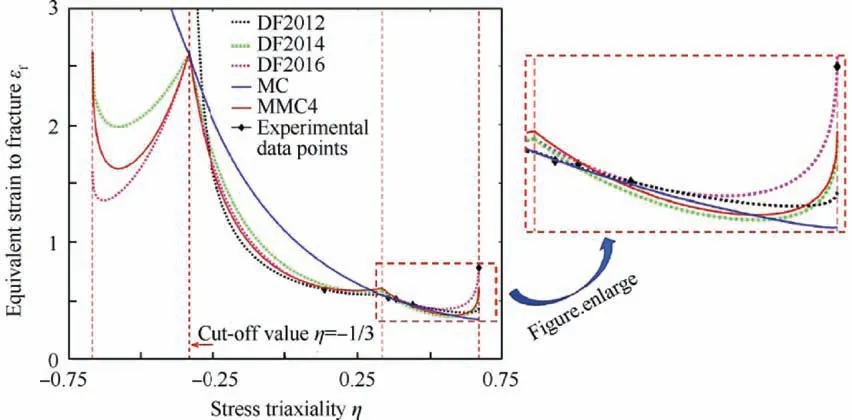
Fig. 6 Fitting of experimental data by different fracture models in space of

Fig. 7 Specimens with positive stress triaxiality ((Ⅰ) shear; (Ⅱ)dog-bone; (III) hole; (Ⅳ) notched; (V) hydraulic bulging test).

4. Application of the MLB model

Based on the VUMAT interface in ABAQUS software, the MLB model is implemented to FE simulation via the Fortran code,thereby achieving its applications in various plastic forming processes. To evaluate fracture prediction ability of the MLB model in both positive and negative stress triaxialities,specimens with different positive stress triaxialities in tensile tests were firstly designed the same as Fig.3.Since compressive fracture strain of the 2219-O aluminum alloy thin sheet by the uniaxial compression test is difficult to obtain.Shear spinning,which associates a significantly compression stress state was used for the model evaluation in negative stress triaxiality.Experiments of tensile tests with different stress triaxialities and a shear spinning process were carried out first and then the FE models of these experiments were established and conducted to evaluate the performance of the MLB model.

4.1. Experiments

Five types of specimens with different stress triaxialities in their loading processes in Fig.7 were used to verify the performance of the MLB model under positive stress triaxiality.The sizes of the specimens are shown in Fig.3.The first four types of specimens were cut along their rolling direction RD. These five types of specimens cover various of stress states from pure shear(near zero stress triaxiality)to hydraulic bulging test(2/3 stress triaxiality).All the specimens were loaded until fracture.The tensile rate was controlled as in Ref. [26], so that the central strain rate is about 10-3mm/s. The hydraulic bulging test was used to measure the fracture strain in the balanced biaxial tension state with 200 mm diameter of the circular blank.

In addition,shear spinning was used to evaluate the performance of the MLB model under negative stress triaxiality.During the shear spinning, the motor drives the mandrel to revolve around the central axis. Pressure is applied by the tail to ensure the blank to rotate synchronously with the mandrel.Meanwhile, the roller is fed along the profile of outer surface of the mandrel. With rotation of the mandrel and feed movement of rollers, the blank is tightly adhered to the mandrel to form a component with the similar shape as outer surface of the mandrel, as illustrated in Fig. 8(a). The used blank is the 2219 aluminum alloy sheet with a diameter of 780 mm as in Fig.8(b).The experiments were conducted on a CZ900/2CNC shear spin machine with SINUMERIK 840D operating system and the blank surface was lubricated with MoS2to reduce friction.

4.2. FE models

FE models were established with the ABAQUS software to simulate the experiments in Section 4.1.In the simulation processes of shear test,dog-bone tensile test,a central hole tensile test and notched tensile test, completely fixed constraints were adopted at one end of the specimens and the clamping parts by the chuck were constrained as rigid bodies to keep the conditions in the simulation completely consistent with the experiment. In the simulation of hydraulic bulging test, negligible deformation occurs in the blank holder and the concave die,so they were all set as discrete rigid bodies for computational efficiency.

Mesh sensitivity analysis of the FE models corresponding to the loading processes with specimens were performed based on the equivalent plastic strain and damage value of a typical element at the experimental fracture moment.Taking the dogbone tensile test and hydraulic bulging test as examples in Fig. 9, the figure shows that with the decreasing element size,the equivalent plastic strain and damage values in dog-bone tensile test gradually converge as the element size is less than 0.25 mm. Meanwhile, in hydraulic bulging test, the numerical results gradually converge when the number of element along the circumferential direction exceeds 150. Similarly, the minimum mesh sizes of the pure shear, hole and notched FE models were determined as 0.2 mm,0.25 and 0.25 mm,respectively.

In the FE model of shear spinning (Fig. 10(a)), the blank was fixed with the mandrel to ensure the blank and mandrel rotate synchronously. A discrete rigid body was used for the mandrel,analytical rigid bodies for two rollers and deformable shell element for the blank for computational efficiency.Surface-to-surface contacts were used between the roller and blank, also between the mandrel and blank. The coefficients of friction between the blank and rollers, between the blank and surfaces of mandrel were set as 0.02 and 0.2,46respectively.The mesh strategy of the blank is shown in Fig. 10(b). Fournode shell elements with reduced integration (S4R) were mainly used to discretize the blank and triangular S3 shell elements were used as transition elements in the radial direction to control the element size. Theoretically, it is more appropriate to use 3D solid elements in shear spinning, while considering the time-consuming with 3D solid elements, the 2D shell elements were still adopted in this study. In addition, a hourglass control scheme was adopted to avoid excessive element distortions. Detailed shear spinning parameters for the FE model are summarized in Table 2.

Since the semi-implicit return-mapping algorithm is adopted, the computational cost in complex loading cases is severely dependent on the quality and quantity of the mesh elements and it may quickly become prohibitive if even a single mesh element is very small,especially for a progressive forming process such as shear spinning where large plastic deformations occur locally, it is important to choose an appropriate element size to balance the computational accuracy and efficiency. Hence, the element size of the spun blank is chosen to be as uniform as possible with no bad quality warning elements and it is necessary to avoid small elements when generating the mesh.In order to find the appropriate element size,a mesh sensitive study was carried out using six sets of element sizes as shown in Table 3. The damage value D at the experimental fracture moment was extracted from each model and the computational cost was recorded as shown in Fig. 11.The figure shows that the simulation time increases dramatically with the total number of elements,but the predicted damage value only increases slightly when the element number exceeds 14000. Furthermore, the predicted fracture location varies in Models 1-3 but is identical in Models 4-6. Hence,Model 4 with the total number of elements 14,612 was used for the subsequent analysis. The average element size of the blank in the present model is 6 mm while the minimum size is 2.5 mm. Using this mesh strategy, the calculation time for the shear spinning is about 367 h, which is still long but acceptable.

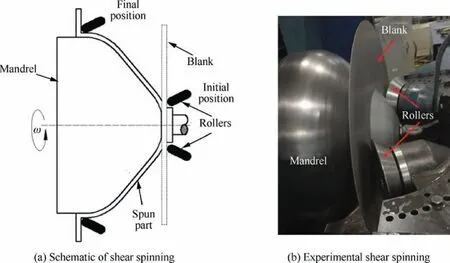
Fig. 8 Shear spinning process.

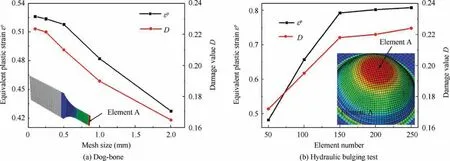
Fig. 9 Sensitivity analysis of element sizes.

Fig. 10 FE model for shear spinning.

Table 2 Fundamental parameters of 3D FE analysis for shear spinning.

Table 3 FE models with different mesh sizes.

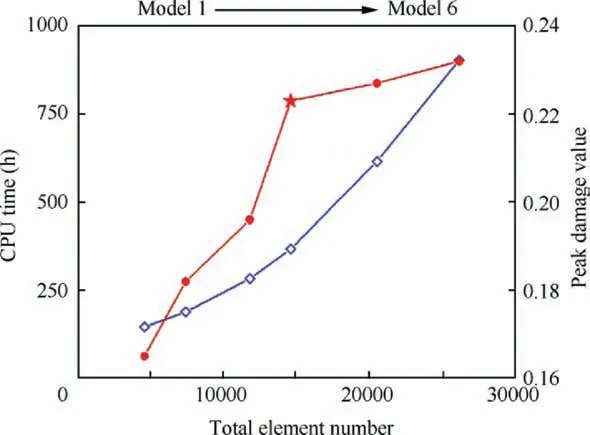
Fig. 11 Mesh sensitivity analysis in shear spinning.

During the shear spinning, the deformed area is subjected to squeeze followed by pulling of the rollers and the stress state of the material changes from compressive to tensile stress state as in Fig. 12. There is obvious negative stress triaxiality in shear spinning deformation, which is suitable for evaluating the performance of the MLB model under negative stress triaxiality.

5. Results and discussion

Fig. 12 Stress triaxiality distribution in deformation zones.

The evaluation of fracture prediction ability of the MLB model requires the assessment of the performance both under positive and negative stress triaxialities. Under positive stress triaxiality, the MLB model is directly compared with the tensile tests. Under negative stress triaxiality, the MLB model is indirectly compared with the shear spinning experiment. The performance of the MLB model under both positive and negative stress triaxialities is analyzed in this section together with the discussion of the reasons for fracture prediction accuracy of the model.

5.1. Performance of the MLB model under positive stress triaxiality

The evaluations of the MLB model under positive stress triaxiality were accomplished by comparing the experimental loaddisplacement curves. Fig. 13 shows the results of in-plane shear,uniaxial tensile test,hydraulic bulging test and their distribution of damage value D at the experimental fracture moment.There are good agreements of the load-displacement curves for all three types of the experiments. The damage values all reached the critical value of 0.22 at fracture moment.Hence,the MLB model can well predict fracture in tensile tests with different stress triaxialities of about 0, 1/3 and 2/3. The fracture in shear test occurs along about 45° of the loading direction and the fracture surface is flush with no obvious torsion phenomenon.The fracture occurs in the middle gauge section of the uniaxial tension specimen and there is no obvious necking phenomenon, which is consistent with the fracture characteristics of the typical light alloy sheet.

Meanwhile,the strain distributions were compared between simulations and the DIC measurements for a specimen with a central hole and a notched specimen as in Fig.14(a)and 14(b)respectively. The results demonstrate that the MLB is able to predict the macroscopic load-displacement responses as well as the local strain distributions. By integrating Figs. 13 and 14, it can be concluded that the MLB model can well predict the fracture of the 2219-O aluminum alloy specimens under positive stress triaxiality.

5.2. Performance of the MLB model under negative stress triaxiality

Fig. 14 Load-displacement responses and strain distributions at fracture moment between experiments and simulations.

To evaluate the fracture prediction ability of the MLB model under negative stress triaxiality, the FE model of the shear spinning was established and compared with the experiment.Fig. 15 shows the experimental fracture in shear spinning and the corresponding distribution of damage D predicted by the MLB and the original Lemaitre damage models, separately. It can be seen that the maximum damage reached the critical value with the MLB model when the experimental rupture occurs,while the maximum damage is about 0.28 with the original Lemaitre model.Hence,the original Lemaitre damage model predicts the larger damage value,while the MLB model can well predict the fracture under negative stress triaxiality as in shear spinning.

Fig.16 is the rupture progress predicted by the MLB model during the shear spinning.At 431.21 s,the cumulative damage reaches the critical value and the crack at the end of the spinning part begins to emerge (point A). With the spinning process going on, the rupture cavity gradually grows. At 433.25 s, a long and thin crack formed along the circumferential direction at the end of the spinning part and caused fracture of the spun component finally.

Fig. 17 shows the evolutions of the damage value D, stress triaxiality η,Lode parameter L and fracture strain¯εfof one element near to the crack initiation point A as in Fig. 16. The damage value increases with the spinning process going on.The stress state during the spinning process changes significantly, which results in a wide fluctuations of the stress triaxiality. This phenomenon is remarkably different from simple tensile tests as refs.26,45. The fracture strain and the Lode parameter also fluctuate with the stress triaxiality. In general,fracture strain fluctuates oppositely with the stress triaxiality for the fracture strain increasing with the decreasing of stress triaxiality.

5.3. Analysis of the fracture prediction accuracy

Fig. 15 Experimental and FE predicted fracture in shear spinning.

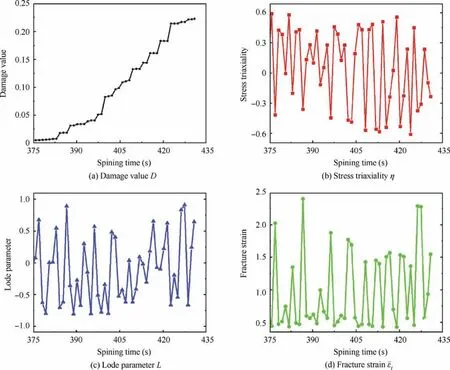
Fig. 17 Damage, stress triaxiality, Lode parameter and fracture strain variations in shear spinning.

In order to investigate reasons for fracture prediction accuracy with the MLB model in shear spinning, comparisons of the accumulated damage values in the same fracture area of the MLB model, the modified Lemaitre damage model coupled to the von Mises yield criterion (MLM model), the MLB model with a constant fracture strain (MLBC) obtained from the dog-bone tension and the MLB model without considering the shear stress to damage accumulation(MLBNS model as in Eq. (30)) at the experimental fracture moment in shear spinning were plotted in Fig. 18. As seen, ignoring the anisotropy of the material will make the predicted damage value nearly 25%higher than its threshold. With a constant fracture strain in the MLB model, the predicted damage is significantly greater than its threshold and even exceeding its threshold about 57%. Without considering the effect of shear stress,the accumulated damage is only 0.157 in the MLBNS model and is far below its threshold at the fracture moment.

The effect of shear stress is not incorporated in the MLBNS model, hence the predicted damage value at the experimental fracture moment in shear spinning is lower than the MLB’s. Shear stress contributes to the damage accumulation and accelerates fracture during plastic deformation process can also be found in refs.3,18,19. In order to further study the effect of shear stress on damage accumulation, one element near to the fracture area was selected to analyze its equivalent stress, shear stress and damage evolution history during the shear spinning process as shown in Fig. 19. It can be seen that there exists significant shear stress in the shear spin forming process as in Fig. 19(a).The accumulated damage using the MLB model and the MLBNS model are compared in Fig. 19(b). Without considering the effect of shear stress, the predicted damage is significantly reduced and the shear damage contributed about 29.6% of the total accumulated damage at the experimental fracture moment. Hence, it is necessary to incorporate the shear stress effect in the fracture model in shear spin forming process.

Fig. 18 Comparison of damage values in shear spinning using different damage models.

In order to further study the effect of material anisotropy on plastic deformation in shear spinning,the same ID number of elements near to the fracture area in the MLM and MLB models were selected separately to analyze their equivalent stress, equivalent plastic strain and damage evolution history as in Fig.20.From Fig.20(a),it can be known that the evolution history of equivalent stress in the MLB and MLM models both have wide range of fluctuations.The curves of equivalent stress in the MLB and MLM models intersect to each other,while the equivalent stress predicted by the MLM model is greater than that predicted by the MLB at the most time during the shear spin forming process. From Fig. 20(b), it can be known that both the equivalent plastic strain PEEQ and damage D in the MLM model are larger than those in the MLB.The damage D in the MLM model is about 25% higher than its threshold of 0.22. The reason is that the yield locus of the Barlat 89 criterion is inside in the Mises,which results in a larger predicted equivalent stress in the MLM model than the MLB and further lead to the greater equivalent plastic strain PEEQ and damage D.

Fig. 19 Stress evolution and comparison of accumulated damage with MLB and MLBNS models in shear spinning.

Fig. 20 Comparison of MLM and MLB models.

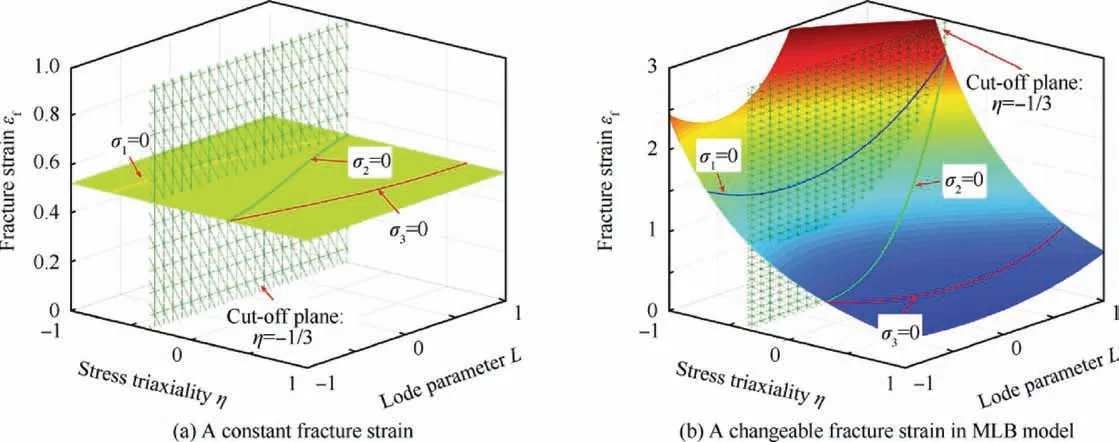
Fig. 21 Fracture locus of the 2219-O sheet in space of （η ，L，¯εp）.

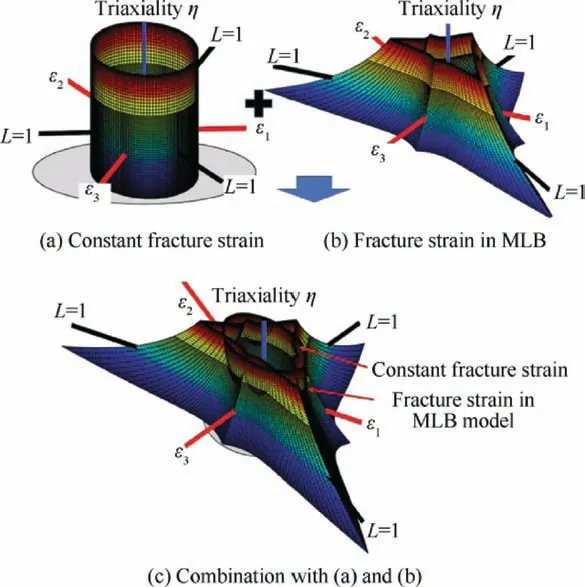
Fig.22 Fracture locus of the 2219-O in the principal strain space of (ε1, ε2, ε3).

6. Conclusions

In this study, a modified Lemaitre-based constitutive model is established by incorporating with the Barlat 89 anisotropic yield criterion. The model is applied to fracture prediction in tensile tests under different positive stress triaxialities and a shear spinning process with wide stress triaxiality history.The main findings are as follows:

(1) The Lemaitre damage model was modified by re-defining the fracture strain as a function of stress triaxiality and Lode parameter, meanwhile considering the effects of shear stress to damage accumulation.Then the modified Lemaitre damage model was coupled into the anisotropic Barlat 89 yield criterion to form an MLB constitutive model.Finally,the model was numerically implemented by the semi-implicit return-mapping algorithm.

(2) The good consistency of simulations and experiments in the fracture prediction of tensile tests and shear spinning process indicates that the MLB model is able to predict fracture in both positive and negative stress triaxialities.

(3) Applications of the model in shear spinning indicate that the contributions caused by shear stress accounts for 29.6% of the total cumulative damage. Ignoring the effect of material anisotropy and the variation of fracture strain will make the accumulative damage higher than their threshold value by about 25% and 57%,respectively. The MLB model takes both effects into account, which makes it with much accurate fracture prediction ability for the plastic forming processes with wide stress triaxiality ranges.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgement

This study was co-supported by the National Science Fund for Distinguished Young Scholars of China (No. 51625505), the National Natural Science Foundation of China (Nos.U1910213 and U1937203)and the Independent Research Project of State Key Laboratory of Solidification Processing of Northwestern Polytechnical University (No. 2019-TZ-02).

Appendix A. . Numerical implementation of the MLB constitutive model

From Eq. (A6), the state variablescan be obtained.

Thirdly,since the direction of plastic flow and the changing rate of the internal variable are determined at the beginning of each time step, their gradientsanddo not appear anymore in Eq.(A6).In addition,the plastic strain and the update of the internal variables are linear related to Δλ.Therefore, the first two terms of Eq. (A6) can be abbreviated as Eq. (A7).

Fig. A1 Semi-implicit return-mapping algorithm for stress update.

Meanwhile, with the assumption of incompressible volume in plastic deformation, the plastic flow in the thickness direction is updated based on the principle of isochoric plastic flow as Eq. (A14).

So far,all the iterations end and state variables are updated.It should be pointed out that in order to avoid the nonconvergence of the model implementation with the VUMAT code, the maximum number of Newton iteration step in the VUMAT is large enough for iterative convergence and the written code of complex formulas may split into some simple combination parts. Meanwhile, avoiding situations where the denominator of fraction may be zero for non-convergence.