Evasion guidance algorithms for air-breathing hypersonic vehicles in three-player pursuit-evasion games

Tin YAN, Yunli CAI,*, Bin XU

a School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China

b School of Automation, Northwestern Polytechnical University, Xi’an 710072, China

KEYWORDS Differential game theory;Game theory;Hypersonic vehicles;Optimal control;Pursuit-evasion strategy

Abstract In practical combat scenario, the cooperative intercept strategies are often carefully designed, and it is challenging for the hypersonic vehicles to achieve successful evasion. Based on the analysis, it can be found that if several Successive Pursuers come from the Same Direction(SPSD)and flight with a proper spacing,the evasion difficulty may increase greatly.To address this problem, we focus on the evasion guidance strategy design for the Air-breathing Hypersonic Vehicles(AHVs)under the SPSD combat scenario.In order to avoid the induced influence on the scramjet,altitude and speed of the vehicle,the lateral maneuver and evasion are employed.To guarantee the remnant maneuver ability, the concept of specified miss distance is introduced and utilized to generate the guidance command for the AHV. In the framework of constrained optimal control,the analytical expression of the evasion command is derived, and the constraints of the overload can be ensured to be never violated.In fact,by analyzing the spacing of the pursers,it can be classified whether the cooperative pursuit is formed. For the coordination-unformed multiple pursers,the evasion can be achieved lightly by the proposed strategy.If the coordination is formed,the proposed method will generate a large reverse direction maneuver, and the successful evasion can be maintained as a result. The performance of the proposed algorithms is tested in numerical simulations.

1. Introduction

With the rapid development of hypersonic vehicles, the strategy of evasion and pursuit in near space has become a hot research spot.1,2In the past decades,the advances of the hypersonic weapons have raised the rapid development of the abilities and strategies of pursuers.As a result,the difficulty for the hypersonic vehicles to achieve their attack tasks has been largely increased, and it is of significant importance to carry out the research upon the evasion strategies of the hypersonic vehicles.

The evasion strategies in Pursuit-Evasion (PE) games have received extensive research.3-12The optimal evasion strategy from proportionally guided missiles is proposed under the assumption of two-dimensional linearized kinematics. The analytical expression of the specific maneuver moment is provided, demonstrating that the maneuver switching times are related to the pursuer’s proportional guidance coefficient.3Considering the physical constraints of angular velocity and angle of attack, Raivio and Ranta4proposes an optimal three-dimensional avoidance trajectory. In recent years, the concept of evasion with the specified miss distance is firstly proposed,and meanwhile the minimum-effort-evasion strategy is developed with perfect information.5Moreover, there are many related literatures to study evasion strategies from different perspectives, and the optimal control theory and differential game method are used to construct the guidance laws.6-12However,the aforementioned results are all obtained based on the two-player PE games. In fact, if the single pursuer is not capable of achieving predefined tasks,two or multiple cooperative pursuers will be applied to pursue the target.In this case,the aforementioned evasion strategies maybe non-effective,and hypersonic weapons maybe intercepted lightly by the subsequent pursuer.

Recently, many researchers have taken intense interests in the evasion strategies from multiple pursuers.13-32Kelley13discusses some aspects of two-on-one team tactics. Bhattacharya and Hutchinson14analyze the two-on-one PE problem subject to visibility constraints, and meanwhile provide the schemes of constructing the initial pursuers configurations.The quadratic cost problem is investigated for the two-on-one linear PE games.15Furthermore, the linear differential game problem has also been discussed, and several cooperative strategies of two pursuers have been developed to reduce the miss distance.16,17As further development, a fixed-final-time cooperative pursuit strategy has been discussed.18Considering a nonconvex payoff of the distance between the evader and the two pursuers, the two-pursuer/one evader problem is analyzed.19Hagedorn and Breakwell20point out that if the evader possesses significant velocity advantage, the evader can pass the two pursuers directly.Aiming at the stochastic characteristics of the two-on-one PE games,several aspects have been discussed.21Just mention a few, some classical or novel results about multi-player PE games are shown,22-32which can also provide guides for our design, since the two-pursuer/oneevader problem is a subset of the class of evasion from a group of pursuers.

It should be noticed that, although fruitful evasion results have been achieved for two-on-one PE games,the combat scenario may be assumed too hypothetical for the hypersonic vehicles. In fact, in the existing evasion results, the multiple pursuers always come from different directions simultaneously.

However, because of the high-speed development of the hypersonic vehicles,the head-on pursuit33and the combat scenario of Successive Pursuers coming from the Same Direction(SPSD) will often be encountered in the future. In the SPSD combat scenario, the spacing ΔX between the pursuers is a key variable. If ΔX is carefully designed and within an appropriate range,the difficulty of successful evasion may be largely increased. When the evasion strategies13-21are applied, it is difficult to achieve successful evasion or maintain desired guidance performance. Therefore, for the purpose of achieving the attack task in the presence of SPSD combat scenario,it is necessary to develop the novel evasion strategies.

Motivated by the above observation,we focus on the novel evasion strategy design of the Air-breathing Hypersonic Vehicles(AHVs)under the SPSD combat scenario.Firstly,the evasion strategy with respect to two pursuers is proposed based on the game theory.Meanwhile,by using the constrained optimal control, the analysis formula of evasion strategy is derived.Different from the existing literatures, the proposed method considers SPSD combat scenario instead of the scenario where two pursuers are from different directions.Moreover,the proposed evasion strategy possesses hierarchical evasion mode,rather than simultaneous evasion in the existing literatures.13-21The main contribution of this paper can be summarized as follows:

(1) As far as the authors know, the strategy in this paper is the first evasion strategy for the hypersonic vehicles in the face of the SPSD combat scenario.

(2) In the SPSD combat scenario, even if the spacing ΔX between the pursuers is carefully designed,the proposed hierarchical evasion strategy can achieve desired guidance performance.

(3) Under this circumstance, the proposed strategy can guarantee the acceleration constraints of the AHVs to never be violated for the whole guidance process.

The rest of the paper is organized as follows. The SPSD combat scenario and the system model of PE games are described in Section 2. Then, the analysis of SPSD-faced hierarchical evasion strategy is provided in Section 3.Next in Section 4, the evasion guidance command is given based on the constrained optimal control. The numerical simulation results of SPSD combat scenario are shown in Section 5. Eventually,the conclusion is summarized in Section 6.

2. SPSD combat scenario and system model

The evasion-pursuit relationship and the definition of relative angles in horizontal plane (Remark 1) are shown in Fig. 1.The evader and pursuers are regarded as mass points.The subscripts E，Pi（i=1，2） indicate the state of the AHV and pursuers, respectively. All flight speeds VE，VPiare assumed to be constant,and the flight path varies with lateral accelerations aE，aPi, which are normal to velocity direction. aE，c，aPi，care guidance commands for the AHV and the pursuers, respectively.ridenotes the relative distance and θE，θPiare the trajectory deflection angles of the AHV and pursuers respectively.In order to ensure the robustness of the evasion strategy, more stringent evasion conditions are considered,e.g.,the time delay of the pursuer detection system is ignored.

Sun et al.33pointed out that in order to achieve effective pursuit for AHV, the head-on engagement scenario is necessary.On this basis,for the SPSD combat scenario in this paper(Remark 2), it is assumed that the AHV and two pursuers P1and P2are both on the X axis at initial time t0, with opposite moving directions.At the instant that P1has moved on the Xaxis by a distance ΔX, P2is launched. Besides, the kinematics equations of both sides can be linearized near the initial line of sight.

Fig. 1 Planar engagement geometry of three-player.

The kinetic equations of both sides can be established as follows:

To facilitate the analysis of the problem, the time to go is defined as

The energy consumption of the AHV during the evasion process is given by

In summary,the optimal evasion problem of SPSD combat scenario in this paper can be summarized as Problem 1.

Problem 1. On the basis of the three-player PE game model given by Eq. (11) and the guidance laws of pursuers given by Eq.(9),the evasion strategy should be derived to minimize the energy consumption given by Eq. (16) (Remark 5), while the miss distances subject to Eq. (14) and the control constraint subject to Eq. (15).

Remark 1. In this paper, the AHV chooses evasion in the horizontal plane. The reason can be concluded in the following: For the AHV,the sharp change of attitude angle and angular velocity will affect the working state of scramjet.35-38It is undesired for the evasion. Compared with longitudinal maneuver, lateral maneuver can be carried out at a fixed altitude and fixed speed to avoid the impact on the attitude angle and angular velocity due to changes in speed and altitude during evasion. Therefore,compared with longitudinal maneuver, the maneuver in the horizontal plane should be more appropriate for the evasion of the AHV.

Remark 2. The SPSD pursuit strategy may be often encountered in the future.Because of AHV’s high-speed characteristics,it is necessary for the interceptors to employ the head-on pursuit strategy for intercepting the AHV.27Meanwhile, cooperative pursuit for the AHV cannot be achieved if the multiple pursuers are from different directions.In fact,in the face of multiple pursuers coming from different directions,AHV can adjust its speed direction to guarantee the head-on situation with only one of the outermost pursuers,and the head-on situation with the other pursuers can never be formed.As a result,successful evasion can be achieved lightly. Hence, the SPSD pursuit strategy may be utilized by the AHV-faced interceptors.

Remark 3. In this paper, the concept of lower-bound-evasion is employed. It is known that hit-to-kill interception is necessary for the pursuit of the AHV.39In this paper,a variable M,which denotes the maximum distance satisfying the hit-to-kill requirement,is chosen as the lower bound of miss distance for successful evasion. Accordingly, we know that when≥M, AHV can achieve the goal of evasion with the boundary value of miss distance. This provides the basis for AHV to evade with minimum energy consumption.

Remark 4. There indeed exists physical constraints of the AHV’s acceleration.In the cruise stage of the AHV,the working conditions of scramjet are limited, and the strong coupling between engine and aerodynamic force limits the maximum usable angle of attitude, resulting in its acceleration being limited.35-38Therefore, the evasion strategy of the AHV must take the limitation of its acceleration into account.

Remark 5. In practical evasion tasks, it is necessary to guarantee that the energy consumption is minimized.In view of the disadvantage of AHV’s maximum maneuverability compared with the pursuers and the existence of the subsequent pursuer, AHV should start large acceleration maneuver with respect to the current pursuer as late as possible in the process of evasion. As a result, the reaction time of the subsequent pursuer can be reduced. This ability can be ensured by minimizing energy consumption.

3. Analysis of SPSD-faced hierarchical evasion strategies

3.1. Classification of different spacing between two pursuers

In the SPSD combat scenario, the spacing ΔX between two pursuers P1and P2is carefully designed and within an appropriate range to form cooperative pursuit.(ΔX can be seen as a constant. The reason will be listed in Section 4.2).

Before further discussion, there is the assumption:

Assumption 1. In this paper, the maneuverability (speed and maximum lateral acceleration) of two pursuers is the same.

According to the value of ΔX, there are three different situations:

(1) ΔX ≤C1. In this case, two pursuers (P1and P2) are so close that they can be treated as single pursuer by the AHV. The evasion from P1and P2can be done once for all and corresponding evasion command is written as u2a.

(2) ΔX ≥C2（C2＞C1）. In this case, two pursuers are too far to form cooperative pursuit. The evasion from P1and P2can be done repeatedly and corresponding evasion command is written as u2b.

(3) C1＜ΔX ＜C2.In this case,two pursuers form cooperative pursuit so that the evasion strategy from two cooperative pursuers is essential. The corresponding evasion command is written as u2c.

The value of C1and C2are determined by the maneuverability of the AHV and pursuers.The flow charts of calculating C1and C2are shown in Section 4.2. For different pursuers’maneuverability, the values of C1and C2may be different. A general processing method is described in Section 4.4.

3.2. Framework of evasion strategies and analysis

As can be seen from Section 3.1, two pursuers form cooperative pursuit only in Situation 3(C1＜ΔX ＜C2). Situations 1,2 can be equivalent to two-player PE game. Thus, the evasion strategy from single pursuer is necessary before further derivation.

In view of the disadvantage of AHV’s maximum maneuverability, the evasion strategy from single pursuer should be summed up as follows:

Evasion strategy from single pursuer: The AHV should keep the lateral acceleration command nearly at 0 in the early stage.At the end phase of the PE game,the AHV will perform a large single-side lateral maneuver to evade from the pursuer.The corresponding evasion command is written as uEP1.

On this basis,the evasion schematic diagrams of Situation 1(ΔX ≤C1)and situation 2(ΔX ≥C2)are shown in Fig.2.And the framework of evasion strategies in this paper is shown as Fig. 3.

Fig. 2 Evasion schematic diagram for Situations 1, 2.

4. Evasion guidance command

4.1. Evasion command from single pursuer uEP1

As shown in Fig.3,in order to derive the evasion strategy from two pursuers,the minimum effort evasion command uEP1from single pursuer is necessary.

In the process of deriving uEP1, the two-player PE game model can be obtained by removing the second pursuer of the three-player PE game model in Section 2.

In the previous work, the acceleration command is unbounded, and a minimum effort evasion strategy which makes the miss distance Z1（tf1）=M is proposed.5Differently,in consideration of bounded acceleration of the AHV,the new performance index is given by

where Q（Q ＞0） is a weighted parameter to be designed. The value of the parameter Q reflects the trade-off between the miss distance and the effort of the AHV. By adjusting Q, the miss distance is larger than the boundary value M while u meets the acceleration constraint.

As mentioned in Section 3, the AHV and the pursuer are both on the X axis at initial time t0, with opposite moving directions.As a result,there is Z（t0）=0.On this basis,considering the evasion condition inequality (14), the condition that Z1（tf1）≥M is chosen as the criteria of successful evasion.

According to Eq. (17), the evasion command uEP1can be expressed as

As the Evasion strategy from single pursuer which has been described in Section 3.2,on the basis of the AHV’s initiative of maneuver and the pursuer’s dynamics lag,it is conceivable that a sudden single-side maneuver of the AHV at the end phase of the PE game is bound to bring out an abrupt increase on the miss distance and the line of sight rate ˙λEP1. As a result, the guidance command v1（t） of the pursuer which is proportional to ˙λEP1will reach its maximum vmaximmediately.Therefore,an assumption about the guidance command of the pursuer can be given as follows.

Assumption 2. In the early stage of the PE game, the acceleration command v1（t） of the pursuer can be considered as 0. And at the end of the PE game, if the AHV generates a sudden single-side maneuver, the acceleration command v1（t）of pursuer can be considered as vmax.In other words,v1（t）can be considered as a constant value during the PE game process.

Assumption 2 is expressed into mathematical terms in Eq.(21) below.

For all pursuers whose guidance command v（t） is proportional to the line of sight rate ˙λEP1,also known as Proportional Navigation Guidance (PNG), Assumption 2 is tenable.Besides, a lot of advanced guidance laws in the PE game can be regarded as the derivatives of PNG.Therefore,the Assumption 2 is applicable for most PE scenarios.

In view of Assumption 2,the analytic expression of uEP1can be derived. Substitute command Eq. (18) into Eq. (11) yields

Fig. 3 Framework of evasion strategies.

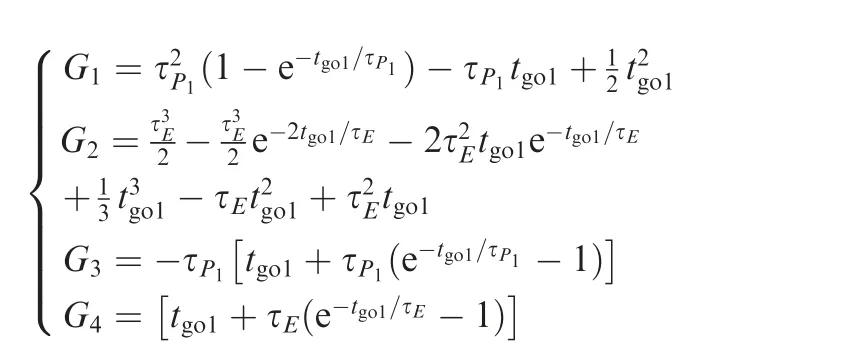
From Eq.(24),it can be summarized that the expression of the pursuer’s guidance law has no influence on that of AHV’s evasion command.For different guidance laws of the pursuer,command Eq. (24) of AHV is of minimum effort and can be applied to the situations whether the pursuer,s guidance law can be linearized. Therefore, command Eq. (24) is a general evasion command of AHV against pursuer with any known guidance law.With command uEP1,Evasion strategy from single pursuer can also be described as follows:

Evasion strategy from single pursuer: The AHV is able to achieve the evasion with guidance command Eq. (24). uEP1is pretty small that can be considered as 0 in the early stage of the PE game. At the end phase of the PE game, uEP1increases rapidly to accomplish the evasion.

4.2. Evasion commands u2a and u2b

Before derivation of u2aand u2b, there is a discussion on the value of the spacing ΔX between two pursuers.

As mentioned in Section 3.1,the value of ΔX can be seen as a constant before tf1. The reason is as follows:

According to Evasion strategy from single pursuer, the lateral maneuvers on Y axis of both sides occur at the end phase of the PE game.In consideration of the huge initial velocity of pursuers on X axis, the lateral maneuver in the end has little effect on pursuers’ speed on X axis. Besides, there is VP1=VP2in Assumption 1 in Section 3.1. From the above,the value of ΔX can be seen as a constant before tf1.

On this basis, the derivation of u2aand u2bis shown below.

For the situation ΔX ≤C1, the evasion schematic diagram is shown in Fig. 2. The evasion command uEP1of the AHV is executed at the initial time. And the value of uEP1will keep increasing until the maximum value umaxat the moment t1.After t1,the value of evasion command maintains at umaxuntil the end. In summary, the evasion command u2ais given by

where C is a constant with a large value so as to return the ballistic direction back to the initial direction as quickly as possible with the maximum acceleration.

On the basis of u2aand u2bunder the perfect information of the pursuers, the values of C1and C2are obtained by the way which is shown in Fig. 4.

C1is the maximum value of ΔX when the AHV achieve the evasion with command u2a.The idea of Fig.4(a)is to find out C1by gradually increasing the value ΔX in the simulation.The method of calculating C2in Fig.4(b)is similar to one in Fig.4(a)and is omitted here.In Fig.4(b),ΔXmaxis defined as the distance between the AHV and position P0on X axis at the moment tf1, which can be given by

In light of Fig. 4 the value of C1， C2will be obtained by simulation in Section 5.

4.3. Evasion command u2c

For the situation C1＜ΔX ＜C2that two pursuers form cooperative pursuit, the performance index can be selected as

According to the classification of ΔX in Section 3.1, when facing two cooperative pursuers, after the evasion from P1with uEP1,neither u2a(continuous positive maneuver with maximum acceleration)nor u2b(turning the ballistic direction back to the initial course and maneuver in positive direction again)can achieve the evasion from P2. Therefore, we can draw a conclusion that maximum acceleration in positive direction on the Z axis is not capable of evading from two cooperative pursues.

On this basis,the appropriate evasion command u2cshould be like this: after the moment tf1, the sign of the evasion command is switched at the right time. At the same time, for the pursuer P2, the value of guidance command v2keeps positive until yE＜yP2. During this period, AHV accumulated advantages of speed and displacement in Y axis negative direction(in other words, ˙yE＜˙yP2and yE＜yP2). Therefore, at the moment tf2, it is unable to achieve Z2（tf2）≥M, but Z2（tf2）≤-M is possible for the AHV.

From the above, the condition Eq. (14) for successful evasion can also be shown as

In summary, in the face of the two cooperative pursuers,command Eq. (30) is an optimal evasion command for the AHV. With command u2c, Evasion strategy from two cooperative pursuers can be summed up as follows:

Evasion strategy from two cooperative pursuers.The AHV is able to achieve the minimum effort evasion with guidance command Eq. (30). Before the moment tf1, there is u2c=uEP1.AHV maneuvers with command uEP1to evade from P1with the condition Z1（tf1）≥M. After tf1, the sign of u2cis switched at the right time to achieve the evasion from P2with the condition Z2（tf2）≤-M.

4.4. Evasion command with incomplete information

In summary,in the face of the two cooperative pursuers,command Eq. (30) is an optimal evasion command for the AHV.With command u2c, Evasion strategy from two cooperative pursuers can be summed up as follows:

In Section 4.2,with the perfect information of the pursuers,the values of C1and C2can be obtained by simulation.

When the information of pursuers is incomplete,the values of C1and C2are not easy to obtain directly. In this case, an evasion strategy, which can handle the case with incomplete information, is proposed in this section (is not related to the values of C1and C2, and applicable to any ΔX).

The corresponding performance index is given by

Remark 6. The major innovations of this paper

Compared with the existing literatures,3-21the major innovations of the proposed method are highlighted as follows.

(2) For the hierarchical evasion mode of AHV, the evasion strategy from P1is different from the evasion strategies from single pursuer.3-12The detailed difference is shown below: Some evasion strategies from single pursuer try to maximize the miss distance,3,4,7-12which leads to a large maneuver in the early time of the PE game and maybe intercepted lightly by the second pursuer in the SPSD combat scenario. Some evasion strategies from single pursuer try to achieve the evasion with a specific miss distance.5,6However, the miss distance constraint is regarded as an equality constraint.5,6Thus, It has excessive requirements for evader’s maximum acceleration and dynamic characteristics, which is not suitable for AHV for the reason of acceleration constraint. In this paper, the AHV achieve the evasion from P1with the boundary value M. Different from the previous works5,6, the miss distance constraint is regarded as an inequality constraint in this paper. This change reduces the requirement for evader’s maximum acceleration, and is suitable for the AHV.

Remark 7. Although several concepts and methods of minimum effort and specified miss distance have been discussed in the existing literature,the combat scenario and evasion mode in this paper are quite different from existing results and possess innovations. In fact, in the existing evasion results, the multiple pursuers are always coming from different directions simultaneously. In this paper, we consider the SPSD combat scenario,where several successive pursuers come from the same direction and flight with a proper spacing. As a result, the evasion difficulty may increase greatly. Under the SPSD combat scenario, a novel evasion strategy is proposed, possessing hierarchical evasion mode rather than simultaneous evasion in the existing literatures. Moreover, the evader has no teammate in this paper, while in the existing literature the evader has a teammate serving as a defender, and its evasion is achieved by cooperation with the defender.40In this paper, the evader has to achieve evasion from two pursuers by itself.

Remark 8. The rationality ofAssumption 1can be identified.Firstly, in reality, the USA has used two identical Pac-3 to achieve the goal of interception. Secondly, in theoretical research, a great number of references have assumed that the two pursuers have the same maneuverability.18,41-43Therefore,it can be known that Assumption 1 is acceptable and reasonable.Moreover,by using the proposed method,the guidance command is generated based on the actual ability of the interceptors.Even if the type and parameters of the interceptors changes, the proposed strategy can still be applied. Besides, considering real situation, the pursuers in this paper are assumed to possess strong enough maneuverability. For the pursuers with practical normal capacities,the proposed strategy can of course achieve successful evasion.

5. Simulation results

5.1. Simulation parameters and initial conditions

The basic parameters of both sides and simulation parameters of the engagement scenario in this paper are shown in Tables 1 and 2, respectively.

In Table 1, g is the gravity acceleration, a is the speed of sound.The value of |aPmax/g|is set as 8.0.In the existing literature,in order to meet the hit-to-kill condition for the pursuit,the maneuverability of pursuers should be more than three times the AHV’s acceleration.33For the sake of guaranteeing the robustness of evasion strategies in this paper, the value of|aPimax/g|is set as 8.0. And according to Assumption 1 in Section 3.1, the maneuverability of two pursuers is the same(VP1= VP2, aP1max= aP2max).

In Table 2, M is set as 1 m which is the maximum distance to meet the hit-to-kill condition. r0is set as 100 km due to the fact that pursuers can detect and track the evader within 100 km.

In the engagement scenario, the Augmented Proportional Navigation (APN) guidance law is selected as the guidance law of pursuers. The expression of APN is described as

5.2. Evasion from single pursuer

For the single pursuer, the AHV achieves the evasion with command uEP1in Eq. (24). The simulation results of evasion are shown as Fig. 5, and can be analyzed below:

(1) The flight trajectories of the AHV and the pursuer P1are shown in Fig. 5(a) (the lower part of the figure is a partial enlarged view of the upper part). That the miss distance y1（tf1）=1.03 m indicates that the evasion mission is successful.

Table 1 Basic parameters of AHV and Pi （i=1，2）

Table 2 Simulation parameters

Fig. 4 Flow chart of calculating C1， C2.

Fig. 5 Simulation results of evasion from single pursuer.

Fig. 6 Simulation results of evasion from two pursuers (ΔX ≤C1).

(2) The command acceleration uEP1is demonstrated by Fig. 5(b). At the end phase of the PE game, uEP1increases rapidly to accomplish the evasion. It is consistent with the Evasion strategy from single pursuer in Section 4.1.

(3) Two time points t1，tf1which will be discussed in later sections are marked in Fig. 6(b). t1（t1=32.74 s） is the moment that uEP1increases to the maximum value（umax=2g）. And tf1（tf1=33.50 s） is the terminal engagement time point.

Fig. 7 Simulation results of evasion from two pursuers (ΔX ≥C2).

5.3. Evasion from two pursuers

According to the different value of ΔX, the three-player PE game are divided into three situations: ΔX ≤C1,ΔX ≥C2（C2＞C1） and C1＜ΔX ＜C2. In Section 5.3, for the three situations, the evasion with command u2a, u2band u2care simulated in turn. And the analytic expression of u2a,u2band u2care given by Eqs. (25), (26) and (30).

5.3.1. Situation 1 （Δ X ≤C1）

For the situation ΔX ≤C1, the AHV achieves evasion with command u2ain Eq. (25). The following simulation consists of two parts: According (A) to Fig. 4(a), the value of C1is shown in Fig.6(a).(B) In order to observe the trajectory trend of the AHV,by setting ΔX=C1,the flight trajectory and miss distance of the AHV are demonstrated by Fig. 6(b)-(d).

It can be concluded that:

(2) The flight trajectories of the AHV and pursuers P1， P2are shown in Fig. 6(b) and Fig. 6(c). It can be seen that the miss distances y1（tf1）=1.03 m and y2（tf2）=1.03 m,thus the evasion mission is successful.

(3) The command acceleration u2ais illustrated by Fig.6(d)and is consistent with the analytic expression in command Eq. (25). At the end phase of the PE game, the value of u2akeeps increasing until the maximum value umaxat the moment t1(t1=32.74 s). After t1, the value of u2amaintains at umaxuntil the end to evade from P1and P2once for all.(4) According to Fig.6(c)and(d),the flight trajectory of the AHV is coincide with the evasion schematic diagram in Fig. 2(a).

5.3.2. Situation 2 （ΔX ≥C2（C2＞C1））

Fig. 8 Simulation results of evasion from two pursuers (C1 ＜ΔX ＜C2).

For the situation ΔX ≥C2, the AHV achieves evasion with command u2bin Eq.(26). The following simulation consists of two parts: (A) On the basis of Fig. 4(b), the value of C2is shown in Fig.7(a).For the parameter ΔXmaxin Fig.4(b),substituting tf1=33.50 s into Eq. (26) yields:ΔXmax≈VP1tf1=4×298.5 m/s×33.50 s ≈40.0 km (in this paper H=25.0 km, there is a=298.5 m/s). (B) In order to observe the trajectory trend of the AHV, by setting ΔX=C2, the flight trajectory and miss distance of the AHV are demonstrated by Fig. 7(b)-(d).

It can be concluded that:

(1) As shown in Fig. 7(a), similar to the analysis in Section 5.3.1, it can be seen that C2= 9.5 km.

(2) The flight trajectory of the AHV and pursuers P1and P2are shown in Fig. 7(b) (the lower part of the figure is a partial enlarged view of the upper part). The evasion is successful with y2（tf2）=1.07 m and y1（tf1）=1.03 m(On the basis of u2b=uEP1before tf1, the value of y1（tf1） is equal to the value of y（tf） in Section 5.2).

(3) As shown in Fig. 7(c), the trajectory deflection angle θE= 0°at the moment t2（t2=36.09 s）.

(4) On the basis of the value of tf1and t2, the command acceleration u2bcan be acquired and is illustrated by Fig.7(d),consistent with the analytic expression in command Eq.(26). After the moment tf1, the AHV swerves swiftly to make the trajectory deflection angle θE= 0°at the moment t2. After t2, the value of u2bincrease rapidly to achieve the evasion from P2.

(5) As can be seen from Fig.7(b)-(d),the flight trajectory of the AHV is coincide with the evasion schematic diagram in Fig. 2(b).

5.3.3. Situation 3 (C1＜ΔX ＜C2, two pursuers form cooperative pursuit)

In view of simulation results, C1= 2.7 km, C2= 9.5 km.When 2.7 km ＜ΔX（t）＜9.5 km, P1and P2form cooperative pursuit. For the situation that P1and P2form continuous threat, the AHV achieves evasion with command u2cin Eq.(30). The following simulation consists of two parts: (A) For different values of ΔX, the miss distance y2（tf2） is shown in Fig. 8(a) (On the basis of u2c=uEP1before tf1, the value of y1（tf1）≡1.03 m).(B) In order to observe the trajectory trend of the AHV, by setting ΔX=C1and ΔX=C2respectively,the flight trajectory and guidance command of the AHV are demonstrated by Fig. 8(b)-(d).

It can be analyzed that:

(1) As shown in Fig. 8(a), for the situation 2.7 km ＜ΔX ＜9.5 km, y2（tf2）＜-1 m and the evasion is successful(The fluctuation of the curve in a very small range is caused by the simulation step size).

(2) For ΔX =2.7 km and ΔX =9.5 km respectively, the flight trajectories of the AHV and pursuers P1and P2are shown in Fig.8(b)and 8(c)(the lower part of the figure is a partial enlarged view of the upper part).It can be seen that the miss distances y2（tf2）=-1.05 m and y2（tf2）=-1.08 m,thus the evasion mission is successful.

(4) As can be seen from Fig. 8(b)-(d), the flight trajectory and evasion command of the AHV is consistent with the Evasion strategy from cooperative pursuers in Section 4.3.

6. Conclusions

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by Aeronautical Science Foundation of China (No. 20160153002); National Natural Science Foundation of China(No.61933010);Aeronautical Science Foundation of China (No. 20180753007); Natural Science Basic Research Plan in Shaanxi Province, China (No. 2019JZ-08).