Coning motion instability of spinning missiles induced by the delay of strap-down seeker
Xiao HU, Shuxing YANG
a School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China
b Xi’an Modern Control and Technology Institute, Xi’an 710065, China
c Key Laboratory of Dynamics and Control of Flight Vehicle, Ministry of Education, Beijing 100081, China
KEYWORDS Coning motion;Dynamic stability;Proportional guidance system;Spinning missiles;Strap-down seeker
Abstract The strap-down seeker, which combines the seeker’s and the onboard gyro’s measurements to obtain the target information, has been extensively applied by spinning missiles. The response delay of the strap-down seeker, a novel factor that could result in crosscoupling between the acceleration commands in the pitch and yaw channels and subsequently cause the significant deterioration in dynamic stability of the spinning missile equipped with a rate loop,is noted in this paper.The sufficient and necessary stability conditions are also analytically established based on the system equation with complex coefficient, which are further verified by numerical simulations. It could be indicated that the response delay of the strap-down seeker will greatly deteriorate the dynamic stability of the whole guidance system designed by the conventional method. It is also noticed from analysis that the stable region of the combined guidance coefficient is shrunken significantly with the increase of the spinning rate.
1. Introduction
The coning motion stability of spinning missiles has received considerable research efforts in the past 10 years. Unlike the non-spinning missile, the continuous spinning of the airframe could lead to the cross-coupling effects between the pitch and yaw channels, which might potentially induce the coning motion instability.1-4Thus the separated channel method to design autopilots for non-spinning missiles could no longer guarantee the stability of the spinning ones. Based on this issue,Yan et al.5,6have analytically derived the stability conditions of spinning missiles with a rate loop and an attitude autopilot, and the proposed criteria was also verified by numerical simulation. Li et al.7,8investigated the coning motion of spinning missiles with the acceleration autopilot and the three-loop autopilot, and have analytically deduced the corresponding stability criteria.Furthermore,other factors in the autopilot loop,like hinge moment and backlash of servo system, could also have the impact on the coning motion stability, which have been investigated by Zhou et al.9,10
These above works mainly studied how the coning motion affects the design parameters of the autopilot for spinning missiles, but the proportional guidance loop containing various seekers was not taken into account. The serious coupling effects of spinning missiles could not only dramatically degrade the stability of the autopilot loop, but also the guidance loop. Considering the parasitic effect induced by the radome aberration of the radar homing seeker, the coning motion stability of spinning missiles with different autopilots has been studied.11,12Hu et al.4have investigated and established the stability conditions of spinning missiles only employing the proportional guidance loop,where the platform seeker is applied to obtain the target information Moreover, the strap-down seeker, rigidly attached to the airframe, has also been widely adopted by spinning missiles to obtain the target information due to its advantages in cost reduction and structure simplification.13-15He et al.16regarded the strap-down seeker as a proportional term,and proposed the coning stability criteria for the proportional guidance system of spinning missiles when considering the parasitic loop induced by the scaling factor error.
Nevertheless, different from the platform seeker studied in Ref. 4, the strap-down seeker must integrate its measurement with the onboard gyro’s measurement17,18to obtain the lineof-sight angular rate information. Thus, in term of strapdown seekers applied to the spinning missiles, such as phased-array strap-down seekers15and strap-down imaging seekers,13their response delay could inevitably induce the novel coupling effect in the measurement of the sight angular rate in two channels, which would further cause the overload commands cross-coupled. The coupling effects induced by response delay of the strap-down seeker might potentially induce a coning motion instability, even though the autopilot for spinning missiles is designed according to the stability boundary criteria given by Yang et al.5-8However, there has been limited research attention given to the stability of the whole proportional guidance loop for spinning missiles equipped with a rate loop when considering the impact of response delay of the strap-down seeker, and the corresponding dynamic stability criteria has still not been deeply explored till now.
The present paper aims to investigate and establish the stability criteria of the spinning missile employing a proportional guidance law and a rate loop, when considering the response delay of strap-down seekers. The dynamic equations of the strap-down seeker with response delay are derived in the non-spinning body coordinate system. Neglecting the nonlinear items,the whole guidance system equation with complex coefficients can be generated.Subsequently,the coning motion stability criteria are deduced analytically and then verified through numerical simulations.It is observed that the response delay of the strap-down seeker induces the coupling effect between the acceleration commands in the pitch and yaw channels, and then degrades the design parameters stable region of the whole guidance system. Furthermore, the stable region is decreased significantly with the growth of the spinning rate.
2. Basic problem formulation
In this work, the canard-control spinning missiles equipped with a strap-down seeker are investigated.Unlike the platform
seeker, the strap-down seeker rigidly attached with missile body could only measure the error angular rate between the line of sight and the longitudinal axis of the body. The geometry of the missile-target relative motion in the longitudinal plane could be illustrated in Fig. 1, where, qyrepresents the sight angle with respect to the inertial ground coordinate system, θ denotes the pitching angle as mentioned above, εyis the error angle between the line of sight and the longitudinal axis of the missile, xs, xnand xgare aligned with the Line of sight, the longitudinal axis of missile, and the x-axis of the ground coordinate system respectively. According to Fig. 1, the longitudinal sight angular rate obtaiand true error sight angular ratesned by the strap-down seeker can be given as
When taking the response delay of the strap-down seeker into account, the rolling of the airframe could inevitably cause coupling effect between true error sight angular rates and measured ones in non-spinning body coordinate system. This coupling effect in sight angular rates definitely make the overload commands cross-coupled and then result in the dramatic deterioration of the coning motion stability. The coupling effect caused by the response delay of the seeker will be modelled and the stability of whole guidance system will be analyzed in following sections.

Fig. 1 Geometry of the missile-target relative motion.

Fig. 2 Proportional guidance loop for a spinning missile with strap-down seeker.
3. Mathematic model
3.1. Mathematic model of the strap-down seeker with response delay



3.2. Servo commands generation

To simplify the derivation of dynamic stability for spinning missiles,the system inputs of sight angular rates,i.e. ˙qyand ˙qz,could be assumed to be zero, and then the servo commands coupled in two channels could be simplified as
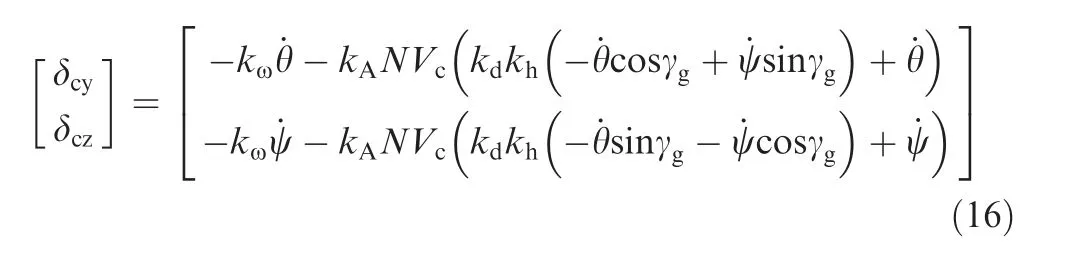
3.3. Command resolution and actuators during spinning motion
Despite the constant input commands,the spinning motion of the airframe could induce harmonic responses in the control surface angles. The actuator system can be considered as a second-order system. Its natural frequency and damping ratio are 1/Tsand μsrespectively.Moreover,the signal propagation delay τ1is also considered.Therefore,the relationship between the inputs and outputs of the servo in the non-spinning body coordinate system can be obtain as5:

3.4. Equations for the airframe motion
According to the modelling methods of Murphy2and Zipfel,22the translational and rotational motion of the spinning missiles are usually described in the non-spinning body coordinate system Oxnynznas shown in Fig. 3. It could be assumed that the flight velocity and spinning rate are constants,and then the lateral dynamics equations for the spinning missile can be expressed as:

Fig. 3 Definition of the non-spinning body coordinate system.
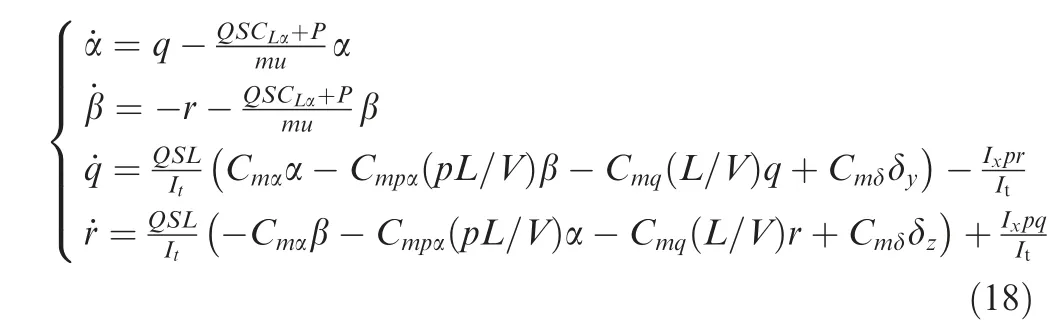
where, p, q and r are roll, yaw and pitch angular rates of airframe respectively; α and β are the attack angle and sliding angle in the non-spinning body coordinate system; Ixand Itrepresent the moments of inertia with respect to the longitudinal and lateral axis respectively;S and L are the reference area and length respectively,CDand CLαdenote the drag coefficient and the lift coefficient slope; Cmα,Cmδ,Cmqand Cmpαare the coefficients of the static moment, the control moment, the lateral damping moment and the Magnus moment respectively;Q is the dynamic pressure.
4. Stability conditions
The variables ψ, θ and ˙ψ can be assumed as small values throughout the practical terminal guidance stage,. Therefore,as indicated in Fig.3,the attitude angular velocity of airframe in the non-spinning body coordinate system, p,q,r[ ]T, can be expressed as

Apparently, it is an analytical solvable second-order complex differential equation, and its characteristic equation can be further obtained as:

As the sufficient and necessary dynamic stability condition,the above inequalities Eq. (26) indicate that the guidance system of the spinning missile with the strap-down seeker and the rate loop could be convergent only when all the design parameters satisfy certain conditions simultaneously.
5. Discussion on stability conditions
5.1. Case without response delay of the strap-down seeker
In this case, it is assumed that there are no steady errors and phase lag in the dynamic response of the strap-down seeker,i.e. K2=1 and γg=0. Consequently, the servo commands could be only determined by the rate feedback loop, and the characteristic parameters can be simplified as p1=a1-b21+b3K1kωcosγt, q1=-b22+b3K1kωsinγt, p2=-b11-a1b21+a1b3K1kωcosγtand q2=-b12-a1b22+a1b3K1kωsinγt.The stability criteria Eq. (26) can be written as
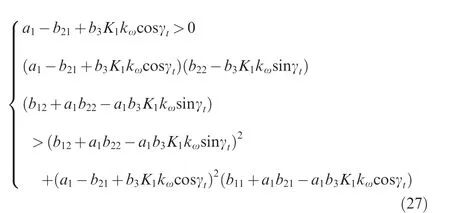
Without considering the dynamic model of the strap-down seeker, the guidance part produces no coupling effect to the acceleration commands. Thus the lift coefficient, thrust force as well as the translational motion of spinning missiles can be neglected,i.e.a1=0,and then Eq.(27)can be further simplified as

Overall, the stability criterion described in inequalities Eq.(28), are basically identical to those obtained in Refs. 5,7 for the spinning missile with a rate loop.
5.2. Case under the impact of the response delay of the strapdown seeker
When the response delay of the seeker is considered,the crosscoupling effect has been introduced into the acceleration commands, which causes the significant difference in the stability conditions. The stability criteria could be described as Eq.(26), where the characteristic parameters are determined by Eq.(24)and Eq.(25).Because the low-speed spinning missiles have relatively small Magnus moment and Gyroscopic moment terms, they can be neglected in the stability analysis,i.e.b12=0 and b22=0.Moreover,the relatively smaller time constant of the strap-down seeker Tdand the low spinning rate determine that the dynamic gain of the seeker can be assumed as kh=1, and the delay angle of the seeker γgcould be regarded as a small value. Thus, cosγg=1 and sinγg=γgcan be obtained. By neglecting the small value a1b21, then Eq.(24) and Eq. (25) can be simplified as:

It is observed from Eq. (32) that the response delay of the strap-down seeker could cause the coupling effects of the acceleration commands between pitch and yaw channels, and then degrade the stable region of parameters for the autopilot loop,while the coupling effects of the servo are not taken into account.
Moreover, when all the coupling effects in the whole guidance system are considered,the coning motion stability conditions could be further analyzed as follow.
As is commonly done in practice, the total delay angle of actuator could be limited under 90°.Thus in the next discussion,it is assumed that the total delay angle of servo γtis less than 90°. The first inequality can obtain an upper bound

Since a1-b21>0,the upper limit obtained in Eq.(33)could not satisfy the second inequality, which means that the stability conditions given in Eq. (31) are mainly determined by the second inequality. The second inequality in Eq. (33), also the stability condition, could be transformed as

the second inequality can be definitely satisfied. Thus Eq. (35)could be the sufficient condition for the dynamic stability.Based on the monotonicity of, its range can be given through combining Eq. (33) and Eq. (35)


Fig. 4 Gain of rate loop kω and stable region of combined guidance coefficient.
In terms of the spinning rate, when it increases, the phase lag angle of the servo system γtis also improved.It is observed from Eq. (36) that a higher γtdetermines a smaller sloping of these two linear functions, 1/kAtanγt, which further means, the upper bound of, gets reduced and the stable region also gets dramatically shrunk. Meanwhile, the increase of spinning rate also results in a larger lag angle of the strap-down seeker γg.Therefore, as the spinning rate of the airframe increases, the stable region ofwould be shrunk greatly.
6. Simulation verification and analysis
Choosing a certain forward gain kA =0.007,the upper limits of the combined guidance coefficient for cases with different values of spinning rates are calculated based on nonlinear models, and the results could be used to make a comparison with the limits obtained by the analytical stability criteria.Table 2 shows the calculated upper limits of linear model[N (- Vc)]Land nonlinear ones [N (- Vc)]NLrespectively. Itcould be clearly indicated that, with different spinning rates,all the relative errors between these two models are not beyond 3.5%. Moreover, the upper limit ofobtained by proposed stability criteria is relatively conservative. Therefore, in the derivation of the coning motion stability criteria for spinning missile under the impact of response delay of the strapdown seeker,the linear model mentioned above could be available.And the comparison in Table 2 can illustrate the applica-bility of the derived inequalities (26) in the practical engineering.

Fig. 5 α and β in the stable state, N(-Vc)=300.
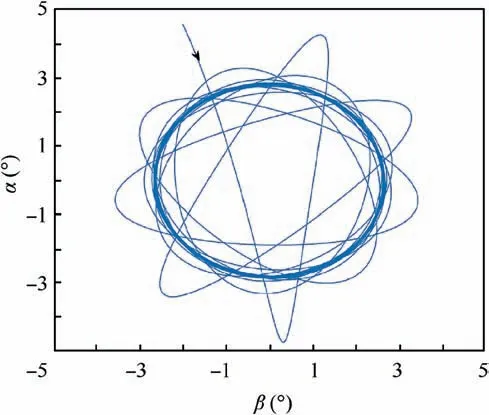
Fig. 6 α and β in the critical stable state, N(-Vc)=400.69.

Fig. 7 α and β in the unstable state, N(-Vc)=500.

Table 2 Stability limits at different spinning rates with linear and nonlinear model.

Table 3 Stability upper limits of N -Vc( )with different seeker time constants.


Fig. 8 Stable region of the combined guidance coefficient.

7. Conclusions
The measured sight angular rates in pitch and yaw channels of the spinning missile would get cross-coupled due to the response delay of the strap-down seeker, which could cause the coupling effects of the overload commands and then the dramatic deterioration of the coning motion stability. In this paper, the actual output equations of the strap-down seeker with response delay in the non-spinning body coordinate system are formulated,and the sufficient and necessary conditions for the coning motion stability of the spinning missile with the strap-down seeker and a rate loop are further established.From the proposed analytical stability conditions, it can be found that the stable region of the combined guidance coefficient is reduced dramatically as the spinning rate grows, while its upper limit could be improved with the increase of the rateloop gain, which has been further verified by the numerical simulations. It is also revealed that the novel coupling effect induced by the response delay of the strap-down seeker could greatly degrade the stable region of parameters of the spinning missile guidance system. Moreover, the comparison in the upper limit between the linear and nonlinear model could illustrate the adaptability of the proposed method in practice.Thus the stability criteria given in this article could be employed to the engineering design of the guidance system for spinning missiles with the rate loop and the strap-down seeker.
Acknowledgments
The authors gratefully acknowledged the financial support from National Science Foundation of China (No.11532002).
 CHINESE JOURNAL OF AERONAUTICS2020年12期
CHINESE JOURNAL OF AERONAUTICS2020年12期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Design and experimental study of a new flapping wing rotor micro aerial vehicle
- CFD/CSD-based flutter prediction method for experimental models in a transonic wind tunnel with porous wall
- Prediction of pilot workload in helicopter landing after one engine failure
- Study of riblet drag reduction for an infinite span wing with different sweep angles
- Modulation of driving signals in flow control over an airfoil with synthetic jet
- Strong interactions of incident shock wave with boundary layer along compression corner
