Lightweight hybrid visual-inertial odometry with closed-form zero velocity update

QIU Xiaohen, ZHANG Hai,*, FU Wenxing

a School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China

b Science and Technology on Aircraft Control Laboratory, Beijing 100191, China

c Science and Technology on Complex System Control and Intelligent Agent Cooperation Laboratory, Beijing 100074, China

KEYWORDS Inverse depth parametrization;Kalman filter;Online calibration;Visual-inertial odometry;Zero velocity update

Abstract Visual-Inertial Odometry(VIO)fuses measurements from camera and Inertial Measurement Unit(IMU)to achieve accumulative performance that is better than using individual sensors.Hybrid VIO is an extended Kalman filter-based solution which augments features with long tracking length into the state vector of Multi-State Constraint Kalman Filter(MSCKF).In this paper,a novel hybrid VIO is proposed, which focuses on utilizing low-cost sensors while also considering both the computational efficiency and positioning precision. The proposed algorithm introduces several novel contributions. Firstly, by deducing an analytical error transition equation, onedimensional inverse depth parametrization is utilized to parametrize the augmented feature state.This modification is shown to significantly improve the computational efficiency and numerical robustness, as a result achieving higher precision. Secondly, for better handling of the static scene,a novel closed-form Zero velocity UPdaTe (ZUPT) method is proposed. ZUPT is modeled as a measurement update for the filter rather than forbidding propagation roughly, which has the advantage of correcting the overall state through correlation in the filter covariance matrix. Furthermore, online spatial and temporal calibration is also incorporated. Experiments are conducted on both public dataset and real data.The results demonstrate the effectiveness of the proposed solution by showing that its performance is better than the baseline and the state-of-the-art algorithms in terms of both efficiency and precision.A related software is open-sourced to benefit the community.①https://github.com/PetWorm/LARVIO

1. Introduction

Fusion of visual and inertial measurements is a popular topic recently.Solutions to such problem are able to provide estimation regarding both the positioning as well as the surrounding environment at the same time.This kind of algorithms are termed as Visual-Inertial Simultaneously Localization And Mapping (VI-SLAM). Exploration have been done to use VISLAM in navigation on planetary rover.1Other potential applications include localization of Unmanned Aerial Vehicles(UAVs), augmented reality and driverless cars. It also turns out to be an efficient complementary navigation solution in environments without access to global information such as Global Navigation Satellite System (GNSS) signals.

VIO is a subset of VI-SLAM problem, which mainly concentrates on positioning rather than building a consistent map of surrounding. As the commercial devices such as cellphones or UAVs generally use low-cost sensors, researchers tend to focus their efforts more on building algorithms for such applications. The frameworks of visual inertial fusion problem are mainly divided into two main branches namely the filter-based and optimization-based approaches.2So far,due to their iterative mechanism,the optimization-based methods are widely recognized as better than filter-based methods in terms of precision.3However, the computational efficiency still remains a concerned issue in optimization-based methods.Even though the computation costs can be reduced by leveraging a sparse matrix factorization,4optimization-based VIO systems still need to be tailored sometimes in order to be deployed on a computation-limited platform. This adaptation usually leads to downgraded performance.5

Filter-based methods dominated VIO solutions before the flowering of optimization-based methods. In this category,MSCKF, an algorithm based on Extended Kalman Filter(EKF), outperforms all other filtering techniques in terms of both precision and computational efficiency.6It is outstandingly efficient and hence much suitable to be deployed on low-cost devices.This is achieved by marginalizing out features in the measurement residuals and keeping a sliding window of past camera or IMU poses in the filter state. Due to its superiority,vast follow-up works have emerged to improve the system performances under MSCKF framework.

Li and Mourikis7proposed a closed-form IMU error state transition equation and applied First Estimate Jacobian(FEJ)to correct the observability properties of MSCKF.Hesch et al.8applied an alternative Observability-Constrained Kalman Filter(OC-KF)method to correct the observability properties.Li and Mourikis9incorporated camera-IMU extrinsic parameters into the filter state, making the online spatial calibration possible, and formally publicized their work as MSCKF 2.0.

A vast amount of literature has been focused on enhancing the applicability of MSCKF. In order to deal with the temporal misalignment of IMU and camera data,time offset calibration was included into MSCKF by assuming a constant linear and angular velocity between consecutive image frames.10The aforementioned online temporal calibration problem is analyzed and shown to have a locally identifiable property for the time offset, except for several degenerate cases.11Li et al.12,13took into account the rolling-shutter effect, hence also making MSCKF applicable to commercial devices with rolling-shutter cameras.Fang and Zheng14used trifocal tensor to construct the measurement residual,and applied Unscented Kalman Filter (UKF) to improve the robustness and speed of the initialization procedure in MSCKF.In this paper,the proposed algorithm inherits some of the practically wellperformed enhancements, including camera-IMU spatial and temporal calibration, and using FEJ to correct the observability properties.

Since non-iterative filter-based methods are vulnerable to visual outliers, several research articles have worked on the visual front-end to improve the performance of MSCKF.Zheng et al.15used photometric error of patches around image features instead of geometric reprojection error as measurement residual. Sun et al.16expanded OC-KF to stereo camera rig and released its implementation as open-source. Although stereo cameras improve the robustness of a VIO system by providing an extra scale constraint, it would fail in feature matching process in case of brightness inconsistency.16Zheng et al.17introduced line features into stereo MSCKF by taking advantage of geometric constraints of the environment. Zou et al.18applied Atlanta world assumption to utilize the constraints of horizontal and vertical lines in man-made environment. Qiu et al.19demonstrated the statistical difference between matched and unmatched ordinary feature pairs, and used feature descriptors to eliminate outliers from results of sparse optical flow tracking. The proposed algorithm utilized the descriptor assisted optical flow tracking in the visual front-end,as well as the IMU error state propagation equation proposed in aforementioned reference.

Under traditional MSCKF scheme, information regarding features having a tracking length longer than the sliding window size would be partly wasted. This is because it preserves a sliding window of limited size and any observations exceeding the window size would either be dropped or used too early.6Li and Mourikis20proposed hybrid VIO to combine MSCKF with EKF based VIO. Features with long tracking lengths thus will be augmented into the filter state while other features would be used in MSCKF measurement update. This strategy is capable of utilizing complete constraints of features with long tracking length and thus improves the performance.In this case, a Three-Dimensional (3D) Inverse Depth Parametrization (IDP) was applied to parametrize the augmented features. Li et al.21improved the hybrid VIO by performing online self-calibration, and parameters including camera intrinsic parameters,rolling shutter effect,IMU intrinsic parameters, camera-IMU extrinsic parameters and time offset were incorporated into the filter state. Wu et al.22reformulated hybrid VIO by a square root inverse filter. This algorithm can run very fast on storage-limited platforms since it enables using single-precision number to code the algorithm.3D position in the world frame was applied to parametrize the augmented features, which consequently avoided covariance propagation in original hybrid VIO.However,3D Cartesian parametrization of features is considered to be inferior to 3D IDP, since the latter has a higher degree of linearity.23

3D IDP was introduced first in visual SLAM for providing a desirable Gaussian uncertainty of the feature state.23However, since there are usually numerous features being tracked in a SLAM system, the state dimension would become very large if using a 3D presentation, resulting in a cumbersome computation for real-time applications. Some visual SLAM or VI-SLAM adopted One-Dimensional (1D) IDP,24-26which uses pose of the host camera and a single parameter, the inverse depth, to model the feature position. In this case, the reprojection error in the host image is discarded,while obtaining higher computational efficiency and numerical robustness in exchange. When host camera of a feature drops out of the sliding window, the inverse depth propagation should be applied to find a new host. In this situation, an analytical expression can be easily obtained when using 3D IDP,20which is not quite straightforward for 1D IDP. Optimization-based VIOs usually do not need to deal with the 1D IDP propagation since they do not preserve a covariance as in EKF. Engel et al.24presented an expression of 1D IDP propagation,which is an analytical translation based on utilizing epipolar search for image patches matching. However, the given propagation formula is under the assumption of small rotation and it did not consider the error of all the relevant state. The proposed algorithm is based on hybrid VIO, while the 1D IDP was applied for augmented features which highly improve the computational efficiency and robustness. Moreover, an analytical inverse depth error propagation equation is proposed to deal with the covariance propagation when changing host frame,and this formula considered the error of all the relevant state.

ZUPT is commonly used in pedestrian navigation,trying to restrain the propagation error in low-cost Inertial Navigation System (INS).27,28Methods for detecting static scenes are therefore mostly based on IMU measurements.29For EKFbased VIO algorithms without static scene detection, the INS propagation would still be working while the stationary scene cannot provide effective measurement update.In this scenario,IMU measurement errors might lead to biased propagation and result in divergence. Few VIO solutions have considered dealing with this situation. Huai and Huang30identified the static scene by IMU data in their released code, where INS propagation is simply stopped if the static scene is detected.Qiu et al.19proposed a static scene detecting method based on image features and used stationary IMU data to initialize the filter state. In proposed algorithm, the static scenes are detected based on image features,and the ZUPT is introduced into the system as a closed-form measurement update by using static motion constraints.This strategy is capable of correcting states which resulted in biased propagation,including velocity,rotation and IMU biases.

Table 1 summarizes the features and properties of several representative VIO solutions mentioned above.

As an optimization-based solution, VINS-MONO has the highest precision,while it requires relatively high computation cost.The hybrid VIO with 3D IDP requires extra computation to deal with the augmented features, compared to the pure MSCKF and R-VIO.None of the solutions deal with the static scene except for R-VIO, while the strategy that it used is to simply stop propagation, and the static constraints are not fully utilized.All of the solutions are capable of online sensors parameter calibration.

In this paper, a novel EKF-based hybrid VIO algorithm is presented in detail,giving consideration to both computational efficiency and localization precision. The fundamental mechanism of hybrid VIO is based on MSCKF,and it is further characterized by augmenting features with tracking length larger than the sliding window size into the system state.Augmented features are parametrized by 1D IDP, which is a novelty in hybrid VIO or MSCKF algorithms. Furthermore, this is supported by the derivation of an analytical error propagation equation of inverse depth considering the overall state error for host frame changes. This perfection evidently increases the computational efficiency and numerical robustness.Besides,a novel method is proposed modeling ZUPT as an elegant closed-form measurement update in which the residual is constructed by not only zero velocity, but also the pose constraint between consecutive static images. In addition, FEJ is utilized to improve the estimator consistency, camera-IMU extrinsic parameters (including relative rotation and translation between coordinate frame of two sensors)and time offset between sensors’ timestamps are included in the estimator to further improve the performance.Experiments were conducted on both public dataset and real data. The results demonstrate the effectiveness of the proposed VIO solution as it outperforms the 3D IDP baseline and the state-of-the-art algorithms in terms of both efficiency and precision and that the proposed ZUPT method is able to utilize the static scene to further improve the algorithm performance.

The rest of this paper is organized as follows.Section 2 presents the conventional routine of the proposed hybrid VIO in detail. This includes the system and measurement model, and the proposed 1D IDP propagation formula. Section 3 introduces the closed-form ZUPT measurement update, and its integration logic within the conventional routine. Section 4 presents the experimental results and analyses.Finally,conclusions are made in Section 5.

2. Conventional routine of proposed hybrid VIO

In this section, the conventional routine of the proposed hybrid VIO is presented, including state definition, state transition equation, covariance management, feature-based measurement update and 1D IDP propagation for augmented features. Formulas for the proposed closed-form ZUPT and the logic of its integration into the conventional routine will be introduced in Section 3.

Fig. 1 presents the scheme of the conventional routine of the proposed algorithm. Novelties are colored in red, main loop is colored in blue,and other traditional portions in hybrid VIO are colored in black.

The proposed hybrid VIO is generally an EKF based algorithm,so the main process is a basic propagation and measurement update loop (colored in blue in Fig. 1). The system and filter state definition and state propagation equations are listed in Section 2.1, and relevant formulas are Eqs. (1)-(12). The measurement residuals for measurement update are introducedin Section 2.3.The expression of general state correction is presented by Eq. (23). In hybrid VIO, features for measurement update are classified into MSCKF features and augmented features. Residual and Jacobians of MSCKF features are presented in Section 2.3.2 by Eqs. (20)-(22), and there is no difference between them and traditional ones except for using Hamilton quaternion. In proposed algorithm, the augmented features are parametrized by 1D IDP,which is one of the main contributions of this paper, and the relevant contents are colored in red in Fig. 1. The initialization of augmented features are presented in Section 2.2.2 by Eqs. (14)-(16), and the measurement residual formulas and Jacobians are listed in Section 2.3.1 by Eqs. (17)-(19). Readers can refer to the work of Mourikis and Roumeliotis6for other basic formulas of MSCKF. As an extension of MSCKF, covariance management is necessary. The management of covariance about sliding window poses is of the traditional way as in the work of Li and Mourikis,7while for augmented features,1D IDP propagation considering all the relevant state error is proposed in this paper in case of host frame changes. This novelty is highlighted in red color in Fig.1.Details of the covariance management operations when augmenting and pruning states are presented in Section 2.2. Fig. 2 displays aforementioned operations in a graphical representation. Note that, Fig. 1 only illustrates the main portions in the proposed algorithm, which is aimed to distinguish the contributions from traditional algorithm.

Table 1 Features and properties of state-of-the-art VIO solutions.

Fig. 1 Scheme of conventional routine of proposed algorithm.

2.1. Filter state definition and transition equation

The proposed hybrid VIO is based on error state EKF,whose filter state is defined as the differences between the estimated system state and the true system state.Since the group of rotation is not a linear space, the symbol ⊕is used to represent a general ‘additional’ calculation for all the states. The relationship among error state,estimated system state and true system state is then given by

where x, ^xand δx denote true state, estimated state and error state respectively.

In hybrid VIO, system state x can be divided into three parts:

where xlegrepresents the legacy state, including current IMU pose, velocity, IMU biases, camera-IMU extrinsic parameters and time offset;xposrepresents the augmented poses state,consisting of a sliding window of past IMU poses with size N at most; xaugrepresents the augmented features state, containing M features being tracked currently with tracking length larger than N.

Since low-cost IMU cannot detect the earth rotation, the static world assumption is employed. The navigation results are calculated with reference to a fixed horizontal coordinates system, which is defined as world frame. The world frame can thus be regarded as an inertial frame ignoring the earth’s rotation.As a result,system state is propagated by a simplified INS integration,and the estimated error state is used as feedback to correct the propagated value.

The exact definition of these three parts of state and their error state transition equations are introduced as below.

2.1.1. Legacy state

The legacy state is listed as

Fig. 2 Changes in covariance matrix when augmenting or pruning IMU pose and features.

2.1.2. Augmented poses state

Every time a new image comes in, the corresponding IMU poses will be obtained by INS propagation and then be augmented into the system state. The number of augmented IMU poses is limited to N. As time goes by, a sliding window saving N past IMU poses is preserved in system state.

2.1.3. Augmented features state

For features whose tracking length surpasses the sliding window size N, their positions will be augmented into the system state. Li and Mourikis20and Wu et al.22applied 3D parametrization for augmented features in hybrid VIO. However in this paper,one of the contributions is utilizing 1D IDP to model augmented features, which lead to computation cost reduction and numerical robustness enhancement. To further guarantee bounded computation, the maximum number of augmented features is set to M. If more than M features meet the requirement, M features with the longest tracking length will be augmented into the state, and others would be used as MSCKF features.

The state of augmented features is

The initialization and error propagation equation of 1D IDP features will be presented in Section 2.2.2 and Section 2.4 respectively.

2.2.Covariance management for state augmentation and pruning

State augmentation and pruning would change filter’s covariance matrix accordingly. Fig. 2 gives a schematic explanation of these changes. Details are presented below.

2.2.1. Augmentation and pruning of IMU poses

Augmentation and pruning of IMU poses are standard procedures in MSCKF or hybrid VIO. As mentioned in Section 2.1.2,the current IMU pose will be augmented into filter state after INS and covariance propagation.Corresponding covariance matrix evolution is shown in Fig. 2(a), new blocks are calculated by matrix multiplication between a Jacobian Jpand predicted covariance Pk+1|k.Following Eq.(2)and Eq.(4),Jpcan be obtained as

where n and m are current number of IMU poses in sliding window and augmented features respectively.

If the size of sliding window surpasses N, the oldest IMU pose would be pruned from sliding window, after the conventional measurement update. This operation may also trigger MSCKF measurement update, if features observed by pruned poses have not been initialized yet.6The corresponding blocks in covariance matrix would be deleted afterwards,as shown in Fig. 2(b).

2.2.2. Augmentation and pruning of features

If the tracking length of a feature reaches N, it would be augmented into the state vector.The covariance matrix would also be changed accordingly. Li and Mourikis20presented detailed methods for this operation by using 3D IDP. In this section,the process for 1D IDP is presented.

The initialization procedure of a feature in 1D IDP is as below. Let fjbe a feature to be augmented. After INS and covariance propagation, the feature position is triangulated by nonlinear least-square minimization.6Since current IMU pose has not been corrected yet, only N-1 observations of fjwould be used in this process. The result of triangulation is the feature position under the second newest camera frame,which is regarded as the first host camera frame of fj.

After initialization, covariance of δρjand its crosscorrelation with other filter state should be added into overall covariance matrix, as shown in Fig. 2(c). An analytical formula can be obtained, to avoid initializing the covariance of δρjas a very large quantity approximating infinite,as proposed by Li and Mourikis.20

Fig. 3 Inverse depth initialization by correcting observation.

As shown in Fig.2(d),operations for managing covariance matrix when pruning a lost feature are relatively easy: first,locate the position of the lost feature in covariance matrix,and then delete the corresponding diagonal block and its cross-correlation with other filter states.

2.3. Measurement update

Three kinds of feature residuals will be used for conventional measurement update in hybrid VIO:MSCKF feature residual,old and new augmented feature residual. In this section, the detailed Jacobian of the measurement residual is presented along with the general expression of filter state correction.

2.3.1. Augmented features residual

Augmented features utilized 1D IDP in this paper,which is different from traditional hybrid VIOs. The detailed mathematical expressions of residual and Jacobians are presented in this section.

Residuals of old and new augmented features all stem from the reprojection error under unified camera coordinate. An elaborate linear model of residual about feature fjobserved by the kth image is presented as

2.3.2. MSCKF features residual

The residuals of MSCKF features are processed under the traditional routine: first marginalize out the 3D feature position pwfjfrom stacked residual of feature fj,and then apply the nullspace projection to reduce the dimension of stacked marginalized residual of all MSCKF features6.

The only difference here is that the unprocessed residual is partially related to the error of time offset,which is due to the temporal calibration method that is utilized.31

To distinguish from symbols in Eq. (17), T terms are used here to represent Jacobians of MSCKF residual. Detailed expressions are listed below:

For details of the marginalization and nullspace projection conducted on residual in Eq. (20), please refer to the work of Mourikis and Roumeliotis6

2.3.3. General state correction

In general case,three kinds of feature residuals will be blocked and utilized during measurement update: MSCKF features residual, old augmented features residual and new augmented features residual. The blocked residuals are processed by rectangular projection, to update old state and new augmented features separately and initialize the new covariance corresponding to new features elegantly. This procedure has also been mentioned in Section 2.2.2.Readers can refer to the work by Li and Mourikis20for details.The state correction can also be obtained after the process of aforementioned procedure.The expression of general state correction is presented as

where Δxoldis the correction for old filter state, and Δρnewis the correction for new augmented features state.

2.4. 1D IDP propagation

In this section, one of the main contributions of this paper is presented,which is an 1D IDP propagation equation for propagating covariance when the host frame changes.

For an augmented feature with tracking length longer than sliding window size,its host would drop out of the sliding window as time goes by. In this case, the latest camera frame will be selected as the new host. Meanwhile, the inverse depth under old host camera frame should be propagated to the new one, for both its value and covariance.

By using 3D IDP,an analytical propagation expression can be obtained naturally,since it preserves full degrees of freedom(DOFs). However for 1D IDP, approximations have to be made due to the loss of DOFs and imperfect measurement.VINS-MONO26also utilized 1D IDP in their implementation,and the parametrization details are similar to the proposed algorithm, both of which use observation in host frame and inverse depth to parametrize a feature point. However,VINS-MONO does not need to deal with the covariance propagation since it is an optimization-based solution.Engel et al.24proposed a method of propagating 1D IDP covariance in monocular dense visual odometry. However, it is deduced under the assumption of small rotation,and thus only translation in Z-axis of the camera frame is concerned,while an analytical 1D IDP translation expression considering overall state error is deduced in this paper, which will be presented in following paragraphs.

Also, the inverse depth in new host camera frame can be obtained by first propagating the feature position into the new host camera frame, and then calculating the reciprocal of the third element of this position, as shown below:

where

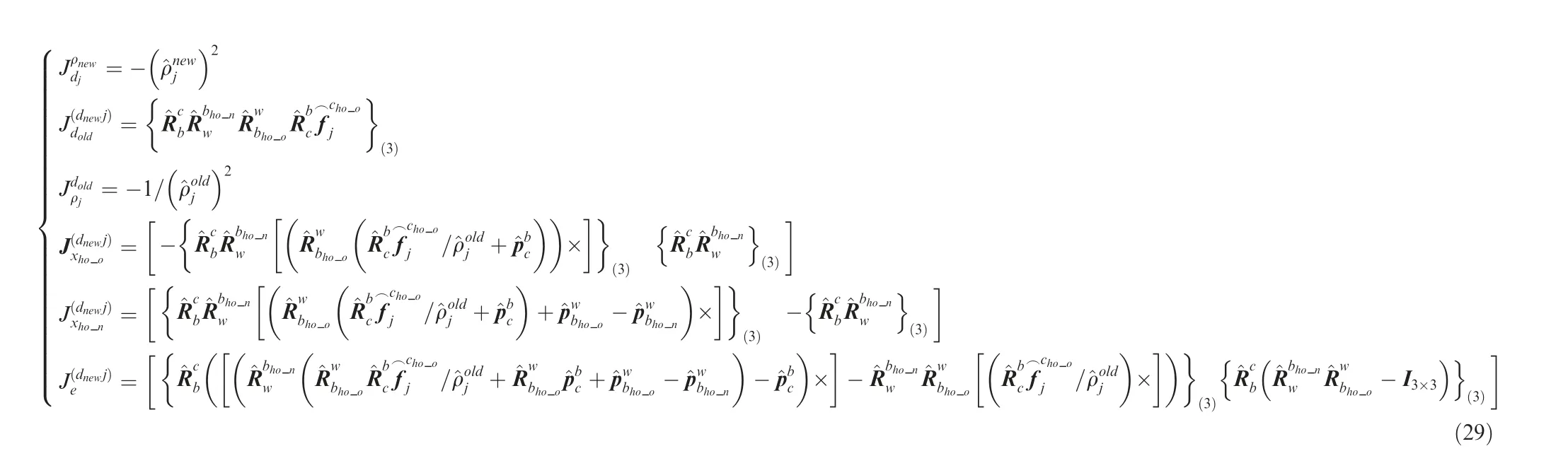
Similar to the 1D IDP initialization procedure proposed in Section 2.2.2,the observation of new host camera frame is corrected by the current feature position estimation, as shown in Fig. 4.

With Eq. (27), the covariance of the inverse depth in new host camera frame can be obtained, based on covariance of inverse depth in old host camera frame, IMU poses of old and new host and camera-IMU extrinsic parameters. This propagation would happen when the host frame of an augmented feature drops out of the sliding window and a new host is found.

Fig. 4 1D IDP translation by correcting observations.

3. Closed-form ZUPT

In this section, a closed-form ZUPT method is proposed,which is modeled as EKF measurement updates.ZUPT would happen once detecting static scene. The major contribution of applying ZUPT in hybrid VIO in this paper is that,by utilizing the structure of the filter(with a sliding window of poses in the state vector), three measurement residuals (zero-velocity,identical-position and identical-rotation) are constructed and the ZUPT is integrated into hybrid VIO as a natural measurement update.The static scene detection strategy and aforementioned three ZUPT measurement residuals are presented in detail. And the integration logic of static scene detection and ZUPT are also presented.

3.1. Static scene detection

ZUPT is often used in algorithms based on inertial sensors such as pedestrian navigation.In this category,the IMU measurement is often used to detect the static scene.30However,IMU measurement is noisy, in some degenerate motion such as constant speed moving,the IMU data might exhibit similar character as if it is static.This makes it tricky to tune the detection threshold. In VIOs, information from images could be used to detect the static scene.19Through statistical analysis,the pixel difference between matched points in static scene was found to be significantly small,which means that the static scene is very unique in the view of feature movement.So in the proposed implementation,static scene is detected by analyzing feature movement instead of using IMU data.

The main idea is very simple,which is to calculate the pixel difference of matched feature points in adjacent images, and use a threshold to judge if the scene is static.However,moving objects in a static scene might result in detection failure, since potential matched points on the moving objects contribute to large pixel differences. To deal with this situation, a simple experimental strategy was proposed: ten matched pairs with the largest pixel difference were deleted, and the largest pixel difference of the remaining pairs was compared with the threshold to judge if the camera is static.

This strategy works quite well in the experiments presented in this paper:few moving objects appeared in the static view would not result in detection failure,and slightly motion of the camera would not be judged as static thanks to the adopted significantly small threshold.However,this strategy might not work in every case.It could be imagined that this image-only detection strategy would fail if the camera is static in a place with large amounts of moving objects. A more completed method is needed to cope with the complex reality,such as combing the IMU data and feature movementto provide a morerobustdetection.Thiscould be included in the future work.

3.2. ZUPT measurement update

If the sensor’s carrier is static, its velocity is meant to be zero.Also, IMU poses corresponding to the adjacent static images should be the same.As the hybrid VIO keeps a sliding window of past IMU poses in the filter, this information can be used for measurement update upon detection of a static scene.

Three residuals will be introduced below. They are utilized for ZUPT measurement update when a static scene is detected by using information from the latest and second latest images.

3.2.1. Zero-velocity residual

Ideal measurement and its prediction for zero-velocity are listed as follows:

The equation above shows that the zero-velocity residual can be obtained by directly using current estimation of the IMU velocity,and this residual is a linear function about error state δ.

3.2.2. Identical-position residual

Identical-pose constraint is divided into two parts: identicalposition constraint and identical-rotation constraint. Ideal measurement and its prediction for identical-position constraint are listed as follows:

The equation above shows that the identical-position residual can be obtained by directly using the latest and the second latest IMU position estimation in the sliding window,and this residual is a linear function about error stateand.

3.2.3. Identical-rotation residual

Ideal measurement and its prediction for identical-rotation constraint are listed as follows:where ｛·｝（234）is an operator taking three coefficients of the imaginary part of a quaternion to form a 3D vector.The residual of identical-rotation constraint can be obtained by using the latest and the second latest IMU rotation in the sliding window,and this residual is a linear function about error stateand（n -1）.

3.3. ZUPT integration logic

In the proposed algorithm, static scene detection will take place once a new image is received. If the current image is detected as static, the INS and covariance propagation would still be conducted. But the conventional measurement update based on features would stop, since current image provide no further new information than last one. The residuals proposed in Section 3.2 will be used for a closed-form ZUPT.As a result, any quantity that would result in a biased INS propagation can be corrected by this update, such as ba, bgand qwb.

In the conventional routine, the oldest IMU pose will be deleted after conventional measurement update, only if the sliding window is full.However if ZUPT happened,the second latest IMU pose will be deleted, independent of whether the size of sliding window has reached maximum or not. This is because it provides redundant information to the latest one.

With these modifications added to the conventional routine, the overall flowchart of the proposed algorithm is depicted in Fig. 5.

Red blocks in Fig.5 also highlight other novelties proposed in this paper. The visual front-end for feature extraction and matching is based on a descriptor assisted sparse optical flow tracking, and filter state is initialized by detecting and using the static IMU measurements at the beginning of the sequences.19

4. Experiments

In this section, detailed experimental results and analyses are presented. The positioning precision and computational efficiency of the proposed algorithm are evaluated on both public dataset and real data while compared with baseline and the existing state-of-the-art algorithms. Also, to demonstrate the effectiveness of the proposed closed-form ZUPT method,experiments were conducted on real data with several deliberate stops, compared with algorithms without ZUPT. All the experiments were performed on an Ubuntu 16.04 virtual machine powered by MacBook Pro Mid 2015, assigned with two core and 8 GB RAM.

Fig. 5 Algorithm flowchart.

Furthermore,key setting of the implementation of the proposed algorithm is presented.The size of the sliding window is set to 20, and the maximum number of augmented features is set to 20. Also, FEJ was applied to correct the observability properties.7

4.1. Public datasets

The EuRoC dataset32was used to evaluate the performance of the proposed hybrid VIO. It provides eleven challenging sequences with synchronized images and IMU data collected by sensors on an UAV. The visual-inertial sensor in EuRoC used ADIS16488 MEMS (Micro-Electro-Mechanical System)IMU and MT9V034 global shutter camera. Data were collected in three different scenarios, including a machine hall and two Vicon rooms. In each scenario, sequences are classified as‘easy’,‘medium’and‘difficult’,representing complexity levels of the motion and light condition. High-precision ground truth is also provided making it to be a popular dataset for VIO algorithms evaluation.

The initialized parameters of the filter are given. The process noise intensity matrix φ is set as

The four 3×3 diagonal submatrices correspond to gyroscope white noise, accelerometer white noise, gyroscope bias random walk and accelerometer bias random walk respectively.

Notice that, to avoid symbol confusion by using R to represent two different meaning (rotation matrices and measurement noise covariance matrices), an unusual symbol M was used to represent measurement noise covariance matrices here.For each feature reprojection residual,its measurement covariance matrix is set as

It means that the standard deviation of reprojection measurement residual is set as 1 pixel, and it would be divided by the focal length f to be transformed into a quantity under the unified camera coordinate.

Fig. 6 shows the results of the proposed algorithm and algorithms listed in Table 2 on several sequences of EuRoC.Estimated trajectories and the corresponding ground truth are plotted.

4.1.1. Analysis of positioning precision

Table 2 lists the Root-Mean-Square Errors (RMSEs) of the estimated trajectories, resulted from the proposed algorithm and several state-of-the-art monocular VIOs.

To make a fair comparison between pure VIOs, the loopclosure function was turned off in VINS-MONO. Each algorithm was run 50 times on every sequence and the mean RMSEs are calculated and listed in the table. The best results are highlighted in bold.

As it can be seen from the results, the proposed algorithm generally performs the best among all the listed algorithms.On comparison with VINS-MONO,26which is a popular open-sourced optimization-based VIO solution, the proposed algorithm performs better in 9 out of 11 sequences. Also, the proposed algorithm completely outperforms R-VIO,29which is also a member of MSCKF family utilizing the robocentric formulation to avoid the observability mismatch.These experiments demonstrate the competitive performance of the proposed solution in positioning precision compared to the state-of-the-art algorithms in terms of positioning precision.

By comparing with the baseline MSCKF that the proposed algorithm was built on, precision improved especially on relatively large scenery sequences (MH_01-MH_05), while small improvements are acquired in Vicon rooms. This is due to the relatively short tracking lengths of features in Vicon rooms. The tracking lengths of features in each scenario are analyzed.In machine hall sequences,some augmented features would be tracked for up to more than 40 seconds (nearly 800 frames under 20 Hz sampling rate), compared to the augmented features in Vicon rooms which were tracked for 15 seconds at most. The phenomenon of the relatively large improvements in machine hall sequences, from another point of view, demonstrates the effectiveness of utilizing complete constraints of features with relatively long tracking length.

A hybrid VIO using 3D IDP was also implemented as a baseline algorithm. The variance of RMSEs are very large in every 50 runs for each sequence, resulting in relatively downgraded averaging results in Table 2.By using 3D IDP,the state dimension sometimes becomes very large, which increases the computation demand. Also, since the constraints in XYplane of a camera frame are stronger than in Z-axis, the convergence rates of XY-axes are faster than that of Z-axis for a 3D IDP feature. This convergence issue sometimes results in numerical instability, leading to bad performance.

4.1.2. Analysis of computational efficiency

The computational efficiency of the aforementioned algorithms is also analyzed. The average process time of the filter or optimization back-end for algorithms in Table 2 is listed in Table 3. The loop-closure of VINS-MONO is turned off in this experiment as well.

As can be seen in Table 3, MSCKF and R-VIO have the most efficient back-ends, since they are filtering-based solutions only utilizing MSCKF features for measurement update.The optimization-based back-end of VINS-MONO takes nearly 50 ms for computation after receiving each image which is mainly due to the iterative mechanism of nonlinear optimization.

The proposed algorithm takes on average 8.16 ms for measurement update for every image. Compared to MSCKF, the extra computations are mainly due to larger state dimension,and these computations render into higher precision in estimation results. By comparing to VINS-MONO, as can be concluded from both Tables 2 and 3, the proposed method provided better positioning precision while demanding far less computation.

By comparing to the baseline using 3D IDP, the proposed 1D IDP solution requires about 2 ms less for every image.Notice that, the maximum number of augmented features is set to 20 in experiments. As the computation complexity of a l-dimensional EKF is O(l2),the superiority in computation of the proposed 1D IDP will be more significant if the number of augmented features increases, compared to the 3D IDP solution.

Fig. 6 Estimation results of proposed algorithm on EuRoC dataset.

Table 2 RMSEs of estimated trajectories (m).

Table 3 Back-end process time for each image.

4.2. Real data

Two indoor handheld datasets were collected for real data experiments. The MYNT EYE Depth stereo camera (D1000-IR-120/Color) was used for data collection. The sensor suite consists of a BMI088 MEMS IMU and two AR0135 global shutter cameras. It outputs hardware synchronized 20 Hz global-shutter images and 200 Hz IMU measurements. As the algorithms used in experiment are monocular VIOs, only the images of left eye were used. The datasets were collected by people hand holding the sensor suite and walking in normal speed(no more than 2 m/s).Since no ground truth is available,the camera was made to return to the initial point at the end in collected datasets, making it possible to evaluate the performance by computing loop error.

The initialized parameters of the filter are the same as in experiments on EuRoC, except for the process noise intensity matrix, which is shown as

The difference between Eq. (38) and Eq. (40) is due to the different IMU properties in EuRoC dataset and the real data.

4.2.1. Data 1: Loop with down and up stairs

A sequence was collected, which contains movements of descending and ascending stairs, and some typical image of the scene is shown in Fig.7(a).This sequence occasionally suffers from severe bad light condition and low texture,which are challenging scenerios for VIOs. Features close to the vanish point will be continuously tracked during the movement in the straight corridors, which can be utilized by the proposed hybrid VIO to improve the positioning precision.

The estimation results of algorithms listed in Table 2 are aligned using 3D similarity transformation, and plotted in Fig. 8(b). The distinct loop errors of 3D IDP solution and R-VIO can be observed. However, the proposed algorithm,MSCKF and VINS-MONO gave similar estimation results.Estimated trajectories of these three algorithms are plotted in Fig. 7(c). Their absolute and relative loop error are listed in Table 4.

Fig. 7 Typical images and estimation results of Data 1.

Table 4 Absolute and relative loop error of estimations of Data 1.

On one hand, as shown in Table 4, the proposed 1D IDP solution has the best performance among all the listed algorithms. Improvement is also gained in comparison with baseline MSCKF, due to the superiority of the proposed algorithm which also utilizes the complete constraints of features with very long tracking length. On the other hand, the 3D IDP implementation suffers from the numerical instability and results in downgraded performance.

4.2.2. Data 2: Circle around corridor

Another dataset was collected, where the camera circled around a rectangular corridor for four rounds. Estimated trajectories are plotted in Fig. 8.

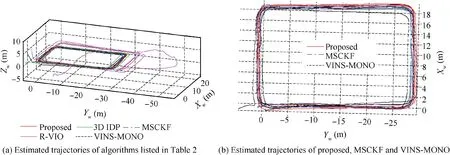
Fig. 8 Estimation results of Data 2.

Table 5 Absolute and relative loop error of estimations of Data 2.

As shown in Fig.8(a),the estimation of 3D IDP implementation is inconsistent, and the estimation of R-VIO suffers from huge deviation at the beginning of the sequence(R-VIO would take time to converge as it does not have an explicit initialization procedure). But the proposed algorithm,MSCKF and VINS-MONO relatively perform better, and the results of these three algorithms are plotted in Fig. 8(b).VINS-MONO encountered with large drift after the camera stopped at the end,since no ZUPT was applied in their implementation.To make a fair comparison,this drift was removed when calculating the loop error, and the absolute and relative loop error of the proposed algorithm, MSCKF and VINSMONO are listed in Table 5.

From Table 5, we can see that the proposed algorithm has better performance than others. Notice that the loop-closure function in VINS-MONO is prohibited. With its full ability,VINS-MONO can achieve very high precision by utilizing loop constraints between repetitive same scenarios in this sequence.

4.3. ZUPT evaluation

The third real dataset was collected with several deliberate stops and a loop end, to testify the effectiveness of the proposed ZUPT methods. Estimation results of the proposed 1D IDP implementation with and without ZUPT are plotted in Fig. 9. The result of algorithm with ZUPT can nearly close the loop, while the result of algorithm without ZUPT suffers from unnatural jumping update at the stop points, resulting in downgraded performance. When not applying static scene detection and ZUPT, biased estimation of IMU biases or orientation would result in biased propagation. When using a low-cost IMU, as the BMI088 used in this experiment, the error of biased propagation is sometimes unneglectable. The mechanism of MSCKF is using lost features for measurement update, and apparently little features would be lost when the camera is static, and meanwhile in the proposed hybrid VIO,the number of augmented features is limited (there will be no augmented feature if no feature is tracked for very long time or successfully initialized).So sometimes there will be no measurement update or only weak measurement update with little features when the camera is static, and the estimation would somehow drift by only/mostly applying biased propagation.When the camera started to move again, the upcoming effective measurement then resulted in sudden changes in trajectory estimation of algorithm without ZUPT, as is visible in Fig. 9.

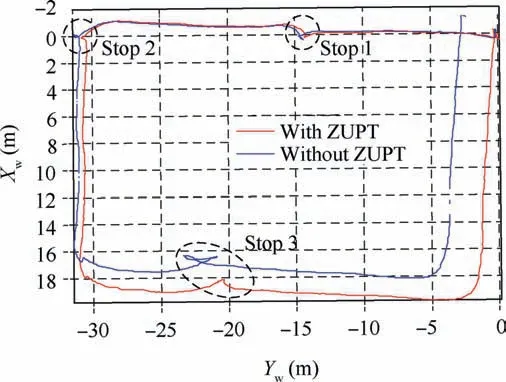
Fig. 9 Estimation results of the proposed algorithm with and without ZUPT.

For the ideal static constraint, the ZUPT measurement noise covariance Mzuptshould be zero. However, considering potential false detection that identifies very slow motion as static scene,a Mzuptwith small quantity is utilized to improve the fault detection tolerance. It is shown as

Three submatrices are corresponding to zero velocity,identical position and identical rotation respectively.

VINS-MONO is also tested on this dataset. However, it outputs trajectory with huge drift after the first stop.The constraints of the proposed ZUPT in Section 3.2 have the potential to be used to improve the performance of VINS-MONO,or other VIO solutions.

4.4. Discussion

As shown in the experimental results, the proposed algorithm improves both the positioning precision and computational efficiency compared to the baseline 3D IDP solution. This is achieved by reducing the state dimension and improving the numerical robustness through applying 1D IDP for augmented features. Also, the performance of the proposed algorithm is comparable to the state-of-the-art optimization-based VIO in terms of precision, while demanding far less in computation cost.By formulating the ZUPT as a measurement update procedure,the proposed algorithm is able to correct the state estimation resulting in biased propagation and avoid the jumping in trajectory.

More works can be done, which have the potential to further improve the performance of the proposed algorithm.The selection of augmented features is relatively rough in the current implementation: the top N longest tracking features are selected as the augmented features. But in certain scenarios, these features might be centered in a narrow space on the image plane. For example, the features with long tracking length might be centered on objects with more texture than others. These features have similar directions, and thus the information that they provide is partially redundant. With a more sophisticated augmented features selection strategy,such as considering the spatial distribution along with the tracking length, the information utilization might be improved, resulting in better performance for the algorithm. Also, as mentioned in Section 3.1, a static scene detection method considering both IMU data and information from image might improve the detection robustness in a complicated scenario.

5. Conclusions

The following is a list of main conclusions that can be drawn.

(1) A novel monocular hybrid VIO using 1D IDP for feature states is proposed. The computational efficiency and positioning precision are both highly improved compared to the baseline algorithm using 3D IDP.

(2) A method is proposed to deal with the 1D IDP propagation whenever the host frame drops out of the sliding window. A 1D IDP error propagation equation is deduced, which considers errors of overall state.

(3) A closed-form ZUPT is proposed to cope with the static scene in vehicle movement.Three constraints are considered and used to construct measurement residuals to naturally conduct the ZUPT in an EKF framework.And a static scene detection method based on features movement analysis is introduced.

(4) Online temporal and camera-IMU extrinsic parameters calibration are introduced to further improve the estimator’s performance. FEJ is utilized to correct observability property and improve estimator consistency.

(5) Experiments on challenging public datasets and real data demonstrate the effectiveness of the proposed methods.The proposed VIO demands far less computation while providing higher positioning precision compared to the state-of-the-art algorithms.

(6) Further experiments are conducted to demonstrate the effectiveness of the proposed ZUPT method. The constraints in the proposed ZUPT method have the potential to be used for improving the performance of other VIOs.

Future works include exploration of augmented features selection strategy and robust static scene detection method.Also,other special motion constraints,such as planar motion,can be introduced into the proposed algorithm to improve the performance in certain scenarios.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors are grateful to Qu Xingwei and Guo Rongwei for discussion. This study was supported by the National Key Research and Development Program of China (Nos.2016YFB0502004, 2017YFC0821102).