A dynamic modeling approach for nonlinear vibration analysis of the L-type pipeline system with clamps

Qingdong CHAI, Jin ZENG, Hui MA,b,*, Kun LI, Qingki HAN

a School of Mechanical Engineering and Automation, Northeastern University, Shenyang 110819, China

b Key Laboratory of Vibration and Control of Aero-Propulsion Systems Ministry of Education of China, Northeastern University, Shenyang 110819, China

KEYWORDS Clamp;Dynamic modeling;Experimental test;Finite element;Nonlinear vibration;Pipeline

Abstract There exists a lot of research on the nonlinear vibration of the pipeline system with different boundary conditions.To the best of our knowledge,little research on the actual constraint of the clamp has been performed. In this paper, according to hysteresis loops of the clamp obtained from experimental test, the simplified bilinear stiffness and damping model is proposed. Then the Finite Element (FE)model of L-type pipeline system with clamps is established using Timoshenko beam theory in combination with aforementioned stiffness-damping model. Both hammering and shaker tests verify the FE model via the comparisons of natural frequencies and vibration responses.The results show that the maximum errors of natural frequencies and vibration responses are about 8.31% and 17.6%, respectively. The proposed model can simulate the dynamic characteristics of the L-type pipeline system with clamps well, which is helpful to provide some guidance for the early design stage of pipeline in aero-engine.

1. Introduction

Pipeline system is widely applied in aero-engine, and it is usually fixed on the casing by clamps (see Fig. 1). The external pipeline failure caused by vibration will affect the reliability of the aero-engine, so it gradually becomes a research hotspot.1,2

Clamps play an important role in vibration characteristics of pipeline systems. Some scholars have conducted researches on mechanical properties of clamps. Yin and Chen3derived the clamp stiffness by Finite Element (FE) method and the simulated stiffness was verified by experiment. Li et al.4used the tensile testing machine to measure the clamp stiffness and the influence of the temperature on it was studied.Ulanov and Bezborodov5-7calculated the support stiffness and energy dissipation coefficient of the clamp via the hysteresis loops under the static load,and simplified the clamp as a set of linear springs and angular springs.Gao and Sun8obtained the hoop stiffness and damping by inverse method combined hammer test and analyzed the effect of the preload. Considering the asymmetry of the clamp structure, piecewise linear stiffness of the flexible clamp was adopted in Ref.9.In Ref.10,the supporting components were discretized into several springs and the influence of support parameters on natural frequencies of the pipeline was analyzed.

Fig. 1 Pipeline system with clamps in aero-engine.

Prediction of the dynamic characteristics of pipeline systems is of great significant. In recent decades, researches on dynamic modeling of pipeline systems with different boundary conditions have been extensively performed by many scholars.Some researches mainly focused on the dynamics of pipes with classical boundaries such as clamped-clamped, clampedpinned,and cantilevered pipes.11-14In addition,many scholars devoted to vibration analysis of straight pipes with end supports and intermediate supports.15-21Dynamic behavior of a pipe subjected to a moving sprung mass was investigated in Ref.22. There are also many researches considering the viscoelastic supports and elastic foundations.23-25In Refs.26-28,vibration characteristics of multi-span fluid-conveying pipeline were investigated. Liang et al.29studied the dynamic behavior of a fluid-conveying pipe subjected to harmonic load. Zhang et al.30investigated the dynamical modeling of cantilevered pipe conveying pulsating fluid with harmonic external force.Ding et al.31established the nonlinear dynamic model of the pipeline system with nonlinear isolators. Dynamic modeling and vibration analysis of the aerospace pipeline system with hoops were carried out in Refs.32,33. Liang et al.34analyzed the transverse free vibration and stability of spinning pipelines.

In addition to straight fluid-conveying pipes,some scholars have conducted researches focus on complex pipeline system.Wiggert et al.35discussed the effect of elbow restraint on pressure transients and the model established could accurately predict the experimental results. Based on the transfer matrix method,Lesmez et al.36conducted modal analysis of vibration in liquid-filled piping systems, including single bend piping system and U-bend piping system.Heinsbroek and Tijsseling37analyzed the influence of support rigidity on water hammer pressures and pipe stresses of liquid-filled pipe systems.Kwong and Edge38presented a technique combining transfer matrix methods with genetic algorithms which could reduce noise and vibration in hydraulic systems by optimizing pipe clamps locations. Tang et al.39established the parametric FE model of the hydraulic pipelines and performed an optimization for the location of the hoops which could effectively decrease overall stress and strain of the system. Aiming to the selected pipeline system in CAESAR II, Zahid et al.40developed a methodology for flexibility analysis which can be adjusted for the analysis of various pipeline systems. To further reduce the computational cost for design optimization of pipe systems, numerical surrogate models based on the Kriging and others were investigated in Refs.41,42. Compared with the traditional optimization method of hydraulic pipeline system, the optimization method based on sensitivity analysis proposed in Ref.43is superior in efficiency and results. Zhang et al.44adopted the non-probabilistic sensitivity analysis to screen out the hoops which were insensitive and the position coordinates of the remaining constraint hoops were further optimized. Zhou et al.45studied reliability and global sensitivity analysis in an uncertainty scheme which guided the probabilistic anti-resonance design of aeronautical hydraulic pipelines.Xu et al.46analyzed the vibration response of piping systems with complex constraints, boundary conditions and spatial configurations and the methods presented were proved by experiments.

There are also many experimental researches about pipeline system. In Refs.47-50, traditional test instruments including accelerometer and strain gauge were adopted. And the emerging FBG sensor has gradually been used in many researches.51-53Ouyang et al.47established a two-dimensional model to study the stress condition of the pipeline which was verified by experiment.In their later work,the transfer matrix method was applied to determine the modal characteristics of the space pipe and the experiment results illustrated the correctness of the developed model.48Qu et al.49studied the influence of transverse support stiffness on dynamic characteristics of pipeline under base excitation, the experimental results showed a good agreement with the simulated results.In Ref.32,the simulated natural frequencies in FRFs were also validated by experiment test. Wei et al.50studied the flexural vibration transfer properties of high-pressure periodic pipe combined with experiments. The natural frequencies captured by Fiber Bragg Grating (FBG) sensors were obtained in Ref.51, which was consistent with the simulation. And they pointed out that the FGB sensors could resist electromagnetic interference.Wang et al.52proposed a new method to detect clamp looseness based on the Strain Mode Shape Differences (SMSD)and FBG sensing technology. Huang et al.53described multiparameter measuring principle of the FBG and the framework of the proposed system.

According to the above literature reviews, most researches focus on theoretical study of dynamic characteristics of straight pipes, and less attention is paid on L-type pipeline system with clamps. Meanwhile, corresponding experimental verifications are also rare. Aiming to the existing deficiencies in the literatures, a series of modeling approaches including the determination of clamp stiffness and damping, the equivalence of clamp stiffness and damping and the establishment of mathematical model are applied to evaluate the dynamic characteristics of the L-type pipeline system with clamps quantitatively. More importantly, the dynamic characteristics of the pipeline system with clamps are verified by some experimental tests.

This paper is arranged as follows: In Section 2, the formulation and modeling of the clamp and L-type pipeline system with clamps is derived elaborately. Then the dynamic model of the L-type pipeline system with clamps is verified via hammering and shaker tests in Section 3.Finally,some conclusions are summarized in Section 4.

2. Formulation and modeling

L-type pipeline supported by clamps(see Fig.2)is taken as the research object in this paper. Specifically speaking, an equivalent modeling method of clamp stiffness and damping is proposed. The FE model of the pipeline is discretized by the Timoshenko beam element.54-57Then the dynamic model of the L-type pipeline system with clamps is established by coupling the FE model of the L-type pipeline with the equivalent model of the clamps. It should be noted that the pipeline is in xOy plane (see Fig. 2(a)).

2.1. Stiffness-damping determination of the clamp

2.1.1. Discrete model of the clamp

The discrete model of the clamp considering the effect of the clamp width is proposed in this section. In Fig. 3, the constraint of the clamp in the direction of the bolt constraint is discretized, which will restrict the movement out of the xOy plane of the pipeline.It should be noted that the discrete model of the clamp in the horizontal direction (in xOy plane) is similar to the model in Fig. 3, which will not be shown in this paper. To be specific, the clamp with the width of 14 mm is divided into eight springs and dampers along the axial direction, including two linear springs Kz/2, two angular springs Kθy/2, two linear dampers Cz/2 and two angular dampers Cθy/2. The distance between the linear or angular springs and dampers is the width of the clamp, and the stiffness and damping of each spring and damper is half of the measured stiffness and damping in that direction. Due to the tightening moment of the clamp is 7 N·m, the friction between the pipeline and the clamp is large enough to prevent the pipeline from axial and torsional motion. Therefore, the axial stiffness Kxand torsional stiffness Kθxof the nodes corresponding to the middle position of the clamps are set to be infinite, here,Kx=1×1011N/m, Kθx=1×1011N·m/rad.

2.1.2. Determination of the clamp stiffness

The clamp stiffness is obtained by the relationship between loading force and deformation.

where ΔFy,ΔFzrepresent the variation of the loading force in y and z directions; ΔMy,ΔMzrepresent the variation of the torque in the θyand θzdirections; Δy, Δz represent the variation of the displacement in the y and z directions; Δθy, Δθzrepresent the variation of the angular displacement in θyand θzdirections.

The self-designed test rig is shown in Fig.4,which is used to measure the clamp stiffness.During the test process,the tightening torque of the clamp is set as 7 N·m. The test rig for calibrating linear stiffness of the clamp is shown in Fig. 4(a). To be specific,the process of loading and unloading is carried out through screw thread parts. And the displacement of loading and unloading is controlled internally by the support spring.Furthermore, in order to load precisely and avoid clearance during the process of loading and unloading, the forward and backward distance of the handwheel is amplified by the support spring. The displacement is measured by a dial gauge during the test.

Fig. 2 Test rig of L-type pipeline system with clamps.

Fig. 3 Discrete model of clamp in z direction.

Fig. 4 Test rig of clamp stiffness.

Fig. 5 Experimental clamps.

As for the test rig of angular stiffness, the loading method of worm gearing transmission is adopted to apply torque precisely (see Fig. 4(b)). The resolution of the angle sensor is 0.01°, which could meet the requirement of the test fully.

In order to consider the dispersion of the clamp stiffness,four clamps are chosen randomly from plenty of clamps and the stiffness of each clamp was tested twice. And the selected clamps for test are shown in Fig. 5.

A test case of the linear stiffness and angular stiffness of the clamps is shown in Fig. 6, which includes hysteresis loops and fitting stiffness.The rest test data will not be shown here owing to space constraints.A complete test sequence in the process of calibration of the clamp stiffness includes forward loading,forward unloading, reverse loading and reverse unloading. And the direction of loading and unloading is shown in Fig. 6(a),where the ‘O’ represent the origin of the test. Because the actual structure of the clamp is asymmetric in the transverse direction, the support stiffness of the clamp in the y and z direction is assumed to be bilinear. The measured hysteresis loops of the clamp and the bilinear stiffness fitted by least square method are shown in Figs.6(a)and(b). To be specific,the upward stiffness of the clamp is obtained by fitting the process of forward loading and forward unloading. And the downward stiffness of the clamp is obtained by fitting the process of reverse loading and reverse unloading. On account of the angular stiffness in θyand θzdirections of the clamp are symmetric (see Figs. 6(c) and (d)), they are obtained by fitting the whole hysteresis loops through the method of linear fitting.And the final equivalent stiffness of the clamps is acquired by averaging all the measured fitting stiffness of the four clamps.Based on the above analysis and calculation,the bilinear transverse stiffness and angular stiffness of the clamp obtained from the experiments are shown in Table 1. It should be noted that static characteristics are supposed to be equal with dynamic characteristics of the clamp in this paper.5

Fig. 6 Measured hysteresis loops and fitting stiffness in different directions.

Table 1 Clamp stiffness in different directions.

2.1.3. Determination of the clamp damping

Hysteresis loop is an important way to express the characteristics of energy dissipation of the system. Considering the influence of material nonlinearity, the clamp damping is estimated by measured hysteresis loops. The Equivalent Viscous Damping Coefficient(EVDC)is determined by analyzing the hysteresis loops of the clamp. It should be noted that the detailed derivational process of the EVDC can be found in Ref. 58,which can be expressed as

where K is the measured stiffness of corresponding direction;η=0.2 is the damping loss factor59; ferepresents excitation frequency. The EVDCs in different directions is shown in Table 2.

2.2. FE model of the pipeline

According to the basic idea of FE method, the pipeline is discretized by the Timoshenko beam element. The establishment of FE model of the pipeline is composed of three parts including derivation of the partial differential equations of the Timoshenko beam element, acquisition of element matrices of the Timoshenko beam and element matrices assembling.

2.2.1.The partial differential equations of the Timoshenko beam element

Considering the axial, torsional, in-plane bending and out of plane bending deformation of the pipe, it is discretized by Timoshenko beam element which is shown in Fig. 7. Oxyz is the local coordinate system; u, v, w, and θ， φ， φ denote displacements in axial and transverse directions and angular displacements in rotation directions, and subscripts m and n denote nodes m and n, respectively.

Fig. 7 Timoshenko beam element.

The general displacement vector of the beam element uein the local coordinate system is given as follows:

where ρ, lkand A are the density, the kth element length and the cross-sectional area, respectively; Ix, Iyand Izthe area moments of inertia of cross-section about Ox, Oy and Oz,respectively;u,v and w are the linear displacements of centroid’O’ of arbitrary beam cross-section along positive x, y and z axes,respectively;θ,φ and φ are adopted to describe the angular displacements of an arbitrary rigid beam cross-section in Oxyz. The over-dot in Eq. (4) represents differentiation with respect to time.

The potential energy U of the kth Timoshenko element is shown as follows:

where E and G are the Young’s modulus and the shear modulus,respectively;J is the torsional moment of inertia;κyand κzare the shear coefficients in the y and z directions,respectively.

Table 2 EVDCs in different directions.

2.2.2. Element matrices of the Timoshenko beam

In order to solve Eqs.(6)-(11),the displacement field functions in the x,y,z,θx,θyand θzdirections are assumed and here the vectors of shape functions in different directions are shown as follows

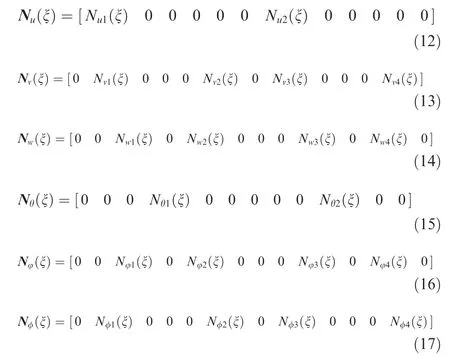
In Eqs. (12)-(17), the expressions of the shape functions Nmi(ξ) (m=u, θ; i=1, 2), Nni(ξ) (n=v, w, φ, φ; i=1, 2,3, 4) can refer to Ref.60.

Fig. 8 Relationship between local coordinate system and global coordinate system.

Substituting Eqs. (12)-(17) into Eqs. (6)-(11), the element stiffness and mass matrices in the local coordinate can be expressed as

2.2.3. Element matrices assembling

For a hybrid pipe composed of curved segment and straight segment, transformation from local to global coordinate system must be operated before assembling the element mass matrix and element stiffness matrix. The matrix transformation formulas of the kth element are shown as follows:

where T is the transformation matrix from global coordinate system OXYZ to local coordinate system Oxyz; ukis the displacement vector of the kth element in global coordinate system; λk(see Fig. 8) is the angle of X axis in global coordinate system relative to the x axis in local coordinate system of the kth element.

To be specific,the derivation of cos λkand sin λkin Eq.(20)can be written as follows:l

where N is the number of beam elements.

2.3. FE model of L-type pipeline system with clamps

The material and geometric parameters of the L-type pipeline(see Fig. 9(a)) are listed in Table 3.

Fig. 9 Model of L-type pipeline system with clamps.

Table 3 Material and geometric parameters of L-type pipeline.

The three-dimensional CAD model of the L-type pipeline is shown in Fig. 9(a). The dynamic model of the L-type pipeline system with clamps along the Z direction is established by coupling the FE model of the pipe with the discrete model of the clamps (see Fig. 9(b)). Considering the effects of the clamp width and computational efficiency, the pipe is divided into seven sections. And the element length from pipe Section 1(PS1)to pipe Section 7(PS7)is not quite the same.Specifically speaking, the pipe section with the clamp is divided finely to obtain appropriate results. The Number of the Element (NE)and the element length of each pipe section are shown elaborately in Table 4, which illustrate the location of each node.It should be noted that pipe Section 4 (PS4) is considered to be the synthesis of a series of short straight beam elements.The equivalent springs and dampers of clamp 1 are located at node 25 and node 39, and the equivalent springs and dampers of clamp 2 are located at node 111 and node 125 respectively.

The equations of motion of the L-type pipeline system with clamps can be written as follows:

According to the orthogonality of modes of vibration, Eq.(25) can be written as62,63

Table 4 Element information of different pipe sections.

Fig. 10 Structure of entire assembled stiffness matrix.

where a represents the excitation amplitude of acceleration; ferepresents excitation frequency;t represents excitation time;G represents displacement indicator vector of the pipeline which is composed of‘0’and‘1’.And in the direction of Z,the value in vector G is ‘1’, otherwise it is zero. And the acceleration response of the L-type pipeline system with clamps is ¨u. Then the relative acceleration between the base and the pipeline is¨ur.The relationship among the above three can be expressed in the following form

The equation of motion for solving the dynamic responses of the L-type pipeline system with clamps can be written as follows:

Substituting Eq. (30) into Eq. (31), the equation of motion of the pipeline system with clamps can be expressed as

Eq. (32) indicates that the response of the L-type pipeline system with clamps under base excitation is caused by inertial force applied on the pipeline which is converted by ¨ug. It should be noted that the inertial force is equivalent to the distributed force which is applied on each node of the pipe.

3. Model verification

3.1. Model verification based on natural characteristics

The hammering test is shown in Fig.1(a),where the tightening torque of the clamps is still set as 7 N·m. Furthermore, an impact hammer (PCB086C01) and unidirectional accelerometer (CA-YD-125, mass 1.5 g) are adopted. It should be noted that the mass of the sensor can’t be ignored on account of the mass of the pipeline is only 68 g, and the unidirectional accelerometer is modeled as a lumped mass point (1.5 g). All the parameters of the L-type pipeline system with clamps in the experiment are same as the FE model in Section 2.3.Then the FE model is verified by comparing the natural frequencies and mode shapes of simulation with experiment.

It should be noted that the natural frequencies of bilinear stiffness model can be obtained by64-67

Fig. 11 Comparison of measured and simulated FRFs.

Table 5 Comparison of simulated and measured natural frequencies.

where fbrepresents the natural frequency of the system;fdsrepresents the natural frequency obtained by downward stiffness;fusrepresents the natural frequency obtained by upward stiffness.

The measured and simulated FRFs are shown in Fig.11.It should be noted that node 81 is the excitation point (p=81)and node 96 is the measurement point (q=96) of sensor in Fig. 11(a); node 1 is the excitation point (p=1) and node 66 is the measurement point (q=66) of sensor in Fig. 11(b).The number of selected modal ‘n’ in Eq. (28) is set as 10. In Fig. 11, the trend of the FRFs of acceleration between the experiment and simulation are in good agreement. Rayleightype damping was adopted in this section which is difficult to reflect the actual modal damping of the system, so there is some error at the peaks of the FRFs.The simulated and measured natural frequencies of the L-type pipeline system with clamps are listed in Table 5. The maximum error of the simulated natural frequency is 8.31% which appears in the sixth order.

The first six-order simulated and measured mode shapes are shown in Fig. 12. In the figure, the general trend of simulated and measured mode shapes is consistent with each other. It should be noted that the experimental mode shapes are obtained by knocking the nodes in and out of XOY plane respectively. On account of random error in measurement,there exist some differences between experimental and simulated results.

3.2. Model verification based on vibration responses

3.2.1. Constant frequency test

The L-type pipeline system with clamps in aero-engine is always subjected to periodic excitation, and structural resonance will happen when the excitation frequency close to the natural frequency of the system. The pipeline in aero-engine is always fixed on the casing by clamps. When the casing moves, the L-type pipeline system with clamps will move with it.As the external excitation of the pipe acts on the lateral,the Z-axial elastic supports play a major role in the system (see Fig. 9(b)). The acceleration responses of node 66 will be extracted.Corresponding test rig of the L-type pipeline system with clamps is shown in Fig. 1(b). The pipeline is fixed on the shaker by clamps and fixtures,and the shaker is used to simulate the base excitation. The experimental data is collected via the LMS front controller of data acquisition.According to the tested response curve on the casing of a certain type of engine under a specific working condition,the harmonic frequency of 206 Hz possesses the highest excitation amplitude (2.6 g).Therefore, the external excitation frequency is 206 Hz and the excitation amplitude of acceleration is set as 1 g, 2 g and 3 g, respectively.

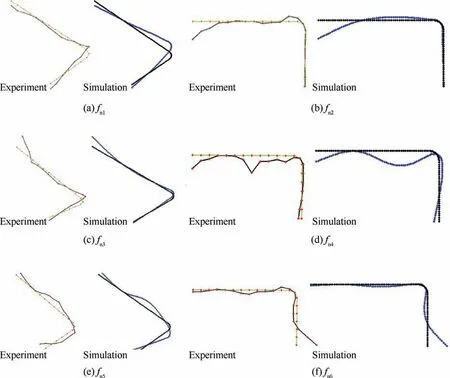
Fig. 12 Mode shapes.

Fig. 13 Comparison of measured and simulated responses with different excitation amplitudes.

Fig. 14 Spectrum cascades obtained from frequency-sweep test.

The simulated and measured steady responses are compared in the first row of Fig. 13, one can observe that the results of experiment are in good agreement with those of simulation under different excitation amplitudes. The maximum error of simulation is no more than 17.6%. Multi-harmonic frequency components could be found in the spectrums (see the second row in Fig. 13). Excluding the amplitude of fe,the amplitudes of 2feand 4feare higher than that of 3fe,which is mainly because 2feand 4feare close to fn3and fn5(see Table 5)of the system thus leading to amplitude amplification.

3.2.2. Frequency-sweep test

Fig. 15 Spectrum cascades obtained from frequency-sweep test around fn1.

In terms of the frequency-sweep test, the first-, third-, fifth-,and seventh- order natural frequencies are 241.5 Hz,412.5 Hz, 785.0 Hz and 1210.0 Hz, respectively (see Fig. 14),which is also in accordance with those obtained from the proposed FE model and the hammering test(see Table 5).In order to illustrate nonlinear characteristics of the system caused by the varying stiffness of the clamps, the frequency-sweep zone around fn1(see Fig. 14(a)) is taken as an example and corresponding results (take the logarithm of the amplitude)obtained from the numerical model and the experimental test are shown in Fig. 15. The multi-harmonic frequencies fe, 2fe,3fe, 4fe, 5feand the first-order natural frequency fn1exist in both the numerical and experimental models,which illustrates the efficiency of the proposed FE model to some extent.However,it has to be admitted that there also exist some minor differences in the spectrum cascades between the proposed model and the experiment such as the occurrence of the non-integer harmonic frequencies (see Fig. 15(b)). This is mainly because it is difficult to take all the actual testing conditions into the proposed model. As a whole, the results obtained from the proposed model are satisfactory.

4. Conclusions

(1) The stiffness and damping of the clamp are obtained based on the self-designed test rig.Considering the influence of the width of the clamp,the dynamic model of the L-type pipeline system with clamps adopting the finite element (FE) method is established. The FE model of the system is verified by the hammering test and the maximum error of the natural frequency is about 8.31%.

(2) The bilinear characteristic of the clamp stiffness along the direction of bolt constraint is proved by the shaker test. Multi-harmonic frequency components could be found in the system responses under harmonic base excitation. And the maximum error of time-domain response is about 17.6%, which further verifies the proposed model.

It should be noted that the dynamic model of the L-type pipeline system with clamps is established on the basis of determination of the clamp stiffness and damping. The effects of fluids on the dynamic characteristics of the L-type pipeline system with clamps are not considered,which will be studied elaborately in the following studies.

Acknowledgements

This project is supported by National Natural Science Foundation of China (No. 11772089), Fundamental Research Funds for the Central Universities (Nos. N170308028,N170306004 and N180708009), Program for the Innovative Talents of Higher Learning Institutions of Liaoning(LR2017035).