港口高耸烟囱风荷载的风洞试验研究及中美规范对比

高 科

(河北港口集团港口工程公司，秦皇岛 066000)

高耸烟囱结构属于风敏感结构，其顺风向及横风向等效静风荷载的确定是结构设计的关键环节之一[1-2]。港口风灾频发，设计风速较大，因此港区风敏感结构的抗风安全尤为重要。复杂环境干扰下的高耸烟囱设计风荷载取值往往需要通过风洞试验确定[3-5]。不同于高层建筑结构[6]，烟囱结构风洞试验结果与国际相关规范的对比研究较少。本文以某港口电厂275 m混凝土烟囱为例，设计风速为80 m/s(50 a一遇，开阔地貌，10 m高，3 s阵风风速)，通过风洞试验及风振响应分析确定了该烟囱的等效静风荷载，并与中国规范《建筑结构荷载规范》(GB50009-2012)[7]、《烟囱设计规范》(GB50051-2013)[8]、美国规范MinimumDesignLoadsforBuildingsandOtherStructuresASCE7-16[9]及CodeRequirementsforReinforcedConcreteChimneysACI307-08[10]计算结果进行了对比，明确规范的适用范围，并为类似工程的抗风设计提供依据和参考。

1 风洞试验及数据处理方法

1.1 刚性模型风洞试验

本试验在交通运输部天津水运工程科学研究所的TKS-400大气边界层风洞进行。该风洞是一座水平直流吹出式单试验段风洞，风洞试验段尺寸为宽4.4 m × 高2.5 m × 长15 m，为了减小试验段内的轴向静压梯度，试验段两侧壁设置了0.195°的当量扩散角，试验段最大风速为30 m/s[11]。模拟美国规范ASCE 7-16[9]中的开阔地貌C类风场，其风速计湍流度剖面，如式(1)～(2)所示，风洞试验流场模拟基本情况如图1所示。

(1)

I(z)=0.20·(10/z)1/6

(2)

刚性模型风洞试验主要考察烟囱结构在周边建筑设施干扰下的风力(表面压力及基底力)。根据建筑图对缩尺刚性测压和测力模型进行制作，同时根据场地总平面图同比例对周边建筑设施模型进行制作。根据ASCE7-16[9]，在满足缩尺模型几何相似的情况下，按照风洞截面阻塞比不超过5%的原则，模型几何缩尺比取为1∶200。测压模型在烟囱表面每隔10 m布置10～20个测点，共计测点数377个，各层测点选用不同长度的PVC测压管，管长从0.30 m变化到1.65 m，在数据处理时进行了频响修正。测力模型模拟烟囱的气动外形，底部设置与测力天平连接底座，测量烟囱的脉动基底风力。为模拟烟囱在高雷诺数流场的作用，参考ESDU[12]数据进行表面刻痕。

进行测压试验时，采用PSI压力扫描阀对测点的脉动压力进行同步采集，压力扫描阀采样频率为330 Hz；测力试验时，采用ATI测力天平对模型基底风力进行测量，采样频率为1 000 Hz。采样时长为90 s，根据斯托罗哈相似准则换算，对应于实际的32 min。

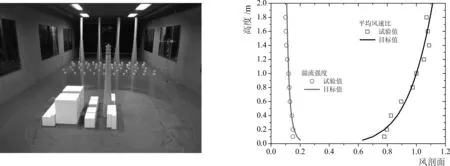
1-a 风洞试验布置照片1-b 大气边界层风剖面模拟情况

1.2 试验数据处理方法

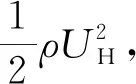
(3)

对风压系数进行统计，得到平均风压系数与均方根风压系数如式(4)～(5)所示。

(4)

(5)

图2给出了在不考虑周边建筑物影响下，烟囱2/3高度处的风压系数的分布图，并将本文试验结果与不同雷诺数下相关圆柱类结构实测数据[4]对比。由图可以看出，本实验对烟囱刻痕的处理能够模拟高雷诺数流场对烟囱的作用。

测力试验所得到的基底风力和力矩时程Fi(tk)、Mi(tk)(本项目主要考察x、y向，因此i=x，y)无量纲化为体轴风力(矩)系数时程，如式(6)～(7)。

(6)

(7)

式中：A为模型迎风面积，H为模型高度。将测压试验得到的风压力Pi(tk)按式(8)～(9)进行积分，也可得到体轴风力(矩)系数时程

(8)

(9)

式中：Ai为测点i的附属面积，Hi为测点i的高度，θx,yi为测点i在x、y方向上的法向量。

按上述方法得到的测压实验与测力实验风力系数进行对比如图3所示。由图可见，测压试验结果与测力试验结果较为吻合，验证了试验结果的准确性。

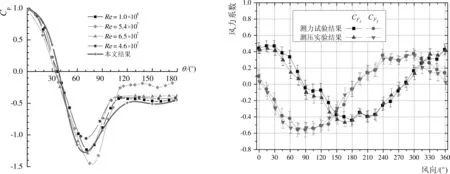
图2 试验结果与实测数据的对比

图4 风力体型系数沿高度的变化

风洞试验得到的各个高度上的风力体型系数见图4，由图可见，当不考虑周边干扰效应时，单烟囱风力体型系数沿高度的分布较为均匀，在烟囱顶部数值较大，与美国规范ACI307-08建议值较为接近。考虑周边建筑的干扰最不利风向出现在90°风向，两侧建筑正面迎风对气流形成阻塞，狭道效应使得烟囱底部风力体型系数增加，从而导致该风向下烟囱受力最为不利。后续分析主要围绕单烟囱工况和干扰效应下的最不利风向进行详细分析。

2 风振响应分析及等效静风荷载

2.1 分析方法

将刚性模型测压实验得到的脉动风荷载时程加载在烟囱结构的有限元模型上，采用动力时程响应分析法对模型进行风振响应分析，采用Newmark-β法求解动力方程(10)。

(10)

式中：M、C、K为质量、阻尼和刚度矩阵，q(t)为风振响应向量，F(t)为风荷载向量。

脉动风荷载时程F(t)取自风洞试验，再根据斯托罗哈相似准则式(11)确定作用在实际结构上的加载步长及脉动风荷载时程。

(11)

式中：f为频率，L为几何尺寸，U为风速，下标m表示模型，p表示原型。风洞试验中脉动风压测量采样频率为fs(m)=330 Hz，几何缩尺比为Lm/Lp=1:200，参考高度处(对应于实际高度为270 m处)平均风速为10.0 m/s，场地50 a一遇的3 s基本风速为80 m/s，考虑重要性系数I=1.15(ASCE 7-05)，对应实际参考高度处1 h时距平均风速为92.6 m/s。根据式(11)可得作用在实际结构上的加载频率为fs(p)=15.28 Hz，加载步长为65.45 ms。设定风荷载的加载步数为10 000步，相当于实际结构风致动力分析的总加载时间为654.5 s(大于10 min)。

计算结构风振响应采用瑞利结构阻尼，其式如下

C=aM+bK

(12)

(13)

5-a 有限元模型 5-b f1=0.43 Hz 5-c f2=1.60 Hz 5-d f3=3.58 Hz

式中：a和b分别为瑞利阻尼中的常量。由结构的阻尼比(ξ，根据ACI307-08，取0.015)和结构前两阶自振频率(ω1和ω2)采用式(13)计算得到。根据模态分析，结构前三阶振型及频率如图5所示。

(14)

式中：g为峰值因子。对于横风向等效静风荷载，按照ACI 307-08和GB50051-2013中建议的方法，以基底横风向极值力矩为等效目标，按照一阶振型的分布形式反推到各标高得到。

6-a 顶点位移响应6-b 基底弯矩响应

2.2 分析结果

采用风洞试验数据对该烟囱进行风振响应分析，得到顶点位移响应时程、基底弯矩响应时程如图6所示。经统计分析，最不利风向下烟囱结构顺风向极值位移404.4 mm，横风向极值位移为412.4 mm，位移组合值为454.3 mm，小于ACI 307-08烟囱结构在风作用下的侧向最大位移限值0.04H/12=900 mm；最不利风向下烟囱结构顺风向极值剪力为3.374×104kN，横风向极值剪力为3.081×104kN，剪力组合值为3.612×104kN；顺风向极值弯矩为5.078×106kN·m，横风向极值弯矩为5.090×106kN·m，弯矩组合值为5.666×104kN·m。

对于顺风向等效静风荷载，分别以基底弯矩为等效目标按式求得的风振系数为1.92，顺风向和横风向等效静风荷载将在下一节与中美规范对比给出。

3 等效静风荷载的中美规范对比

3.1 中国规范计算方法

对于顺风向等效静风荷载wkl，采用中国《建筑结构荷载规范》(GB50009-2012)[7]的计算方法，由下式表示

wkl=βzμsμzw0

(15)

式中：w0为基本风压，μz为高度变化系数，μs为风荷载体型系数，βz为风振系数，按下式计算

(16)

式中：g为峰值因子，I10为10 m高度处的湍流强度，Bz为背景分量因子，按式(17)计算，R为共振分量因子，按式(18)计算。

(17)

式中：H为烟囱的高度，k、a1为与地面粗糙度相关的系数，对于港口烟囱结构分别取1.276和0.186，φz为振型系数。

(18)

根据中国《烟囱设计规范》(GB50051-2013)[8]，当雷诺数Re(= 69 000UD)≥ 3.5×106且1.2UH>Ucr=f1D/St时(St为无量纲旋涡脱落频率，对于圆形结构取值为0.2～0.3)，横风向共振等效静风荷载wkc按下式计算

(19)

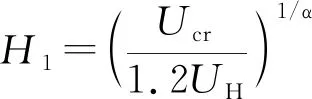
当烟囱发生横风向共振时，横风向共振荷载与对应风速下的顺风向等效静风荷载进行平方和开根号组合。

3.2 美国规范计算方法

美国建筑结构荷载规范ASCE7-16[9]中给出的顺风向等效静风荷载采用阵风荷载因子法，其计算公式为

(20)

式中：Gf为阵风荷载因子，由式(21)计算。

(21)

式中：gQ、gR和gv分别为背景、共振响应和脉动风速的峰值因子，I为高度0.6H处的湍流强度，Q为背景效应因子，R为共振效应因子。

根据美国混凝土烟囱设计规范ACI307-08[10]，烟囱结构顺风向等效静风荷载wkl由平均和脉动两部分组成，表示为下式

(22)

(23)

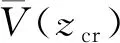
(24)

(25)

式中：Bw=0.1+2/ln(45.6H)为谱带宽参数。根据一阶模态计算各高度上的横风向风荷载，再和顺风向风荷载进行平方和开根号组合，得到结构的组合风效应。

3.3 对比分析

图7给出了风洞试验得到的等效静风荷载与中美规范计算结果的对比。顺风向等效静风荷载如图7-a所示。可以发现，由于中国规范GB50009-2012[7]中所采用的湍流强度0.14、峰值因子2.5小于美国规范取值(湍流强度0.20、峰值因子3.4)，阻尼比取值0.05大于美国规范0.015，因而计算结果较小。图中还给出了以中国规范为基础，上述参数取值参见美国规范的计算结果(GB 修正参数)，发现与ACI307-08[10]计算结果吻合较好，验证了规范中计算方法的一致性。ASCE7-16[9]与其他规范结果差异较大是由于其脉动风荷载按照阵风因子简化，与实际存在一定差异。由图可见，单体烟囱风洞试验结果与规范计算值较为接近，但规范未能考虑周边建筑引起的干扰放大效应。

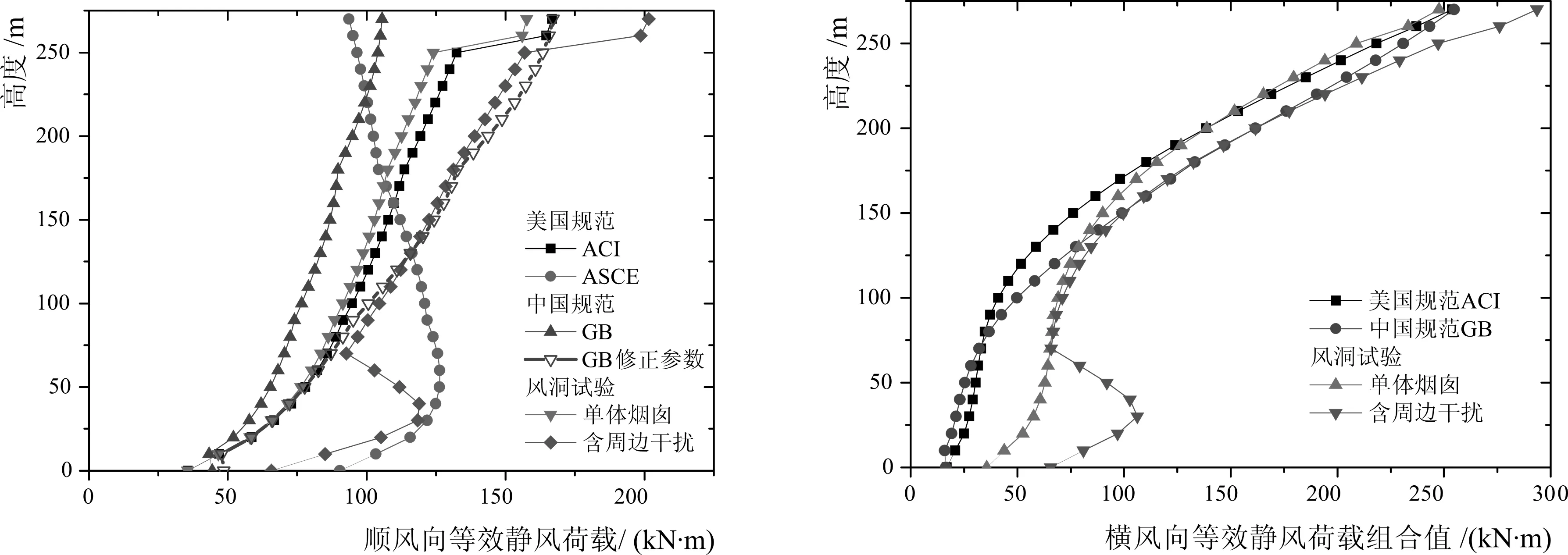
7-a 顺风向7-b 横风向(组合值)

图7-b给出了横风向组合等效静风荷载结果，可以发现，中美规范中的横风向等效静风荷载均是按一阶振型分布的，将阻尼比统一取为美国规范所规定的0.015后，中国规范计算结果略大于美国规范，总体看来二者与单体烟囱风洞试验结果较为吻合，但未能考虑周边建筑对烟囱下部的平均风荷载的放大效应。

4 结论

通过风洞试验得到的单体烟囱等效静风荷载结果与规范计算值较为接近，但由于烟囱周边的附属设施及建筑对烟囱风荷载可能产生放大效应，应在设计中予以重视。对于横风向等效静风荷载的考虑，尤其是当设计风速大于临界风速时，需要对设计风速内一定范围内横风向风振效应进行综合考虑，搜索最不利横风向组合风效应。中美规范计算的差异主要体现在对风场湍流度、峰值因子、阻尼比的取值差异，其中影响最大的是阻尼比的取值，建议后续开展相应的实测工作，得到实际烟囱结构的阻尼特性，更好地指导结构抗风设计。