线路工程带状走廊三维地形构建及轻量化研究

宋伟华，谭衢霖，夏 宇，祝 清

（1.北京交通大学 土木建筑工程学院，北京 100044；2.北京交通大学 线路工程勘测空间信息研究所，北京 100044）

三维地形建模和可视化是在计算机上对地形数据进行三维显示、模拟仿真、简化、多分辨率表达和网络传输的一项技术，它涉及到测绘学、现代数学、计算机三维图形学、计算几何、地理信息系统、虚拟现实、科学计算可视化、计算机网络等众多学科领域[1]。利用计算机三维可视化技术，将遥感影像和数字高程模型（DEM，Digital Elevation Model）相叠加，可以建立逼真的三维地形环境[2]。

在三维地形建模和可视化研究方面，文献[3]研究了基于三角形网格的地形建模的基本理论和方法,包括规则数据的三角网生成以及不规则三角网（TIN，Triangulated Irregular Network）的生成算法；文献[4]应用遥感影像与DEM数据，基于Infraworks平台建立了某线路段地形、构造物、沿线附属设施等三维可视化模型；文献[5]通过层次细节技术和基于网格的模型简化技术对三维地形建模进行简化，并且对该技术进行了相应的改善，从而能够更好地实现三维地形建模简化技术的应用。

为了满足实时三维绘制与漫游的需求，减少数据量，且保证数据的必要精度，本文主要针对三维地形空间数据的海量特性，试验了三维地形构建的2种常用表达模型，并对其轻量化处理方法进行了研究。

1 DEM数据

1.1 DEM数据概述

DEM是用于构建线路工程三维地形的重要信息之一，它描述了地面高程信息，是对地形表面形态的离散化数字表达[6]。线路是一个狭长带状构造物，三维地形建模仅需线路中线两侧一定宽度内的DEM数据，可根据直线、曲线、多边形等不同的提取方法来提取所需范围内的地形模型数据。

1.2 DEM数据获取

DEM的获取方法主要有地面测量、航空摄影测量、卫星立体测图、卫星定位测量、采集现有地形图、干涉雷达等[7]。DEM获取方式如表1所示。通常可直接获取的DEM数据源如表2所示。

表1 DEM获取方式列表

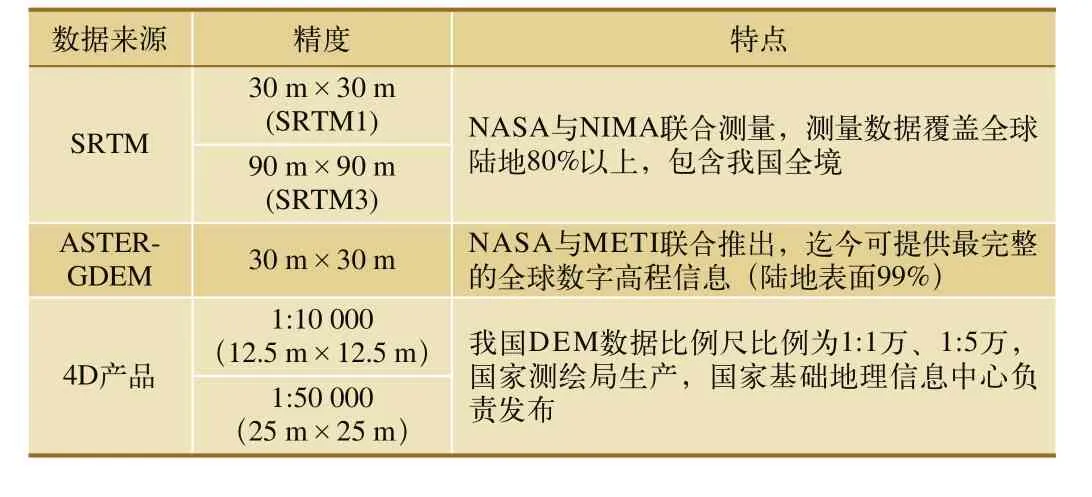
表2 DEM数据来源列表

2 地形模型构建及轻量化

2.1 地形模型表达

目前，用于线路设计的数字地形模型主要有方格网式、三角网式、离散式、分块离散型和鱼骨式模型[8]。其中应用最为广泛的是方格网式和三角网式。

方格网数字地形模型通常被分割为规则的正方形、矩形或三角形等网格，规则网格将区域空间切分为规则的格网单元，每个格网单元存储了相应的高程值，如图1 a所示。方格网数字地面模型（DTM，Digital Terrain Model）适合数据的存储、分割、合并、内插，便于计算区域内等高线、坡度、坡向、山坡阴影等地理要素，适用于分布较为规则的地形环境，在线路设计领域已成功运用于狭长窄带线路优化设计之中。但是，方格网DTM数据的分辨率单一，不能精确表示地形的结构细部，难以表达复杂地形的突变现象，在地形平坦的区域存在大量的数据冗余，造成数据量过于庞大，给数据信息管理带来诸多困难。

TIN原始数据点间无任何联系且随机分布，将地形点覆盖在数字模型区域上的三角形的各顶点，利用分布不规则的数据生成连续的三角面来逼近地形表面，高程由该点所处的三角形区域确定，如图1 b所示。TIN没有改变原始数据点，其精度高，便于表征特征性、断裂线、边界线，既适用于规则分布的数据，也适用于不规则分布的数据。

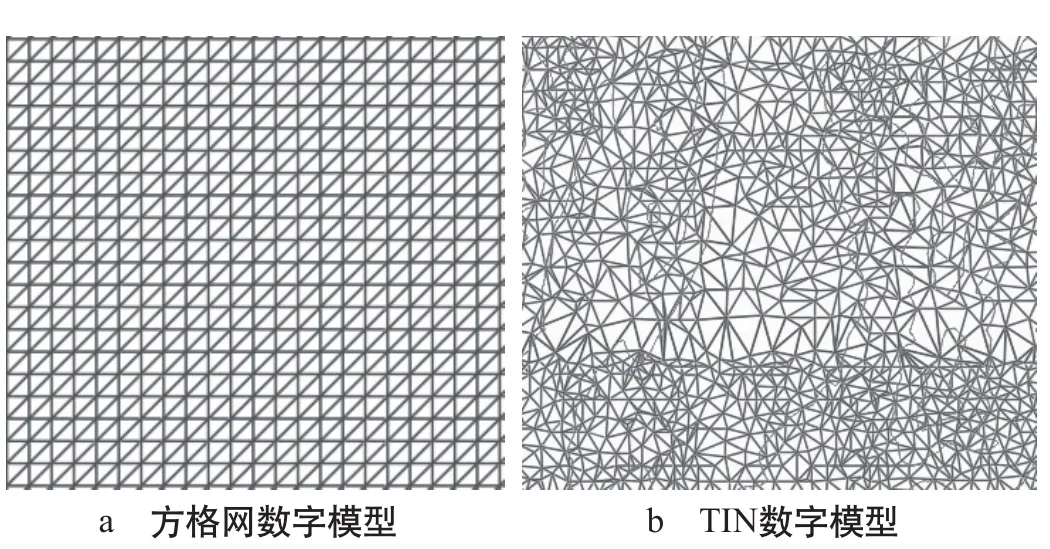
图1 数字地形模型

本文分别利用DTM和TIN数字模型建立三维地形曲面，地形曲面数据对比如表3所示。对比发现，主要曲面参数（如最小高程、最大高程）没有区别，但在最大坡率上出现了较大的变动。TIN模型能用更少的数据来精确地表示含有大量断裂线和构造线的地形表面，更精确合理地表达复杂地表形态，从而使建立的三维地形环境更为精确。故本文选用TIN进行三维地形环境建模。

2.2 Delaunay三角剖分

2.2.1 Delaunay三角剖分性质

如何把离散集合剖分成不均匀的三角形网格，即散点集的三角形剖分问题，是建立三维地形环境的关键[9-10]。实际中运用最多的三角剖分方法是Delaunay三角剖分法。Delaunay三角剖分法有2个重要性质。

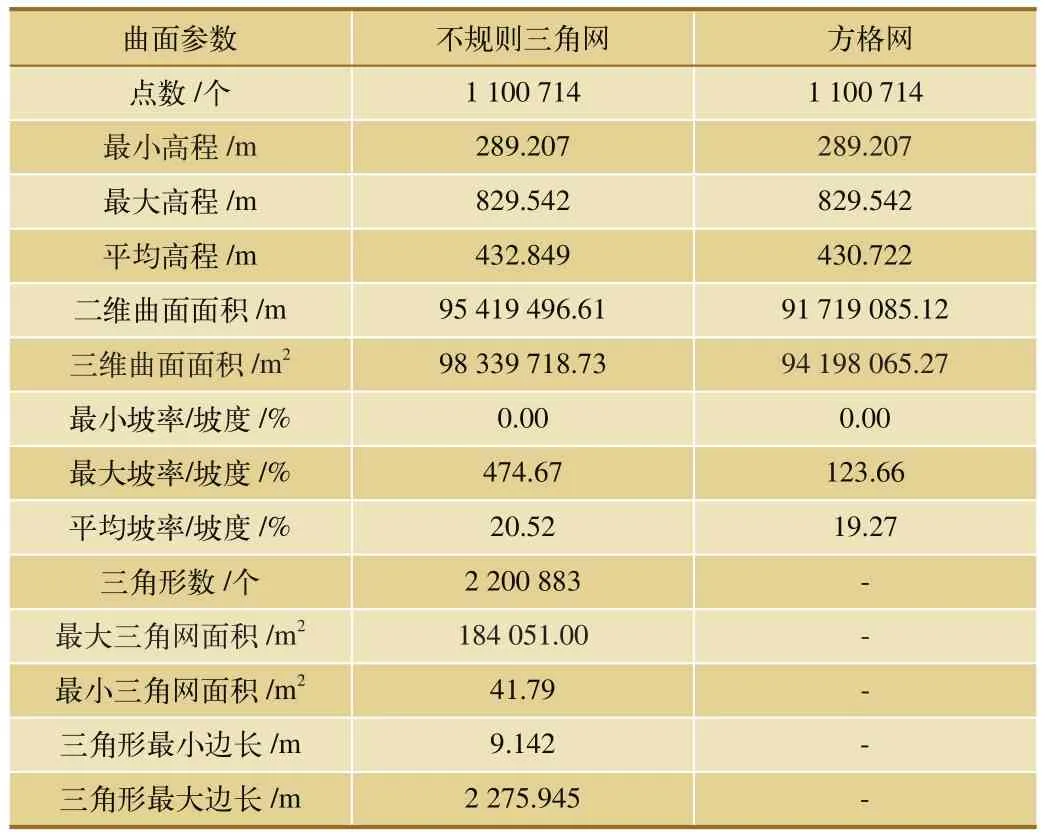
表3 不同数字地形曲面参数对比列表

（1）空外接圆性质

Delaunay三角网是一系列相连但不重叠的三角形的集合，在Delaunay三角网中任一三角形的外接圆范围内不会有其他点存在。如图2所示，设AB边是三角形ABC和三角形ABD的公共边。若D点不落在三角形ABC的外接圆内，则称AB边是局部最优化的，即该三角形具有空外接圆特性。当三角形不具备外接圆特性时，则交换对角线生成另一种三角划分，使得三角形具有空外接圆特性，该过程称为局部优化过程（LOP ，Local Optimization Procedure）。

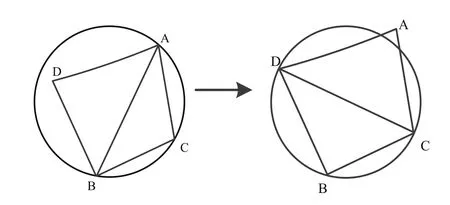
图2 局部优化过程示意图

（2）最大化最小角特性

在散点集可能形成的三角剖分中，Delaunay三角剖分所形成的三角网的最小角最大，是最接近于规则化的的三角网。其任意2个相邻的三角形构成的凸四边形，在相互交换对角线后，6个内角的最小角不再增大，如图3所示。

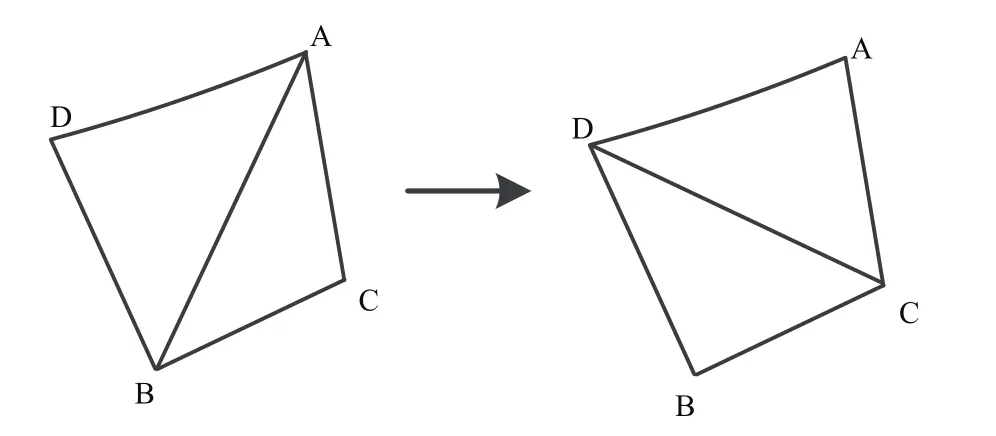
图3 最大化最小角示意图

2.2.2 Delaunay三角网生成算法

根据构建TIN算法的实现过程，可将Delaunay三角网生成算法划分为分治算法、三角网生长法和逐点插入法[11-12]。分治算法将点集划分到足够小，使其易于生成三角网，然后把局部三角网合并生成最终的三角网，划分过程中，用LOP算法保证Delaunay三角网的构建；三角形生长算法先找出点集中相距最短的2点，将其连接成为一条Delaunay边，然后按判别法搜寻包含此边的另一端点，并依次处理所有新生成的边；逐点插入法先在包含数据点的一个多边形中建立初始三角网，再将剩余的点逐一插入，用LOP算法构建Delaunay三角网。

三角网生长算法时间效率低下，目前较少采用；分治算法复杂度较优，但需要占据较大的内存空间且预处理和优化工作量较大；逐点插入法实现简单、占用内存小，但时间复杂度差、运行速度慢。由于线路工程里程较长、方案较多，为保证精度导致所取离散点数目较多，需对数字地形模型维护和更新等原因，在综合分析各算法优劣的基础上，采用内存占用较小的逐点插入算法，算法流程如下：

（1）建立初始三角网，如图4所示，给定点集的包容盒 Box（Xmin，Xmax，Ymin，Ymax）并将其剖分为2个初始三角形A，其中，Xmin为数据点X坐标极小值；Xmax为数据点x坐标极大值；Ymin为数据点y坐标极小值；Ymax为数据点y坐标极大值。

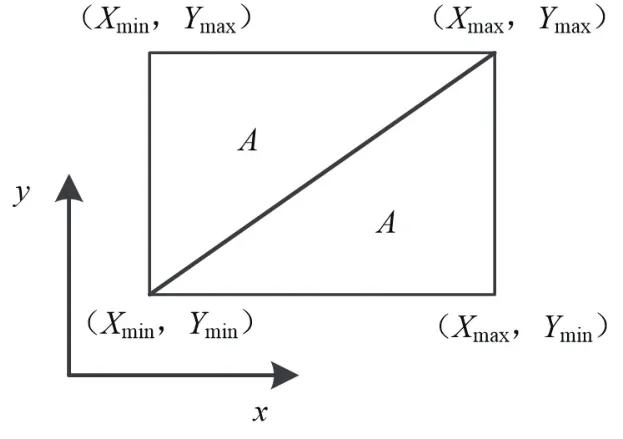
图4 初始三角形剖分示意图

（2）从点集中取出一点P，在已建立的三角网中找到包含该点的三角形进行定位，如图5 a所示。

（3）在包含P点的三角形拓扑关系中，利用空外接圆性质找出外接圆包含的三角形集合，其外边界即为要确定的影响域，如图5 b所示。设三角形abc，如图6所示，按逆时针排列，空外接圆性质判断按公式（1）计算。若F＜0，则d在外接圆内侧；若F＞0，则d在外接圆外侧；若F=0，则d在外接圆上。

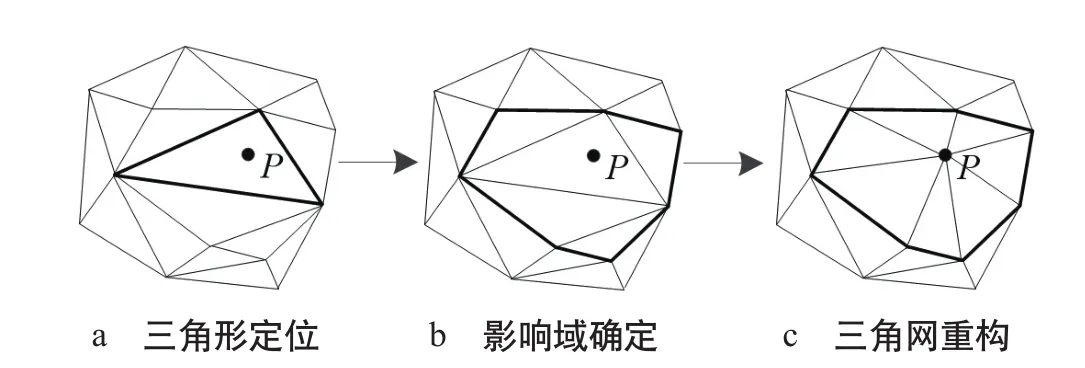
图5 插入P点重构三角网过程图

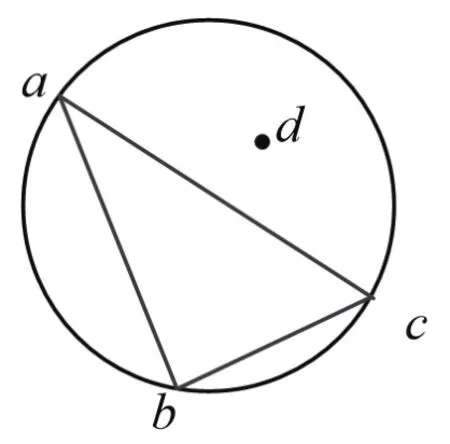
图6 空外接圆判断示意图

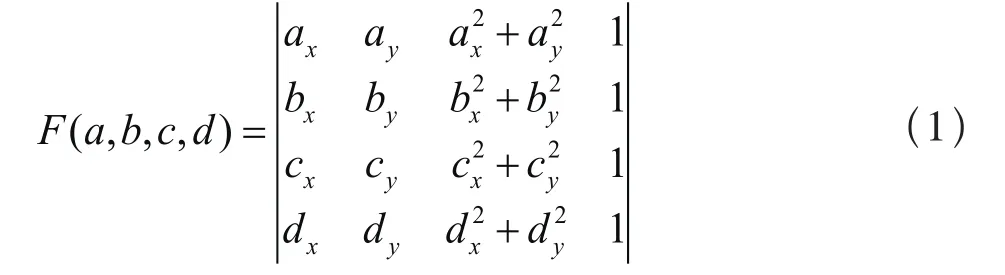
其中，ax、ay、bx、by、cx、cy、dx，dy分别为数据点a、b、c、d的横纵坐标。

（4）依据Delaunay性质在影响域内进行三角网重构，将影响域各边界交点与插入点顺次连接，即得插入点后重构的三角网，如图5 c。

（5）待所有点内插完后，删除边界冗余三角形。将获取的DEM数据根据Delaunay三角剖分算法构建TIN，建立三维地形曲面模拟地形空间分布。图7为试验区域的TIN模型，图8为三维地形曲面模型。

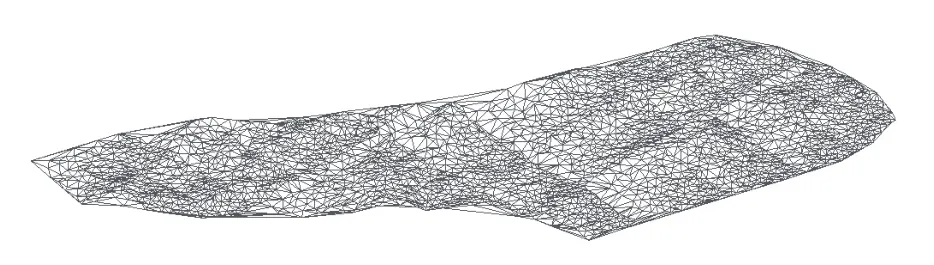
图7 线路走廊带TIN模型示意图

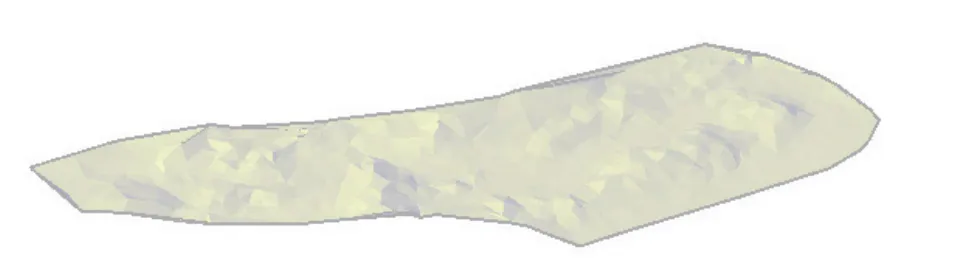
图8 线路走廊带三维地形曲面模型示意图

2.3 数据轻量化

由于线路具有工程距离长、覆盖范围广的特点，导致根据Delaunay三角剖分建立的三维地形曲面数据量较大。臃肿的三维曲面数据造成系统运行缓慢，为后续的线路设计带来困难。因此，需要对海量的数据进行简化处理来优化曲面性能，在保证地形曲面精度的同时减少数据量的冗余。数据轻量化主要有边缘收缩法和点删除法2种方式。

2.3.1 边缘收缩法

边缘收缩法使三角形的一条边收缩到单一点，每次边缘收缩可以删除一个点，同时减少2个三角形。设每个三角形平面方程为：

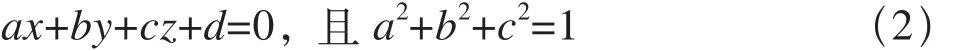
其中，a，b，c，d为三角形平面方程的系数。

定义p=[a b c d]T，则每个三角形的矩阵误差为：

顶点v的误差矩阵为环绕网格顶点周围三角面片的平均矩阵误差∑Q/n，n为环绕在网格顶点v周围的三角面片的个数，即误差为：

其中，v为三角形收缩边的顶点坐标。

三角形收缩边缘的顶点v1和v2合并到新顶点v，其边缘收缩的误差为：

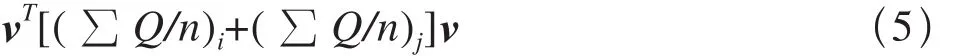
误差最小点即为新顶点，同时删除误差较大的点，方法过程如图9所示。

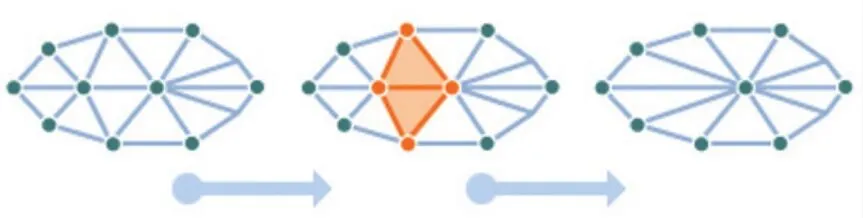
图9 边缘收缩简化示意图

2.3.2 点删除法

点删除法按照简化比例进行曲面点的选择和删除，删除三角网格中，在高程容许误差范围内，且不会导致拓扑结构改变的点。高程容许误差范围计算公式为：

其中，h为初始高程；h'为删除点后的高程；ε为容许误差。

同时对由此删除操作引起的空洞进行三角化再构建TIN，方法过程如图10所示。

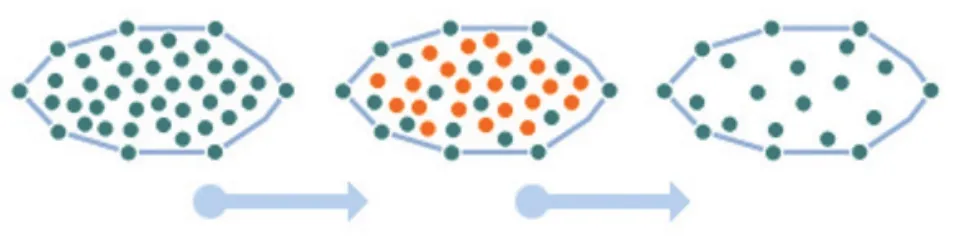
图10 点删除简化示意图

2.3.3 方法对比

基于原始DEM数据构建地形曲面，分别采用边缘收缩法和点删除法对原始地形曲面进行简化，2种方法删除点数所占百分比均为50%，详细参数如表4所示。由表4中参数对比分析可知，利用边缘收缩法简化曲面后，曲面的最大坡率、最小三角网面积等参数出现了较大波动，而利用点删除法对曲面可进行有效地简化，且曲面参数未发生明显改变，失真较小。

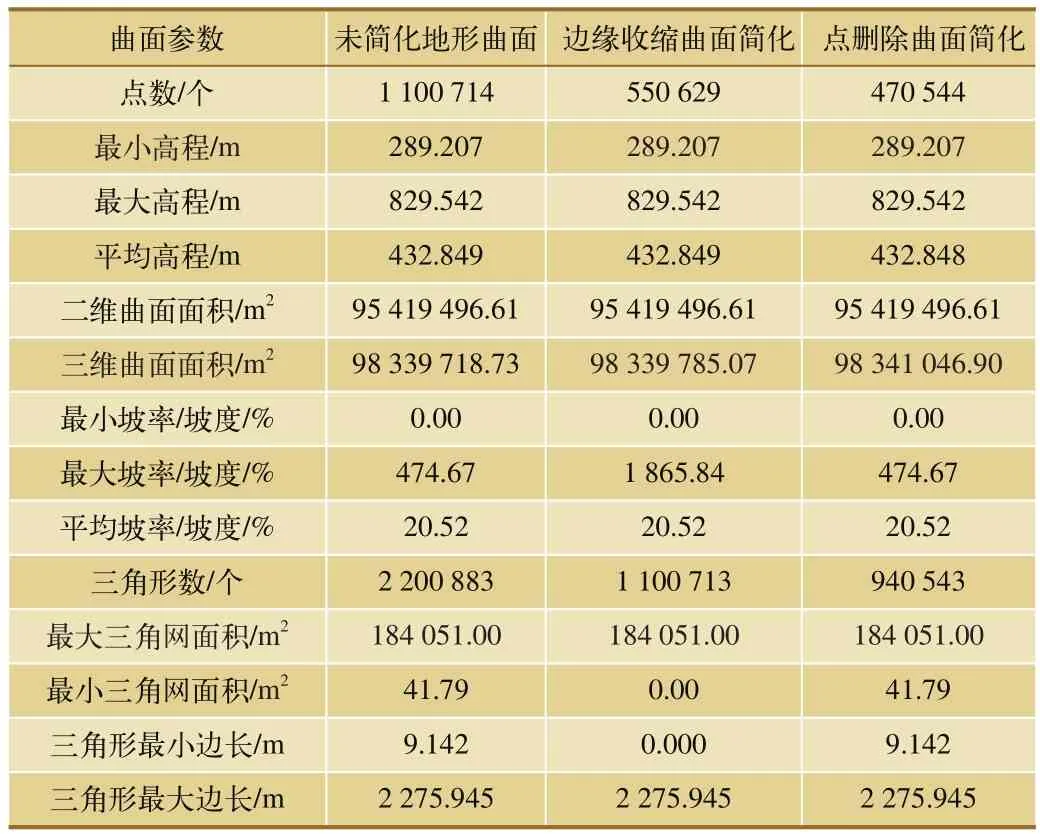
表4 三维曲面不同优化方式参数对比列表

3 结束语

随着长大线路工程数字信息化程度的提高，项目建设过程中形成的数据种类越来越多，数据量越来越庞大。研究线路工程三维模型的构建方法及有效地轻量化处理方式是线路工程数字信息化变革的技术挑战之一。本文针对三维地形空间数据的海量特性，通过Delaunay逐点插入算法构建TIN模型，实验证明该算法能够用更少的数据来合理地表达复杂地表形态，更适用于线路工程三维地形建模；对比了2种数据轻量化方法，试验参数对比表明，点删除法对三维地形模型的简化更为有效。