基于动力学仿真分析对摩托车车架结构的改进设计

唐 琳 秦睿安 孙立星

（1-天津内燃机研究所 天津 300072 2-苏州大学）

引言

摩托车在实际行驶中环境极其复杂，通常由于路况不好、负荷大以及用户操作不正确等会出现车架断裂、骑乘舒适性降低等状况。传统的设计和改进方法多采用静强度校核和试凑法，往往不能及时有效地解决问题。摩托车车架是整个车辆的支撑骨架，结构复杂，其动态特性对整车在各种负荷下的振动特性、操纵稳定性和乘坐舒适性都有很大影响。常规的有限元分析方法主要适用于复杂边界条件下形状不规则的机械结构的力学特性分析。因此，在摩托车设计初期和方案验证阶段，建立车架有限元模型，在模态分析的基础上，研究车架几何结构的振动特性和动力学特性[1-3]，可以预估车架结构在动态载荷下可能产生的振动特性和结构设计上的缺陷，优化结构设计，提高车辆整体振动特性、舒适性和安全性。

1 原车架的有限元分析

1.1 车架结构特点和受力特点

摩托车车架是整车安装基体和支撑，将发动机总成、传动系统、悬挂系统、操纵系统以及其他相关零部件连接成一个有机的整体。车架除了满足零部件安装要求，还要保证车辆行驶平稳、操纵灵活。从摩托车承受的作用力分析，车架是承受空间力系的复杂多体结构。车架承受的静载荷包括车辆的质量和要承担的载荷；车架承受的动载荷主要是发动机运转产生的激振力、车辆道路行驶中来自路面的冲击载荷以及传动系统传递的转矩。当摩托车行驶在不平坦的路面时，车架承受路面不平度产生的冲击力，会产生纵向弯曲变形；摩托车转弯行驶时，整车各系统承受各种侧压力，会产生横向弯曲变形。这些变形能改变车架上各个分总成及其零部件间的相对空间位置，进而影响某些系统的正常工作，甚至前后轮可能不在同一平面上运转，使得车辆丧失行车稳定性。上述载荷作用下车架产生的变形和振动响应，会影响车辆的操纵性、稳定性，进而影响到车辆行驶的安全性、骑乘舒适性。因此，对车架需要进行强度、刚度和动力学特性分析。

1.2 有限元法的分析方法

有限元法的基本思想是：将一个连续的弹性体划分成有限个单元的组合体，各个单元在结点处连接，设定相邻单元的有关参数具有一定的连续性。在分析连续体结构的动力学特性时，首先假设单元位移分布是结点坐标某种位移插值函数。然后建立单元的几何方程，结点位移根据位移表达式计算得出。建立单元的本构方程，通过应变表达式推导出用结点位移表示单元应力的关系式。利用变分原理，建立单元结点力与结点位移之间的关系式，也称为单元的平衡方程。所有单元的平衡方程集合在一起，组成整个连续体的平衡方程。求解该平衡方程组，解出未知位移，根据求得的结点位移计算出各单元位移，进而求解各单元的应力。

对车架进行动态分析时，首先建立每个单元的振动微分方程。然后将各单元的惯性力向量、阻尼力向量、弹性力向量和载荷向量迭加，得到对应于整体车架的质量矩阵、阻尼矩阵、刚度矩阵以及载荷向量，最后得出整体车架的动力方程式，即用有限元法求解车架振动问题的基本方程。

车架固有振型及其主振型属于车架的固有特性，求解车架振动问题的基本方程时，取载荷向量为0。另外，由于车架结构阻尼小，对其固有频率影响很小，通常忽略不计。则车架振动问题的基本方程就变成了车架结构无阻尼自由振动的微分方程，这是一个常系数齐次微分方程，求解其特征方程，可解出n个特征值，即此离散模型的n 个固有频率。对应每阶固有频率，可以求出对应的特征向量，即车架的几个主振型。

通常情况下，结构固有频率在结构受到干扰时是易于发生振动的频率。结构在固有频率下的变形为主振动模态，即主振型。固有频率、主振型反映结构动力学特征，决定结构对动力载荷做出的响应。

1.3 车架结构的自由模态分析

基于有限元的模态分析特点，对车架结构自由模态下各固有频率和主振型进行分析，根据振动特性、应变、应力和振型特点，预估常用行驶工况下可能出现结构振动的工况。

建立车架有限元模型的步骤如下：

1）车架结构的适度简化。本文的车架结构由于功能性特点，几何结构比较复杂，车体采用弯曲钢管、复杂钢板焊接结构。进行有限元模态分析前，需要适度简化车架结构，对于对模态分析影响不大的零部件进行删除，保留车架主体结构和主要零部件。原车架三维数字化实体模型见图1。

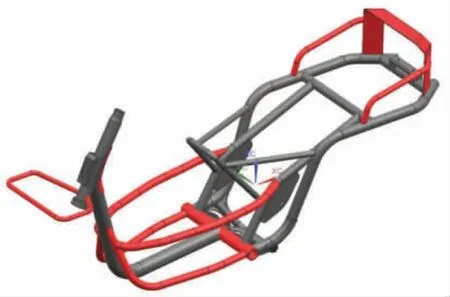
图1 原车架结构几何模型

2）有限元网格的划分。通常，有限元网格划分的合理性关系到数值计算的精确性及可行性。分析车架几何拓扑特性，并尽可能简便合理，对车架结构进行网格划分，这样可以提高运算效率。本车架结构的网格采用四面体单元，符合摩托车车架零部件三维模型具有复杂几何特征的特点，可以较好地表达结构特征。含有中间结点的四面体单元计算精度较高，得到的结果可信度较高。

3）定义材料及其特性。定义车架有限元模型中网格结构的材料，设定材料特性值。车架材料为碳素结构合金钢Q235，其弹性模量E=206 GPa，泊松比为0.3，密度为7.85 kg/dm3，屈服强度为235 MPa。

4）确定边界条件。通常情况下，在自由边界条件下得到的模态值，可以通过对数学模型进行计算得到任意边界约束条件下的特性分析，反之则不行。因此，本文采用自由边界条件下的有限元模态分析，不施加约束与力，计算车架的自由模态，得到车架主体结构固有频率及相应模态振型。

计算出的原车架结构主频率和主振型描述见表1。

图2 为原车架结构第2、4 阶振型（车架绕y 轴弯曲），图3 为原车架结构第3 阶振型（车架绕x 轴扭振）。

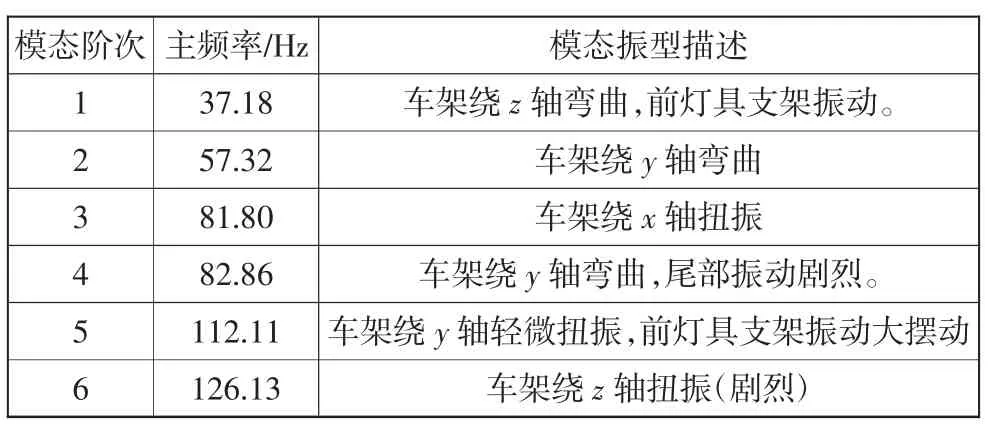
表1 原车架结构模态主频率及其振型

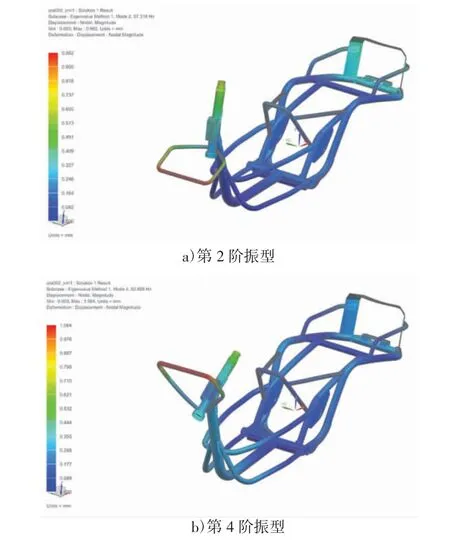
图2 原车架结构第2、4 阶（车架绕y 轴弯曲）振型

图3 原车架结构第3 阶（车架绕x 轴扭振）振型

从图2 可以看出，第2、4 阶振型表现为车架绕y轴弯曲。在这种弯曲变形的振型下，车辆纵向行驶中，受到来自地面的冲击力或进行制动时，可能出现共振现象，对车架某些结构产生破坏或潜在损伤，影响行驶的舒适性。从图3 可以看出，第3 阶振型表现为车架绕x 轴扭振。当车辆转弯行驶时，这种振型可能使车架产生横向弯曲变形以及共振现象，导致摩托车行车稳定性出现问题，产生侧滑或者影响操控性。

2 改进后车架结构的自由模态分析

2.1 车架结构改进

在车架结构改进设计过程中，主要针对有问题的固有频率及其主振型的变化情况，分析其模态应变能的表现特性，确定车架待改进的几何结构或安装用的零部件支架结构。通常，高应变能的单元表明高弹性变形的区域，这些单元对模态变形影响最为直接[4]。因为，高应变能单元对固有频率和振型的影响较大。因此，主要分析模态响应的应力或位移有问题的结构，根据功能性特点和机械设计原理来确定结构优化设计的方案。基于原车架结构设计方案的有限元分析结果，分析和观察车架的主振型图，找出车架上结构设计存在问题的零部件。对车架主体结构进行针对性改进，修正其不合理的几何结构，以增加车架主体结构的刚度来改善某些车架在主要行驶工况下的固有频率。

车架结构的主要改进方案包括：改变车架中间的主梁壁厚，从2.5 mm 增加到2.8 mm，并且改变其上的加强板几何尺寸和结构形式。旧方案中的加强板在模态分析中应力和应变的能量都比较大，改进后，增大了几何尺寸和弯曲位置的圆角半径；在车头管上灯具支架的薄弱处，根据其他零部件的安装特性和功能约束条件，增加了合理的加强板，既增加了强度和刚度，也没有对整车质量产生影响；改进了车架尾部的电器安装主支架及其附属小支架，把薄板结构改成了弯管，增加了其刚度和强度，且不影响质量和安装要求。

图4 为改进车架结构的几何模型及主要改进位置的描述。

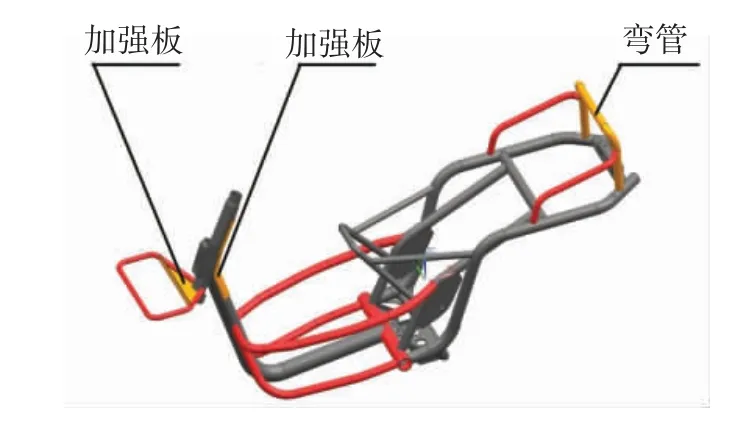
图4 改进车架结构的几何模型

完成车架上各处模态振型问题较大结构的优化改进，再次进行车架模型模态分析，其有限元模态分析和动态响应分析保持与初级模型分析方法的一致性。对改进车架进行自由模态分析，求出改进车架无阻尼情况下各个主振型和主频率。改进车架结构主频率见表2。

表2 改进车架结构模态主频率及其振型

图5 为改进车架结构第2、4 阶振型（车架绕y轴弯曲），图6 为改进车架结构第3 阶振型（车架绕x轴扭振）。

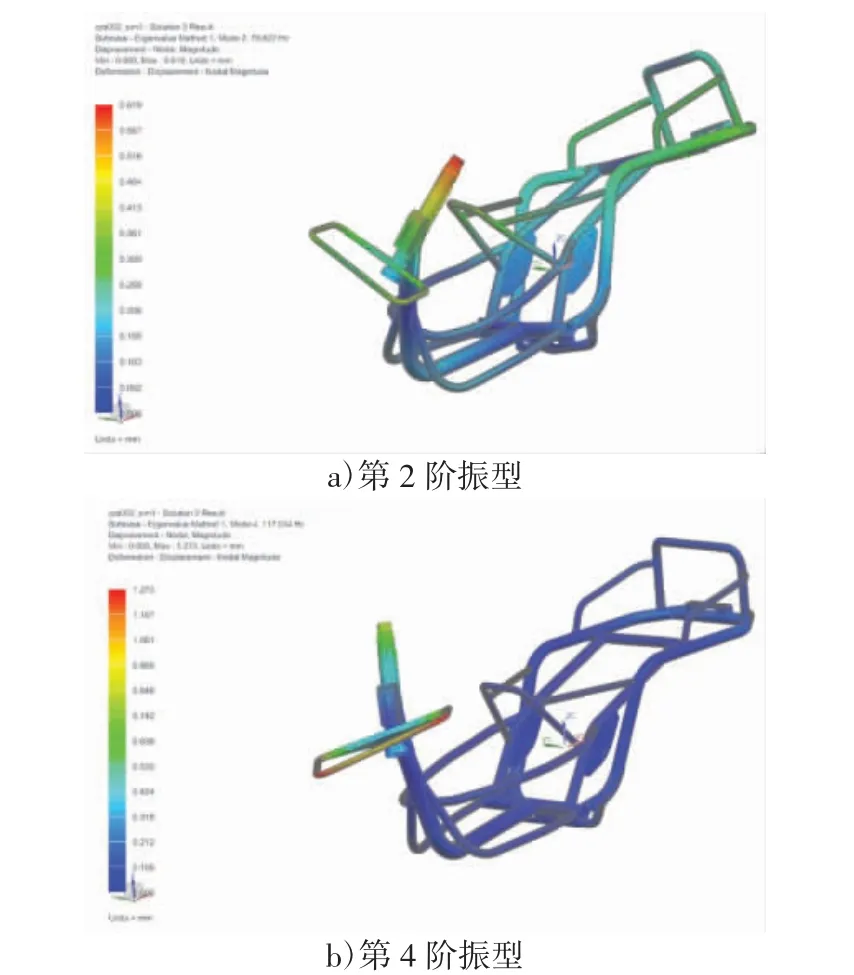
图5 改进车架结构第2、4 阶（车架绕y 轴弯曲）振型

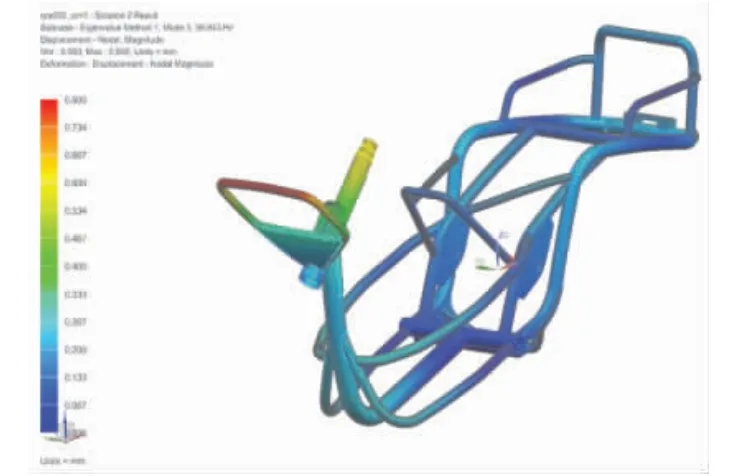
图6 改进车架结构第3 阶（车架绕x 轴扭振）振型

从图5 可以看出，第2 阶振型与原车架的振型不同，表现为车架绕y 轴扭振，且主频率提高，避开了低频振动情况；第4 阶振型与原车架的振型相同，表现为车架绕y 轴弯曲，但程度低于原车架，且主频率提高，避开了低频振动情况。从图6 可以看出，第3阶振型与原车架的振型相同，表现为车架绕x 轴扭振，但程度低于原车架，且主频率提高，避开了低频振动情况。

2.2 计算结果分析

对表1 与表2 所示的基础振型进行对比分析，可以看出，改进后，对于第1 阶振型，车架绕z 轴弯曲的主频率从37.18 Hz 变为59.59 Hz，提高了60.27%；对于第2 阶振型，车架绕y 轴弯曲变为绕y 轴扭振，主频率从57.32 Hz 变为79.82 Hz，提高了39.25%；对于第3 阶振型，车架绕x 轴扭振的主频率从81.80 Hz 变为98.94 Hz，提高了20.95%；对于第4 阶振型，车架绕y 轴弯曲的主频率从82.86 Hz 变为117.03 Hz，提高了41.24%；对于第5 阶振型，车架绕y 轴轻微扭振变为绕z 轴轻微扭振，主频率从112.11 Hz 变为139.98 Hz，提高了24.86%；对于第6 阶振型，车架绕z 轴扭振变为绕y 轴轻微弯曲，主频率从126.13 Hz变为141.58 Hz，提高了12.25%。因此，从改进车架结构的基础振型来看，改进后，较大地改善了车架的力学特性。

可见，改进后，对低频率的主频率改进都较大，尤其避开了81.80 Hz 和82.86 Hz 两个主要共振频率，使得常用行驶工况下的舒适性得到了很大的提高。对常用行驶工况具有影响的共振频率从5 个减少到3 个。第5 阶、第6 阶两个最高主频率提高到了139.98 Hz 和141.58 Hz，基本不在常用的行驶工况范围内，可以不予考虑。通过对车架上存在问题的主振型进行分析，改进涉及到的几何结构和安装零部件的结构件，从而改进了车架的主频率和主振型，达到了改善其动力学特性的目的。

3 结论

车架结构设计既要求几何结构简单合理，又要求材料及工艺能保证车架力学特性符合要求。在车架的设计初期或验证阶段，建立规范的设计方法和分析方法，利用有限元分析法对车架进行模态分析，研究车架的静力学和动力学特性，保证车架结构符合设计要求，满足静载荷、动载荷下动力性、安全性、操纵性等要求，在设计阶段完成车架结构的优化，缩短设计时间和节约成本，并保证设计开发的正确性、适应性。