运用地下水水位对多频潮汐的响应识别含水层的压力传导系数

阳 玲，张 铭，郝永红

（1.天津师范大学 数学科学学院，天津 300387；2.天津师范大学 天津市水资源与水环境重点实验室，天津 300387；3.日本地质调查局，筑波茨城 日本 305-8567）

随着中国沿海城市经济和社会的快速发展，陆源污染物无论从种类上还是数量上都呈上升趋势，海洋污染物总量的85%以上来自陆源污染物.研究人员对大西洋海湾地下水中镭同位素的示踪研究表明，滨海地区地下水海底排泄量相当于入海河流水量的40%，但其携带的污染物浓度却是地表水浓度的几十倍甚至上百倍[1-2].地下水携带的大量陆源污染物（化肥、农药和重金属等）通过海底排泄进入滨海水域，造成近岸海域水质恶化，引发赤潮和绿潮等一系列海洋生态灾害和环境突发事件.在地下水海底排泄过程中，含水层的水力特性起到关键性作用，因此，识别含水层水力参数是实现滨海及近海海域生态环保的关键.压力传导系数是地下水系统中溶质运移和扩散的重要参数之一，通常由抽水试验确定，即通过抽水和注水对地下水系统产生扰动（刺激），利用地下水位的响应计算压力传导系数.此方法的不足之处在于抽水试验需要耗费大量的人力、财力和物力[3].海水潮汐作为一种自然刺激，同样会引起含水层地下水位的波动.因此，本研究将地下水水位对潮汐的响应看作是一种天然抽水试验，以期利用地下水水位对潮汐的响应识别含水层压力传导系数，提出一种经济实用的识别滨海地区含水层压力传导系数的新方法.

1 模型建立和解析解

潮汐由万有引力和地-月系统绕其共同质心旋转的综合作用造成，通常由多个分潮构成，因此又称多频潮汐.潮汐的多频信号在含水层中传播，只有最强的信号可以穿过含水层引起地下水水位的变化，并且能够被地下水水位压力感应器所捕获.同时，由于含水层的过滤作用，较弱的潮汐信号会在经过含水层时衰减消失.在以往地下水与海水交互作用的研究中，人们主要关注信号最强的单频潮汐，相关研究如表1 所示.从数学角度考虑，多频谱波动潮汐可以表达为

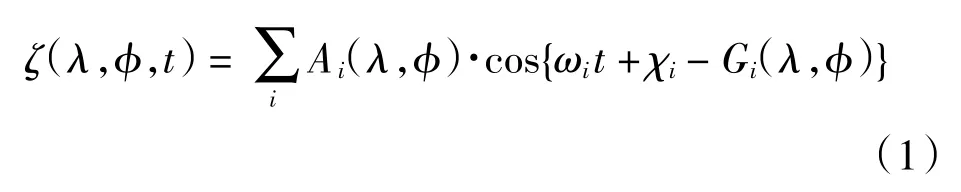
式（1）中：λ和φ分别为经纬度；Ai（λ，φ）为振幅；Gi（λ，φ）为相位；χi为初始相位.

研究表明，式（1）的前2 项即可描述98%的潮汐特征[4-5].由此可见，双频潮汐可以更加准确地描述海水的周期波动.为了更加全面、准确地反映地下水水位对潮汐的响应，本研究在解析过程中选择2 个分潮.

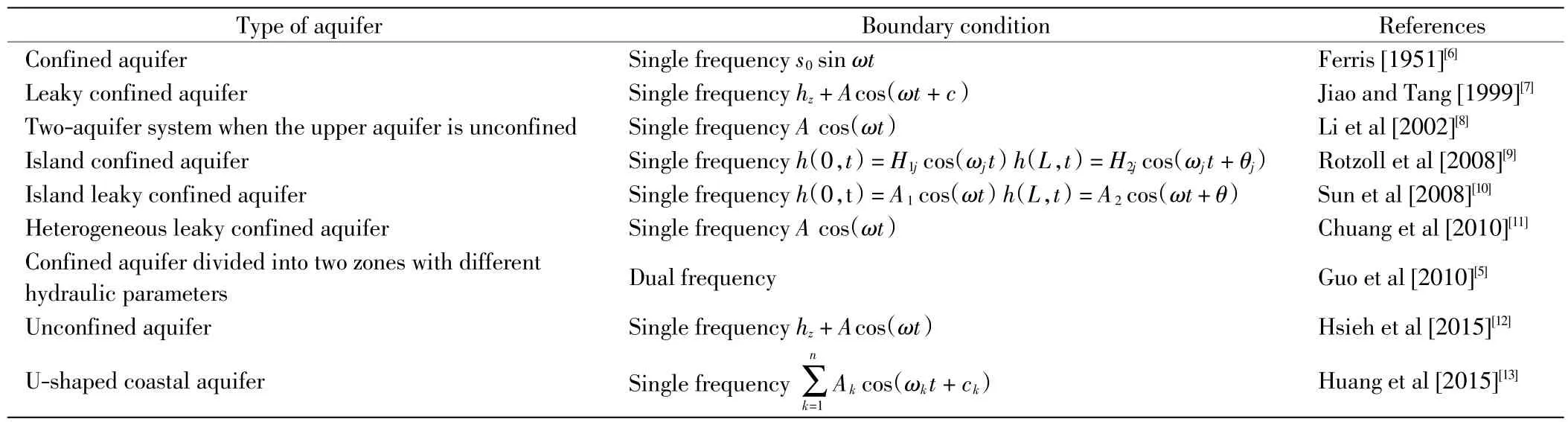
表1 各种含水层以及边界条件Tab.1 Various aquifers and boundary conditions

本研究考虑的滨海地下水系统包含上、下2 个弱透水层及其中间夹层，即含水层.假设每一层均均匀且水平，系统可以概化为一维地下水流动概念模型，示意图如图1 所示，其中x 轴的起点位于垂直海滩与不透水层底板的交叉点，x 轴向陆地为正方向.以平均海水水位（mean sea level，MSL）为基准，双频潮汐振幅分别为A1和A2.

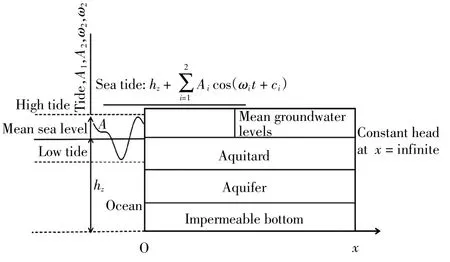
图1 无限宽海岸含水层示意图Fig.1 Schematic diagram of an infinite wide coastal aquifer

在这些假设下，承压含水层中一维地下水流动的控制方程为

式（2）中：h 为地下水水位；x 为水平坐标；t 为时间；T为含水层的渗透系数；S 为含水层储水系数.式（2）严格应用于承压含水层，但当地下水振荡比含水层厚度小时，式（2）可用于非承压含水层[5，14-16].

潮汐边界条件为

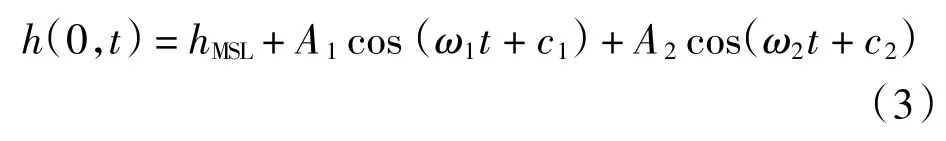
式（3）中：h（0，t）为 x=0 处的地下水水位；Ai为潮汐振幅（i=1，2）；hMSL为平均海水水位；ωi为潮汐振荡的角速度（i=1，2）；ci为潮汐振荡的初始相位（i=1，2）.

无穷远处，无流量边界条件为

式（4）中：h（∞，t）为内陆离海岸无穷远处的地下水水位.式（4）表明，海水潮汐信号在含水层的传播过程中具有衰减效应，当距离海岸线无穷远时，潮汐对地下水水位的影响为0[7].

依据文献[7]，将式（1）～式（3）扩张到复数域上求解，结合解的叠加原理，获得地下水水位对潮汐响应的解析解

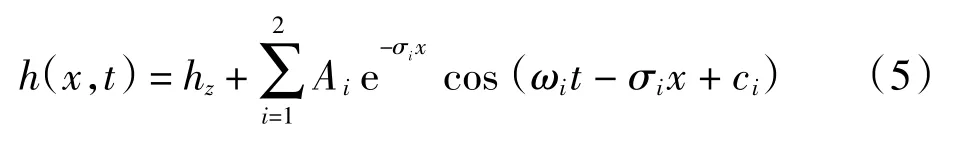
2 数值模拟

2.1 地下水对潮汐的响应

为了模拟地下水水位对海洋潮汐的响应，根据实际情况，在参数的合理取值范围内，对式（5）中参数进行赋值，具体参数值如表2 所示.

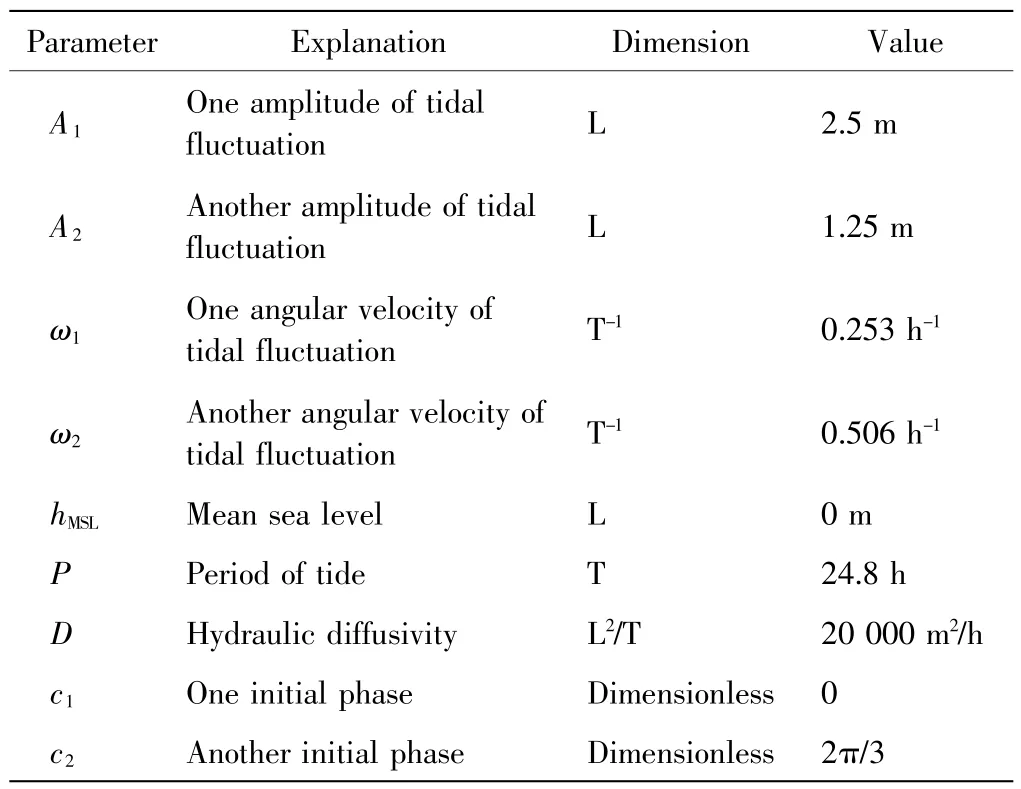
表2 含水层参数Tab.2 Parameter of aquifer

基于表2 中的参数，得到地下水水位变化对海洋潮汐的响应情况.图2 描述了地下水水位h 随x 和t变化而变化的过程.由图2 可以看出，地下水水位h是关于时间t 和距离x 的二维函数.x 越小（靠近海岸），地下水水位对潮汐的响应越大，x 越大（远离海岸），地下水水位对潮汐的响应越小，即随着距离的增加，地下水振幅逐渐衰减，至无穷远处稳定于平均海水水位.

为了更加清楚地了解地下水水位对潮汐的响应过程，分别给出x=0、100 和200 m 时，地下水水位对潮汐的响应情况，结果如图3 所示.由图3 可以看出，当x 较大（x=200 m），即远离海岸线的地方，地下水水位较低，波动较小.相反，当x 较小（x=100 m），即靠近海岸线的地方，地下水水位较高，波动较大，反映出潮汐信号在含水层中的传播与位置x 和时间t 有关.

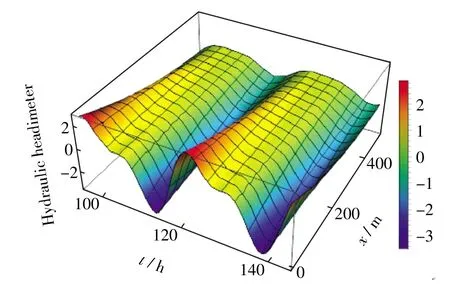
图2 地下水对潮汐的响应Fig.2 Response of groundwater to tides

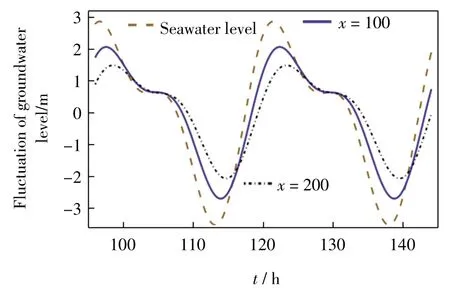
图3 当x=0、100 和200 m 时，地下水水位随时间的变化Fig.3 Variation of groundwater level with time when x= 0，100 and 200 m

2.2 用最小二乘法识别压力传导系数

本研究的主要目的是运用解析解和数值模拟相结合的方法，验证利用潮汐信号和地下水水位响应识别含水层的压力传导系数的可行性.首先，在x=200 m处选取t∈[96，121]时间段的地下水水位的101 个离散点，时间步长为0.25 h.然后，为了模拟实际地下水水位数据中由于设备和人为因素会造成的误差，在离散点上分别叠加 N（0，0.12）和 N（0，0.052）的高斯白噪声，生成地下水水位的仿真观测数据，即获得hm=h（x=200，t+ Δt，D=20 000）+N（0，0.12）和 hm=h（x=200，t+ Δt，D=20 000）+N（0，0.052）共 2 组仿真观测数据，如图4 所示.最后，基于仿真观测数据，运用最小二乘法，估计压力传导系数，误差函数为

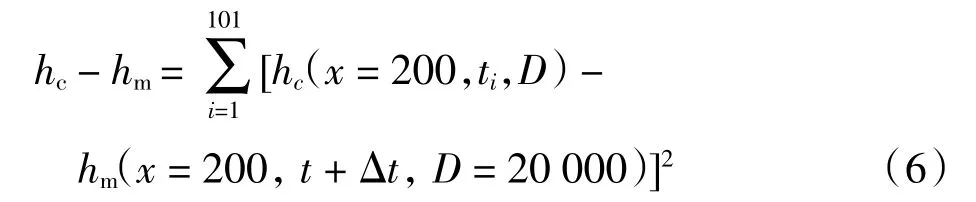
式（6）中：hc为计算数据；hm为仿真观测数据.

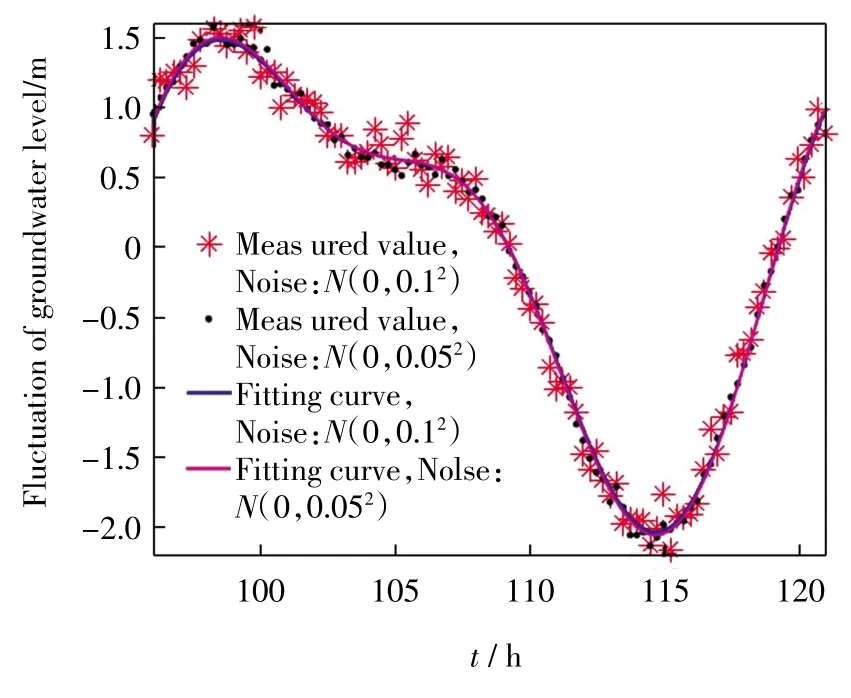
图4 仿真数据Fig.4 Synthetic data

为了识别压力传导系数D，使用Mathematica 软件的内部函数Findfit 计算误差函数最小化时的滞后时间和压力传导系数D.Findfit 的默认值为线性最小二乘的Singular value decomposition 和非线性最小二乘的Levenberg-Marquardt[17].FindFit 在内部建立了一个残差函数和雅克比，进而用于高斯-牛顿法以寻找平方和的最小值或非线性最小二乘拟合[18].

在具体计算过程中，首先，给出初始值Δt=1.555 h，D=19 000 m2/h，第 1 种高斯白噪声 N（0，0.12）条件下，识别结果为 Δt=-0.017 h，D=19 410 m2/h；第 2 种高斯白噪声 N（0，0.052）条件下，识别结果为 Δt=-0.001 h，D=20 175 m2/h.2 种噪声的滞后时间分别为0.017 h和-0.001 h，压力传导系数D 分别为19 410 m2/h 和20 176 m2/h，具体误差如表3 所示.

表3 压力传导系数的误差Tab.3 Errors in hydraulic diffusivity

在实际工程应用中，压力传导系数的误差应该低于 5%，本研究加入高斯白噪声 N（0，0.12）和 N（0，0.052）后，所得结果的相对误差分别为2.949%和0.878%，均小于3%，符合工程误差标准，充分证明运用本研究方法识别压力传导系数D 是可行的.

2.3 潮汐振幅在含水层中的衰减

潮汐信号在含水层中传播时，随着传播距离的增加，振幅逐渐衰减，且压力传导系数越大，衰减速度越小，潮汐信号传播得越远.因此，在实际操作中，需要依据含水层的透水特性确定地下水水位观测井的位置.如果观测井的位置超出潮汐信号所能到达的距离范围，则观测不到地下水水位对潮汐的响应.为此，有必要研究潮汐信号在不同压力传导系数的含水层中的衰减过程及其传播距离，为野外观测井定位提供依据.

为了比较精确地确定压力传导系数，地下水水位对潮汐的响应不宜过小.基于实际情况，本研究设定观测井位置处的地下水水位波动不得小于潮汐振幅的0.1 倍.即针对不同压力传导系数的含水层，计算地下水水位衰减至潮汐振幅的0.1 倍时的x 值.根据表2中的参数带入解析解式（5）得到潮汐最大振幅为Am=3.198 m，在含水层压力传导系数为4 000～200 000 m2/h的范围内选取具有代表性的12 个数值，得到其衰减曲线如图5 所示.由图5 可知，压力传导系数D 越大，衰减距离x 越大，不同传导系数情况下，潮汐信号衰减至0.1 Am时的衰减距离如表4 所示.

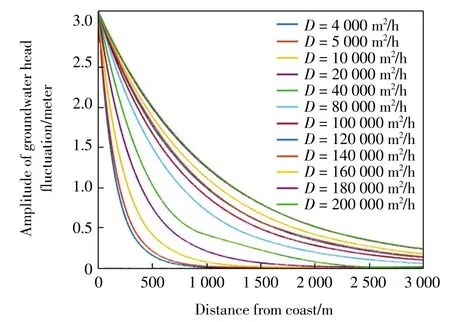
图5 潮汐振幅信号在不同压力传导系数含水层中传播时的衰减曲线Fig.5 Attenuation decaying of tide amplitude in aquifers with different hydraulic diffusivity

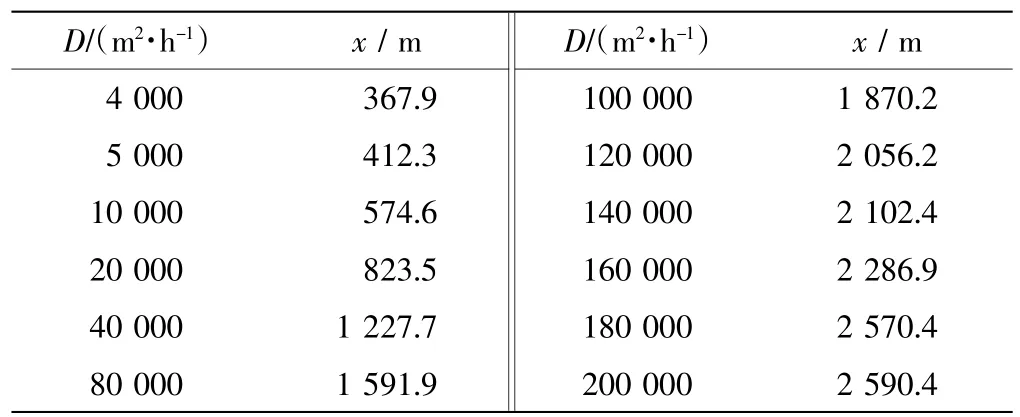
表4 在不同的压力传导系数D 的条件下地下水水位振幅衰减到0.1 Am 的距离Tab.4 Distance of groundwater amplitude decaying to 0.1 Am under different hydraulic diffusivity D

根据实际情况，压力传导系数D 的最大值约为2×105m2/h.由表 4 可以看出，当 D=2×105m2/h 时，振幅衰减到0.1 Am时x 值为2 590.4 m，不同的压力传导系数对应的x 值不同.在实际应用中，为了得到更准确的数据，应依据表4 中提供的位置钻取观测井.

3 讨论

本研究利用数值模拟的方法基于地下水水位对潮汐响应的解析解得到相关结果，而实际问题更为复杂，本研究尚存在诸多未考虑因素，如海滩是有斜坡的，含水层底部与水平方向也往往存在一定倾斜角，但本研究模型中假设海滩和含水层均为水平，且一般非承压含水层可能通过渗漏影响地下蓄水层的潮汐涨落，即实际问题中可能还含有渗漏项.这些因素都会影响地下水对潮汐的响应，也会影响在含水层中振幅的衰减.假设海滩斜坡为β，含水层底部与水平方向夹角为 θ，则当 β=90°，θ=0°时，就退化成为本研究中模型.后续工作可以考虑渗漏和斜坡混合问题，建立新的模型，用该方法来识别压力传导系数D，且可以讨论不同的D 与振幅衰减的关系，从而更好地确定打井位置.

4 结论

本研究建立了滨海地区地下水水位对多频潮汐的响应模型，将模型扩展到复数域，并结合解的叠加原理求得解析解，模拟了地下水水位对潮汐的响应过程，并在此基础上，通过数值实验采用最小二乘法识别了含水层的压力传导系数，得到以下结论：

（1）由海水潮汐引起的地下水水位波动可以作为天然的抽水试验确定含水层水力传导系数.

（2）通过数值仿真，采用最小二乘拟合函数，借助Mathematica 软件识别出压力传导系数D 和滞后时间，相对误差小于3%，满足工程地质要求，也说明该方法可以准确识别压力传导系数D.

（3）对压力传导系数D 和距离x 进行敏感性分析，把0.1 倍最大振幅作为一个标准，一般打井位置应小于振幅衰减至0.1 倍时对应的x.

（4）本研究具有一定的局限性，如没有考虑实际问题中普遍存在渗漏和斜坡，但对研究有渗漏和斜坡的问题具有参考价值.