WRF模式气象要素模拟精度的验证及订正——以南疆区域为例

宋 倩，毛 健，马振兴，陈 莉

（天津师范大学地理与环境科学学院，天津 300387）

随着中国城市化进程的加快，环境污染日益严重，导致雾霾现象时有发生，因此，对雾霾的精确预报成为当前研究的热点.而雾霾现象的产生与气象场密切相关，因此气象场预测的准确性非常重要[1].对气象数据的预测方法主要有经验预报、统计预报和数值模式预报.其中数值模式预报具有不受观测数据限制的优点，成为目前最常用的气象预报工具.近年来，新一代的数值预报模式—WRF 模式被广泛用于气象预报.然而WRF 模式的模拟效果受地形、下垫面、分辨率、驱动场和物理过程的影响，基于单一的WRF 模式很难准确预测气象要素，特别是在地形复杂的地区，WRF 模式的模拟精度往往无法满足实际需求.因此需要对WRF 模式的模拟结果进行订正，从而得到更高精度的气象数据.

常规的订正方法多基于传统的数理统计，主要以线性回归模型的方式进行订正，如线性趋势订正、多元线性订正、逐步回归订正以及最小二乘订正等方法[2-4].而以上方法采用的模型多为全局性的回归模型，模型中的回归系数是一致的，即把不同地理位置的观测数据作为一个整体进行研究和分析，并不能准确全面地反映气象数据的空间异质性.除线性方法外，许多学者也采用非线性方法进行订正，如神经网络法[5]和时间序列分析法[6]，但这些方法仍未考虑气象数据空间分布特征的影响.由于气象数据在空间上具有空间非平稳性，造成以上两类方法无法准确、全面地反映出气象数据的真实关系以及随着空间区域变化而相应变化的规律，而地理加权回归（geographic weighted regression，GWR）方法很好地弥补了这一不足.

相比常用的气象订正模型，GWR 最大的特点是考虑了空间异质性，近几年，该方法在不同学科均有所发展和应用.Zhang 等[7]通过建立GWR 模型对树冠高度问题进行分析，并通过与一般线性回归模型相比，证明GWR 模型的模拟更为科学，误差更小.Brunsdon等[8]发现与一般模型相比，GWR 模型对空间异质性具有更精确的表示.Majid 等[9]利用普通最小二乘（OLS）回归和地理加权回归（GWR）建立盐度模型，GWR 模型比OLS 回归模型具有更强的盐度预测能力，更好地反映了其空间异质性.基于前人研究，GWR 模型同样适合分析气象因子与其影响因子间的空间关系，但目前利用GWR 模型订正WRF 预报数据的研究很少见诸报道.因此，本研究以2016 年南疆地区为例，选取最优参数化方案进行WRF 数值预报，并利用地理加权回归模型订正WRF 模式的预报结果，以期获得精度更高的模拟气象数据.

1 资料与方法

1.1 实验设计与研究区介绍

南疆地区处于天山以南，昆仑山以北，光照时间长，热量充足，全年降水量少，气候干燥，年降水量仅20～100 mm，昼夜温差大，年平均气温 10 ℃～13 ℃.气候类型为温带大陆性气候，适合研究中尺度模式在复杂地形地区模拟性能的差异.为了评价地理加权回归模型的订正效果，本研究选择2016 年南疆地区23 个气象站的实测气象数据作为参考数据，气象站点分布情况如图1 所示.

1.2 WRF模式设置

本研究使用美国NCAR 等联合开发的中尺度天气研究与预报模式Weather Research and Forecasting Model（WRFv3.8）.采用三层嵌套方式，以坐标（38.8°N，83.4°E）为模式投影中心，网格数分别设置为67 ×40、115 ×67 和172 ×106，对应水平网格的分辨率设置为90、30 和 10 km，垂直分为 30 层.模式起始日期为当日12 ∶00 至次日12 ∶00.通过前期实验对比以及参考相关文献[10]，微物理参数化方案采用WSM 3 Class simpleice 方案，边界层参数化方案采用YSU 方案，积云参数化方案采用Grell-Devenyi ensemble 方案，大气辐射方案采用RRTM（长波）/Dudhia（短波）方案.

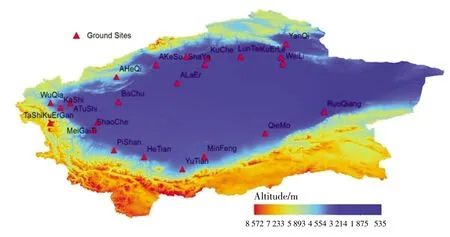
图1 新疆南缘地区气象站分布情况Fig.1 Distribution of meteorological stations in southern margin of Xinjiang，China

模式选用1°×1°的NCEP（national centers for environmental prediction，NCEP）再 分 析 资 料（final analyses，FNL）作为初始场和边界条件，模拟了2016 全年南疆地区的气象数据.WRF 模式输出每小时的温度、相对湿度和风速模拟数据，考虑到实测气象参数的分辨率，取 10 m 高度处的纬向风（U10）和经向风（V10）以及2 m 处的温度（TK2）和相对湿度（RH）作为精度评价的对象.

1.3 地理加权回归方法

地理加权回归模型（GWR）通过考虑参数的局部特征，在回归参数中考虑空间位置，并通过空间权重矩阵表示空间非平稳性，使得变量间空间位置关系更接近真实情况，模型模拟结果更科学、客观[9].GWR模型表达式为

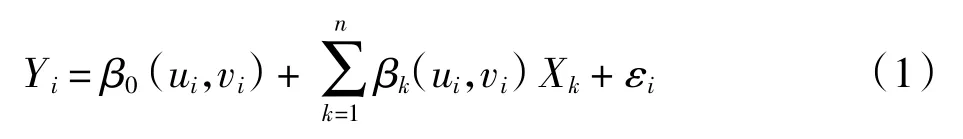
式（1）中：Yi为因变量；（ui，vi）为空间样本的坐标；k 为样本数量；Xk为第 k 个变量的值；β0为截距；βk为第 k个变量的回归参数；εi为模型残差.

空间权函数的确定极为重要，它通过空间采样点距离的远近表征权重大小，作为数据重要关系的代表，空间权函数主要包括距离阈值法、距离反比法和Gauss 函数法3 种，本研究参考文献[8]选取 Gauss 函数法作为空间权函数.在GWR 模型参数估计中还有一个重要工作是对空间核函数和核带宽进行估计，常见的空间核函数有固定型空间核和调整型空间核.与调整型核函数相比，固定型核函数克服了距离阈值与距离呈反比的缺点，适用性更强，因此，本研究选用固定型核函数，其空间权重采用高斯函数法.而确定带宽常用的方法有赤池信息量准则（akaike information criterion，AIC）法和交叉验证（cross validation，CV）法，与CV 法相比，AIC 法考虑了不同模型不同自由度的差异，更为精确，因此本研究选用AIC 法确定模型宽带.

1.4 统计分析方法

本研究选用偏差Bias、相关系数R、均方根误差RMSE 和相对均方根误差rRMSE 表征气象要素模拟的精确性.

式（2）～式（5）中：Si为 WRF 模拟值或订正后数据；Oi为气象站数据；n 为站点数目.

2 WRF模拟数据精度验证

为了验证WRF 模拟数据的精度，以实测气象参数为参考值，分别统计了WRF 模拟温度（T）、相对湿度（RH）和风速（WS）的 RMSE 值以及相关系数，结果如图2 所示.由图2 可以看出，WRF 拟合所得温度相关系数 R 为 0.95～0.99，RMSE 为 2.0～3.5 ℃；相对湿度的相关系数R 为0.45～0.80，RMSE 为11%～21%；风速的相关系数 R 为 0～0.3，RMSE 为 1.5～4.0 m/s.目前，针对该地区及附近地区的研究中，WRF 模拟的温度、湿度和风速拟合的相关系数R 分别为0.64～0.96、0.55～0.73 和 0.11～0.64；RMSE 分别为 2～7℃、18%和 1.1～4.8 m/s[11-21].本研究WRF 模拟所得温度、湿度和风速的相关系数R 及RMSE 均与上述范围较为接近，表明WRF 在本研究区整体上与已有文献结果一致[11-21]，即WRF 模拟温度的精度较好，相对湿度次之，风速最差.

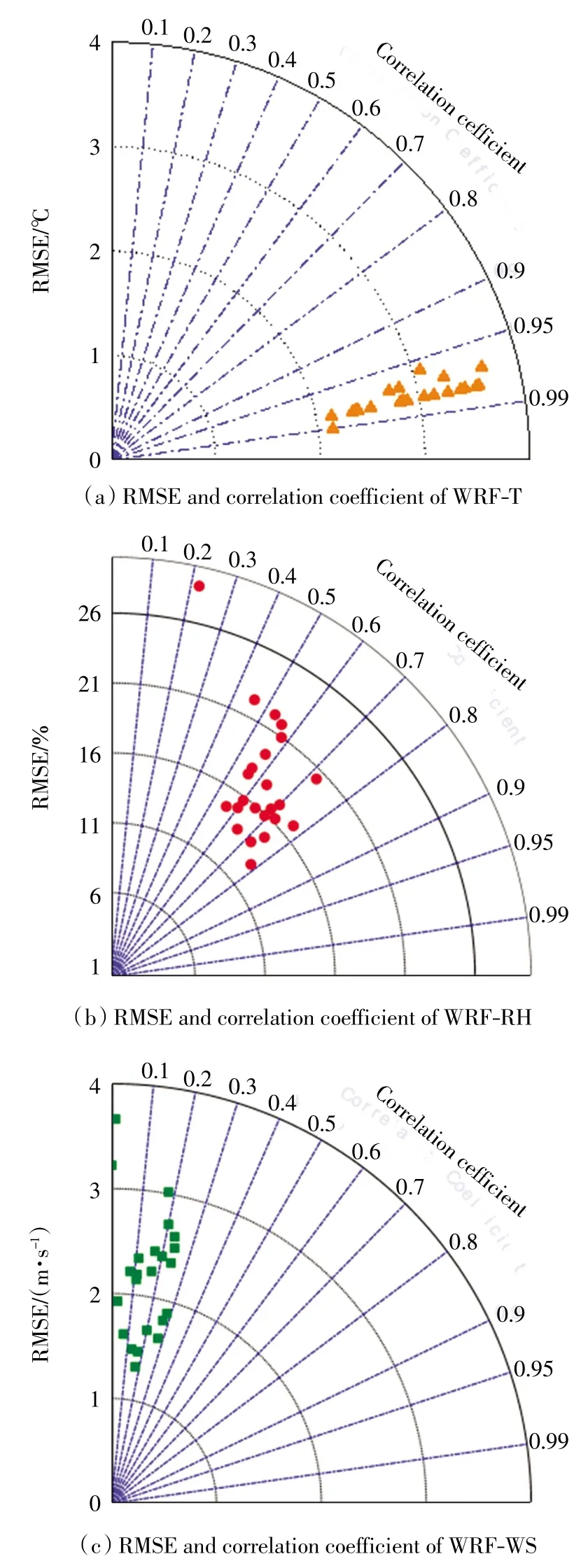
图2 WRF 模拟气象要素的泰勒分布情况Fig.2 Taylor distribution of simulated meteorological elements from WRF

考虑到南疆地区地形的复杂性以及风速与地形的密切关系，本研究进一步分析了WRF 模拟误差与地形的关系.为了直观表征不同地形下WRF 的模拟效果，图3 给出每个测站3 个气象要素的WRF 数据与气象站数据的差.

图3 WRF 模拟温度、风速以及相对温度偏差的空间分布Fig.3 Bias spatial distribution of temperature，wind speed and relative humidity from WRF

由图3 可以看出，温度、风速和相对湿度的偏差随地形的变化而变化，存在明显的空间异质性.由图3（a）可以看到，大部分站点温度差小于2 ℃，在高海拔站点偏差较大，尤其是塔什库尔干站，温度偏差最高，达到-15.3 ℃.由图3（b）可知，大部分站点风速差大于1.5 m/s，在高海拔地区偏差较大且所有偏差均为正值，说明WRF 对于风速的模拟可能存在系统性偏差，高估了气象站的风速.由图3（c）可知，大部分站点相对湿度差小于15%，同样在高海拔地区偏差较大，其中塔什库尔干的偏差最大，达到-17.1%，偏差大多数为负值，说明WRF 模式低估了气象站的相对湿度.而造成上述系统性误差的原因可能是WRF 模式在模拟大气运动时对地形进行了平滑处理，忽略了地形对模拟的影响[19].

为了定量表达地形高度与WRF 模拟精度的关系，本研究统计分析了地形高度与温度、相对湿度以及风速偏差（Bias）的相关系数，其值分别为0.82、0.83和0.54，可见地形高度与WRF 模拟精度密切相关.这也进一步说明地形高度对WRF 的模拟精度具有较大影响，在订正时必须予以考虑.

3 GWR模型订正效果分析

基于上述分析结果，采用GWR 对WRF 模式预测值进行订正时，选用高程作为自变量之一，式（1）则变为

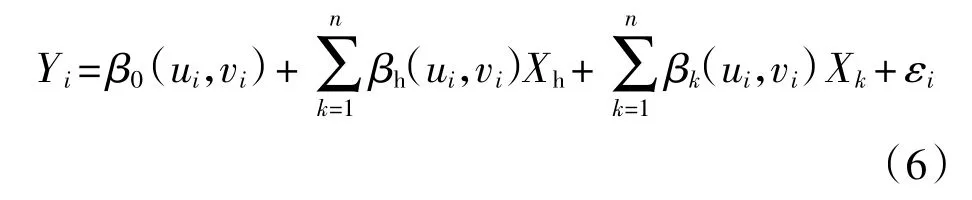
式（6）中：βh（ui，vi）是第i 个气象站的高程的回归参数，即模型函数在（ui，vi）处的权重；Xh为 WRF 高程数据Xh在第i 个气象站的值，其他值与式（1）定义相同.

利用式（6）进行订正后，采用交叉验证法验证预测精度，即将气象站数据随机均匀地分为23 组，其中1 个气象站数据留作测试集，剩余22 个气象站数据作为训练集，交叉验证重复23 次，保证每个气象站数据均被验证.表1 为订正前后预测值与实测值间的误差统计.由表1 可以看出，经GWR 订正后，温度、相对湿度以及风速无论是全年还是4 个季节，其偏差Bias 绝对值和均方根误差RMSE 值均小于订正前结果.而从季节上看，冬季温度的rRMSE 值降低最多，说明在冬季改进效果最明显，这主要是由于冬季实际温度较低导致rRMSE 偏大；相对湿度的rRMSE 值在夏季降低最多，说明在夏季改进效果最明显；同样风速的rRMSE在夏季降低最多，说明夏季改进效果最为明显，这可能主要是由于夏季水汽含量大且变化剧烈，使得WRF难以对相对湿度和风速进行精确预测.

为检验WRF 对不同风速的预报能力，以模拟风速与观测风速的比值随观测风速的分布落在2 倍线内数据的比例（FAC2），用以衡量模式的模拟能力，结果如图4 所示.图4（a）给出订正前FAC2 随观测风速的变化，当风速小于5 m/s 时，FAC2 随着风速增大近似线性增长.对于5 m/s 以上的风速，FAC2 趋于稳定，大部分都在50%以上；对2 m/s 以下风速，WRF 模拟能力较差，FAC2 低于30%；对于1 m/s 以下的风速，FAC2 降至10%，这说明WRF 对低风速的模拟能力还有待提高.张碧辉等[13]通过比较WRF 中MYJ 方案和YSU 方案，得到风速大于5 m/s 时的FAC2 约为90%，高于本研究结果，即本研究模拟风速偏差更大，这可能是因为空间分辨率不同，文献[18]中分辨率为2 km，而本文的空间分辨率为10 km，导致在地形数据精度上存在差异.图4（b）给出GWR 订正后FAC2 随观测风速的变化，当风速小于5 m/s 时，FAC2 随风速增大，近似线性增长，对于5 m/s 以上风速，FAC2 趋于稳定，大部分在80%以上，明显高于订正前FAC2 的值，说明GWR 订正后，模拟和观测风速比值落在2 倍线内数据的比例明显提高，数据与气象站数据更为接近，拟合效果更好.

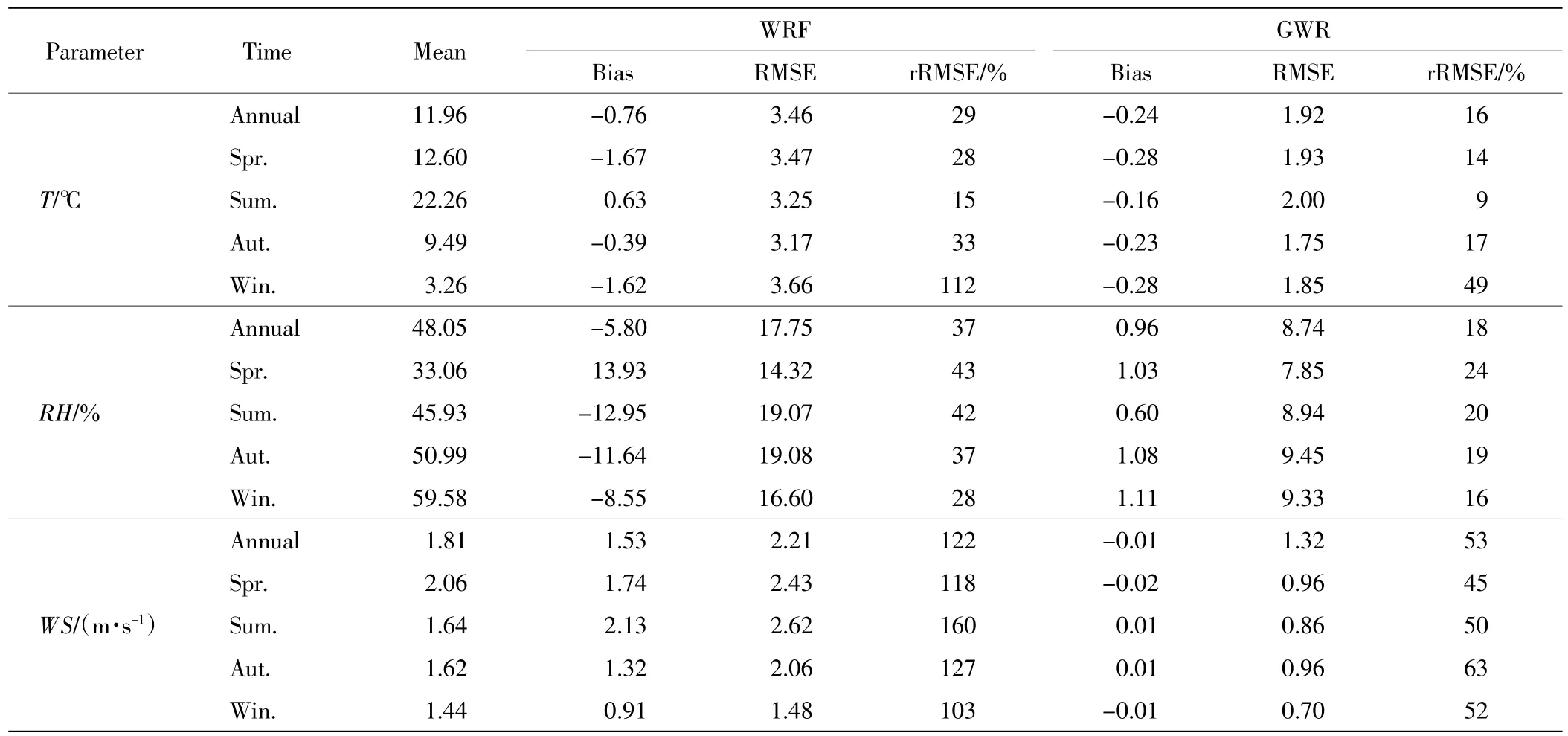
表1 GWR 订正四季平均RMSE 与rRMSETab.1 GWR revised quarterly average RMSE and rRMSE

图4 WRF 风速FAC2 随观测风速分布图Fig.4 Distribution of WRF wind velocity FAC2 with observed wind velocity

为了进一步证明GWR 订正方法的优越性，将本研究结果与已有文献中采用的其他订正方法进行比较.余江[15]通过New AR 模型对WRF 风速进行订正，订正后RMSE 改进率为15%，而本研究风速改进率为40%.黄凤新等[16]运用改进的BP 神经网络对WRF 模式模拟风速数据进行订正，rRMSE 改进率为39%，叶小岭等[17]通过PSO-LSSVM 方法对WRF 模式模拟风速结果进行订正，rRMSE 改进率为20%，本研究rRMSE改进率为57%.郑亦佳等[18]通过地形订正方法对WRF模拟冬季气温和风速进行订正，偏差改进率分别为5%和58%，本研究冬季气温和风速偏差改进率分别为83%和98%.通过上述比较可以看到，本研究GWR订正的偏差改进率、RMSE 改进率以及rRMSE 改进率总体优于其他订正方法.

通过上述对比可以看到，GWR 订正后精度总体上较高，误差也得到进一步降低，这主要是因为GWR方法通过局部回归参数描述了气象站高程与气象要素间的空间变化关系，即充分考虑了气象数据的空间异质性，可以较好地对WRF 数据进行订正.

为了进一步验证GWR 模型顾及空间异质性这一优势，对不同地形下订正前后的效果进行对比分析，表2 为订正前后每个测站3 个气象要素的rRMSE 值.

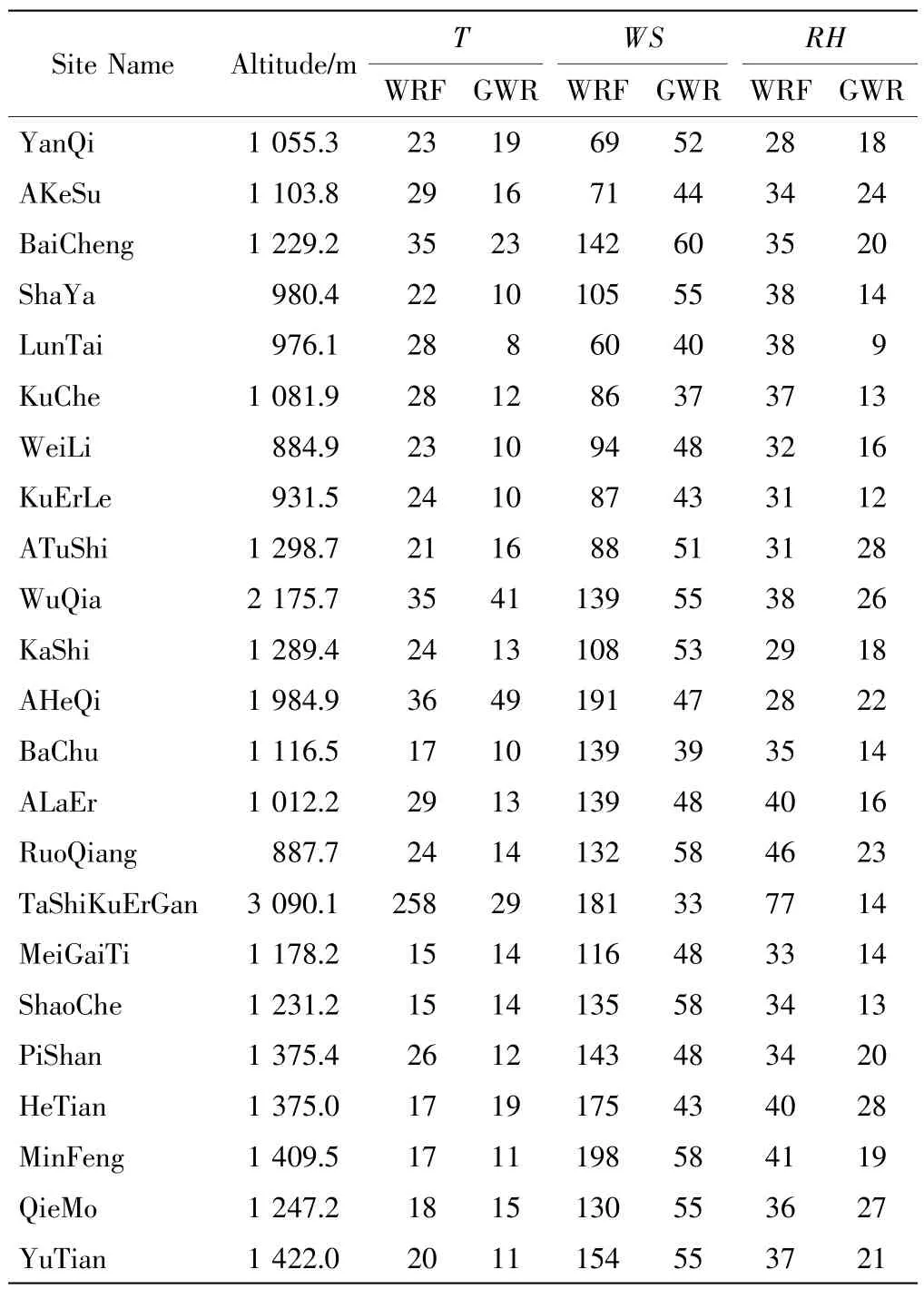
表2 GWR 订正前后温度、风速以及相对湿度rRMSE 值的比较Tab.2 Comparison of rRMSE of T，WS and RH before and after GWR correction %

由表2 可以看出，无论是温度、风速还是相对湿度，其订正后的rRMSE 值均小于订正前，而且呈现站点高程越高改进幅度越大的特点，特别是在高程最高的塔什库尔干站点，其温度、风速和相对湿度的精度分别提高229%、148%和63%，是各个站点中精度提升幅度最大的，这说明GWR 模型在顾及地形的影响后，订正效果改正明显.同样，对GWR 订正后数据的偏差值与气象站高程进行了相关性分析，得到温度、相对湿度以及风速的相关系数分别为0.45、0.14 和0.08，对比订正前的0.82、0.83 和0.54，相关性明显降低.

4 结论

本研究以南疆区域23 个气象站2016 年的实测气象数据和同时刻WRF 模式的模拟数据作为实验资料，利用GWR 对WRF 模式预报的气象数据进行订正，并验证了该模型在气象要素订正上的有效性，得到以下结果：

（1）对比WRF 模式预测结果与实际气象站的数据发现，温度和相对湿度的模拟效果较好，对小风区风速模拟效果较差，即5 m/s 以下风速的模拟较差，模拟风速偏高，低估了低风速出现的频率，高估了高风速出现的频率，这说明由于地形、分辨率、下垫面和大气物理过程等原因，WRF 模式预测结果和实际数据间存在差异.

（2）使用GWR 订正后，WRF 模式预测的气象数据与实际气象数据更加接近，误差指标RMSE 和rRMSE 均有所下降.温度、湿度和风速的均方根误差分别下降了1.49 ℃、9.01%和0.89 m/s.温度、湿度和风速的相对均方根误差分别下降了12.88%、18.75%和69.54%.与未经订正的WRF 数据对比分析后可知，GWR 订正后数据更趋近于实测数据，精度明显提高.

使用WRF 模式进行预测时，误差较大.通过引进GWR 方法进行订正后，可以有效减小预测的误差.如果在订正的过程中，考虑气压和下垫面等要素，订正效果可能会更好，本研究在时间尺度上仅利用了2016年全年的数据建立模型，今后需利用更长时间序列数据进行实验，这也是下一步研究的内容.