探究三角形四等分线分割面积的问题

黄锦涛 谢涛 叶济宇

摘要：本文对三角形边的四等分线进行研究，把分割形成的30个图形进行分类，得出各类图形的面积大小并且对图形的面积进行了证明，

关键词：三角形;四等分线;分割面积

文献[1]对三角形三等分点有关的面积问题进行了研究，并对分割以后的19块图形进行了面积的计算，把面积相同、形状相同的图形归为一类，最后给出了面积的证明，文献[2]通过引理对文献[1]的结论给出了几种不同的证明，笔者由此受到启发，并对三角形边的四等分线分割面积问题进行探究。

1问题重述

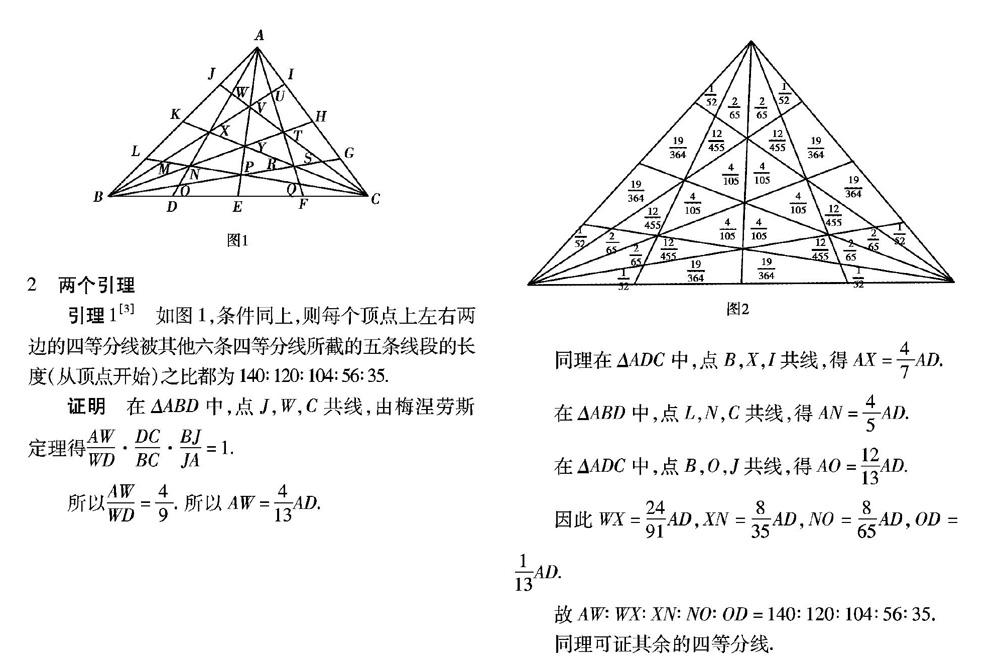
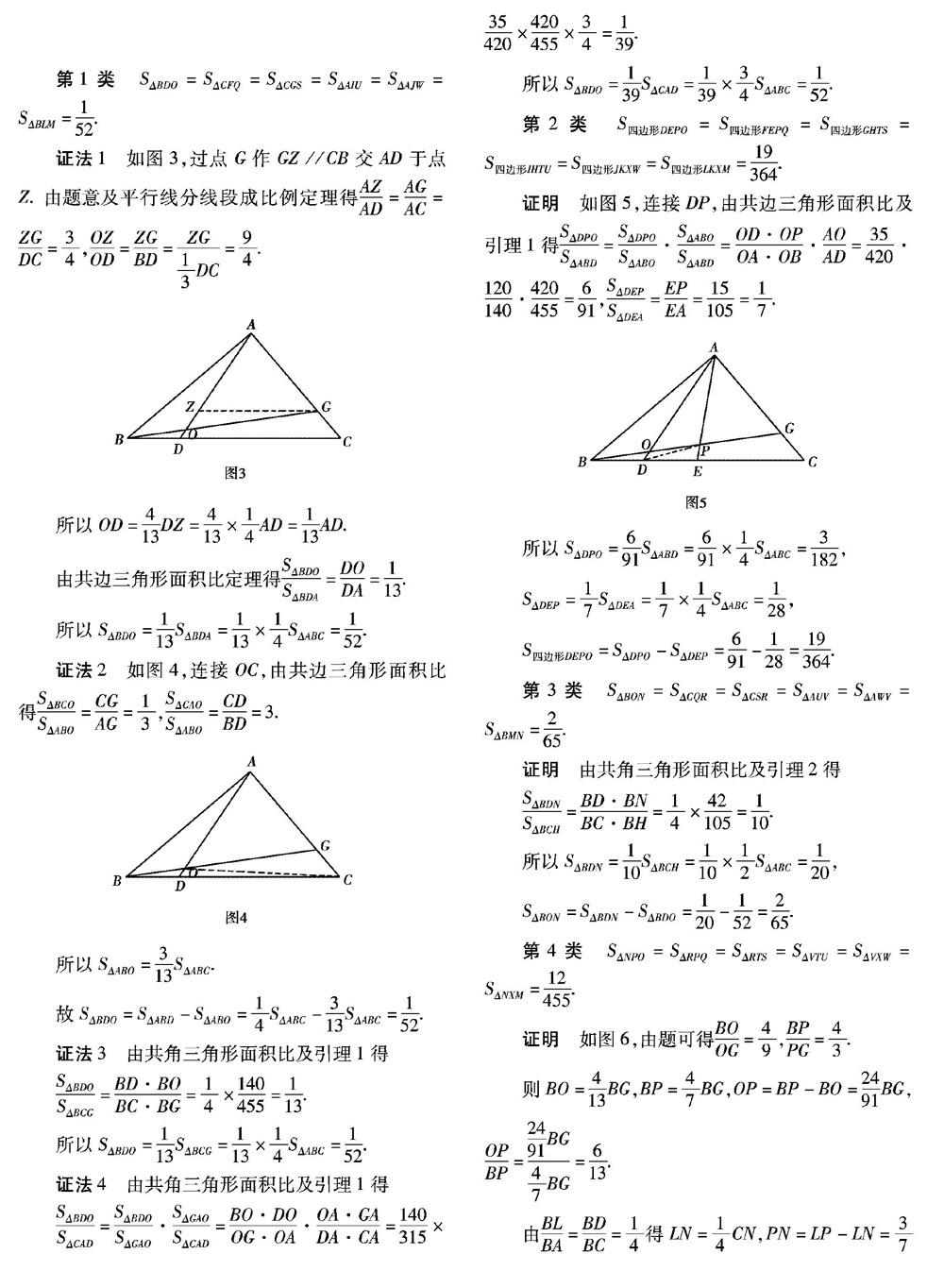
如图1所示，点D，E，F，G，H，I，J，K，L為△ABC的边BC，CA，AB的四等分点，连接AABC的顶点与对应的四等分点，把AABC分成24个三角形、6个四边形共30个图形，假设AABC的面积为1.则这30个图形的面积如图2所示。

引理2如图1.条件同上，则每个顶点上中间这条四等分线被其他六条四等分线所截的四条线段的长度（从顶点开始）之比都为42：28：20：15.

证法与引理1类似。

3面积问题的证明

通过对图2的观察可以发现，这30个多边形可以分为以下六类，下面给出这六类面积的证明，为节省篇幅，下面只证各类结论中的第一个面积，其余同理可得，同时从第2类面积起，只列举出一种证法，其余证法可参照第一类面积的证明。