某地铁车站基坑围护结构变形过大的实测与计算分析

苏卜坤，姜燕，孙树楷，刘清华

（1、广州市市政工程设计研究总院有限公司广州510060；2、广东省水利水电科学研究院广州510610；3、广东省岩土工程技术研究中心广州510641；4、华南理工大学广州510640）

0 引言

目前，随着地铁在各大城市的快速发展，出现各种问题的概率也不断增大。特别是在广州这种地质条件复杂、建筑物密集的地区兴建地铁，需要处理许多特殊的技术问题。现在广州地铁最常见的围护结构形式之一就是地下连续墙+首道混凝土支撑（往下钢支撑）的形式。在车站运营阶段，地下连续墙与主体结构墙形成复合墙结构，一起作为车站外墙抵抗外侧水土压力［1，2］。

在开挖阶段，围护结构常规计算则是针对车站这种长条形基坑，假设为平面模型进行计算，除车站端部基坑空间效应明显外，这种假设有较好的适用性。同时，在第四纪土层中，采用荷载结构法，概念清楚、荷载明确，计算简单，多年实践证明是行之有效的方法［3，4］。此时，可采用商业化专业软件等进行简化计算，实用、方便、快捷。

但这种常规设计计算方法也有缺点，边界条件的设置较为固定，不够灵活。比如出现基坑变形过大、超出原设计的计算结果时，需要对其进行原因分析、施工过程（超挖、坑底软化等）模拟以及安全性评价时，常规计算软件及方法则显得有些无能为力［5］。

此时，通用有限元软件（如Civil 等）显示出其优势，可以根据施工现场情况，模拟各种边界条件和不同工况；结合实测数据，还能进行参数反演，从而修正原始输入数据。只有输入相对准确的基础参数，合理简化边界条件，这样利用软件计算出来的结果才可靠、可信。否则，软件作为一种工具，你输入错误参数，它则输出错误结果［8-14］。

对于上述问题，在当前的设计计算中还没有得到很好的解决，针对这些问题，本文以一个围护结构变形过大的地铁车站的反演复核计算为例，详细介绍了所采用的计算方法和模型［13］，并将计算结果与实测数据进行了比较，得到几点结论，以供类似工程参考。

1 工程概况

某地铁车站是广州市轨道交通新线某支线工程的中间站，位于市政干道交叉口处，沿南北向路中布置。市政道路现状均为双向六车道，基坑周边主要是在建和拟建的商业和配套项目。车站为地下2层岛式站台车站，覆土厚度约3.6 m，全长为220 m。站位所在地为丘陵台地地貌单元，地形较平坦，地形标高在43.50～44.20 m之间，南侧为剥蚀残丘；西侧地形平缓，属剥蚀残丘与丘间沟谷过渡地带。本车站范围内上覆第四系人工填土层（Q4ml）、第四系上更新统-全新统陆相冲积-洪积砂层第四系冲积-洪积土层第四系残积土层（Qel），下伏晚志留世花岗岩（S3）。

车站采用明挖顺作法施工，主体围护结构基坑标准段宽度为19.70 m，基坑深度约16.98～18.93 m；围护结构采用800 mm厚连续墙+3道内支撑的型式。连续墙嵌固深度为8.0 m，坑底主要为可塑状砂质粘性土、砾质粘性土〈5H-1〉和硬塑状残积砂质粘性土、砾质粘性土〈5H-2〉层。典型断面如图1所示。

图1 车站结构横断面Fig.1 Cross Section of Station Structure

基坑于2014 年12 月20 日开始第1 层土方开挖，在开挖至9轴以前，挖到基坑底时的连续墙测斜、地面沉降等均在正常范围，未超出警戒值。

2015 年6 月22 日开挖至9 轴时出现险情。开挖至深度9.5 m 时，墙体测斜点B04 处累积达到报警值35 mm；6月22日晚22时，开挖至深度11.5 m处时变形达到控制值，累积位移42.3 mm。完成第2道钢支撑安装后（开挖至深度约13.7 m），开始开挖第4层土方，基坑变形持续加大，最大水平位移增加至50 mm。现场为安全起见，采取了在基底垫层顶面以上1.7 m位置安装第3道钢支撑措施后，到7月5日墙体稳定，监测无明显变化，墙体在深度15.5 m处累积位移为52.9 mm。

后续一段的车站基坑开挖时加强施工控制，严格按照设计要求进行，墙体测斜均还是产生了较大变形，最大值也达到了约48 mm。

2 数值模拟方法介绍

对于上述工程出现的问题，需要立即查找原因，以便计算分析现有连续墙承载力是否足够，安全储备如何等。具体计算方法及过程如下：

2.1 计算参数

初始计算参数的选取主要依据地勘报告确定。主要地层为人工填土〈1〉、淤泥〈4-2A〉、淤泥质土〈4-2B〉、可塑状砂质粘性土、砾质粘性土〈5H-1〉和硬塑状残积砂质粘性土、砾质粘性土〈5H-2〉层，全、强风化花岗岩层。各岩土层及材料参数如表1所示。

表1 岩土物理力学参数值Tab.1 Physical and Mechanical Parameters of Rock and Soil

2.2 计算模型

模型假设如下：

⑴ 模型沿车站纵向取1 m，将车站视为弹性地基上的平面框架结构进行计算；

⑵ 明挖顺做时，开挖阶段不用考虑围护结构与主体结构的共同作用，当采用盖挖逆作时，则要考虑围护结构与主体结构的共同作用，两者之间用只承受压力的连杆相连，当连杆受拉则自动失效；

⑶ 采用地层弹簧模拟地层反力，弹簧刚度=基床系数×分段长度。地层弹簧设置为只受压，受拉则弹簧失效。

⑷ 侧向土压力采用主动土压力，水土分算。明挖顺做一般采用主动土压力，当采用盖挖逆作法施工时，由于用刚度很大的顶板、楼板等水平构件代替临时支撑，基坑开挖过程中墙体水平位移一般较小，墙背土压力可近似按静止土压力考虑［2，3］。

计算模型及荷载分布如图2所示。本计算采用通用空间有限元分析软件MIDAS-CIVIL进行计算分析。

模拟时有以下几点需要说明：

⑴ 土弹簧沿墙背全高范围及开挖侧坑底以下均设置，即在围护结构内外侧均设置只压弹簧，采用节点弹性支承；

⑵ 对于临时钢支撑，也是采用等效刚度，在相应节点处设置节点弹性支承；

⑶ 设置施工阶段时，将开挖步与施工步分开。在开挖步，模型结构单元不变，钝化相应开挖深度范围内的地连墙内侧只压弹簧，同时施加由此开挖步产生的侧向水土压力；待变形后，激活在开挖后需施工的结构单元或约束（临时支撑、结构板等）。主要模拟步骤如图3所示。

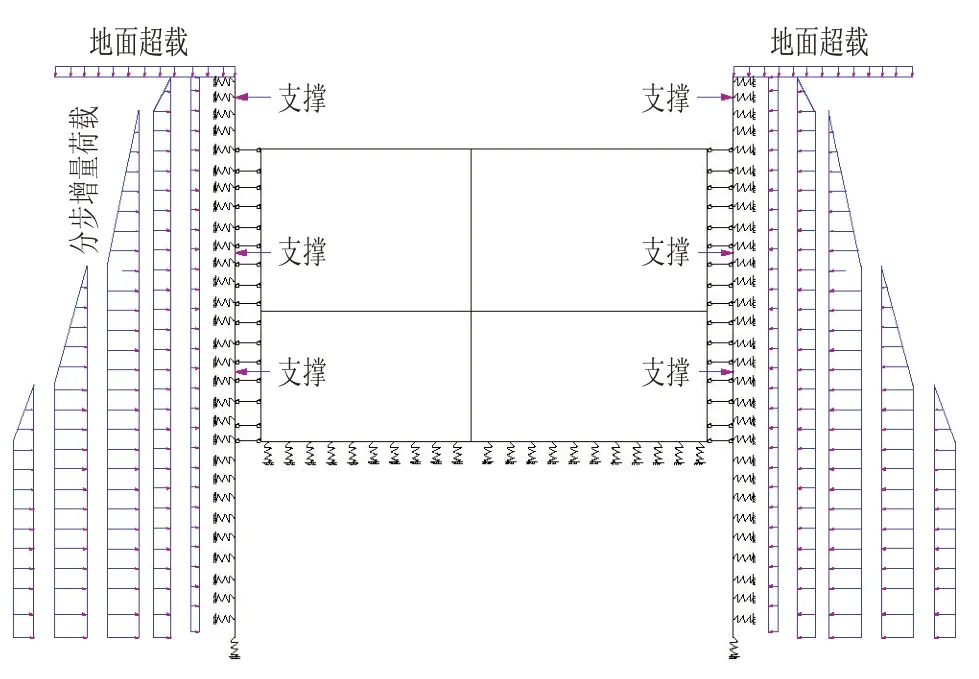
图2 车站围护模型及荷载Fig.2 Station Envelope Model and Load

图3 主要模拟步骤Fig.3 The Main Simulation Steps

2.3 根据实测数据反演计算参数

大多数地勘报告提供的基床系数Kh、Kv（含水平及垂直）也均为经验或是估计参数，为计算准确，此参数可根据实际开挖监测数据进行反分析修正（见图4、图5）。

根据现场反馈情况，车站基坑1～8 轴开挖基本正常，天气也较好，施工工序也严格按照设计步骤进行。根据该段的实测数据，结合地勘报告数据，反复试算确定各层土的基床系数如表2所示。

此时，开挖到基坑底时连续墙的计算水平位移如图6所示。

对比图4、图6可以发现，实测最大位移为24 mm；计算最大位移值22.5 mm，墙体水平位移较为一致，最大值的位置和数值也相差无几，说明基床系数取值较为接近实际数值，计算可靠。从表3可以看出，计算连续墙最大弯矩标准值为481 kN·m，各道支撑的轴力变化也较为均匀，钢支撑间距3 m，最大轴力标准值约为：677×3=2 031 kN。

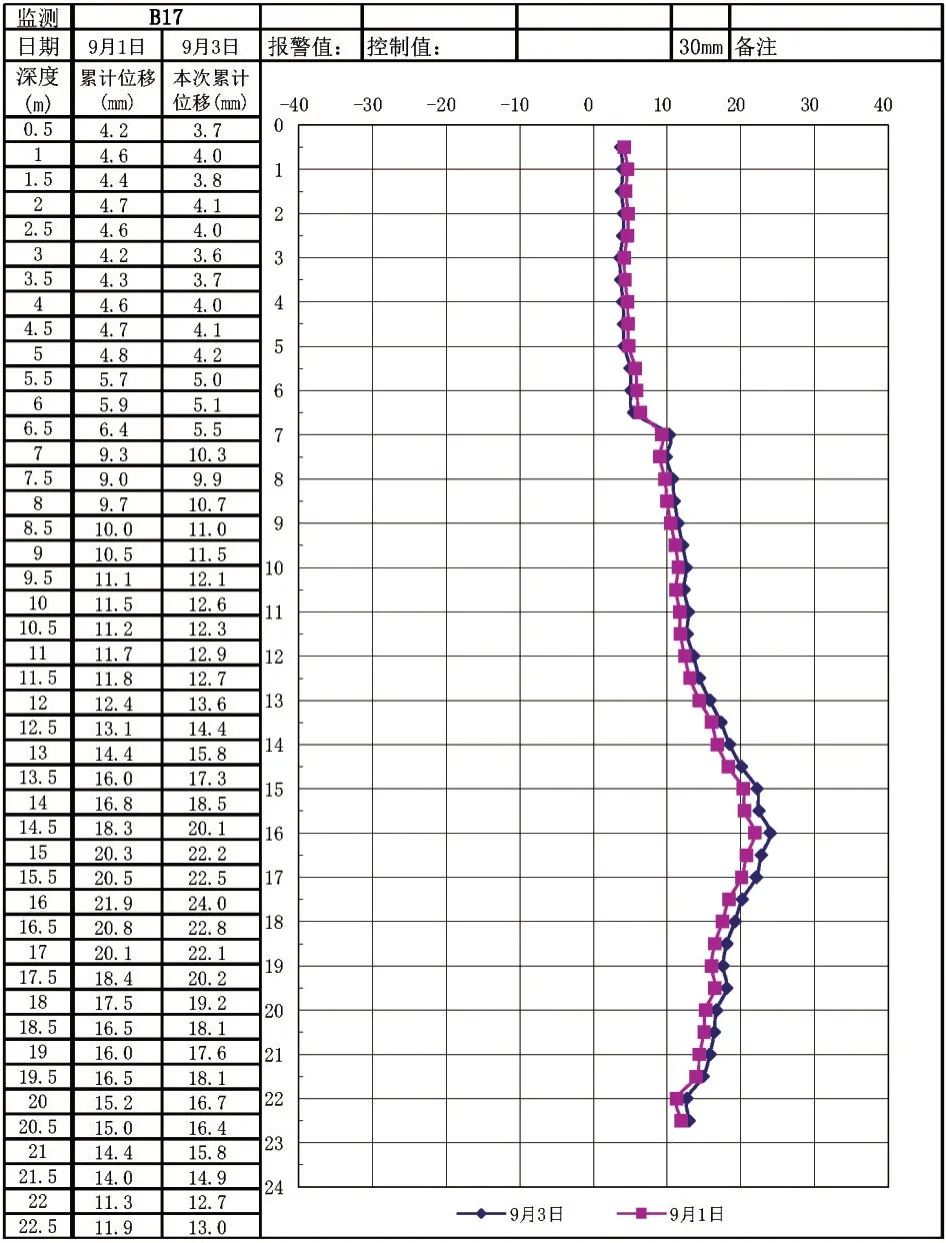
图4 开挖到基坑底实测墙体水平位移Fig.4 Horizontal Displacement of Measured Wall When Excavating to the Bottom of the Pit

表2 岩土物理力学参数反演值Tab.2 Inversion Value of Physical and Mechanical Parameters of Rock and Soil

3 围护结构变形过大工况计算

根据现场情况反馈，该地铁车站基坑施工至9 轴时，恰逢广州雨季，暴雨连连，再加上施工单位赶工期，造成第2 道支撑架设不及时，导致出现前面提到的险情，最大位移达52.9 mm。同时，发现首道混凝土支撑与冠梁节点处上表面出现裂缝，如图7红线处。

图5 基坑监测点平面布置Fig.5 Layout of the Monitoring Points of the Foundation Pit

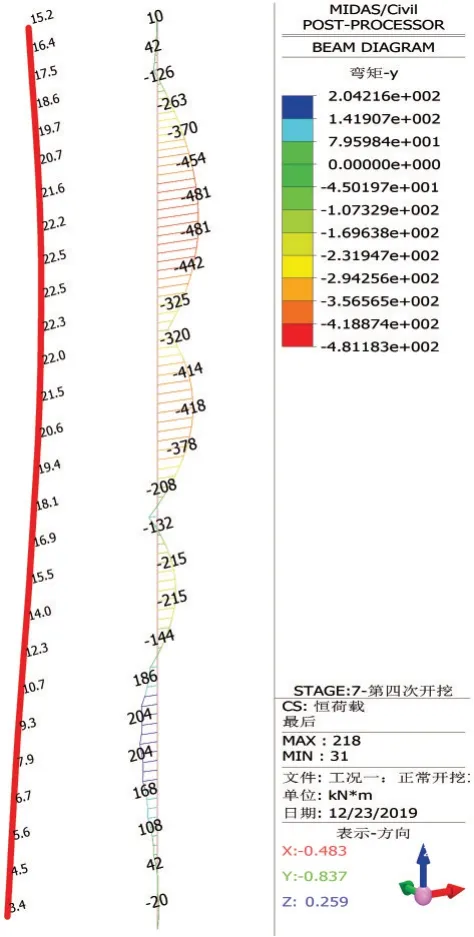
图6 开挖到基坑底计算墙体水平位移及内力Fig.6 Calculate the Horizontal Displacement and Internal Force of the Wall When Excavating to the Bottom of the Foundation Pit

表3 正常工况下支撑轴力变化情况Tab.3 Change of Supporting Axial Force under Normal Conditions

图7 报警工况时第1道混凝土支撑裂缝Fig.7 The First Concrete Supporting Crack under Alarm Condition

根据施工单位反馈的暴雨情况、支撑架设时间及开挖面长度，重新进行建模模拟计算［14］。具体施工步骤如表4所示。

表4 计算工况Tab.4 Calculation Cases

考虑软化后的土体参数的变化，进行了标贯试验，根据标贯试验击数对比及反复试算，确定软化后的地基土弹簧刚度如图8所示。

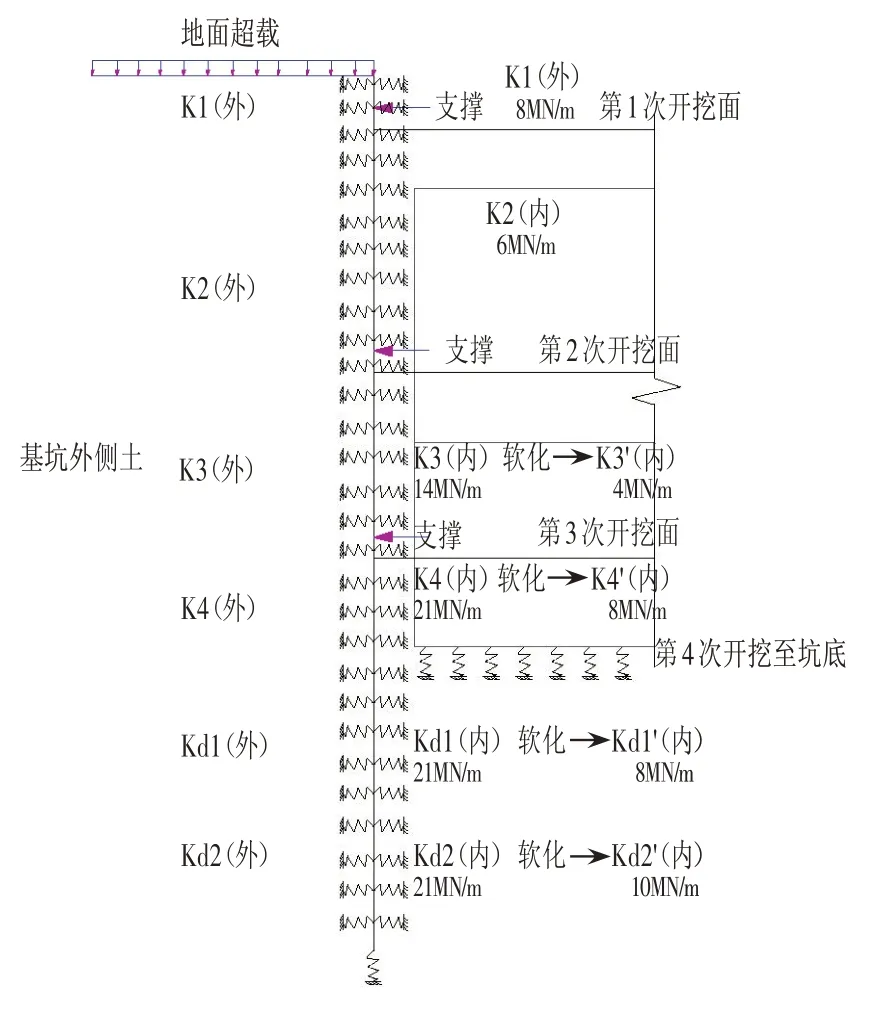
图8 基坑软化后地基参数Fig.8 Foundation Parameters after the Pit Softened

由于本文在建模时对围护结构内外侧均设置只压弹簧，来实现模拟侧向土压力在开挖过程中，随着土体挖除、支撑的架设、基坑底的土体软化等引起侧向支撑刚度变化，从而引起侧向土压力的不断变化。

从表5计算结果可以看出，计算最大位移值47.8 mm，计算连续墙最大弯矩标准值为1 012 kN·m。各道支撑的轴力变化较大，第1 道混凝土支撑间距9 m，轴力由开始的3 375 kN（375×9=3 375）增加到4 860 kN，随着第2 道钢支撑的滞后架设及坑底土的软化，第1 道混凝土支撑轴力又减小至3 600 kN。第2、3道钢支撑间距3 m，最大轴力标准值约为1 181×3=3 543 kN。

表5 报警工况支撑轴力变化情况Tab.5 Change of Supporting Axial Force under Alarm Conditions

4 结果分析

4.1 数值模拟分析结果

从图9 中可以看出，最大水平位移约为48 mm。与实际监测数据较接近，稍微偏小。其主要原因应该是侧向土压力为通过强度参数c、φ值计算的主动土压力，没有根据坑底土软化情况进行调整，比实际的土压力值偏小，但误差不大，不影响计算分析的定量判断。

图9 开挖至坑底围护结构位移、内力Fig.9 Displacement and Internal Force of the Retaining Structure When Excavating to the Bottom of the Pit

连续墙的最大弯矩标准值由正常工况的481 kN·m增大至1 012 kN·m，增加110.4%，钢支撑的最大轴力标准值由2 031 kN 增大至3 543 kN，增加74.4%，接近该钢支撑的最大承载力能力设计值3 600 kN。

4.2 常规方法验算的不足

按照前述施工过程，采用常规方法（理正深基坑软件等）计算对于这种坑底土体软化、水平及竖向支撑刚度降低的情况很难模拟，无法计算此等特殊工况下的支护结构最大位移和内力，无法判断支护结构是否已超出承载能力。

5 结论

本文对广州地铁车站某典型基坑最常见的支护方式：明挖顺做+地下连续墙+内支撑的典型支护型式基坑进行了施工全过程数值反演计算；根据现场实际情况，考虑了不同阶段的坑底软化、支撑架设不及时等，并与实测结果进行对比，较为准确地反映了内力和变形的变化情况，该方法解决了常规设计计算方法与工具很难模拟和准确计算的问题。对特殊工况（变形过大、支护结构开裂等）可以对其进行原因分析、施工过程（超挖、坑底软化等）模拟以及安全性评价。为其它类似设计提供参考。

通过计算对比分析，有以下几点值得注意：

⑴ 应按实际施工情况分阶段模拟，并根据监测反馈数据进行反演土层弹簧刚度等参数；当计算地连墙变形形状及数值与实测相符时，土层参数才可认为合理；

⑵ 利用反分析得出的土层参数计算不同工况下的内力与位移，并可对基坑施工全过程进行最大位移预测和最大内力的预测；

⑶ 在坑底软化的情况下，围护结构出现踢脚现象，混凝土支撑与连续墙连接处的上表面会出现局部拉裂缝。但是，首道混凝土支撑仍受压，同时由于与连续墙的刚接以及支撑竖向高度较大的影响，导致出现表层拉裂缝，而非首道混凝土撑受拉。

⑷ 在坑底软化的情况下，连续墙的最大弯矩点会比正常的下移，随着墙底踢脚位移的增大，弯矩越来越大，此时需要复核连续墙的极限承载力（极限弯矩、极限剪力）是否足够。

⑸ 正常施工工况下，首道混凝土轴力越来越小；在坑底软化或超挖未及时支撑的工况下，则为先增加后减小的趋势。