运用方格图提高小学图形面积教学效果的实践与思考

赖玉翠 黄勇明

【摘要】方格图是小学数学教材较为广泛应用的数学工具之一。方格图为学生提供了解决问题的“脚手架”，帮助学生更好地学习数学知识，获得数学学习的方法。本文根据“平行四边形的面积”的教学实践，浅议方格图对图形与几何板块的“图形测量”教学的积极作用。

【关键词】方格图;面积测量;教学效果

方格图是以若干小正方形为基本构成要素，以信息加工过程的直观性为形态的数学学习工具。它具有从“抽象到形象”“模糊到清晰”“粗略到精确”的作用，有助于经历“现象—本质”的知识探究过程，积累丰富的数学活动经验。如何利用方格图的直观性帮助学生理解和感受面积单位的个数和面积之间的联系，以及图形转化前后的数量关系，从而提高图形面积的教学效果呢？下面以“平行四边形的面积”教学为例，谈谈方格图的运用给我带来的几点教学体会：

一、方格图运用的缘起

1.“平行四边形的面积”教材分析及教学线索

“平行四边形的面积”是以长方形面积计算为基础，以图形内在联系为线索，以未知转化为已知的基本方法开展学习，渗透“转化思想”。在以往的“平行四边形的面积”教学中，都是先让学生通过方格图数出长方形和平行四边形的单位面积个数，并从所填写的表格数据中发现两个图形之间存在的数量关系，从而引导学生猜测、想象平行四边形面积计算公式后，用剪拼法把平行四边形转化长方形，最后让学生从操作结果中发现等量关系来验证公式的。依据以上的教材分析，我们对“平行四边形的面积”一课执行了以下的教学线索：

（1）创设“比较长方形花坛和平行四边形花坛面积大小”的情境;

（2）利用数方格的方法求面积;

（3）动手剪拼，将平行四边形转化成长方形，再求面积;

（4）观察比较平行四边形与转化后的长方形，发现等量关系，概括面积公式;

（5）综合运用平行四边形的面积公式解决问题。

2.源自教学的困惑

小学生认知水平还是以形象思维占主导，而抽象思维就比较薄弱。“平行四边形的面积”在图形转化的过程中，需要学生根据转化前后图形观察发现“底=长”“高=宽”的等量关系，但图形“边线”的抽象性导致了学生对于这一等量关系的发现存在困难，需要教师根据剪拼出来的图形一步步带着学生发现等量关系，最终，对于平行四边形面积的计算公式都要老师引领学生总结、归纳出来，而不是通过自主发现的学习方式获得知识，使课堂教学的开放性出现局限。这样的教学，老师讲得辛苦，且学生没有真正理解平行四边形转化成长方形之后存在的等量关系，真可谓“费煞苦心”。

3.基于问题解决的设想

“转化”数学思想的应用在“图形测量”是从五年级上册“平行四边形的面积”开始，对空间想象能力不强的学生来说具有一定的学习困难，而困难的本质就是因为“抽象”。要解决这个学习难点，能否为学生在推导平行四边形面积的全过程中，为学生提供一个“脚手架”，而这个“脚手架”的作用就是把抽象的知识变成直观，在直观的图形中去发现抽象的数量关系，从而为平行四边形公式的推导奠定基础。

二、数学工具的选择

解决抽象过渡到直观的思维过程，让学生通过观察直观物体来获取对平面图形的直接经验，方格图这一数学工具就有这种功能和价值所在。平行四边形的面积主要是通过对图形的剪拼、平移得到另一个等积变形的图形，从而渗透转化的数学思想。然而，在图形转化之后，基于学生对图形抽象的特征及其关系感知不深，难以抽象等量关系。利用方格图横竖线之间的垂直关系，能够凸显平行四边形和长方形的图形特征，在学生转化之后根据显性出来的图形特征，更容易发现图形之间的联系。另外，方格图能够为图形提供研究的数据，每个方格长度都能“以一当一”，直观的数据比起图形边线重合更具有可信度，从而提高图形转化实验的可信度。

三、方格图在图形测量的运用策略

（一）用好方格图的垂直作用，凸显图形的特征

小学生以形象思维为主，主要是通过观察来获得对平面图形的直观经验。在长方形、正方形面积公式推导中，方格图的主要功能定位在实现从“测量面积”到“计算面积”的过渡。而在平行四边形面积公式的推导中，方格图除了可以实现和长方形、正方形一样的功能定位，还可以把两种图形内在的数量关系质感呈现。

例如，在方格图中出示一个底是6厘米，高是4厘米的平行四边形和长是6厘米、宽是4厘米的长方形，让学生猜一猜平行四边形和长方形的面积谁大？引导学生观察平行四边形与长方形有什么不同的地方？学生在观察中发现长方形的四条边互相垂直，全都是满格的，可以用数方格的方法直接计量长方形的面积，还发现长与宽的乘积就是长方形所占面积单位的个数，从而推导出长方形面积的计算公式。但是平行四边形的四条边不是互相垂直的，造成有满格的和不满格的现象，要度量平行四边形的面积，学生就要根据平行四边形的特征想方法把不满格转化成满格的来数，为平行四边形转化成长方形打下铺垫。

（二）用好方格图的度量作用，积累图形面积的测量法

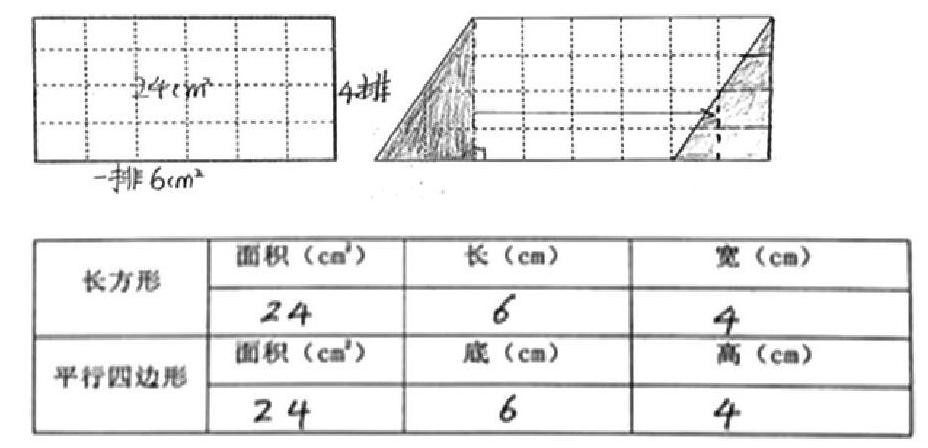
学生通过用不同的数方格的方法来计算平行四边形的面积，发现平行四边形和长方形的面积一样大，平行四边形的底和长方形的长相等，平行四邊形的高和长方形的宽相等。因为长方形的面积=长宽，那么平行四边形的面积是不是也有计算公式，从而猜想平行四边形的面积=底高。

方法一：先数整格，再通过两个不满格拼凑满格的方法。

方法二：也是用数方格的方法，把左边阴影的直角三角形格子补到右边，变成了长方形，它们的面积是以一样的，再数出长方形整格的数量就是原来平行四边形的面积。

方法三：把平行四边形沿着它的高剪下，分成了一个直角三角形和直角梯形，把直角三角形平移到直角梯形的右边，拼成了长方形，长方形的面积等于平行四边形的面积。

方法一和方法二是数格法的灵活运用，方法三是剪拼法。学生比较后发现剪拼法更简便，把面积未知的平行四边形变成学过的长方形来求，学生经历了独立思考、自主操作、合作交流的全过程，积累了单位面积测量法的活动经验，为操作验证环节奠定基础。也让学生体会到方格图的主要功能是实现从“数格法”到“剪拼法”的转化。

（三）用好方格图的直观作用，渗透数学思想方法

方格图可突显图形的特征，使各种图形之间的联系更加突出，为平面图形的转化提供了直观参照。同时，方格图还为学生直观地提供各种研究数据。根据小学生的年龄特点，平面图形面积公式推导以实验法和不完全归纳法为主，因此教师应充分提供研究数据，尽可能提高推理的可信度，从而增强学生思维的严密性。在平行四边形面积公式的验证中，老师要求学生小组合作，用大小不同，形状不同的平行四边形来验证：是不是所有的平行四边形都可以转化成长方形，它们之间都存在着以下三种等量关系？

长方形的面积=长×宽

‖       ‖    ‖

平行四边形的面积=底×高

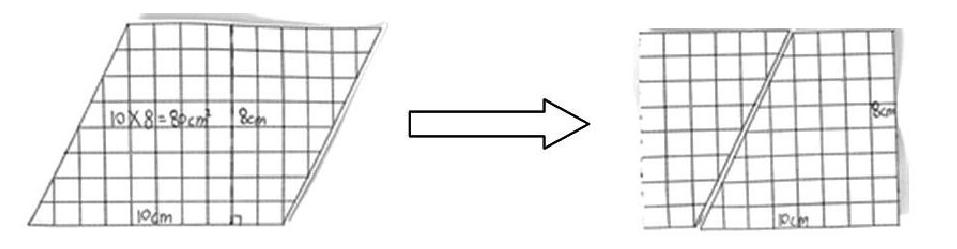
验证一：我们小组的平行四边形底是10cm，高8cm，沿着图形中间的一条高剪一个直角梯形平移到另一边拼成一个长方形，长方形的长是10cm，宽是8cm，平行四边形和长方形面积相等，底和长相等，宽和高相等。

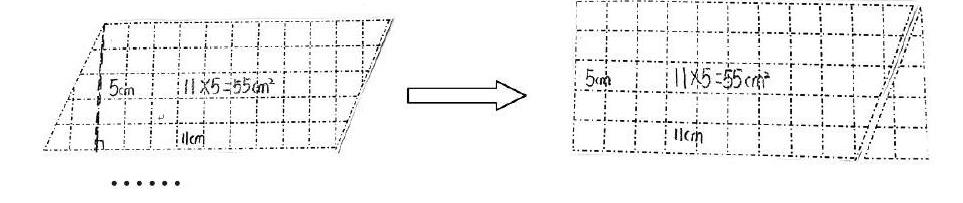
验证二：我们小组的平行四边形底是11cm，高5cm，沿着平行四边形高剪一个直角三角形平移到另一边拼成一个长方形，它们和底是6cm，高时4cm的平行四边形转化后的数量关系是一样的。

……

通过验证，学生发现任意一个平行四边形都能剪拼成一个长方形，所以“平行四边形面积=底×高”的猜想是正确的。

从方格图中抽象出转化前后图形之间的数量关系，只是一个特殊的情况，要让学生感悟平行四边形面积公式的一般性，需要通过不完全归纳的推理过程。所以教师设计了让学生运用方格图的具体数据直观性验证“转化前后”两个图形的数量关系。让学生经历特殊到一般的学习过程，学生不仅知其然，也知其所以然，从把抽象数量关系变为直观数量关系，理解了转化前后图形之间的等量关系，进一步凸显渗透“转化”“等积变形”“一一对应”的数学思想和方法。提高学生测量图形面积的思维空间，提高课堂的教学效果。

从以上的教学实践案例可知，学生在平面图形面积公式推导过程中，运用方格图让学生经历了从抽象——直观——抽象的公式推理和验证的全程。在这节课中方格图的运用，不仅激活学生使用数学工具的兴趣，还积累单位面积的测量方法，进一步学会把未知图形转化成已知图形渗透“转化”“等积变形”“一一對应”的数学思想和方法，提升学生测量图形面积的思维空间，从而推导出未知图形的面积计算公式，达到提高图形面积的教学效果。

（本文系广州市增城区教育科学“十三五”规划2019年度课题（课题编号：zc2019072）成果）