大跨度钢结构人行悬索桥受力性能对比分析
张清旭 宁晓骏 周兴林 李启萌 江小飚
(1.昆明理工大学建筑工程学院 昆明 650500; 2.云南省港航投资建设有限责任公司 昆明 650051)
0 引言
在各类桥梁结构中,悬索桥具有构造简单、造型优美、规模壮观等特点,常被称为“桥梁皇后”。目前国内大跨径悬索桥大多采用双塔三跨或单跨的形式,随着跨径的增大,主塔、主缆和锚碇的规模增加,各项拉应力和负载形式也迅速增加,工程的安全性显得尤为重要[1]。
在研究非传统悬索桥时,双缆悬索体系引起了国内外不少学者的关注,主要分析了双缆体系在承受满布均布荷载的情况下,荷载在上缆与下缆间的分配情况;研究了双主缆悬索体系在承受不平衡活载时的力学特性;推导了双主缆悬索体系对桥塔顺桥向约束的刚度表达式;分析了双缆多跨悬索体系与传统多跨悬索体系在活载作用下主缆用钢量的差异[2-5]。这些研究大多面向大跨多塔刚性悬索桥,而针对双缆体系是否适用于大跨人行悬索桥以及是否满足安全需求的研究较少。
基于此,利用有限元软件Midas/Civil对某大跨度钢结构人行悬索桥在单缆和双缆两种结构体系下静动力特性进行对比分析,总结双缆体系的力学特点,为类似的工程建设提供参考。
1 工程概况
以某人行悬索桥为背景,构建了基于单缆结构体系和双缆结构体系下的双塔悬索桥。大桥位于云南省德宏州芒市某景区内,主跨188 m,桥梁全长287 m,矢高12.533 m,矢跨比为1/15。桥宽3 m,桥面净宽2 m,桥面为钢化夹层玻璃。双缆体系下顶缆矢高11.753 m,矢跨比为1/16,底缆矢高13.431 m,矢跨比为1/14。桥梁立面位于半径为9 400 m的圆曲线上,立面布置如图1。

(a) 单缆悬索桥 单位:m
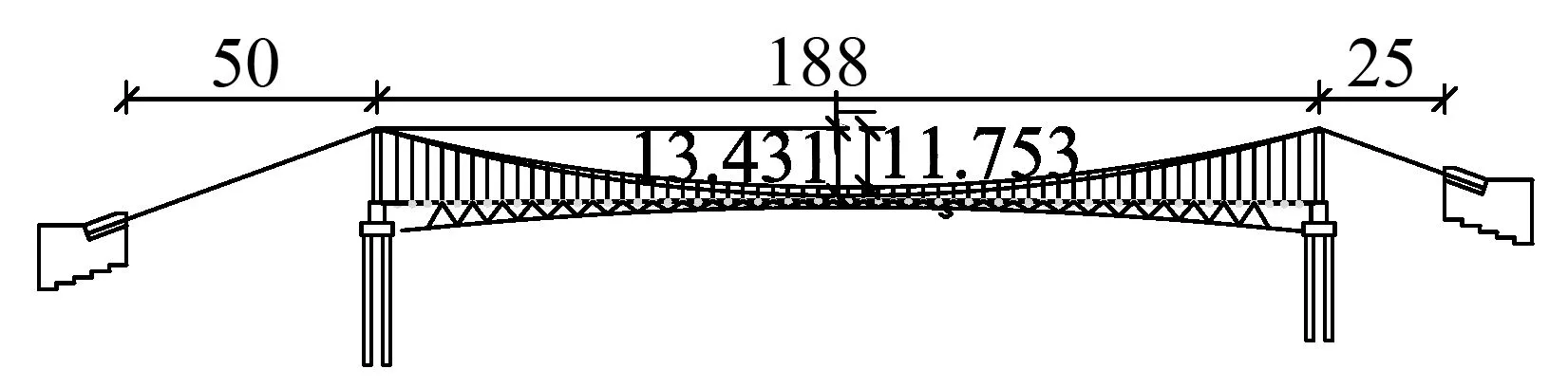
(b) 双缆悬索桥 单位:m
图1 不同结构体系立面布置
2 有限元模型
采用有限元软件Midas/Civil建立整体空间模型,根据模型的基本参数进行网格划分,将单缆悬索桥模型划分为595个节点,840个单元,其中主缆和吊杆共250个单元。双缆悬索桥模型共划分720个节点,1 084个单元,其中主缆和吊杆单元数493个。两种体系采用相同的边界条件,主塔顶横梁和主缆之间采用刚性连接,塔底及主缆锚固处采用固结[6-7]。表1为悬索桥各主要构件材料参数。模型示意见图2。

表1 悬索桥主要构件参数

图2 模型示意
3 结果分析
3.1 成桥状态
主缆是悬索桥的主要承重部位,恒载通过吊杆向主缆传递,然后传递给锚碇和基础[8-10]。根据建立的有限元模型,成桥状态下不同体系的主缆内力见表2。

表2 不同体系下的主缆内力 kN
由表2可知,单缆和双缆体系下的左边跨塔顶主缆张力分别为1 151.9 kN和1 245.1 kN。采用双缆体系对矢高的要求更高,桥塔高度的增加能加大主缆与水平线的夹角。在成桥阶段,双缆体系下主跨主缆的张力为1 195.8 kN,单缆体系下主缆张力为1 107.3 kN,差距8%,较为接近。
3.2 人群荷载作用分析
本桥人群荷载按3.5 kN/m2计,利用Midas/Civil将人群荷载均匀加载到桥面板[11-12],获得主缆内力的分配情况如表3所示。

表3 人群荷载下的主缆内力 kN
由表3可知,单缆体系下主跨塔顶主缆张力为1 218.7 kN,双缆体系下主跨塔顶顶缆最大张力为550.8 kN,底缆最大张力为708.0 kN。单缆体系下主跨跨中主缆张力为1 175.2 kN,双缆体系下主跨跨中顶缆最大张力为535.1 kN,底缆最大张力为681.6 kN。这表明在人群荷载作用下,底缆分担的荷载更多,约为顶缆的1.3倍。
单独选出主梁单元,获得人群荷载作用下的主梁弯矩包络图如图3所示。从图3可以看出,两种体系下主梁的弯矩变化趋势近似,除桥塔及梁端外,其余截面弯矩变化幅度不大。相对于单缆体系,双缆体系下主梁的弯矩变化更趋于稳定,且除跨中正弯矩有一定提高外,其余截面弯矩均出现不同程度的下降。

(a)单缆体系

(b)双缆体系
人群荷载作用下主梁竖向挠度如图4所示。从图4中可以得出,两种体系下主梁的竖向挠度变化情况近似,挠度曲线呈W形,在1/4L和3/4L处取得最值。双缆体系下最大下挠为319.5 mm,单缆体系下最大下挠为367.8 mm,减小约15%。

(a)单缆体系

(b)双缆体系
3.3 风荷载作用分析
本桥风速根据规范P=1/100取值,风速为26.0 m/s,风压为0.423 kN/m2,计算得到横向风荷载值[13-14],获得风荷载作用下的梁端位移和塔底弯矩见表4。从表4可以得出,单缆体系下梁端位移106.597 mm,双缆体系下梁端位移75.305 mm,减少了29.4%。单缆体系塔底弯矩为221.1 kN·m,双缆体系的塔底弯矩为157.2 kN·m,减少了28.9%。

表4 风荷载下的梁端位移和塔底弯矩
横风荷载作用下,不同体系的主梁弯矩如图5所示,挠度见图6。从图中可以得出,两种结构体系下主梁弯矩和挠度的变化趋势比较相似。双缆体系下最大正弯矩为3.28 kN·m,跨中挠度为311.2 mm。单缆体系下最大正弯矩为4.54 kN·m,跨中挠度为357.3 mm。弯矩减小了27.8%,挠度减小了12.9%。

(a)单缆体系

(b)双缆体系

(a)单缆体系

(b)双缆体系
3.4 自振特性
对悬索桥来说,自振特性对结构体系安全性至关重要。利用有限元软件Midas/Civil构建两种不同结构体系下的整体空间模型,提取前十阶频率进行对比分析[15-16],如表5所示。

表5 前十阶自振特性 Hz
由表5可知,单缆体系的1阶对称侧弯频率为0.173 5 Hz,双缆体系的1阶对称侧弯频率为0.185 Hz,增加了6.6%。此外,双缆体系的竖弯频率、竖振频率以及侧振频率均有所提高,安全性能得到加强。
4 结论
双缆悬索体系与传统单缆悬索体系存在较大差异。依托某大跨度钢结构人行悬索桥实际工程,利用有限元分析软件对结构进行整体建模,对不同结构体系进行性能分析,主要结论如下:
(1)人群荷载作用下,双缆体系中底缆承担更多荷载,主梁弯矩变化稳定,挠度相比单缆体系减小15%。
(2)横风荷载作用下,两种结构体系下主梁弯矩和挠度的变化趋势比较相似,双缆体系的弯矩和挠度均小于单缆体系。
(3)双缆体系的侧弯频率、竖弯频率、竖振频率和侧振频率相比单缆体系均有所提高。双缆体系具有更优的力学性能,安全性更高。

