双行星排行星齿轮偏转力分析及其应用

包寿红， 张彤， 王晨， 余才光， 陶伟， 刘一

（科力远混合动力技术有限公司 上海分公司，上海201501）

0 引 言

汽车节能减排是当今汽车技术重要研究方向之一，尤其是节能技术。为了提升传统能源汽车节能水平，促使新能源汽车产业发展，有效缓解能源和环境压力，国家为此出台了汽车双积分政策；《中国制造2025》也提出2020年每百公里5 L油耗的标准，在2025年达到每百公里4 L的标准。在此背景下，新能源汽车已成为国内各主机厂的重点研发工作。

新能源汽车的关键核心是动力耦合系统。目前国内各主机厂比较广泛使用的是串并联混合动力方案，但串并联方案的混合动力系统有其优点也有缺点，节能效果有一定的局限性。丰田的THS主要采用了行星排复合分流的混合动力系统，其主要优点是发动机与车速解耦，通过电动机全程对发动机工作点进行优化，确保发动机始终可以工作在最佳工作点上，达到最佳节油效果。

以行星排为动力的耦合装置，比较常见有单行星排结构、拉维纳双行星排结构等。不论哪种结构，均由太阳轮、行星轮及齿圈三部分构成。太阳轮、行星轮一般采用斜齿圆柱齿轮，由于斜齿齿轮在传动过程中会产生轴向和径向分力，这两种分力会产生一个与行星轮轴线呈一定偏转角度的合力，容易使齿轮传递过程中出现倾斜，造成齿轮啮合度变差，出现止推垫片、销轴和齿轮等磨损，带来行星排传动效率下降、传动异响甚至失效等问题。

1 行星齿轮受力分析

1.1 斜齿圆柱齿轮受力特点

如图1所示[1]，作用在齿面上的法向力Fn可分为3个互相垂直的分力,即圆周力Ft、轴向力Fa和径向力Fr。Fn作用在齿廓的法面内，法面与端面的夹角为β，法面压力角为αn。其中Fr′为轴向力Fa和径向力Fr的合力，与行星轮端面成θ角。

图1 斜齿圆柱齿轮受力情况

由图1中的关系可得：

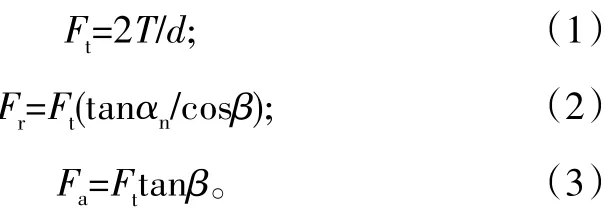
轴向力Fa和径向力Fr的合力为Fr′,力的大小和该力与齿轮端面的夹角θ为:

为便于描述，合力Fr′称为斜齿圆柱齿轮的偏转力, 该力与齿轮轴线的夹角θ称为齿轮的偏转角，偏转力的方向取决于齿轮螺旋线方向和齿轮的转动方向。

1.2 行星齿轮偏转力分析

由于行星齿轮存在偏转角为θ的偏转力Fr′，如果销轴与行星轮内圆配合上有一定的径向间隙，间隙大小为d1,行星轮运转过程中就会以销轴和滚针轴承接触的一端为支点O发生偏转，如图2所示[2]。

图2 行星齿轮受力情况

在图2中，行星轮长度为L，行星轮内圆与销轴的配合间隙（径向间隙）为d1，行星轮端面与止推垫片的轴向配合间隙为d2，销轴外径为d3，当行星轮偏转时，如行星轮轴向尺寸变化的大小在轴向间隙d2的范围之内，则行星轮所能偏转的角度φ主 要 取 决于径向间隙d1。为了能求出行星轮偏转时对止推垫片的轴向压力N1及以销轴和滚针轴承接触的一端为支点处的压力N2，需对图2进行简化,如图3所示，其中：R为行星轮半径；r为止推垫片的半径；纵轴y为销轴过支点O的轴线；γ角为压力N2与x轴向夹角，依据有关三角关系，可计算出γ。

式中：L1=r-d3/2;L2=R+d3/2。

在行星轮偏转时，偏转的角度φ可通过式（7）进行计算：

由图3行星齿轮偏转角φ≠0的受力情况，根据力矩关系可得N1的值为

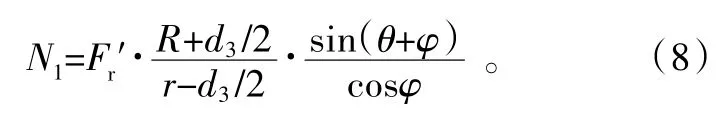
为求出对销轴的压力N2值，可将N1与Fr′平移到支点O上，如图4所示[3]，通过正交分解，可求得

图3 行星齿轮偏转时受力情况

图4 行星齿轮偏转时受力情况

2 行星齿轮问题

图5所示为某行星排耦合装置在台架耐久试验中出现异响问题后的拆解情况，滚针轴承、行星轮止推垫片及销轴等出现不同损坏。

图5 行星齿轮拆解图示

根据上述斜齿圆柱齿轮存在偏转力的特点，当滚针轴承与销轴间存在一定间隙时，齿轮将发生偏转，如图6所示。左偏转时，齿轮与止推垫片形成点接触，止推垫片应力增大出现磨损；同时滚针轴承偏转，上部分（箭头所示）与销轴点接触，应力也同时增大，造成销轴磨损，滚针轴承损坏。同理，行星轮右偏转时，齿轮与止推垫片形成点接触，滚针轴承与销轴下部点接触，应力增大出现磨损。

由于齿轮偏转，齿轮之间啮合力变差，加之滚针轴承损坏等原因，造成齿轮磨损。

3 行星齿轮问题分析与验证

3.1 双行星排功率分流装置

图6 行星齿轮偏转应力图示

图7 为某混合动力系统双行星排功率分流装置，采用变形的拉维纳式行星排结构，具有齿轮数量较少且结构紧凑。该结构可以分解为共用行星架C和齿圈R的一个前行星排和一个后行星排，且前行星排的行星轮和后行星排的行星轮相啮合。

图7 双行星排功率分流装置

图7中，小太阳轮S1、短行星轮P1以及外齿圈R构成齿轮机构的前行星排，大太阳轮S2、长行星轮P2、短行星轮P1和外齿圈R构成齿轮机构的后行星排。行星架C与发动机连接，小太阳轮S1与小电动机EM1相连，大太阳轮S2与大电动机EM2相连。根据行星齿轮有关运动学和动力学关系，可得行星排的转速和转矩特性方程如下：

式中：ωs1、ωs2、ωR、ωC分别为小太阳轮、大太阳轮、外齿圈R和行星架C的角速度；i01为前排行星轮速比，i01=-ZR/ZS1；i02为后排行星轮速比，i02=ZR/ZS2，ZR、ZS1、ZS2分别为齿圈与大小太阳轮齿数；Ts1、Ts2、TC和TR分别是作用在大小太阳轮、行星架和齿圈上的转矩。

以上相关参数可以在图8的等效杠杆图表示。

3.2 车辆行驶过程中行星齿轮受力分析

汽车耐久性试验是为了考核整车、系统、子系统和零部件可靠性的一组试验，是整车设计开发过程中不可缺少的重要环节。耐久性试验一般主要包括高环路段、坡道路段、强化坏路和综合路段等，其中的组合路段、坡道和综合道路这两个工况属于比较恶劣的工况。图9所示为某车型综合工况下齿圈输出转矩波形图，转矩幅值变化大，对行星排要求很高。

图8 双行星排等效杆杠

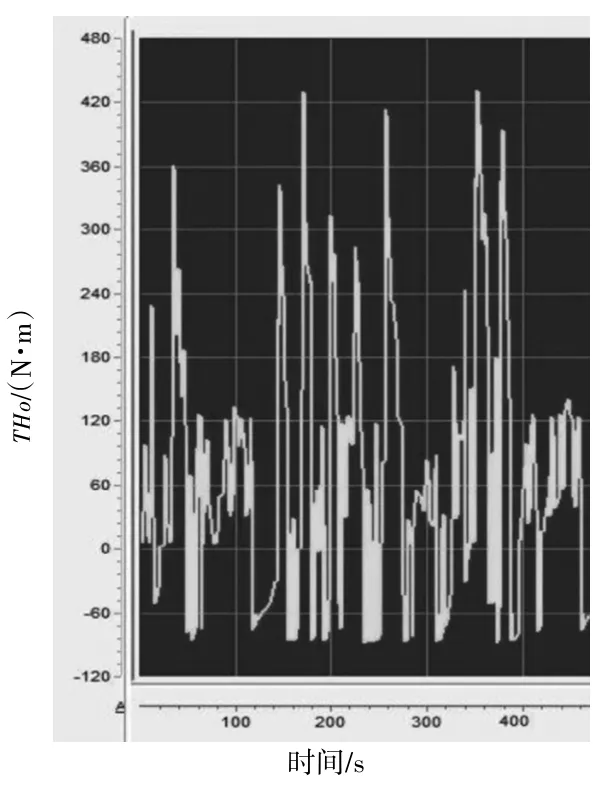
图9 综合工况下齿圈输出波形

混合动力处于中高速运行模式时，此模式下B2锁止，杠杆平衡转矩由B2制动器提供，小电动机不工作，大电动机提供驱动或制动转矩，发动机提供驱动转矩，等效杠杆图参考图8。混合动力模式的数学模型[4]为

TMG1、TMG2分别为小电动机和大电动机输出转矩，TENG为发动机驱动或阻力转矩；Tf为整车阻力矩；rS1、rS2、rR分别为小太阳轮、大太阳轮和齿圈半径；IS1、IS2、IMG1、IMG2、IR分别为小太阳轮、大太阳轮、小电动机和大电动机以及齿圈的转动惯量；Ft1，Ft2分别为前、后排轮系齿轮啮合力；m为整车质量；R为轮胎半径；K为主减速器传动比。

根据图9轮边转矩波形，THo依次取0 N·m、60 N·m、120 N·m、180 N·m、240 N·m、300 N·m负载。为便于简化分析，设定控制系统以图8等效杠杆图的模式实现0～60 km/h加速，则根据式（13）数学模型可求出对应的后排轮系齿轮啮合力Ft2的值，根据式（8）和式（9），可求出在图9的综合工况下，行星轮偏转时对止推垫片的轴向压力N1，以及与滚针轴承接触一端销轴的压力N2，如图10所示，以此确定滚针轴承与止推垫片的应力特点。

图10中，THo载荷在60 N·m时，发动机未介入工作，系统处于纯电模式，120 N·m后发动机工作进入混合动力模式；随着THo载荷的增大，行星齿轮圆周力Ft2、行星轮偏转时对止推垫片的轴向压力N1，以及与滚针轴承接触一端销轴的压力N2也成正比增加。

正常情况下，行星齿轮不会产生偏转，滚针轴承所受的应力为

式中：Fr为作用在轴承上的径向载荷；S为轴承承载的面积。

由于滚针轴承与销轴间存在一定间隙，行星齿轮发生偏转，滚针轴承承受的载荷将变为N2（大于Fr），滚针轴承与销轴也变为点接触，承载面积S大幅减小至一点。由于轴承承载面积越小，表面应力越高，轴承寿命越低，这种特殊情况下，滚针轴承所受的应力将远远超出设计时滚针轴承的许用应力，造成销轴磨损，滚针轴承损坏。

行星齿轮偏转的同时，行星齿轮端面与止推垫片的接触面积也减小，在轴向压力N1的作用下，止推垫片也出现磨损发热，润滑变差，最终出现止推垫片烧蚀现象,影响齿轮传动。

图10 0～60 km/h加速过程行星齿轮受力特点

3.3 验 证

通过以上原因分析，要避免出现滚针轴承和垫片磨损，主要是要减小滚针轴承与销轴的间隙，避免出现齿轮倾斜，同时调整齿轮的压力角、螺旋角等，减小齿轮的偏转角度和轴向力，并根据实际情况改善滚针轴承的润滑、调整齿轮径向间隙等，图11是改进后通过耐久试验后拆解的销轴与垫片，没有再出现如图5所示销轴磨损和垫片烧蚀的现象，说明主要通过调整滚针轴承与销轴间隙等措施，可以较好地避免出现以上问题。

图11 改进并通过耐久试验的拆解图片

4 结 论

综上所述，由于斜齿圆柱齿轮传动过程中，存在偏转力矩，如果销轴与滚针轴承的径向间隙过大，将促使齿轮发生偏转，造成齿轮端面与垫片间以及滚针轴承与销轴间接触面变小，在大载荷恶劣工况下，齿轮端面对垫片的压力和摩擦力剧增，发热严重，最终出现垫片烧蚀及销轴磨损的问题。

为避免出现以上问题，根据上述原因分析，可以考虑从以下几个方面进行改进：

1）斜齿圆柱齿轮传动过程中，始终存在偏转力现象，根据式（7），为了避免齿轮倾斜，要严格控制齿轮内圆与销轴间的径向间隙d1以及轴向间隙；

2）根据式（2）、式（4）、式（5），可以适当调整齿轮的压力角an与螺旋角β，减小齿轮的偏转角和偏转力及对垫片产生的压力；

3）根据式（8），需要严格控制齿轮端面和垫片表面的粗糙度，选用合适的材料，减小齿轮端面和垫片之间的摩擦因数；改进齿轮端面与垫片间的润滑和散热条件，避免垫片出现过热烧蚀；

4）根据式（14），可适当增加滚针轴承的承载面积，减小应力，同时改善滚针轴承的润滑条件，避免出现磨损。