馈能悬架并联机构静力学分析

付延轩, 李鑫军, 刘之涵

（青岛理工大学, 山东 青岛266520）

0 引 言

馈能悬架是一种新型主动悬架系统，是指利用馈能装置（目前主要分为电磁式、油气式和机械式馈能三种）替代传统的悬架减震器，将车辆车身因为路面不平度产生的震动能量回收并加以利用。自20世纪90年代，国内外专家学者纷纷加入馈能悬架能量回收研究的行列，从馈能机理、系统结构和控制算法上不断进行改善，但并未取得满意的效果[1-3]。

2012年伊朗学者Reza Sabzehgar等[4]第一次在汽车馈能悬架系统中引入少自由度并联机构。少自由度并联机构是一种新型并联机构，其自由度在2～5之间，具有传统的串联机构所无法比拟的优点，是串联机构的补充和扩展，其具有轻便灵活、结构简单、制造成本低廉、容易操控等优点[5]。但是，少自由度并联机构也会因其自由度的减少而造成机构的耦合运动，运动学和动力学分析变得十分困难。2013年黄真等[6]建立了少自由度运动学模型，模型的建立利用了虚设机构法，并且首次将影响系数法运用到分析并联机构运动学当中。2017年柳江等[7]以少自由度并联机构为研究对象，建立了馈能悬架的动力学模型，验证了所建模型的正确性，但没有进一步分析其静力学特性。

文中研究的是一种少自由度并联机构的静力学分析，该机构是末端执行平台（以下简称执行平台）沿z轴上下移动，旋转动基座（以下简称动基座）绕z轴来回转动的模型，利用坐标转换法得到位置逆解，然后利用拆杆法进行静力学分析[8-10]，得出该机构的静力学平衡方程，通过求解该方程，得出了该机构每个杆件的全部约束力与力矩。通过SolidWorks软件进行建模，导入ANSYS平台中对并联机构进行结构静力学仿真分析。

1 少自由度并联机构机构分析

1.1 少自由度并联机构描述

馈能悬架系统的基本工作原理是将由于路面不平度所造成的车身垂向运动而产生的能量，通过并联机构转化为可以带动馈能电动机工作的旋转运动，从而使振动能量转化为电能储存在蓄能元件中，其优点是提高了回收能量效率，能够及时补充车辆电子设备和悬架主动控制所消耗的电能[11]。如图1所示，建立2自由度1/4汽车馈能悬架模型。

图2为少自由度并联机构示意图，其由执行平台A，动基座B，3条分支支链li（i=1，2，3）和一条中间约束支链l4组成。执行平台和动基座上的球铰副A1A2A3，B1B2B3相对于两平台的中心点均匀分布。执行平台A上的球铰副Ai与动基座B上的球铰副Bi的连接都是由A1B1，A2B2和A3B3等3条支链通过连杆完成的，中间约束支链l4上端与执行平台的连接处通过移动副与车辆车身链接，另一端与动基座的连接处则通过旋转副与馈能电动机链接。

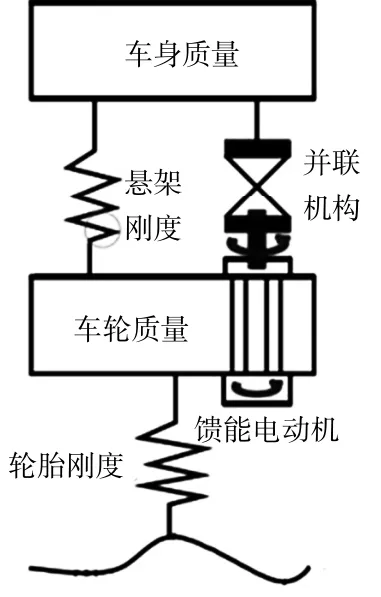
图1 二自由度1/4汽车馈能悬架模型

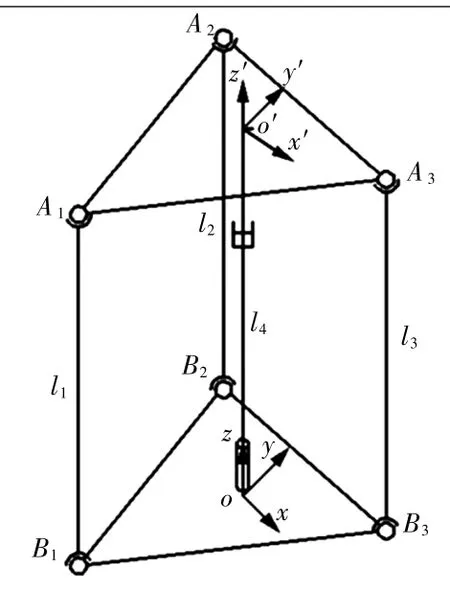
图2 少自由度并联机构示意图

1.2 位置分析

目前大多数并联机构采用上平台运动下平台静止的机构，此机构与大多数并联机构不同，其包含上下两个动平台，为了实现与之相似的结构，利用坐标变换法将参考坐标系固连在动基座上。如图2所示，分别以动基座和末端执行平台的几何中心为原点，建立参考坐标系系o（x,y,z）和动坐标系o′（x′,y′,z′）。O点位于B1、B2、B3组成的正三角形的中心，x轴与z轴分别平行于B1B2与中心轴线，y轴方向按右手定则确定。执行平台建立的坐标系中：x′轴//x轴，y轴′//y轴，z′轴//z轴。

利用坐标变换法，末端执行平台坐标系o′（x′,y′,z′）的坐标可以转化为动基座坐标系o（x,y,z）的坐标，表达式为

动坐标系中，Ai(1,2,3)的坐标表达式为：

参考坐标系中，Bi(1,2,3) 的坐标表达式为：

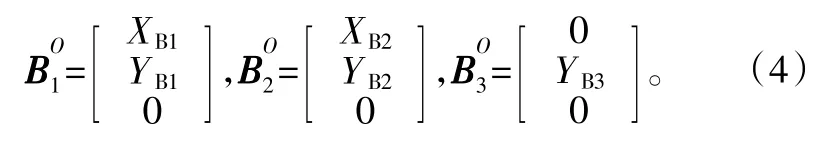
由几何关系可得少自由度并联机构的位置逆解方程为：

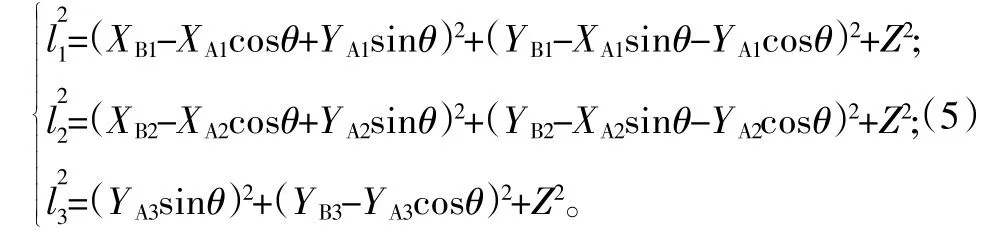
方程组（5）中，l1，l2，l3，θ，z是关于位置逆解方程的几个重要因素，并且该机构的初始位置取决于参数θ、z。

2 并联机构静力学分析

利用传统拆杆法对并联机构进行静力学分析，在分析之前，先对其进行几点假设：假设各铰接处的变形和摩擦力忽略不计；假设各杆件受力引起的变形忽略不计；假设上下平台的刚度非常大。将并联机构分为分支支链l1、l2、l3，中间约束支链l4，以及末端执行平台，下面分别对其进行具体分析。

2.1 分支支链的受力分析

分支支链向量i（i=1,2,3）在参考坐标系o（x,y,z）中的位置关系如图3所示。

如图4所示，设整个驱动分支支链li的质量为m，先将其作为整体进行分析，然后求固定铰接点Bi的质量矩，最后可以求出驱动分支支链的质心lci位于连杆li的1/2处。分支支链在参考坐标系o（x,y,z）的受力分为，Fg=mg为分支支链自身的重力，Fi=(Fxi Fyi Fzi)T(i=1,2,3)为动基座对其连接的球铰副的约束反力，Fj=(Fxj Fyj Fzj)T(j=4,5,6)为末端执行平台对其连接的球铰副的约束反力。

图3 少自由度并联机构驱动分支支链向量方位图

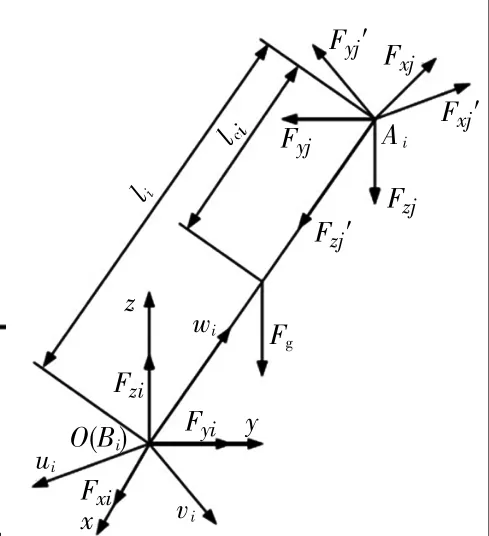
图4 分支支链受力图

分支支链li的静力平衡方程表示为：

在局部坐标系Bi（ui,vi,wi）下，且=R·j，对分支支链li的固定铰接点Bi取矩，力矩的平衡方程表达式为

在局部坐标系下，标量表达式为：

结合式（7）、式（8），在参考坐标系o（x,y,z）下的力矩平衡方程可以整理为：

2.2 中间约束支链的受力分析

如图5所示，中间约束支链在参考坐标系o（x,y,z）的受力为：中间约束支链的重力为Fg=mg，中间约束支链的长度为l7；中间约束支链与末端执行平台连接的移动副受到其约束反力Nj′=(Nx7′Ny7′ 0)T与 约 束 力 矩Mj′=(Mx7′My7′Mz7′)T，中间约束支链与动基座连接的旋转副受到其约束反力Nj=(Nx7Ny70)T与约束力矩Mj=(Mx7My70)T。

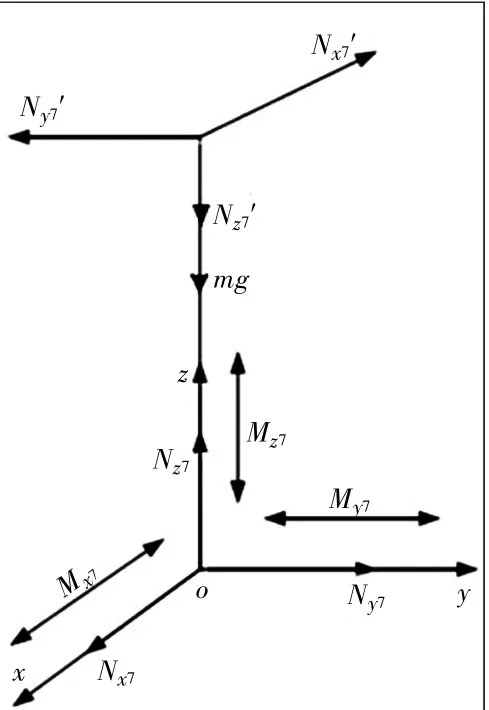
图5 约束支链受力图

当中间约束支链处于静力平衡状态时，力平衡方程可以表示为

对动基座质心O取矩，力矩平衡方程可以表示为

结合式（10）、式（11），在参考坐标系o（x,y,z）下的力矩平衡方程可以整理为：

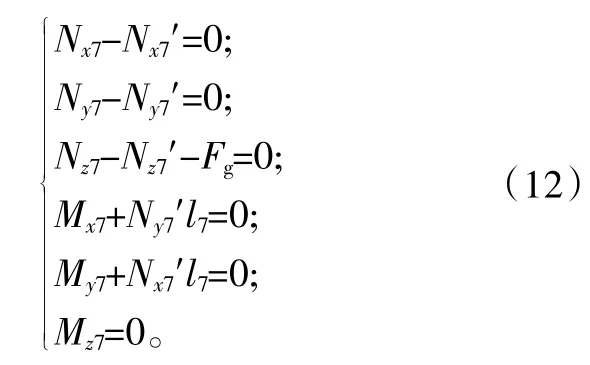
2.3 执行平台的受力分析

如图6所示，末端执行平台在参考坐标系o（x,y,z）的受力为：末端执行平台的重力为Fg′=mg，末端执行平台的长度为l7；末端执行平台与末端执行平台连接的移动副受到其 约 束 反 力Nj′=(Nx7′Ny7′ 0)T与 约 束 力 矩Mj′=(Mx7′My7′Mz7′)T，末端执行平台与动基座连接的旋转副受到其约束反力Nj=(Nx7Ny7Nz7)T与约束力矩Mj=(Mx7My70)T。

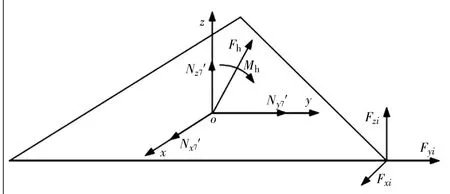
图6 执行平台受力图

当末端执行平台处于静力平衡状态时，力平衡方程可以表示为

对末端执行平台的质心O，力矩平衡方程可以表示为

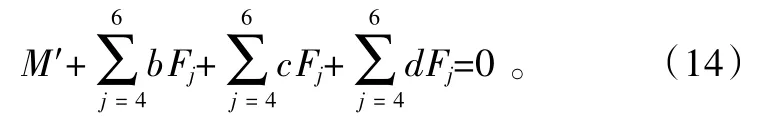
结合式（13）、式（14），在参考坐标系o（x,y,z）下的力矩平衡方程可以整理为：

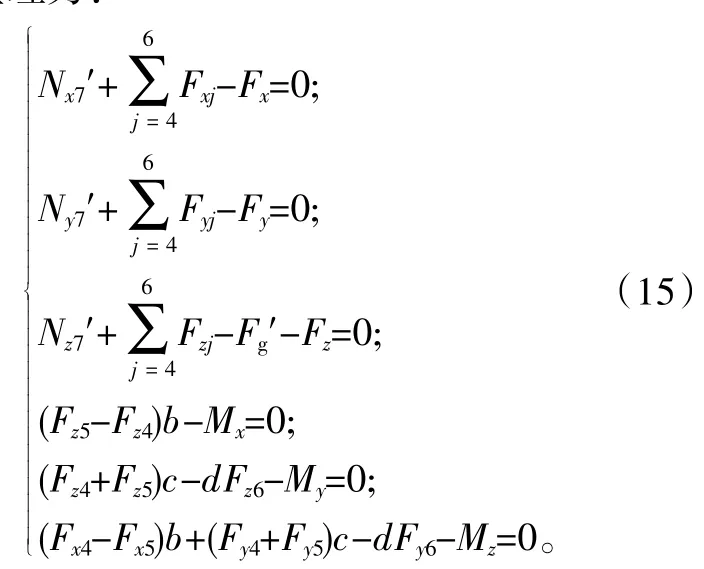
联立静力平衡方程（6）、（9）、（12）、（15），可以组成一个（6×5-3）维方程组，该方程组中包括27个未知力和力矩（3条分支支链分别有6个未知力，中间约束支链有9个未知力和力矩），可见，方程的个数和未知力、力矩的个数相等，所以少自由度并联机构的静力学平衡方程为静定方程，通过方程组即可求出少自由度并联机构中的所有力和力矩。

3 静力学仿真分析

本文选用SolidWorks软件对并联机构进行实体建模，结构参数如表1所示。

将在SolidWorks 软件中建立好的少自由度并联机构的实体模型，进行模型简化，然后导入到有限元软件平台中，为了得到结构静力学分析的结构，首先要设置以下参数：1）定义材料参数和单元属性。该并联机构的材料选择为结构钢，密度为7.9×103 kg/m3，弹性模量为211 GPa，泊松比为0.3，实体单元定义为Solid187。2）进行网格划分。设置网格尺寸为3 mm。3）加载约束条件。将动基座与地面固连，在分支支链的各个球铰处加载球副连接，在中间约束支链与执行平台间加载移动副约束，与动基座间加载旋转副约束。4）加载载荷。在末端执行平台上施加沿Z轴竖直向下1000 N的力。

经过有限元软件平台的仿真计算，得到少自由度并联机构的应力和变形云图，如图7～图8所示。通过图7分析总体和各部件应力云图可知，机构的等效应力最大值为34.42 MPa，发生在连杆与末端执行平台的连接处。已知该机构材料的屈服强度极限为235 MPa，该应力远远小于其屈服极限，属于弹性变形，所以此机构完全满足使用的需求。通过图8分析机构的总体和各部件变形可知，变形最大的位置发生在末端执行平台的尖端，最大变形量为0.13 mm，其次为连杆与球铰连接处，变形量为0.12 mm，其它位置变形量都比较小，以上数据可以为馈能悬架并联机构的进一步优化设计提供一定的理论依据。

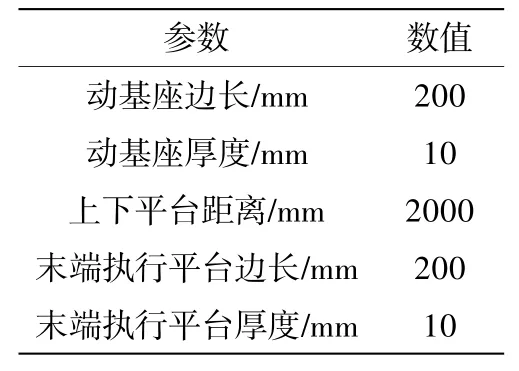
表1 结构参数

图8 少自由度并联机构变形云图

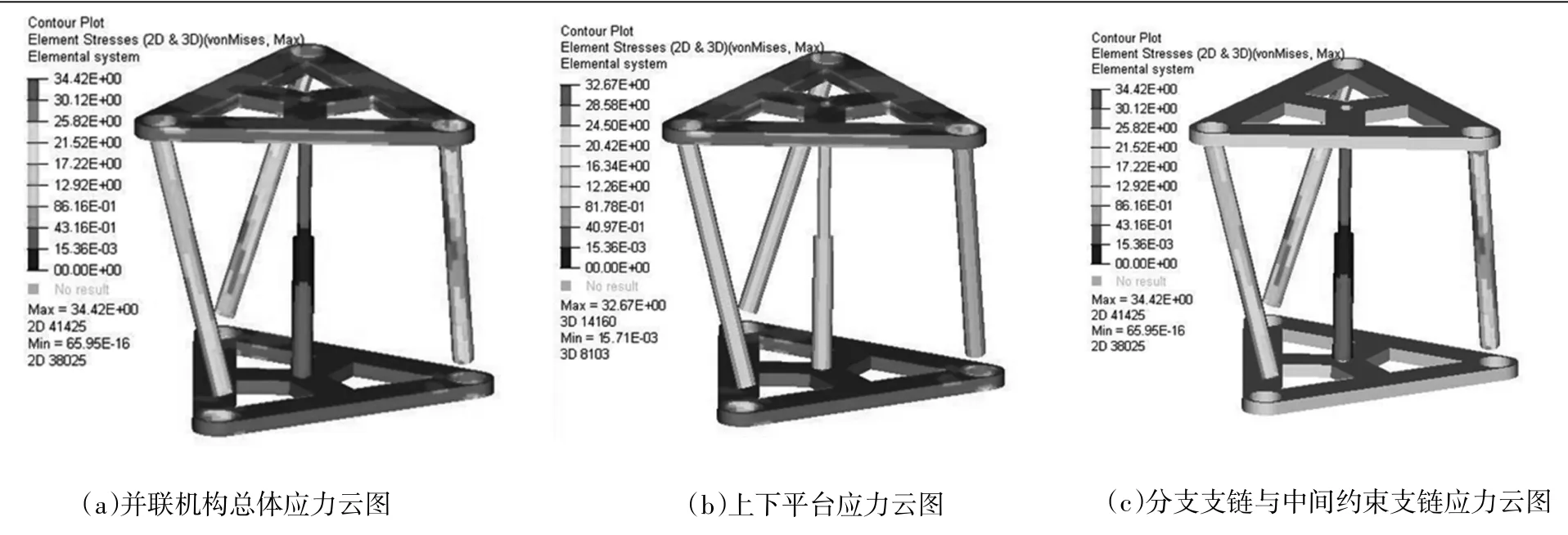
图7 少自由度并联机构应力云图

4 结 论

1）提出一种简单的二自由度并联机构，利用坐标变换法建立位置逆解方程，通过拆杆法，得到了少自由度并联机构的静力学平衡方程，得到其静力学数学模型，求解得出该机构的所有力和力矩。

2）通过SolidWorks建模和有限元软件的静力学仿真分析，结果表明，少自由度并联机构的最大应力值和最大变形值均远小于机构材料的屈服强度极限和变形极限，为并联机构的优化设计提供了一定的理论依据。