基于EMD-ICA的风电机组信号盲分离研究

陈长征， 白旷甲

（沈阳工业大学机械工程学院，沈阳110870）

0 引 言

传统的噪声识别方法已经不能满足现代实际工程中遇到的噪声难题，而近年来现代数字信号处理方法多被采用在实际工程中并取得了满意的效果与精度。

根据风力发电机组的工作环境特点，采集到的振动噪声信号往往都伴随着各种冲击等瞬态变化，传统方法中的频谱分析不适用来针对一些非稳态信号，不能满足噪声源识别的要求。以常用的两种时频分析方法为例，小波变换和短时傅里叶变换由于Heisenberg测不准，只能获得部分频段的时频，在全频段上存在分辨率不足的缺点。对于非线性非稳态信号的处理，最早由美籍华人N.E.Huang[1]于1998年提出了经验模态分解方法。风力机的噪声源来源广泛，由于整个机组的机械部件非常多，且采集信号的实验条件有所限制，往往测得的混合信号在复杂的运行状态中存在某些噪声源的频谱相互重叠的情况，小波变换、EMD等方法难以将重叠的特征频率分离开来，从而导致识别失败。该方法的原理即可以把原始混合信号通过循环筛选后分解为一组固有模态分量[2]。根据风力机振动信号的复杂特点，宜采用盲源分离手段来处理。独立分量分析算法是其中应用最广泛的方法[3]，最早是为了解决“鸡尾酒会”问题[4]而提出的。本文就采用EMD与ICA相结合的手段来对复杂的风力机信号进行盲分离。

1 盲分离简介

1.1 盲分离原理

盲信号处理一般是指在信号源特性与其传递过程都未知的条件下，对采集到的混合信号进行处理得到其中源信号的方法。由于传递过程未知，所以它只能根据观测信号来进行一些变换来提取源信号[5]。简单表示盲信号的处理过程如图1所示，通过系统的输出 来估计传递函数和输入 。其中传递函数 与 未知，表明要提取的源信号的特性参数可以不必知道，各个源信号的输入混合方式及其传递过程也不必已知。

1.2 盲分离数学模型

根据上面提到的风力机组的实际工作环境与工况以及测量条件，对风力机组的噪声源识别问题属于欠定盲源分离问题，所以选择采用线性瞬时混合模型来进行盲分离处理。线形瞬时混合盲源分离模型如图2 所示。

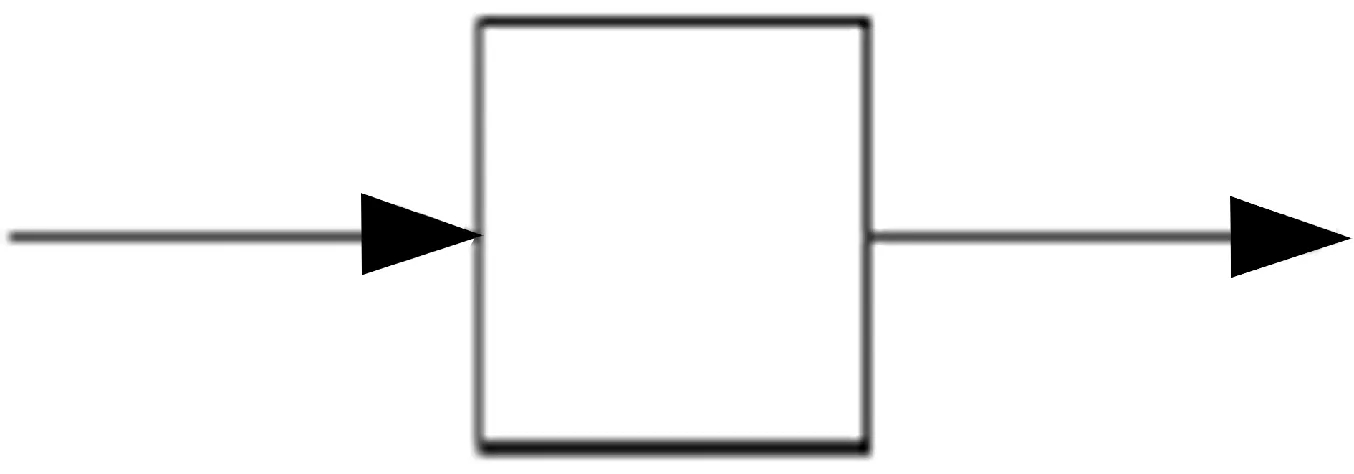
图1 盲分离的简单原理框图

图2 线性瞬时混合盲分离模型

其中，（t）是m维向量组成的信号源组，通过混叠系统 计算得到m维向量（t），设（t）是m维的附加噪声，忽略延迟，得到观测信号，用下式表达：

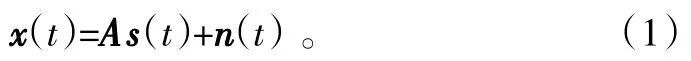
通过分离系统 分离出估计源信号（t）=（t），这也是盲源信号分离的最终目标，而实际上能够求解和准确确定分离矩阵 是盲分离算法的主要研究方向。若将噪声信号看成一个普通的源信号混合其中，将噪声分离出来也可看做此一种有效的降噪。

2 独立分量分析及Fast Ica 算法

1997 年芬兰著名学者经过不懈地研究与实验，创造性地提出了基于负熵的独立分量分析的固定点算法[6]。此方法具有显著的收敛速度较快、收敛性好的优点，后来此法被广泛称为快速独立分量分析算法[7-8]。为了求解混合系统的分离矩阵，ICA优化算法主要包含三个主要步骤：混合原始信号的预处理；确立优化判据；最后根据优化判据建立算法。预处理通常分为中心化处理与白化过程。要使白化处理后的信号各个分量i之间相互独立，其主要变换如下：

根据上面描述可知分量 具有单位方差，计算方差如下：

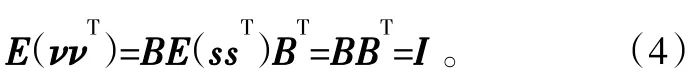
有上面表达式可知 为正交矩阵，于是问题就从求解矩阵变成了求解正交矩阵 ，然后就可以估计源信号向量：

3 风电机组混合信号的经验模态分解

传统时频分析方法难以处理风电机组这样具有重叠噪声频率的混合非稳态信号，在20世纪90年代末Nordon E.Huang等学者提出了经验模态分解法，可以将混合信号进行分解，得到一组具有物理意义的固有模态分量[9]。此方法可以有效地处理和分析非稳态信号。由于此对非线性非稳态信号处理上的优点，EMD符合用来处理大型风力机组的复杂噪声。

经验模态分解算法主要包括以下几个步骤：

1）计算信号数据序列内的所有极值点。

2）通过插值拟合极大值点后得到上包络线u（t），同样地通过插值拟合极小值点后得到下包络线l（t）；

3）求得上包络线与下包络线平均值m1（t）：

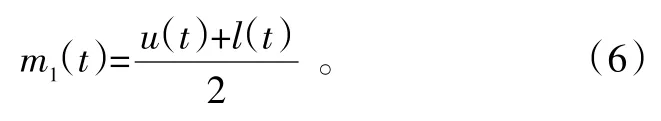
4）将要分析的源信号x（t）与m1（t）作差得到：

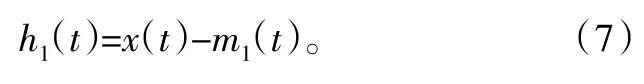
若h1（t）是固有模态分量，那么它应包含本征模函数所具有的物理意义，否则就是无意义的一个分量。为保证分解后的波形有较好的对称性，往往需要进行重复筛选，当残余信号中不再能够提取出本征模函数或残余信号称为一单调趋势量时，停止筛选过程。

5）将上一步得到的h1（t）重新被当做信号进行筛选：

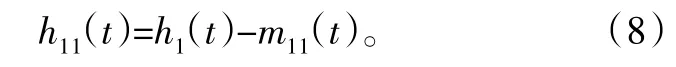
经过k次筛选，h1k（t）就是一个固有模态分量：

其中c1（t）包含被分析信号的最短周期分量，它实际上是源信号x（t）中最高频部分。将c1（t）从x（t）中分离出来，剩余信号记为r1（t）：

重复上述计算过程进行筛选：

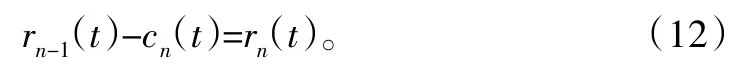
直到满足设定的分离标准停止筛选，最终信号：

这样原始的信号x（t）被分解为n个固有模态分量和一个余项分量。整个过程的流程如图3所示。

4 风电机组信号预处理的仿真实验分析

为验证此算法的效果，对上面提出的去干扰算法进行仿真验证。要将弱信号含有干扰信号的混合信号中分离出来，给定干扰信号的频率为25 Hz、100 Hz、50 Hz，要识别的弱信号频率为75 Hz，并附加白噪声40 dB，它们的混合过程如下式：

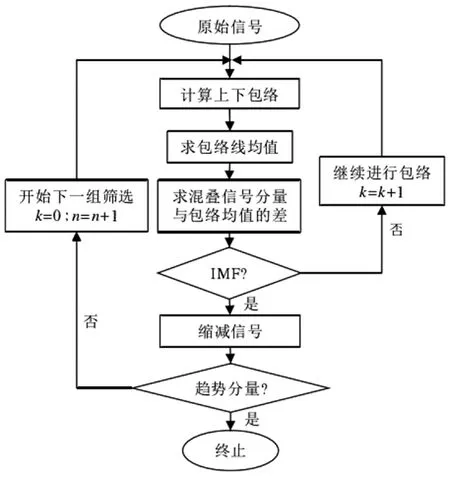
图3 经验模态算法（EMD）流程图

其中采样频率为1000 Hz，采样点数为1024。图4为源信号的波形和频谱图。用软件得到此混合信号的频谱图与波形图。如图4所示，可以明显看出三个强信号的频率，但是弱信号埋没其中无法预知。

图4 混有强信号的原始信号波形图和频谱图

从图4 频域图可以清晰地识别三个干扰信号，然后将它们与x（t）通过随机混合矩阵 组成新的混合信号然后采用Fast Ica 算法将混合信号进行分离得到图5。图5（a）、图5（c）、图5（e）为强干扰信号的波形图，图5（b）、图5（d）、图5（f）为干扰信号（频率为100 Hz、50 Hz、25 Hz）频谱图，图5（g）是我们想得到的弱信号的波形图，图5（h）为其对应的频谱图（频率为75 Hz）。

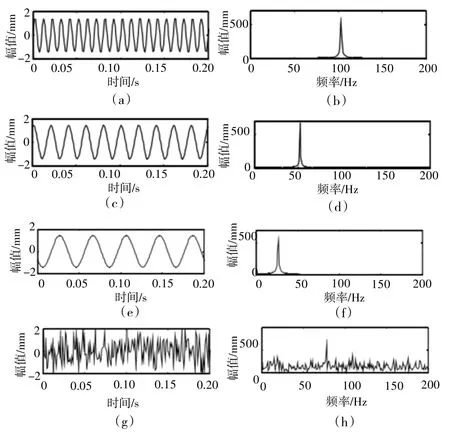
图5 FastIca分离之后信号的波形图与频谱图

从以上仿真看出采用本章提到的基于ICA的去干扰算法可以成功地将干扰信号从混合信号中分离出来。说明此方法可以用来进行风机混合信号的预处理。

5 结 论

本文针对风力机组信号的非稳态特性，探讨了其噪声信号分离的盲处理手段，选用了基于基于EMD与ICA的盲分离方法，对混有强干扰信号的混合信号进行处理，分离出想要研究的微弱机械信号。最后设计仿真实验分析来验证了此方法的分离效果。