面向InSAR的空气扰动影响机翼挠曲变形建模
朱庄生,张萌
(1.北京航空航天大学 仪器科学与光电工程学院,北京100083; 2.惯性技术重点实验室,北京100083;3.新型惯性仪表与导航系统技术国防重点学科实验室,北京100083)
干涉合成孔径雷达(Interferometry Synthetic Aperture Radar,InSAR)是在合成孔径雷达(Synthetic Aperture Radar,SAR)二维成像基础上发展并逐渐成熟起来的三维遥感成像技术。InSAR技术中的相位干涉基于相位连续性假设,即要求任意相邻像素之间的绝对相位差小于π[1],因此双节点(即单基线)InSAR技术适用于地形平坦区域。为解决实际测绘中高度突变区域的相位干涉问题,多节点(即多基线)InSAR技术应运而生[2],垂直航向上基于多载荷节点构成的长短基线联合测量,可有效克服高度突变、噪声干扰等影响,现已成为航空遥感领域的主流发展方向。
受外部扰动的影响,InSAR载机成非理想运动,机翼也会产生变形和振动,进而导致InSAR系统各节点载荷处形成复杂运动,即引起干涉基线长度的变化。从相位干涉技术可知,干涉基线长度测量误差直接决定了InSAR的高程分辨率[3],目前主要借助传递对准技术并辅以机翼挠曲变形误差建模补偿技术[4-5]提高基线测量精度,机翼挠曲变形误差建模是其核心问题之一。
机翼挠曲变形误差建模方法主要有3类:
第1类是基于随机理论建模。该方法将机翼挠曲变形当作Markov模型[6]或AR模型[7],并将其增广为卡尔曼滤波状态量[8]或噪声量[9]进行估计。如Kain和Cloutier[8]设计的42维卡尔曼滤波器中有18个挠曲运动状态量,公式复杂,计算效率低。该方法局限性在于模型参数设定无实际依据,也未考虑外界干扰变化对机翼变形的影响分析。
第2类是直接测量法。如摄影测量法,其要求摄影机对测点通视或直视,主要用于航天领域,如美国的SRTM[10](Shuttle Radar Topography Mission)。在航空领域,由于机翼变形过大或天气影响,摄影机对测点难以保证直视或通视。如基于光纤光栅(Fiber Bragg Grating,FBG)传感器的机翼变形测量,借助FBG感知应变信息,计算机翼变形,多应用在机翼健康监测[11]方面。
第3类是基于有限元仿真的变形建模。有限元仿真是基于计算流体力学(Computational Fluid Dynamics,CFD)及计算结构力学(Computational Structural Mechanics,CSM)的流固耦合理论发展起来的,其湍流模型成熟、可控性强,主要应用于计算飞机气弹性力和结构响应[12]及安全设计[13]。如陈志敏等[14]利用有限元仿真获得机翼受气动载荷作用的弯曲和扭转变形情况;张华等[15]利用Nastran软件分析大展弦比复合材料前掠机翼和后掠机翼在气动载荷作用下的静气弹变形情况。
机翼挠曲变形主要源于内部扰动(如发动机振动、机翼结构及材料等)和外部扰动(如空气扰动等)的影响,内部扰动随着飞行平台的确定可认为是一些已知量,而外部扰动是一个复杂的过程。本文利用有限元软件针对空气扰动对机翼结构的气动力影响与结构响应进行仿真求解,建立起空气扰动影响下的机翼挠曲变形模型,并借助应变估计位移的模态叠加原理对模型进行验证计算。
1 空气扰动类型及影响因素分析
1.1 空气扰动的复杂多源性
对于机载多基线InSAR系统,具体结构如图1所示,DLR研制的E-SAR[16]工作高度为3~5 km,NASA研制的AIRSAR[17]和TOPSAR[18]分别工作在8 km和9 km高度;中国科学院电子学研究所研制的机载三基线InSAR[19]工作在3 km航高上,该所研制的MiNiSAR[20]工作在0.5~3 km高度。综上,本文考虑机载InSAR系统成像高度范围为0.5~9 km,在此工作区域内的空气扰动主要为垂直风切变、阵风及大气湍流[21]。

图1 机载分布式InSAR系统Fig.1 Airborne distributed InSAR system
1.1.1 垂直风切变
垂直风切变指的是垂直气层任意两观测点之间风向和风速的突然变化,计算公式为

式中:S2、S1分别为空间A、B两点的风速值。
根据GJB 5601—2006[22]给出的垂直风强度,计算H=30、50、70、100m工作高度突变所引起的风切变大小,如图2所示。
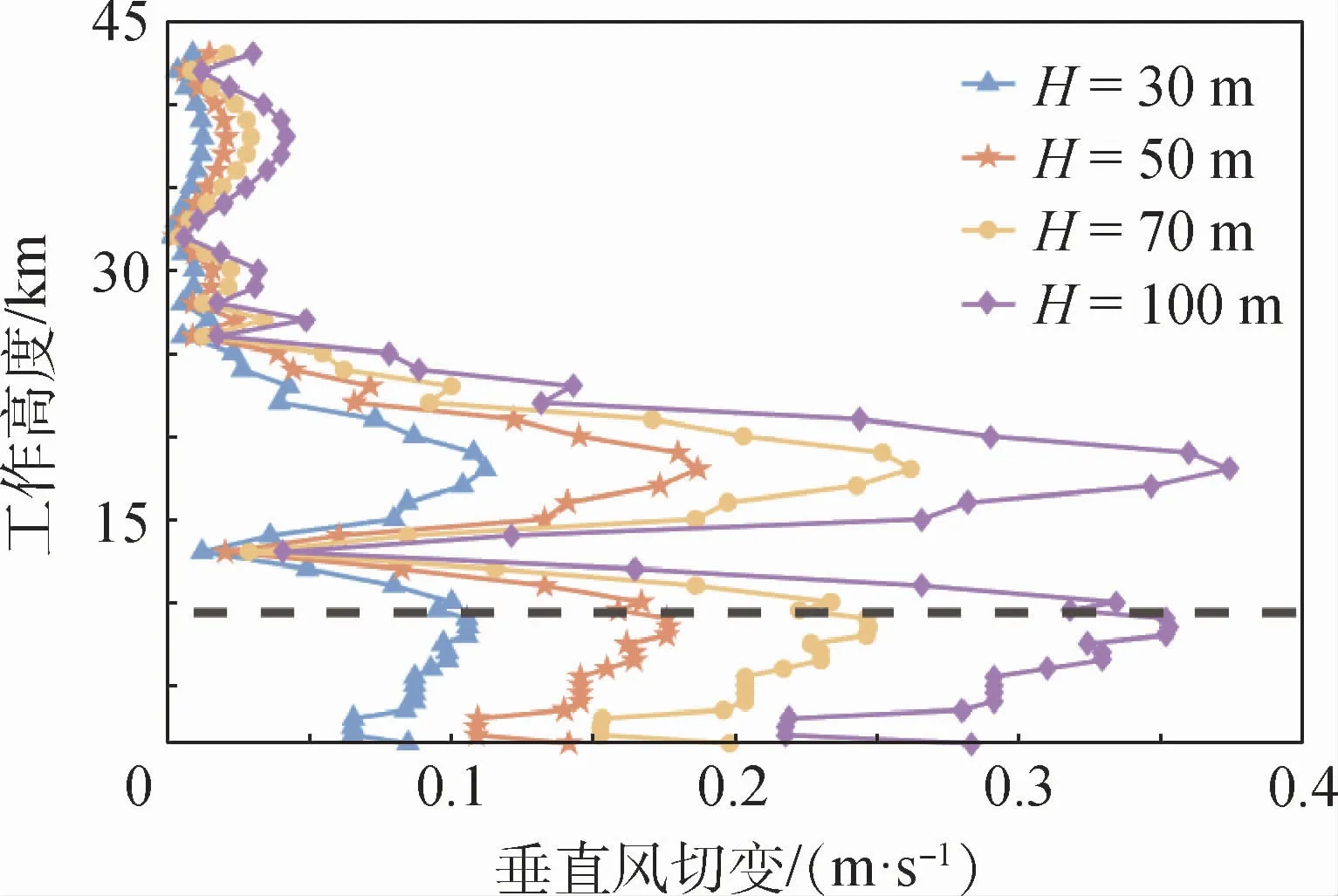
图2 不同高度变化引起的垂直风切变Fig.2 Vertical wind shear caused by different height changes
由图2可知,在10 km的工作高度内,100 m的高度变化最大可引起0.35m/s的垂直风切变;航空中经常取30m的高度变化判断其对飞行器的影响[23],本文计算可得垂直风切变大小为0.1m/s;根据国际民航组织规定垂直风切变小于1m/s的情况下与风切变强度小于0.033/s的风切变等级为微弱影响[23]。除此之外,由于垂直风切变影响载机升力最终改变载机工作高度,需控制载机产生相反的工作高度变化,如垂直风切变引起工作高度下降,则需提高当前工作速度以产生更大升力来提高载机的工作高度;而起飞和降落阶段的工作速度小,机动余量小,改变工作高度又不够,通常认为垂直风切变主要影响起飞和降落阶段[24]。

1.2.1 仿真条件设置
建立如图4所示的机翼蒙皮骨架结构。蒙皮厚度为2mm,骨架结构由翼梁、翼肋和桁条组成,图4中从左端0.1m处起每隔0.2m分别为测点1~测点15;采用BOEING103翼型,翼弦为0.6m,总长为3m,材料为铝合金7075,材料属性如表1所示。
基于有限元软件ANSYSWorkbench分析载机工作速度、高度引起的大气湍流变化对机翼变形量的影响,主要利用ICEM CFD软件、Fluent模块及Static Structural模块进行流固耦合求解。应用ICEM CFD软件建立如图5所示的机翼飞行流场网格区域,分为壁面区域、湍流入口区域、湍流出口区域及机翼结构。在Fluent模块中计算机翼不同工作状态下所受的气动载荷,湍流模型采用单方程Spalart-All maras模型;气体设置为constant,不同工作高度上的气体密度根据表2[22]确定;边界条件采用速度入口、压力出口条件,压力、温度根据表2[22]确定。在Static Structural模块中将Fluent计算载荷施加在机翼上,计算机翼结构应变及变形。
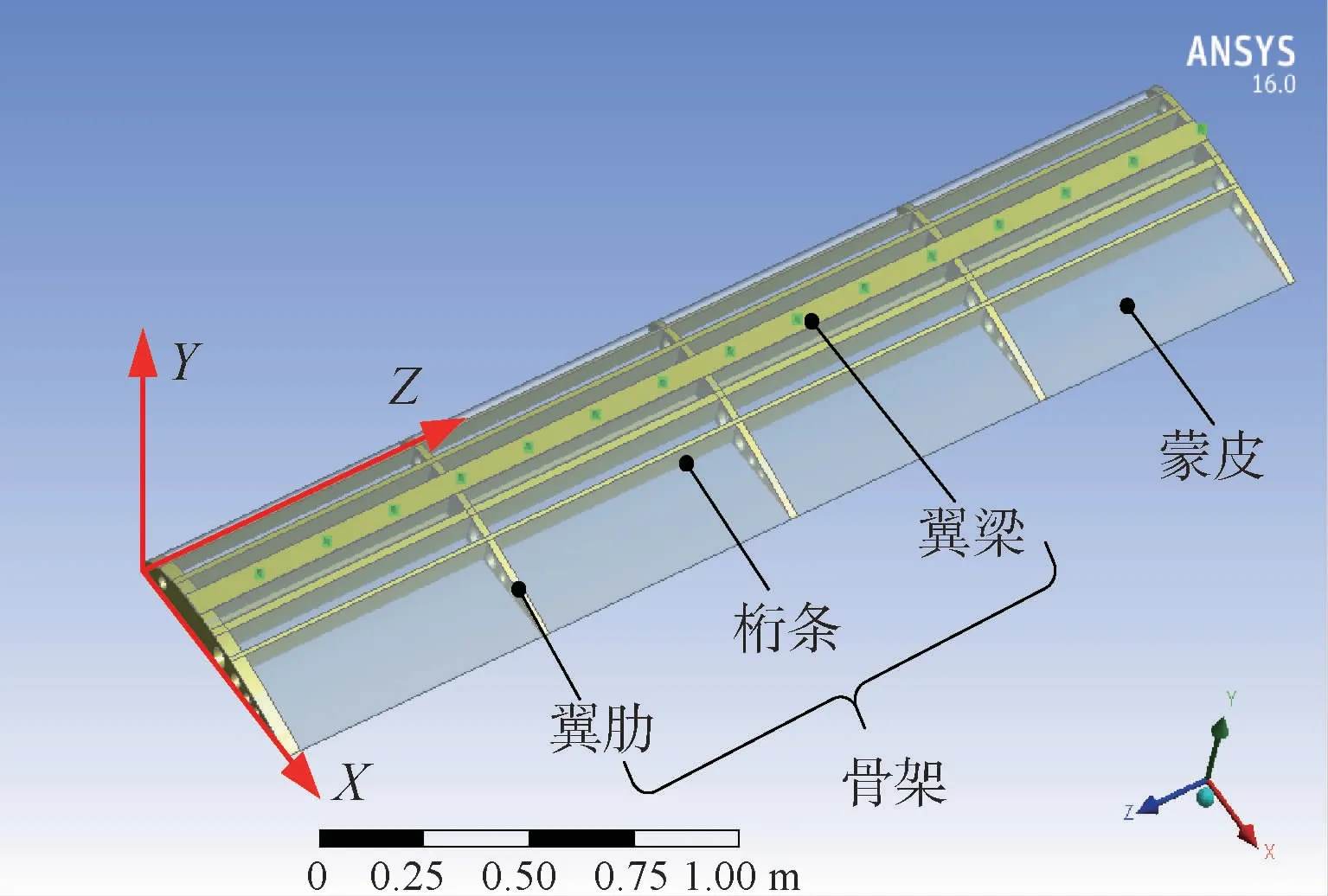
图4 机翼模型Fig.4 W ing model

表1 铝合金7075材料属性Table 1 A luminum alloy 7075 m aterial p roperties
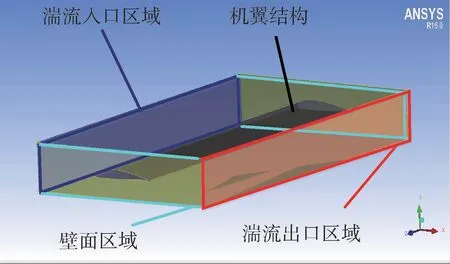
图5 机翼飞行流场区域Fig.5 W ing flight flow field area
以载机工作高度3 km、速度200 m/s为例,Fluent计算蒙皮气动载荷及湍流速度变化,如图6所示,Static Structural计算骨架结构Y向(横向)位移,如图7所示,图7中左端至右端的变化表示机翼变形量的增大。
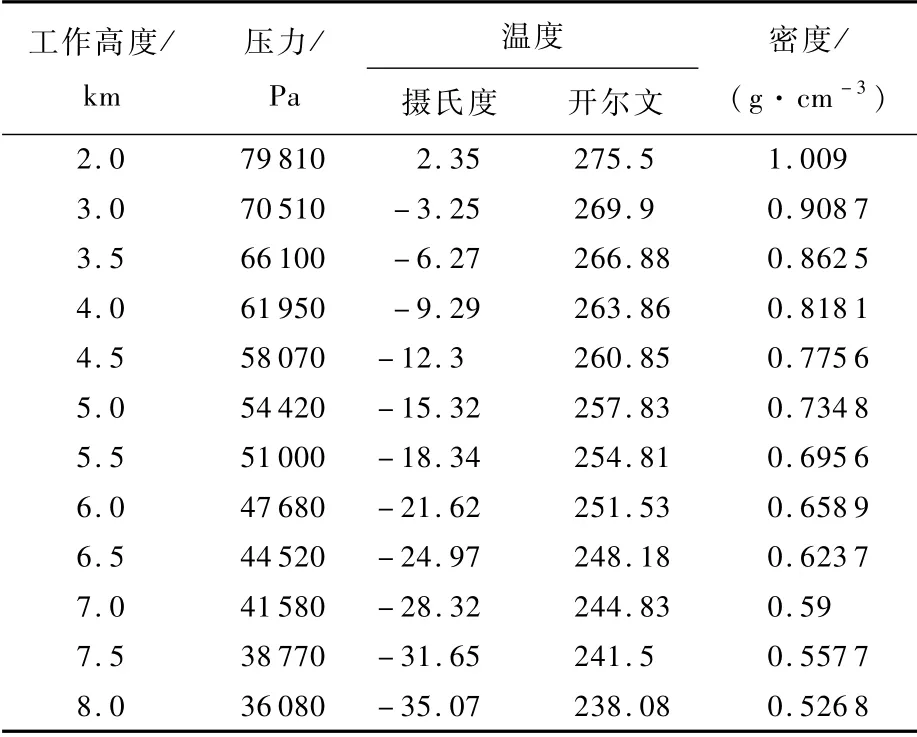
表2 不同工作高度上的大气物理参数[22]Table 2 Atmospheric physical parameters at different working altitudes[22]
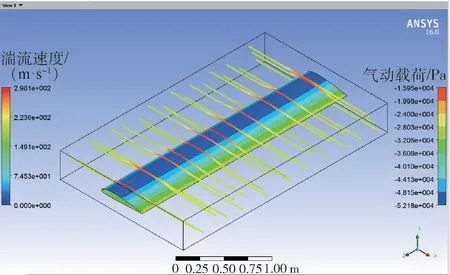
图6 机翼所受气动载荷及湍流速度变化Fig.6 Changes in aerodynamic loads and turbulent velocity on wing
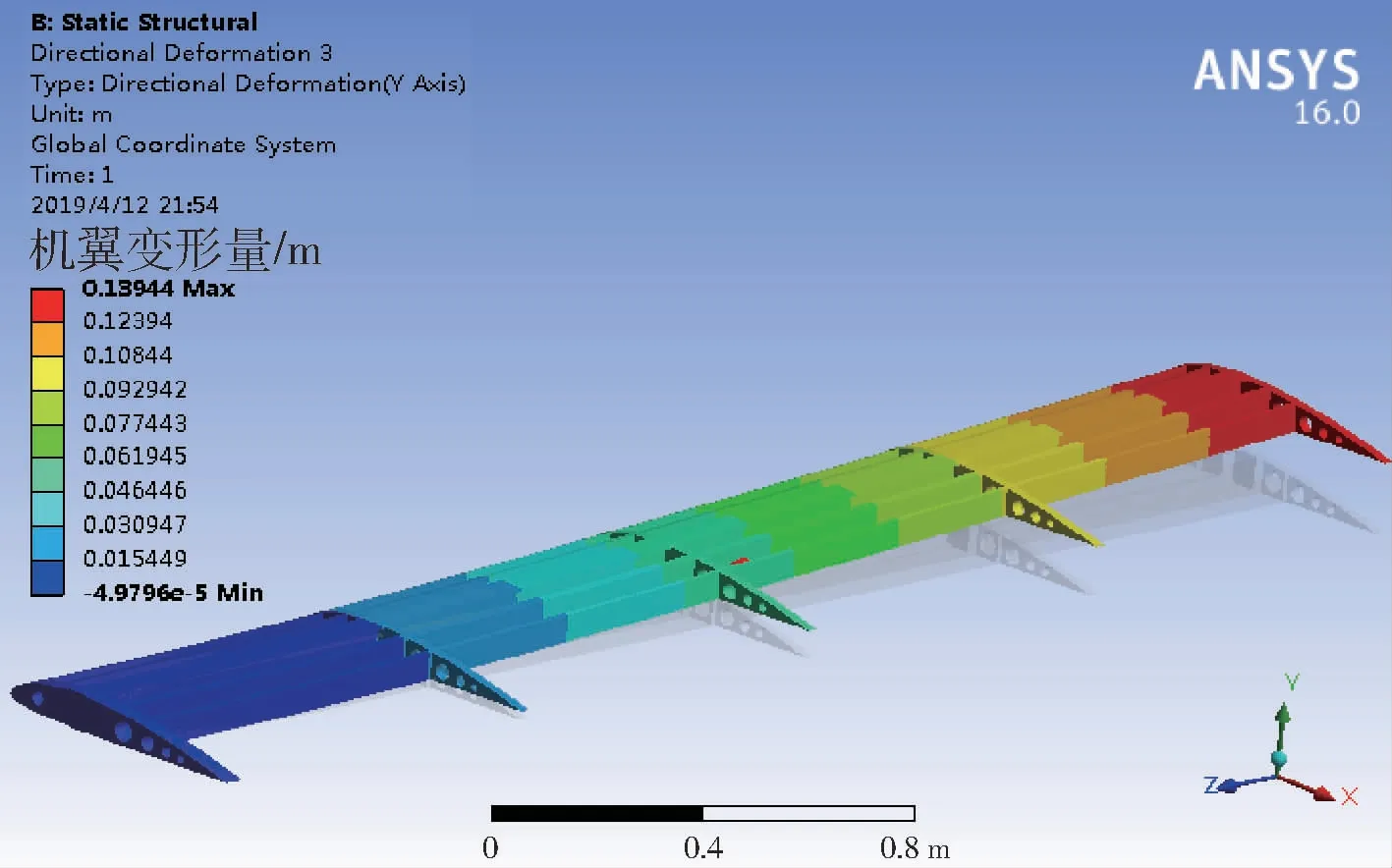
图7 机翼结构Y向位移Fig.7 Y-direction displacement of wing structure
1.2.2 大气湍流影响机翼挠曲变形仿真分析
载机工作高度一定时,即大气密度、压力、温度均未变化时,仅仅是工作速度变化影响大气湍流,仿真3 km航高上150 m/s起每隔5 m/s直至250m/s的工作速度下大气湍流对机翼挠曲变形的影响,结果如图8所示。
为分析航空遥感系统工作高度对机翼变形量的影响,采用载机从2.5 km 起每隔0.5 km 到6 km的工作高度变化,以及从125 m/s起每隔25m/s到300m/s的工作速度变化来获取仿真数据,具体的湍流参数按照表2设置。在此仅列出测点15的位移,如图9所示。
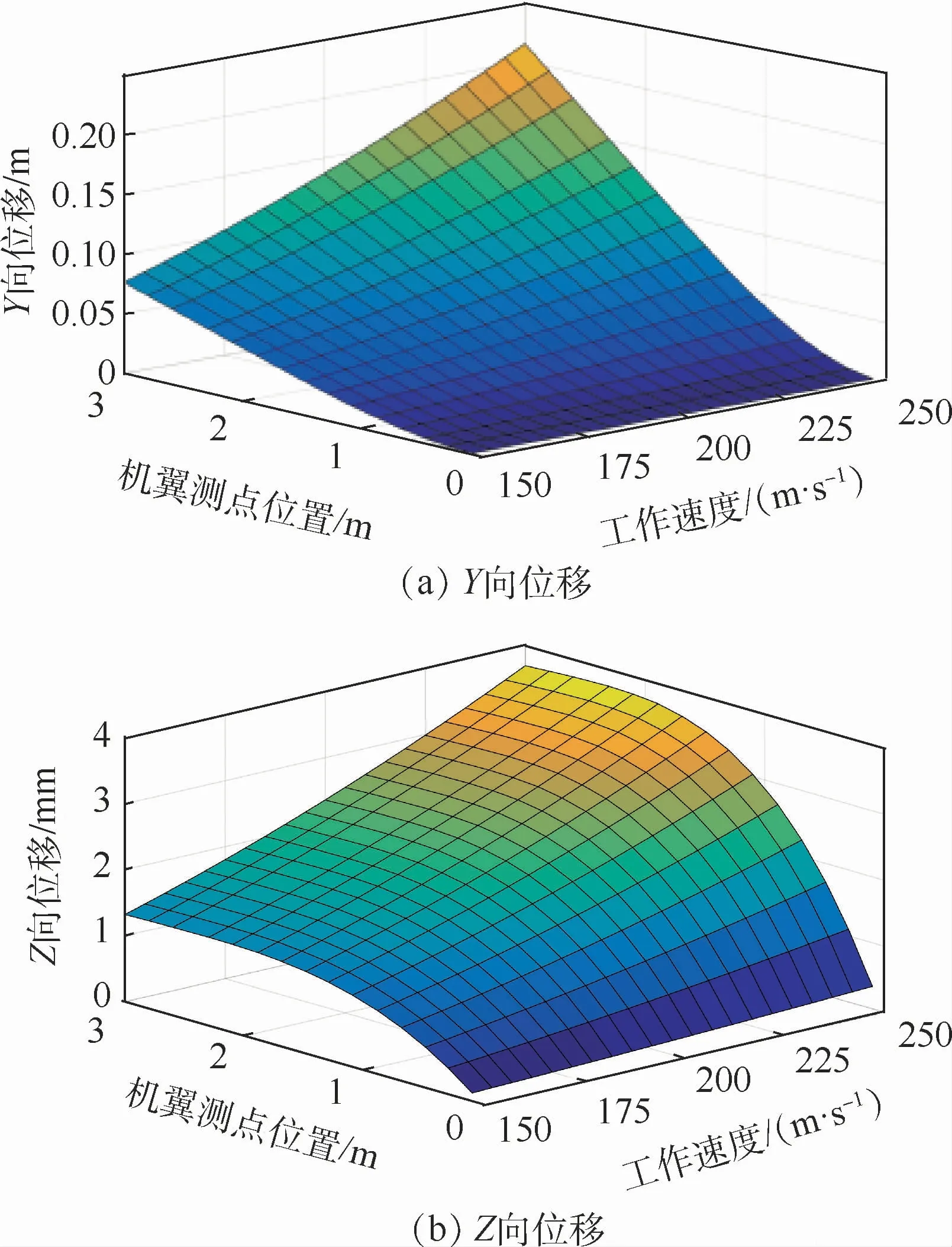
图8 不同工作速度时的机翼挠曲变形Fig.8 Deflection of wing at different working speeds
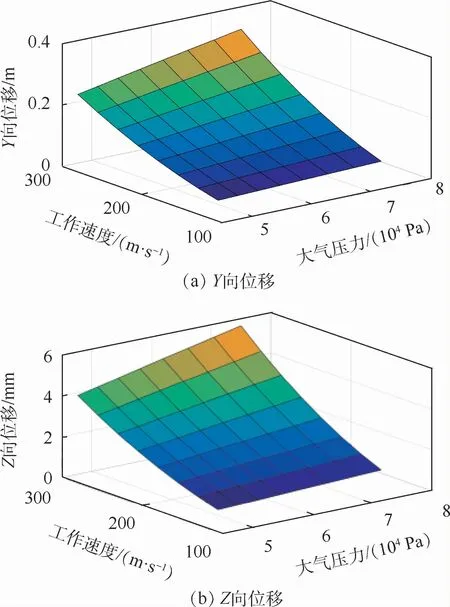
图9 不同工况下测点15的机翼挠曲变形Fig.9 Wing deflection deformation atmeasuring point 15 under different conditions
可以看出,随着工作高度递增(压力减小),位移量逐渐减小且近似一阶线性关系;综合图8可看出,位移量随工作速度变化近似二阶关系。下文将借助机翼受力变形模型并结合实验数据来分析大气湍流对机翼挠曲变形的影响。
2 模型建立及参数辨识
2.1 大气湍流影响机翼挠曲变形模型建立
InSAR载机的工作速度、高度变化将引起大气湍流变化,由于湍流在飞行中测量难度较大,所以本文将InSAR载机的工作速度、高度作为输入量,大气湍流作为未知中间量,机翼变形量作为输出量,建立起载机不同工作速度、高度影响下的机翼挠曲变形模型。
变形建模主要有机理建模法和测试分析法。机理建模法根据对象特性分析其因果关系寻找内部机理,所建模型具有物理数学意义。如詹斌[31]通过分析石墨烯纳米金属基复合材料的变形机理建立起其塑性变形模型。该方法一般基于大量简化及假设前提,难度较大,不具有普适性。测试分析法又称参数辨识法[32],是将研究对象特性视为“黑箱”,只能利用大量表征系统规律和状态的实验数据,运用统计方法建立与原始数据拟合度最好的模型,所建模型在线校正能力强;该方法无需了解系统机理,但需设计合理实验以获得系统最大信息量。所以,通常采用机理分析结合参数辨识法[33]建立模型。如关永亮[34]基于复合材料变形机理综合参数辨识法建立起复合材料机翼的非线性动力学变形模型。
对于本文建立机翼挠曲变形模型而言,首先需要明确大气湍流与其引起的机翼所受载荷之间的关系,其次需要明确机翼载荷与机翼挠曲变形之间的关系,从而初步建立起机翼挠曲变形机理模型,最后通过获取的仿真实验数据对模型进行参数辨识并建立模型。
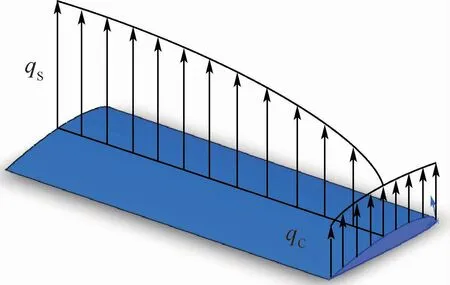
图10 蒙皮表面气动载荷分布Fig.10 Aerodynamic load distribution on skin surface
对于图4所示的机翼结构,蒙皮感受如图10所示的沿翼展分布载荷qS、翼弦分布载荷和qC,为飞机提供升力并将外载荷传递给骨架,并不是主要的承力结构。对于骨架结构而言,桁条对蒙皮起支撑作用,并承受由蒙皮传递的气动载荷;翼肋保持机翼的气动外形并承受一定剪力;翼梁在根部与机身相连,主要承受机翼的弯矩和剪力[35],并且多节点InSAR成像载荷主要分布在翼梁上。综上,考虑骨架整体结构承受机翼的弯矩和剪力,即InSAR基线长度误差将直接取决于机翼骨架结构的挠曲变形建模误差[3]。
实际情况下,翼梁结构与机身相连,形成一个悬臂梁的状态,本文对于骨架整体结构也是基于悬臂梁假设考虑的,受力变形情况如图11所示。
2009年,美籍华裔科学家高锟获得诺贝尔物理学奖,然而在得到自己摘取“科学王冠上的明珠”的消息时,高锟的阿尔茨海默病病情已经非常严重:他不能理解自己为何被称为“光纤之父”,也不知道诺贝尔奖是一个科学家所能够获得的最高荣誉。
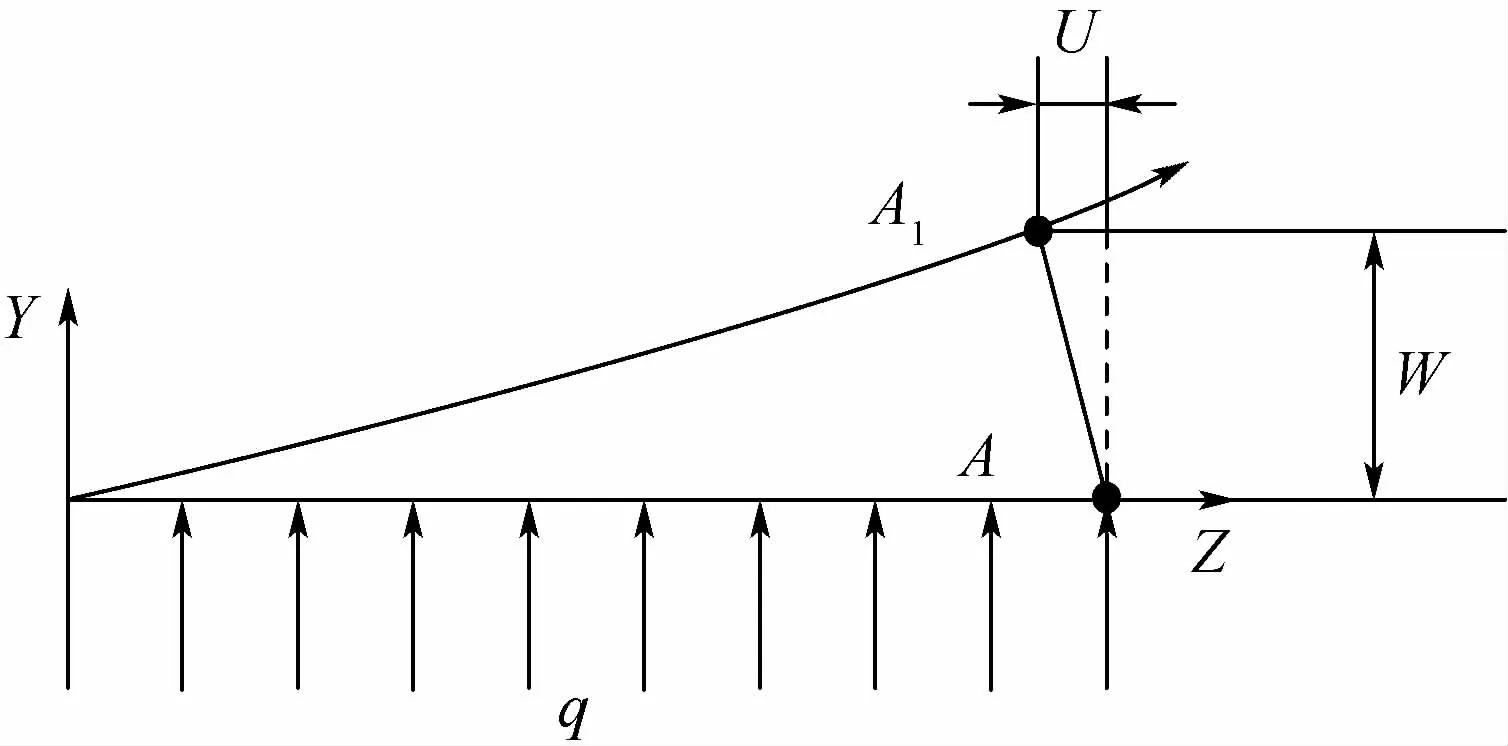
图11 机翼骨架结构变形示意图Fig.11 Schematic diagram of wing skeleton structure deformation
文献[36]给出了悬臂梁在载荷q作用下与其产生的横向弯曲位移(挠度)W之间的关系:

式中:pw(z)=[(l-z)4+4l3z-l4]/(24EI),l为悬臂梁长度;z为距固定端距离;E为弹性模量;I为截面惯性矩。
根据梁的弯曲理论,距中性层距离d处的轴向位移U与该截面处挠度W的关系为:U(z,h)=将式(4)代入计算可得设轴向位移为

已知机翼蒙皮感受载荷qL、qD,以及载荷作用下机翼变形量W、U,并根据式(1)可确定载机工作速度影响湍流速度。综上,初步建立起载机工作速度引起大气湍流的变化所影响的机翼挠曲变形模型为


式中:AY、AZ项随机翼位置变化,与机翼材料、尺寸及气动性能有关;vB体现骨架感受气动载荷的大小,B为一常值,不随机翼位置变化,表示载机工作速度、湍流速度对载荷的影响。由机翼受力变形机理建立模型式(6)、式(7),借助实验数据辨识模型参数可建立起载机工作速度影响机翼挠曲变形模型;而工作高度影响湍流尺度、强度机理复杂,只能借助参数辨识法建立。
2.2 基于回归分析的参数辨识
基于参数辨识法建立机翼挠曲变形模型的方法主要有时序分析法和回归分析法。时序分析法是对实验数据基于ARMA模型、AR模型、MA模型等研究分析、识别参数。如解春明等[7]将机翼挠曲变形当作AR模型,并利用卡尔曼滤波对其进行在线补偿。该方法的局限性在于验证数据的平稳有序性,重点是模型阶次n的选择,即考虑前n时刻对当前时刻的影响。对本文建立载机工作高度与速度影响机翼挠曲变形的模型而言,并不适用。
本文建立载机工作速度与高度自变量与机翼挠曲变形因变量之间的数学关系,与利用回归分析辨识参数的理论思想相契合,所以基于回归分析法借助有限元仿真实验数据对机翼挠曲变形机理模型辨识参数。
回归分析中,常用线性回归模型:LR(xm)=Am1xm+Am2;非线性回归模型:指数函数等。利用回归分析可对同一组数据拟合出多种不同模型,常用相关指数R2及残差平方和SSE选择最优拟合模型,SSE越小及R2越接近1,说明实际数据与预测值越相近,拟合程度就越好。
根据上述分析,对于载机工作速度影响下的机翼挠曲变形模型,直接利用非线性模型中的辨识参数建立模型;对于工作高度变化所引起的大气湍流影响下的机翼挠曲变形模型,利用上述回归模型进行拟合处理,选择与原始实验数据拟合程度最好的模型进行下一步的计算及预测。
2.3 大气湍流影响载机挠曲变形模型建立
对于3 km工作高度上载机工作速度变化的实验数据,借助幂函数u=AvB辨识参数建立起载机工作速度影响机翼挠曲变形模型,在此列出机翼骨架结构上测点2、测点7、测点12、测点15的Y向位移数据依据u=AvB的参数辨识结果,如表3所示。
对比表3中3个不同拟合模型,根据SSE越小和R2越接近1的判断准则选择最优拟合模型,确定InSAR载机在3 km工作高度上工作速度从150m/s变化至250m/s的情况下,Y向、Z向机翼变形量满足:

式中:AY、AZ项与机翼测点位置、机翼结构的材料、尺寸及气动性能有关;v2.015项体现载机工作速度和湍流速度与机翼承受载荷间的关系。
对于建立工作高度影响机翼挠曲变形模型而言,高度仅仅体现压力、温度和密度的变化,所以该模型转换为容易测量获取的不同工作高度上所对应的压力值与机翼变形量之间的关系。对同一工作高度2.5~6 km上载机工作速度变化引起的机翼变形数据进行处理,发现均满足式(8)和式(9),仅系数AY、AZ发生变化,变化趋势如图12所示。可以看出,AY、AZ随高度变化趋势保持一致且近似一阶关系,与距固定端距离z关系近似三阶关系。
选择测点2、测点7、测点12、测点15的Y向位移进行参数辨识,统计结果如表4所示。
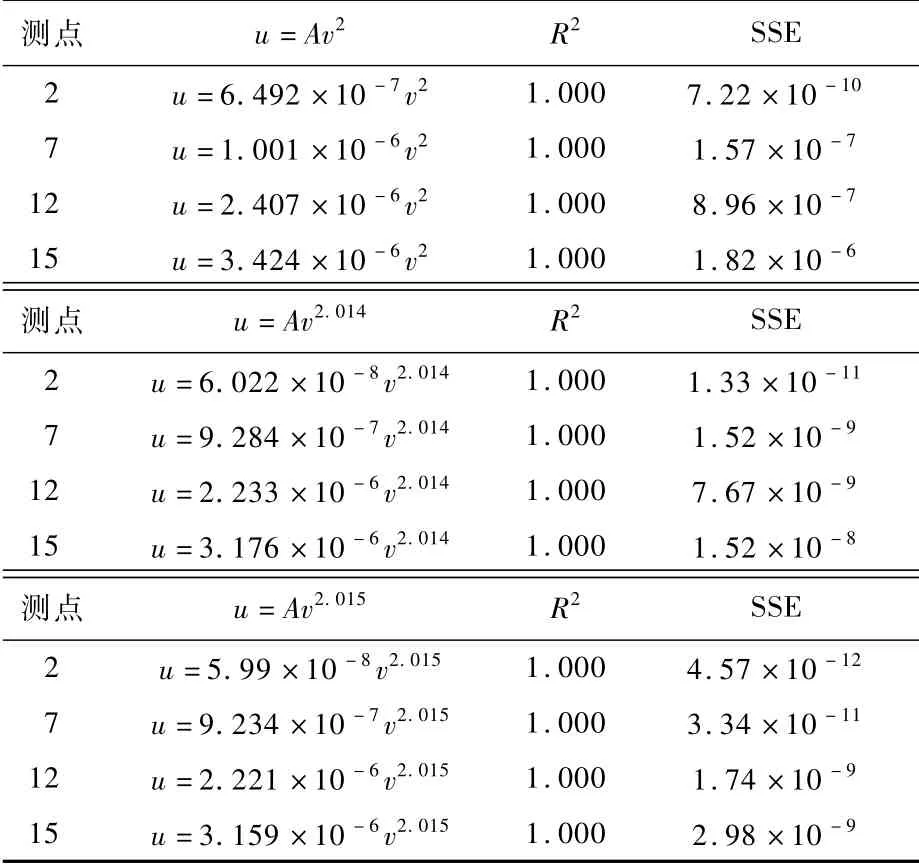
表3 载机工作速度影响的参数辨识结果Table 3 Parameter iden tification results of carrier speed
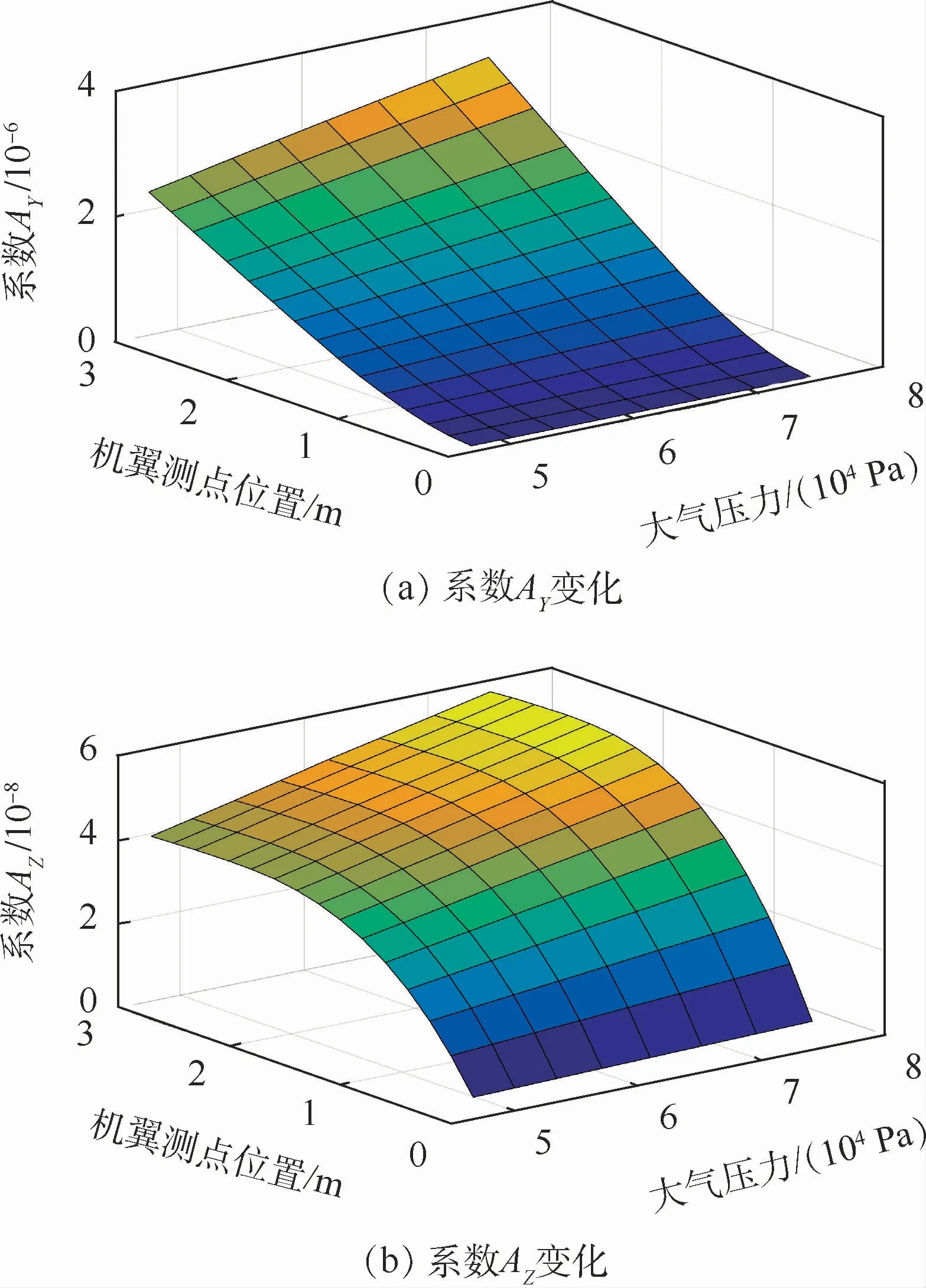
图12 高度变化时的AY、AZ 系数Fig.12 AY and AZ at different heights
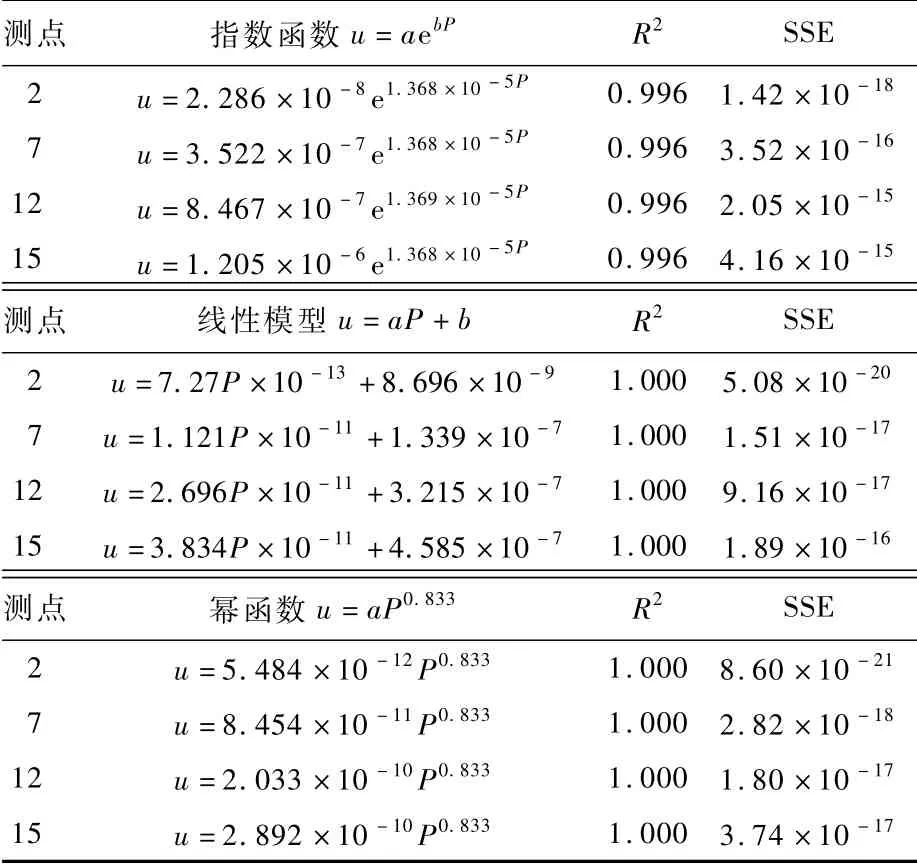
表4 载机工作高度影响的参数辨识结果Table 4 Parameter identification results of car rier’s work ing height
对比表4中模型,根据SSE越小及R2越接近1的判断准则,确定工作高度变化时系数AY、AZ满足:
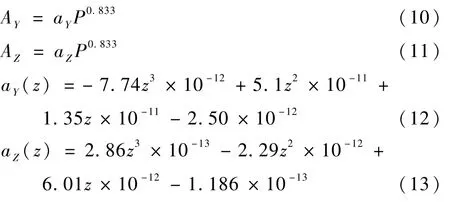
式中:aY、aZ随机翼结构及测点位置z变化;P表示不同工作高度上的压力。
综上,载机工作高度以及工作速度影响机翼挠曲变形模型可表示为

式中:P、v项为与机翼载荷大小相关量。
3 仿真实验
3.1 基于建立模型的机翼挠曲变形误差仿真分析
利用式(14)、式(15),对于不工作高度、不同工作速度下变形数据进行预测计算,表5和表6列出了测点7、测点12、测点15的变形数据。
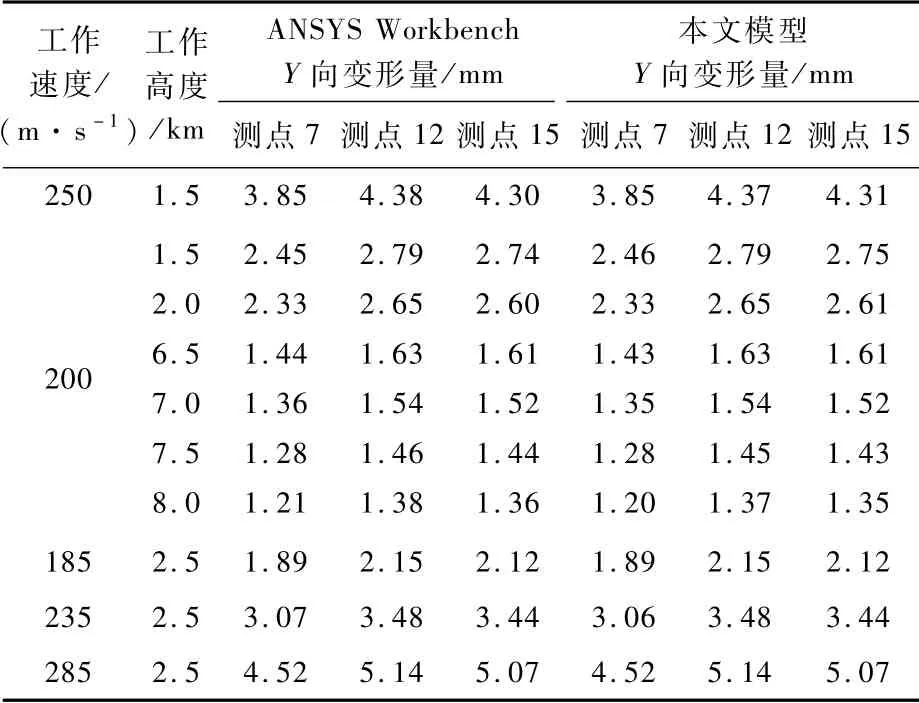
表5 本文模型预测Y向变形Table 5 Y-direction deform ation pred icted by p roposed model
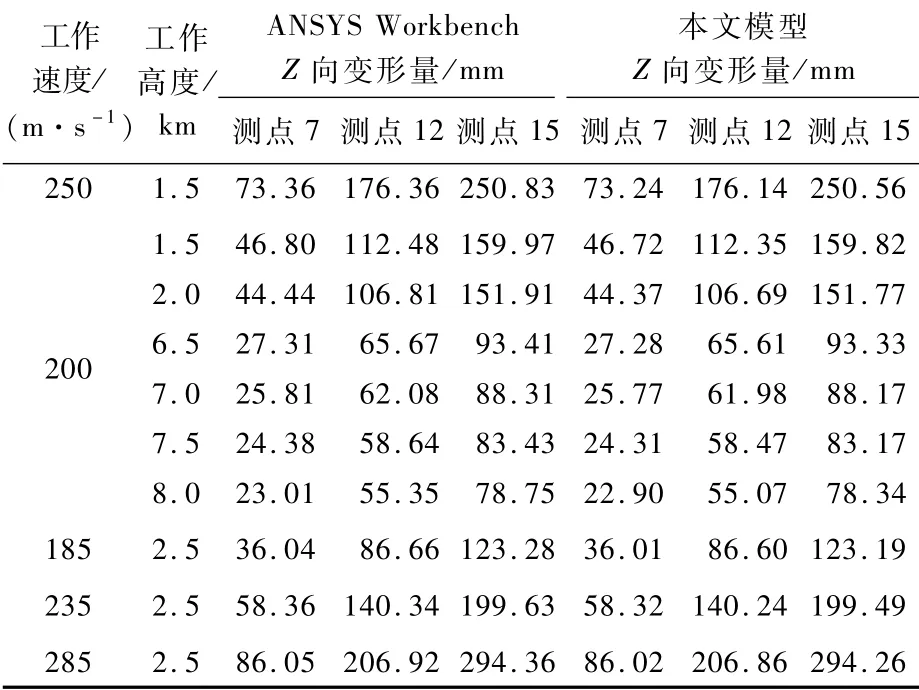
表6 本文模型预测Z向变形Table 6 Z-direction deform ation pred icted by p roposed model
3.2 基于模态叠加原理的机翼挠曲变形误差仿真分析
对于本文所建模型,适用于已知InSAR载机工作速度、高度的机翼挠曲变形量的计算,本文借助模态叠加原理(又称模态法)对其适用性及精度进行验证。模态叠加原理[38]基于载荷作用下结构应变响应估计位移,存在:

式中:D为待估计位移值;S为测点应变值;DST为应变、位移转换矩阵,轴向位移矩阵DST u=[фu]([ψu]T[ψu])-1[ψu]T,横向位移矩阵DSTω=[фω]([ψu]T[ψu])-1[ψu]T,[фu]、[ψu]和[фω]分别为轴向应变、位移和横向位移矩阵。

图13 骨架结构的应变、位移模态Fig.13 Skeleton structure strain and displacementmode
利用ANSYSWorkbench模态分析可获得骨架结构的应变、位移模态,如图13所示。基于仿真分析最终计算出DST矩阵。将仿真获取的应变值利用式(16)便可估计Y向、Z向位移。表7和表8列出了不同飞行条件下测点7、测点12、测点15利用模态叠加原理的计算结果。
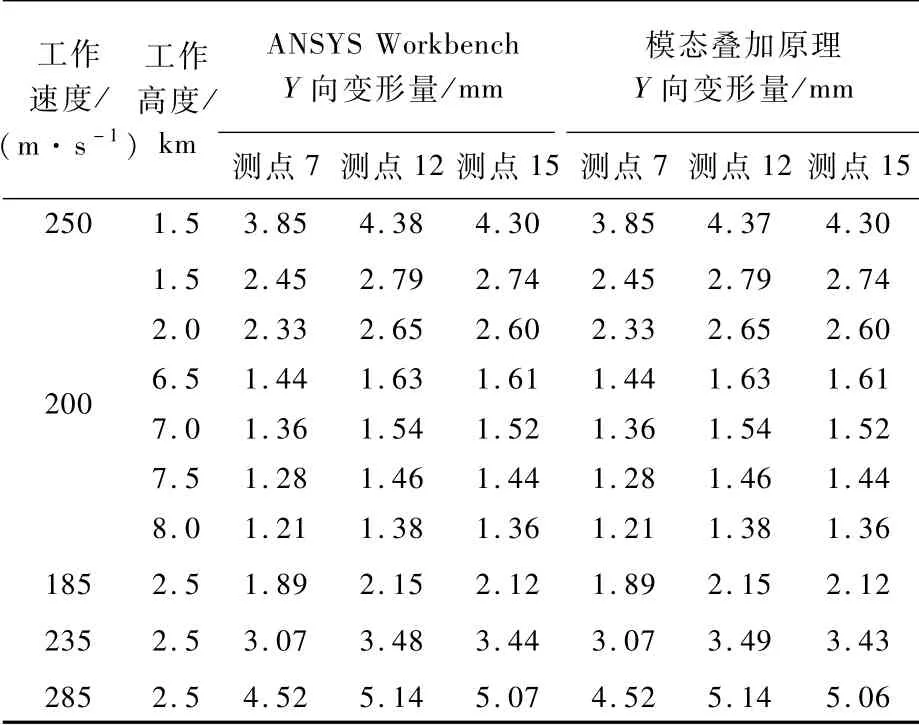
表7 Y向变形模态叠加原理计算结果Table 7 Y-d irection deform ation calcu lated by modal superposition principle
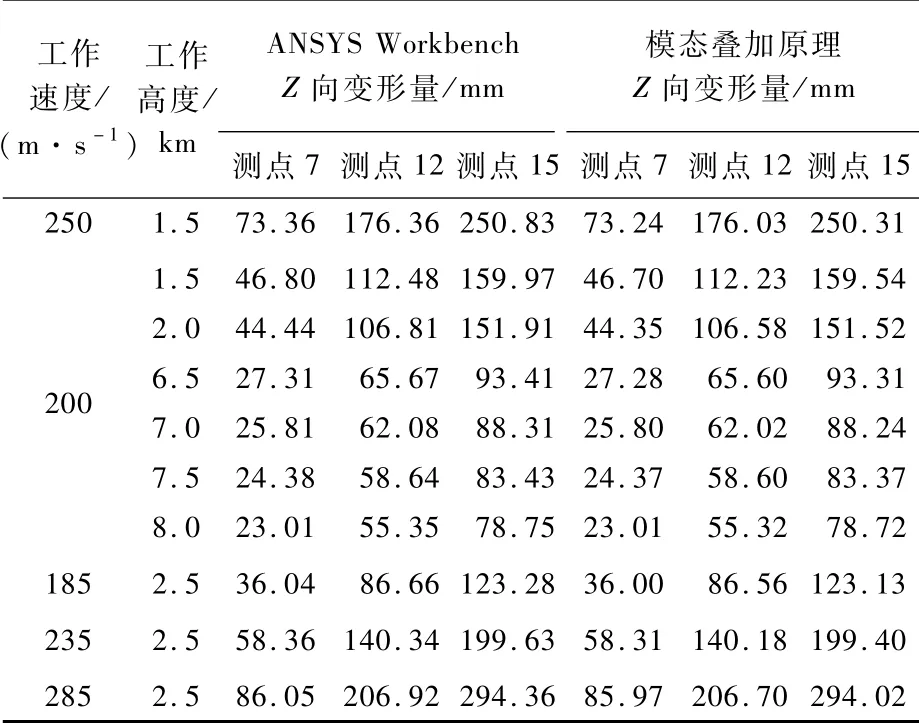
表8 Z向变形模态叠加原理计算结果Table 8 Z-d irection deform ation calcu lated by modal superposition p rinciple
3.3 仿真结果及分析
从表5~表8可知,利用本文模型及模态叠加原理计算Y向、Z向位移与ANAYS仿真有一定误差。表9列出了2种方法的计算误差。
从表9可以看出,利用模态叠加原理及参数辨识建立模型计算横向最大误差均在0.6mm以内,轴向最大误差均在0.015mm以内,即利用模态叠加原理与回归预测2种方法均能很好地估计出Y向、Z向位移量,既验证了本文方法的可行性,又对比了2种方法的计算精度。
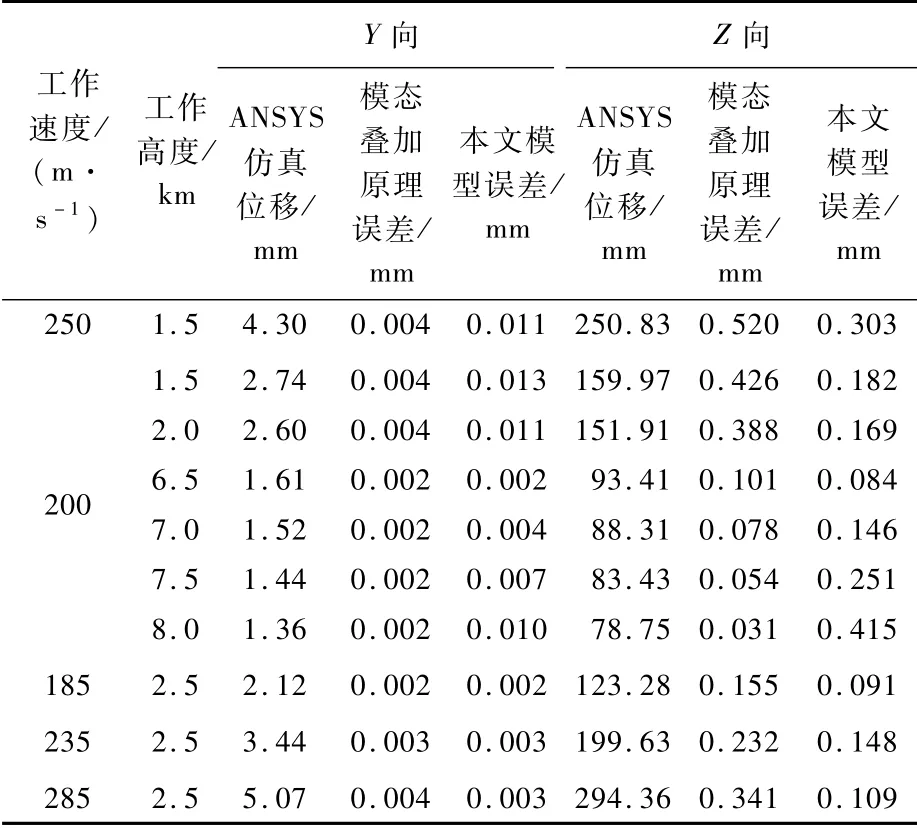
表9 本文模型与模态叠加原理计算误差值对比Table 9 Com parison of error values calculated by p roposed model and modal superposition p rinciple
4 实测实验
4.1 实验系统及步骤
为验证本文方法,搭建起如图14所示的机翼结构分布式光纤光栅测量系统,将InSAR载机在不同大气湍流情况下所承受气动载荷转换为对机翼结构施加不同加载量。以0.5 kg每隔0.5~5 kg的加载量代表3 km工作高度上150m/s起每隔10m/s直至240m/s工作速度的机翼所受载荷;仿真实验中不同湍流扰动下的机翼变形量由ANSYS直接计算获取,本节实验利用光纤光栅传感器实时获取其变形量;由此建立起湍流扰动模拟加载量与机翼变形量之间的映射关系,从而进行预测计算。

图14 实验室机翼结构Fig.14 W ing structure in laboratory
在机翼结构上进行加载实验,如图15所示,在实验过程中从0.5 kg开始,每次以0.5 kg的重量递增直到5 kg,每次加载保持静止状态5min以上,利用光纤光栅测量加载过程中的应变变化及双全站仪测量系统测量2个靶标测点的位移量。

图15 机翼加载实验Fig.15 Loading experiment in wing
4.2 实验结果及分析
对悬臂梁进行10次加载,全站仪测量2个靶标点的位移量如表10所示。
利用光纤光栅测量应变量并借助模态叠加原理计算可得加载过程当中的位移变化,并利用前7次加载基于模态值进行非线性回归分析建立模型,拟合值如图16所示。预测计算在机翼上施加39.2、44.1、49 N的位移值,与全站仪测量值进行对比计算,结果如表11所示。
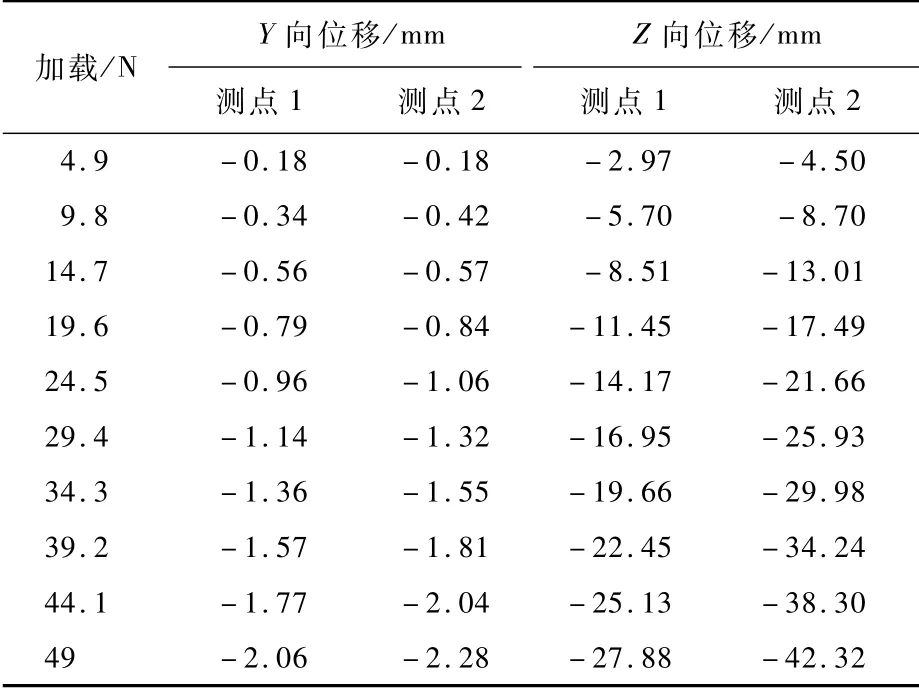
表10 全站仪测量值Table 10 Total station measurement values
从表11可以看出,利用模态值与全站仪测量值对比,Y向、Z向误差均在0.35 mm以内,既验证了本文方法的可行性,又验证了光纤光栅测量机翼挠曲变形的精度。
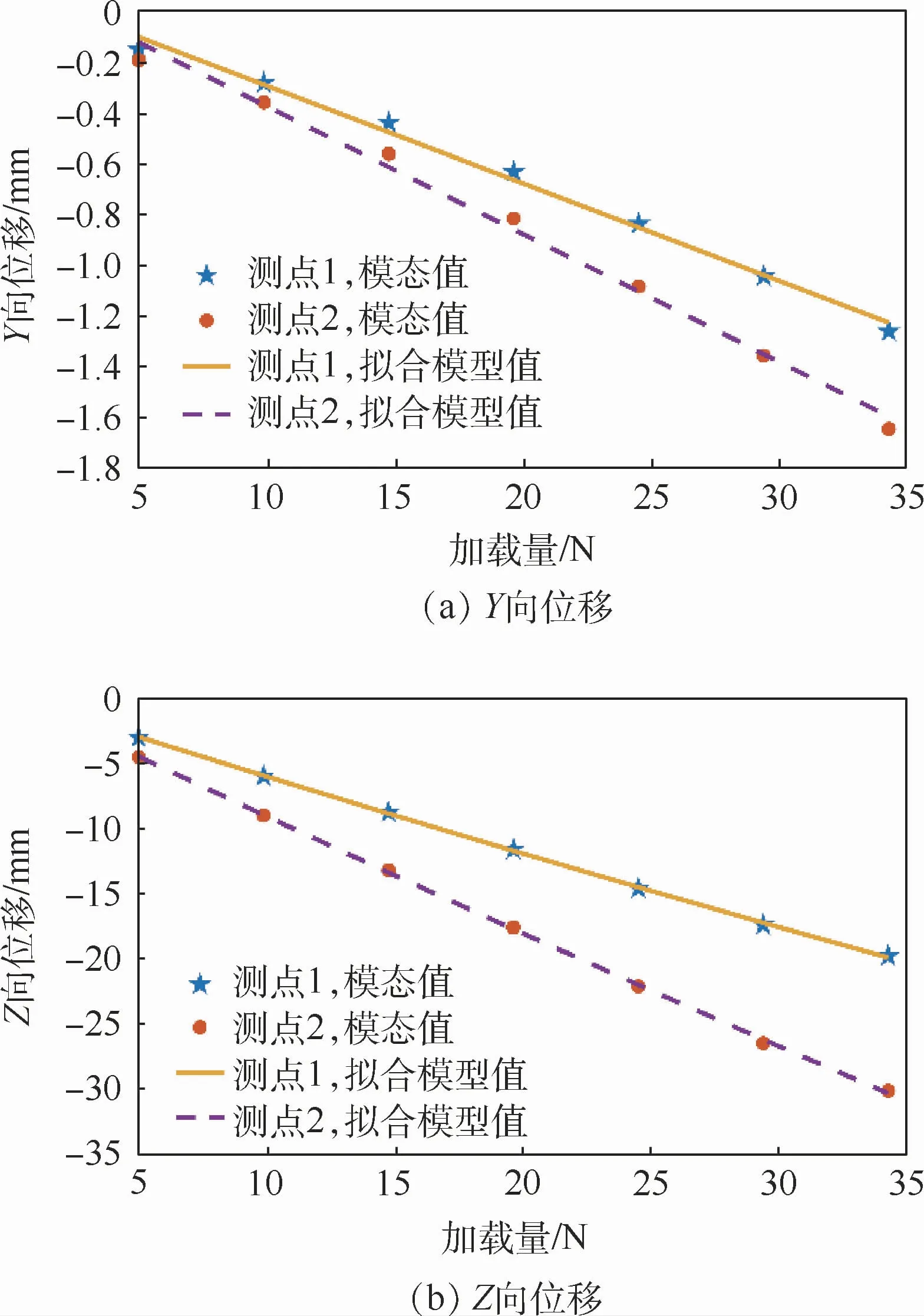
图16 模态值与拟合模型值对比Fig.16 Comparison of modal and fitted values
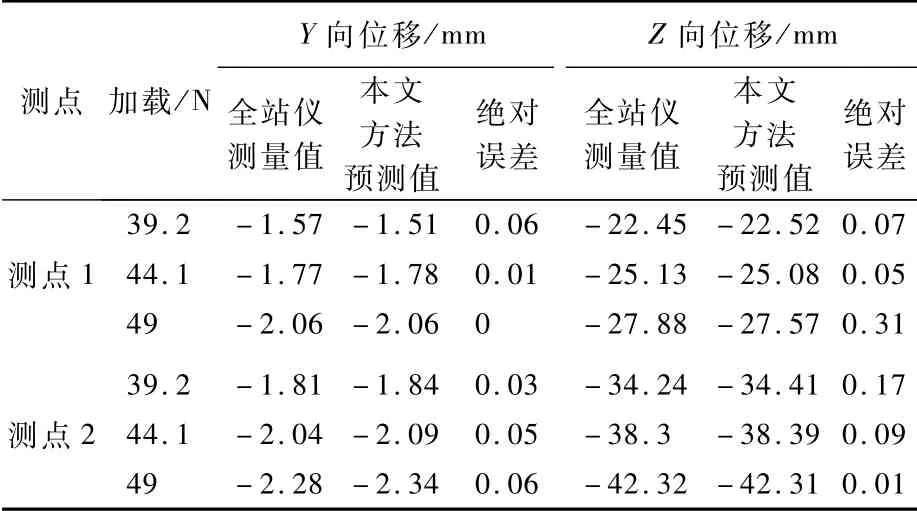
表11 预测值与全站仪测量值对比Table 11 Com parison of p redicted and total station measurement values
5 结 论
本文通过仿真分析了大气湍流对多节点In-SAR系统的载机机翼挠曲变形的影响,提出了一种基于机理建模综合参数辨识方法建立湍流影响机翼挠曲变形模型的方法,利用基于模态叠加原理的结构变形估计方法对其进行验证计算,并在实验室搭建起机翼挠曲变形测量系统对本文方法进行实验验证。
1)对不同工作高度、速度下的大气湍流仿真实验,构建了影响大气湍流因素与机翼结构挠曲变形之间的数学关系,从而实现将湍流对机翼挠曲变形的影响量化并建模分析以及预测。
2)与传统的大气湍流对于机翼挠曲变形影响的随机理论建模分析相比,本文方法借助大量仿真实验数据作为计算基础,提高了所建模型的可靠性。
本文的主要目的是基于工作高度、速度量测量来构建大气湍流与机翼挠曲变形量间的映射关系,其研究思路和研究方法对所有机翼结构具有普适性和推广性。但是,针对不同机翼结构,其升力、阻力等相关系数不同,以及在同等外力条件下,机翼变形量也不同;所以,针对不同的机翼结构本文所建模型系数应有所调整,这也是后续的重点研究工作。

