求解一类随机Hamilton系统的分裂算法

李鑫宇, 陈旭梅, 岳 华

(1.吉林大学 数学学院, 长春 130012; 2.江苏大学 理学院, 江苏 镇江 212013)

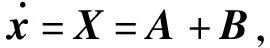
在实际应用中, 许多物理、 化学等领域的微分方程系统都会受随机扰动的影响, 因此考虑具有随机项的微分方程对实际应用有重要意义.文献[9]基于随机向量场的分裂法, 对于一般Stratonovich意义下的具有守恒量的随机微分方程提出了一种新的保守方法, 在求解过程中能保持系统中的守恒量, 且该方法在噪声为可交换时可达到均方1阶收敛; 文献[10]对于Stratonovich意义下的具有守恒量的随机微分方程应用分裂方法求解, 不仅使计算过程中保持守恒量, 而且可以达到与已有的Milstein方法相同的收敛阶, 同时证明了随机微分方程隐格式的收敛性；文献[11]给出了标准布朗运动要满足的3个条件, 同时基于Euler-Maruyama方法和Milstein 方法等给出了数值实例.

近年来, 将分裂方法应用于求解具有一些特殊性质的物理系统受到广泛关注, 如Hong等[12]对于一类具有能量耗散性质的二维Maxwell方程组提出了分裂有限差分时域法, 该方法能保持系统能量耗散的特性, 同时是无条件稳定的; Cai等[13]对于三维时域Maxwell方程组提出了一种指数算子分裂方法, 该方法具有保能量、 高精度、 无条件稳定且节约计算资源等优点; Li等[14]对于非线性Dirac方程提出了4种时间分裂方法, 这些方法都能满足离散能级上的电荷守恒, 且节省了运算时间.本文对一类有守恒量的高维随机Hamilton系统提出一种具有降维和简化运算效果的分裂求解算法.该方法主要利用中点公式构造一种对称的分裂算法, 借助Milstein公式和局部收敛与整体收敛的关系定理得到该方法在均方意义下的整体收敛阶.数值算例结果表明了该方法的有效性.

1 随机Hamilton系统的分裂算法

考虑如下2n维Stratonovich型随机Hamilton系统:

Y: dy(t)=SH(y)dt+TH(y)∘dw(t)，

(1)

其中:y(t)=(y(1)(t),y(2)(t))T∈n×n;S和T是两个斜对称矩阵;w(t)是标准Wiener过程;H(y)是能量函数, 也称为Hamilton函数, 其为满足下述方程的守恒量:

HTSH=0,HTTH=0.

为表示方便, 记

iH∶=y(i)H,iS∶=y(i)S,iT∶=y(i)T,i=1,2.

从而可将方程(1)写成如下形式:

(2)

其中S11,S22,T11和T22均为斜对称矩阵, 且(S12)T=-S21, (T12)T=-T21.

基于对称分裂算法, 可将原系统的向量场Y分解为如下两个子向量场:

(3)

(4)

考虑将方程(1)在时间区间[t0,T]上进行均匀剖分, 步长为h, 剖分节点为tn=t0+nh,n=0,1,…,N, 并记Δw=w(tn+1)-w(tn).在单个时间区间[tn,tn+1]上, 假设y(tn)是方程(1)在tn处的精确解, 用yn表示解y(tn)的数值近似.对式(3)用中点格式离散, 得数值近似格式为

其中：

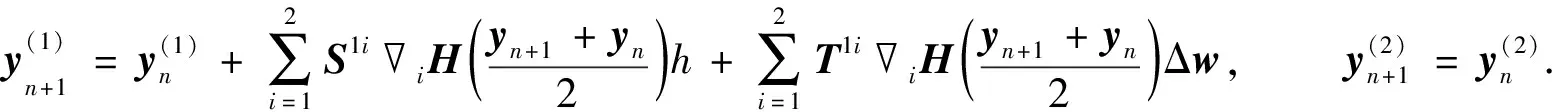
(5)

对式(4)用中点格式离散得数值近似格式为

其中：

(6)

基于分裂法[4]的基本思想, 构造方程(1)在时间区间[tn,tn+1]上的一步近似格式:

(7)

式(7)是一个对称格式.

2 整体收敛性分析

定理1对于2n维Sratonovich型随机Hamilton系统(1), 分裂算法格式(7)在区间[t0,T]上是整体均方一阶收敛的.

证明：在区间[tn,tn+1]上, 假设yn=y(tn).设yM是以yn为初始状态方程(1)的Milstein格式的一步迭代数值近似, 对于k=1,2, 写成如下的分量形式:

(8)

文献[12]给出了Milstein格式的误差阶是均方一阶收敛的.为了证明数值格式(7)的误差阶也是均方一阶的收敛性, 只需证明

(9)

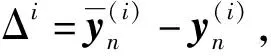
(10)

(11)

进一步做类似地Taylor展开, 可得分裂算法格式(7)的一步近似分量方程为

(12)

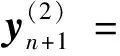
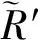
EΔw=0,E(Δw)2=h,E(Δw)3=0,E(Δw)4=3h2,

可得

‖EΔi‖=O(h2), (E‖Δi‖2)1/2=O(h1/2),i=1,2.

(13)

因此, 有如下估计：

(14)

从而由式(8),(12)可以推出

(15)

进而, 式(9)可由式(15)和Minkowski不等式得到.

进一步, 由文献[15]中定理1给出的局部收敛与整体收敛的关系, 可知该分裂算法在区间[t0,T]上的精度p=3/2-1/2=1, 即该方法在均方意义下的整体收敛阶是1阶的.证毕.

3 数值算例

在下面数值算例的计算中, 由于没有精确解, 因此将所取最小步长下求得的数值解作为参考精确解y(tn).定义误差函数

Hamilton函数的误差为

在计算过程中, 固定hn=1.为了得到平均意义下的收敛速率, 对于每个算例, 随机选取 1 000条样本轨道, 然后计算平均值, 从而得到数值解相对于精确解在均方意义下的截断误差.

例1(随机简谐振荡系统) 考虑一个具有一维Wiener过程的Stratonovich型随机简谐振荡系统:

(16)

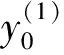
在常系统中它是一个守恒量.易知该系统中S和T是两个斜对称矩阵.应用上述分裂算法数值求解该系统的近似解流.

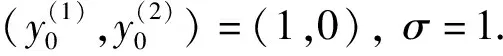
图1 随机简谐振荡系统的截断误差e(tn)和eH(tn)与步长h的关系

例2(随机Kepler系统) 具有一维Wiener过程的随机Kepler系统在Stratonovich意义下的方程为

(17)

该系统是一个四维的随机Hamilton系统, 其中Hamilton函数为

易知该系统中的S和T均为斜对称矩阵.基于分裂算法的主要思想, 可以将该随机Hamilton系统分解为两个二维子系统.

为了验证应用分裂算法数值求解随机Kepler系统的精确性, 观察如图2所示的随机Kepler系统的截断误差e(tn)和eH(tn)与步长h的关系, 其中随机Kepler系统的初值为

由图2(A)可见, 该系统解的误差是一阶收敛的；由图2(B)可见, Hamilton函数的误差也是一阶收敛的.

图2 随机Kepler系统的截断误差e(tn)和eH(tn)与步长h的关系

综上, 通过将本文构造的分裂算法应用于求解随机简谐振荡系统和随机Kepler系统, 验证了理论分析的结果, 表明该分裂算法对于数值求解一类随机微分方程十分有效.