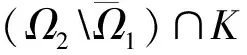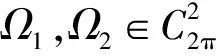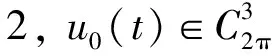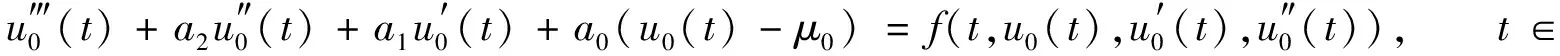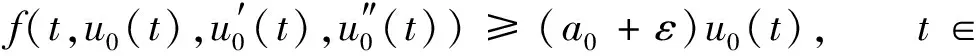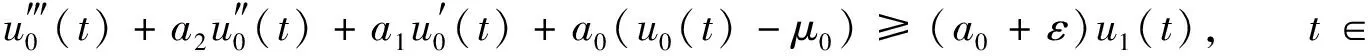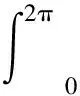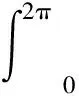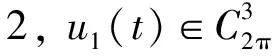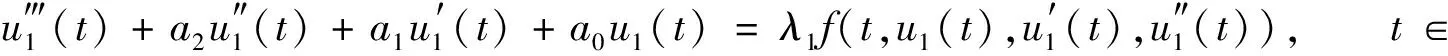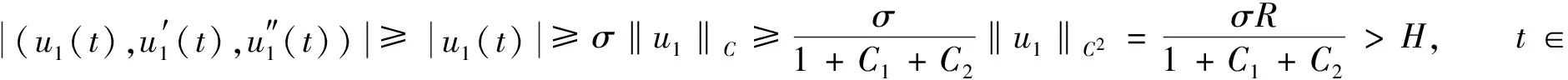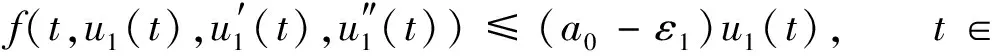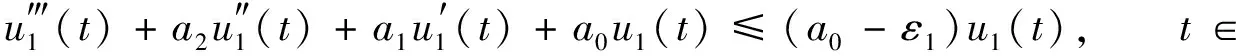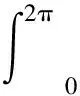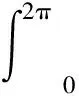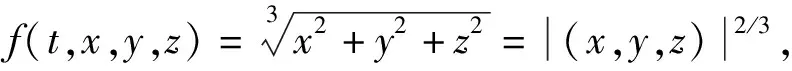一般三阶非线性常微分方程的正周期解
邓正平, 李永祥
(西北师范大学 数学与统计学院, 兰州 730070)
0 引 言
考虑一般三阶常微分方程:
Lu(t)=f(t,u(t),u′(t),u″(t)),t∈
(1)
正2π-周期解的存在性, 其中:Lu(t)=u‴(t)+a2u″(t)+a1u′(t)+a0u(t)是三阶常微分算子,ai∈,i=0,1,2;f:×[0,∞)×2→[0,∞)连续,f(t,x,y,z)关于t以2π为周期.
三阶微分方程在力学、 核物理、 边界层理论等实际问题中应用广泛, 周期现象也普遍存在.目前, 关于三阶非线性周期问题解的存在性研究已有很多结果[1-10]:文献[2]研究了三阶微分方程
u‴(t)+ρ3u(t)=f(t,u(t)), 0≤t≤2π
(2)
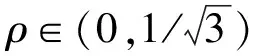
u‴(t)+h(t)u(t)=f(t,u(t)), 0≤t≤2π
(3)
的周期边值问题, 运用锥上的Krasnoselskii不动点定理, 获得了方程(3)正解的存在性结果.其中:h: [0,2π]→[0,∞)连续, 且为非负函数.文献[5]研究了三阶非奇异非线性微分方程
u‴(t)+αu″(t)+βu′(t)=f(t,u(t)),t∈[0,2π],
(4)
其中α,β为正常数, 在满足特定的条件下, 用锥上的Krasnoselskii不动点定理获得了方程(4)正周期解的存在性结果.文献[9]研究了完全三阶微分方程
u‴(t)=f(t,u(t),u′(t),u″(t)),t∈,
(5)
其中f:×[0,∞)×2→连续, 关于t以ω为周期, 用锥上的不动点定理获得了方程(5)正周期解的存在性结果.
受上述研究结果的启发, 本文运用锥上的不动点指数理论, 考虑非线性项f中含有u′,u″的三阶常微分方程(1), 在非线性项f满足特定的增长条件下, 把方程(1)的正2π-周期解问题转化为锥上的不动点问题, 再应用锥上的不动点指数理论获得了方程(1)正2π-周期解的存在性结果.
1 预备知识
记C2π()是以2π为周期的全体连续函数按范数构成的Banach空间.对∀n∈, 记()是以2π为周期的n阶连续可微函数全体按范数构成的Banach空间.记()是C2π()中的非负函数锥.记P(λ)=λ3+a2λ2+a1λ+a0为微分算子L的特征多项式, N(P(λ))表示P(λ)在复平面上的零点集.P(λ)满足假设条件:
(H1)N(P(λ))⊂{z∈||Imz|<1/2}.
引理1[11]假设条件(H1)成立, 且a0>0, 则三阶线性边值问题:
(6)
存在唯一解r(t)∈C3[0,2π], 且对∀t∈[0,2π],r(t)>0.
设h∈C2π(), 考虑线性微分方程
Lu(t)=h(t),t∈
(7)
正2π-周期解的存在性.
引理2假设条件(H1)成立, 且a0>0, 则对∀h∈C2π(), 线性方程(7)存在唯一的2π-周期解
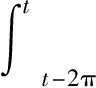
(8)
其中
(9)
为相应的Green函数, 且解算子S:C2π()()为线性全连续算子.
证明:对∀h∈C2π(), 易验证式(8)为线性方程(7)唯一的2π-周期解u∶=Sh.由式(8),(9), 易见解算子S:C2π()()为线性有界算子.由嵌入映射()()的紧性可知,S:C2π())为线性全连续算子.证毕.
根据式(9), 有
(10)
定义正常数σ,C1,C2如下:
(11)
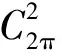
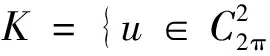
(12)
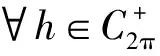
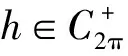
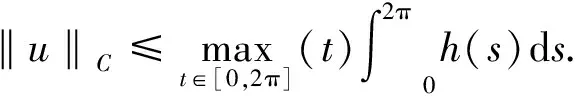
对∀t∈, 由于u(i)(t)=G(i)(t,s)h(s)ds(i=1,2), 从而
故u∈K.证毕.
下面考虑非线性方程(1)的正2π-周期问题.设f:×[0,+∞)×2→[0,∞)连续.对∀u∈K, 令
F(u)(t)∶=f(t,u(t),u′(t),u″(t)),t∈,
(13)
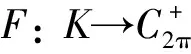
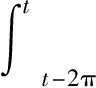
(14)
由算子S的定义, 方程(1)的正2π-周期解等价于A的非平凡不动点.由引理3, 有:
引理4假设条件(H1)成立, 且a0>0, 则由式(14)定义的算子A:K→K为全连续算子.
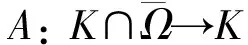
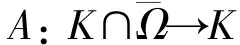
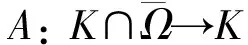
2 主要结果
假设条件:
(H2)存在ε∈(0,a0)且δ>0, 使得当|(x,y,z)|<δ时,f(t,x,y,z)≤(a0-ε)x;
(H3)存在ε>0且H>0, 使得当|(x,y,z)|>H时,f(t,x,y,z)≥(a0+ε)x;
(H4)存在ε>0且δ>0, 使得当|(x,y,z)|<δ时,f(t,x,y,z)≥(a0+ε)x;
(H5)存在ε∈(0,a0)且H>0, 使得当|(x,y,z)|>H时,f(t,x,y,z)≤(a0-ε)x.
定理1假设条件(H1)成立, 且a0>0,f:×[0,+∞)×2→[0,∞)连续,f(t,x,y,z)关于t以2π为周期, 若f满足假设条件(H2),(H3), 则方程(1)至少有一个正2π-周期解.
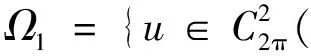
(15)
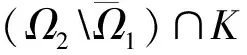
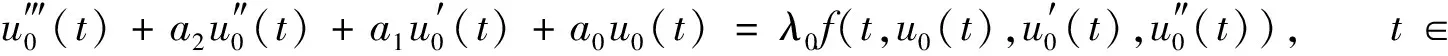
(16)
因为u0∈Ω1∩K, 由K和Ω1的定义, 有
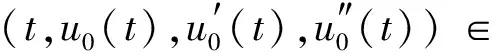
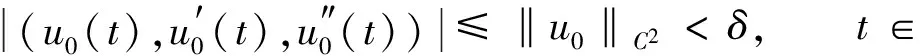
(17)
因此, 由条件(H2), 有
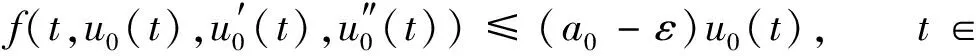
(18)
由式(16)和式(18), 有
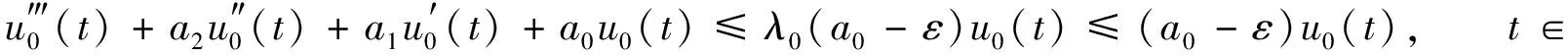
(19)
对式(19)在[0,2π]上积分, 并由u0(t)的2π-周期性, 有
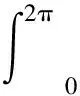
(20)
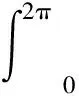
i(A,Ω1∩K,K)=1.
(21)
另一方面, 由条件(H3), 存在ε1>0和H>0, 使得
f(t,x,y,z)≥(a0+ε1)x,t∈, |(x,y,z)|>H.
(22)
令C0=max{|f(t,x,y,z)-(a0+ε1)x|:t∈, |(x,y,z)|≤H}+1, 由式(22), 有
f(t,x,y,z)≥(a0+ε1)x-C0,t∈.
(23)
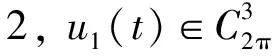
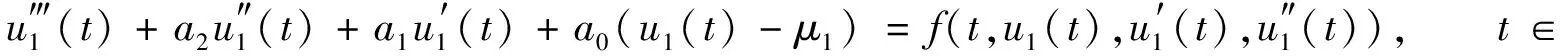
(24)
因为u1∈∂Ω2∩K, 由K的定义, 有
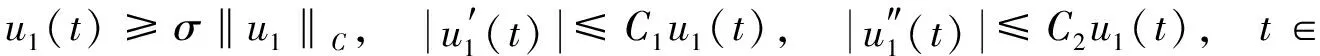
(25)
由式(23), 有
(26)
由式(24),(26), 有
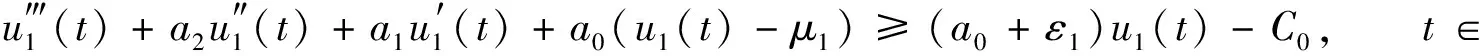
(27)
对式(27)在[0,2π]上积分, 并由u1(t)的2π-周期性, 有
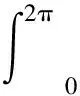
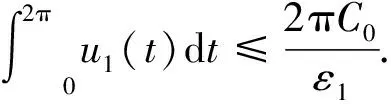
(28)
取R>max{R1,δ}, 则‖u1‖C2≤R1 i(A,Ω2∩K,K)=0. (29) 由不动点指数的区域可加性及式(21),(29), 有 定理2假设条件(H1)成立, 且a0>0,f:×[0,+∞)×2→[0,∞)连续,f(t,x,y,z)关于t以2π为周期, 若f满足假设条件(H4),(H5), 则方程(1)至少有一个正2π-周期解. (30) 因为u0∈Ω1∩K, 由K和Ω1的定义,u0满足式(17), 且由条件(H4), 有 (31) 由式(30),(31), 有 (32) 对式(32)在[0,2π]上积分, 并由u0的2π-周期性, 有 (33) i(A,Ω1∩K,K)=0. (34) 另一方面, 由条件(H5), 存在ε1∈(0,a0)和H>0, 使得 f(t,x,y,z)≤(a0-ε1)x,t∈, |(x,y,z)|>H. (35) (36) 因为u1∈∂Ω2∩K, 由K的定义,u1满足式(25), 则有 所以有 从而由式(35), 有 (37) 由式(36),(37), 有 (38) 对式(38)在[0,2π]上积分, 并由u1(t)的2π-周期性, 有 (39) i(A,Ω2∩K,K)=1. (40) 由不动点指数的区域可加性及式(34),(40), 有 例1考虑如下三阶微分方程: u‴(t)+0.3u″(t)+0.092 5u′(t)+0.007 25u(t)=u2(t)+(u′(t))2+(u″(t))2,t∈. (41) 相应于方程(1), 对应的特征多项式为 P(λ)=λ3+0.3λ2+0.092 5λ+0.007 25=(λ+0.1-0.25i)(λ+0.1+0.25i)(λ+0.1), 满足假设条件(H1), 方程(41)相应于方程(1)的非线性项为f(t,x,y,z)=x2+y2+z2, 易验证满足条件(H2),(H3).由定理1, 三阶微分方程(1)至少有一个正2π-周期解. 例2考虑如下三阶微分方程: (42) 相应于方程(1), 对应的特征多项式为 P(λ)=λ3-0.1λ2+0.052 5λ+0.007 25=(λ-0.1-0.25i)(λ-0.1+0.25i)(λ+0.1),