新型MAX相的相图热力学研究

陈雷雷, 邓子旋, 李勉, 李朋, 常可可,2, 黄峰, 都时禹, 黄庆

新型MAX相的相图热力学研究

陈雷雷1, 邓子旋1, 李勉1, 李朋1, 常可可1,2, 黄峰1, 都时禹1, 黄庆1

(1. 中国科学院 宁波材料技术与工程研究所, 先进能源材料工程实验室(筹), 宁波 315201; 2. 中国科学院大学 材料与光电研究中心, 北京 100049)

本研究通过使用相图计算(Calculation of Phase Diagrams, 简称CALPHAD)耦合第一性原理计算的方法, 以相图作为判断依据, 探究Ti3AuC2、Ti3IrC2、Ti3ZnC2和Ti2ZnC新型MAX相在不同温度下的热力学稳定性。使用相图计算(CALPHAD)方法建立起研究体系的热力学数据库, 耦合第一性原理得到的新型MAX相生成焓数据, 最终得到包含新型MAX相的三元相图。研究结果表明Ti3AuC2、Ti3IrC2、Ti3ZnC2和Ti2ZnC的MAX相具有很好的热力学稳定性, 与实验结果吻合。本研究为确定新型MAX相的热力学稳定性提供了系统的研究方法, 可应用于指导合成更多未知的MAX相材料。

MAX相; CALPHAD; 相图计算; 热力学; 第一性原理计算

MAX相材料是一类具有六方晶体结构的三元层状化合物, 它的分子式是M+1AX(=1, 2或3)。其中, M是过渡族金属元素, A为Ⅲ和Ⅳ主族元素, X是C或者N。MAX相材料的晶胞结构如图1(a)所示, 由MX单元与A层原子交替堆垛而成, 同时拥有MX之间强的共价键和MA之间弱的分子间作用力。正是因为MAX相独特的结构, 导致其兼具金属和陶瓷的一些性能, 例如良好的导电导热性能、低硬度、高弹性模量和剪切模量以及良好的可加工性能、抗氧化和耐腐蚀性能、耐辐照损伤、高屈服强度等[1-3]。

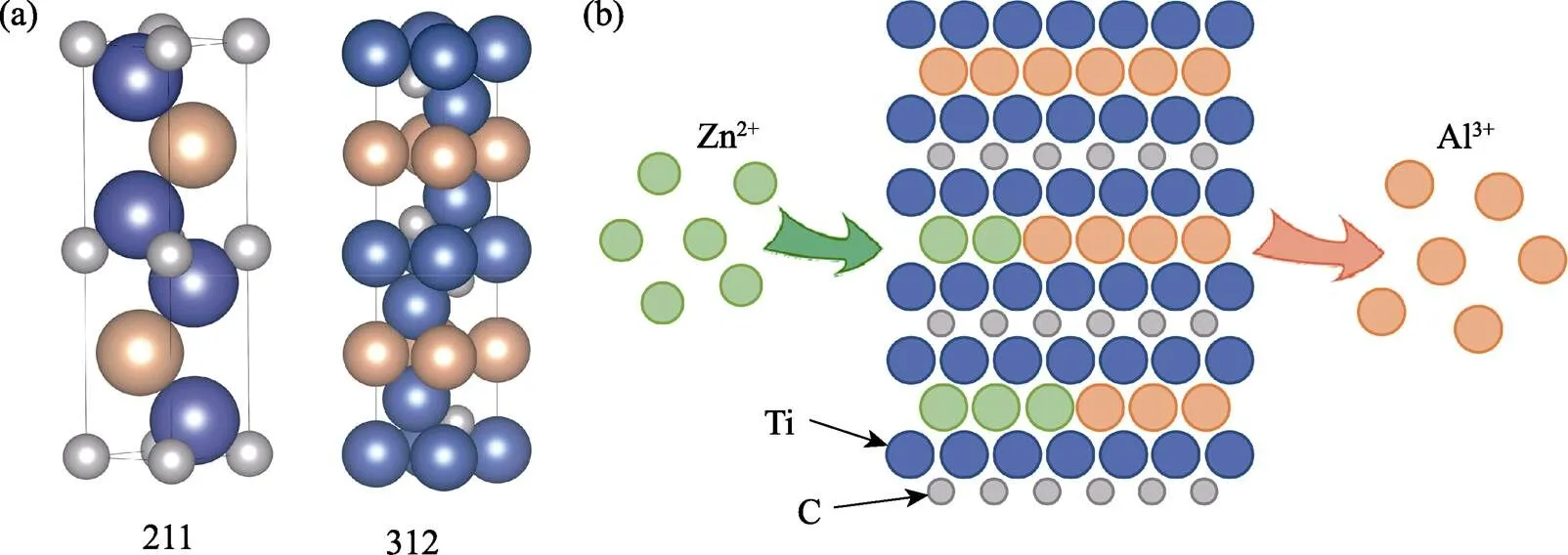
图1 (a) 211型及312型MAX相的晶胞结构; (b)使用熔盐法的A位元素置换策略制备Ti2ZnC的原理示意图[6]

传统MAX相材料中A位元素大多局限在一些Ⅲ和Ⅳ主族元素, 以Al元素为典型代表。近期, 瑞典林雪平大学Eklund团队[4]使用物理气相沉积的方法, 在Ti3SiC2表面沉积了一层Au薄膜, 再经过退火处理, 成功地制备了以Au作为A位元素的新型MAX相Ti3AuC2, 使用相似的方法他们又以Ti3AuC2作为先驱体制备了Ti3IrC2。退火是使体系趋近热力学平衡态的过程, 使用该方法成功制备Ti3AuC2和Ti3IrC2, 表明了他们在热力学上是稳定的。中国科学院宁波材料技术与工程研究所黄庆研究员团队[5-6]使用熔盐法基于A位置换策略以Ti3AlC2、Ti2AlC、Ti2AlN和V2AlC作为先驱体, 与ZnCl2混合, 在550 ℃的环境中成功合成了以Zn作为A位元素的新型MAX相Ti3ZnC2、Ti2ZnC、Ti2ZnN和V2ZnC。熔盐法的实验原理如图1(b)所示。这些新型MAX相的成功制备, 引起了国内外研究者广泛的关注和研究兴趣。传统MAX相中的A位可能被更多的过渡族金属元素替代, 形成新型的MAX相, 而不同A位元素的MAX相性能差异很大, 因此研究新型MAX相对于探究新的材料性能具有非常重要的意义。

仅凭实验合成的方法去探究数量众多的过渡族金属能否占据A位形成稳定的MAX相, 十分耗时耗力。理论计算的方法可以快速地对未知的MAX相体系进行探究, 获得其稳定性, 指导实验合成。如第一性原理计算, 通过比较计算所得的MAX相的生成焓和体系中竞争相的生成焓来确定MAX相的稳定性。然而, 该计算方法获取的是0 K下的结果, 与实际MAX相的合成温度差别很大, 而且受限于计算资源, 只能考虑有限的竞争相, 并不能完全与实验数据符合。

本工作通过研究新型MAX相的相图热力学, 使用耦合第一性原理的相图计算(CALPHAD)的方法, 获取MAX相体系的相图, 以相图作为判断依据, 来探究新型MAX相在不同温度下的热力学稳定性。该方法将相图计算与第一性原理计算耦合到一起, 可以得到新型MAX相在不同温度的稳定性和其与竞争相之间的竞争关系。通过这样的计算方法, 我们获得了Ti–Au–C、Ti–Ir–C和Ti–Zn–C三个体系的相图。从相图中可以得知, 已合成的Ti3AuC2和Ti3IrC2具有很好的热力学稳定性, 而Ti3ZnC2和Ti2ZnC在较低温度下(550 ℃)稳定而在较高温下(1300 ℃)不稳定, 与实验结果相符。

1 研究方法

本研究中使用耦合第一性原理的相图计算(CALPHAD)方法来获取新型MAX相的相图。方法流程见图2, 在第一性原理计算中包含对MAX相结构的弛豫优化以及计算得到新型MAX相的生成焓H, 在相图计算中需要对研究体系进行热力学评估, 建立体系的热力学数据库, 最后将MAX相的生成焓代入到热力学数据库中, 使用热力学软件输出MAX相体系的相图。

1.1 MAX相生成焓:第一性原理计算

MAX相的生成焓是其Gibbs自由能的重要组成部分, 而体系中各个相Gibbs自由能之间的关系最终决定了他们的热力学稳定性。因此MAX相的生成焓作为其相图计算的重要参数, 不可或缺。

本研究通过基于密度泛函理论(DFT)的第一性原理Viennasimulation package (VASP)[7]软件包计算了Ti2AuC、Ti2IrC、Ti2ZnC、Ti3AuC2、Ti3IrC2和Ti3ZnC2六种潜在MAX相的晶格参数和生成焓[8-9]。采用投影缀加波赝势(PAW)[10]来描述电子–离子之间的相互作用, 基于Perdew-Burke-Ernzerhof(PBE)[11]泛函的广义梯度近似法(GGA)来描述电子之间的相互作用, 平面波截断能设为400 eV。计算使用了包含48个原子的原胞, 结构优化均采用完全弛豫优化, 优化精度为原子的能量和力分别收敛于10–4eV和0.1 eV/nm, 采用的K点网格为5×5×3。

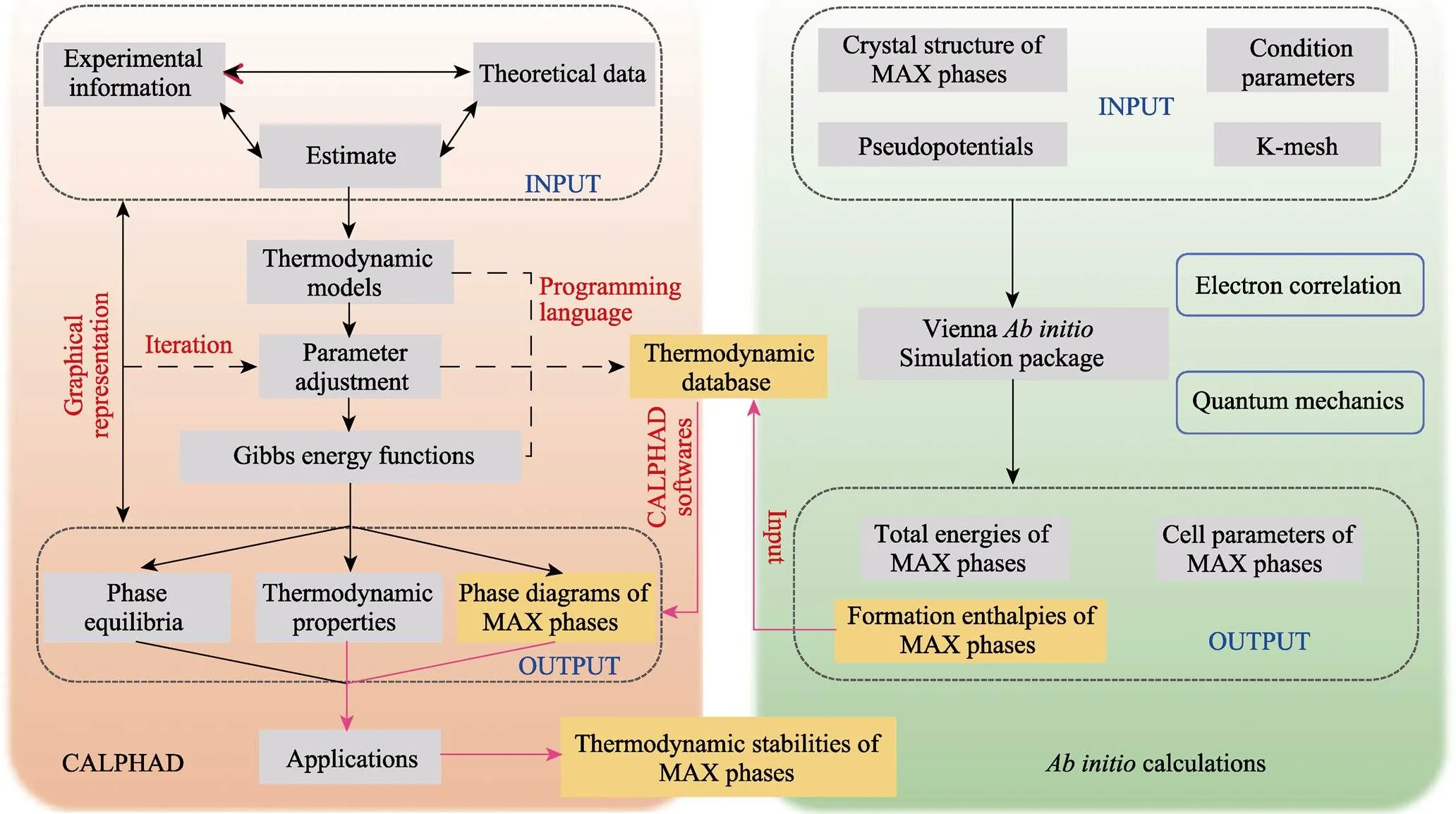
图2 计算(CALPHAD)及第一性原理计算用于获得MAX相相图的方法图解

MAX相在0 K温度下的生成焓用以下公式进行计算:

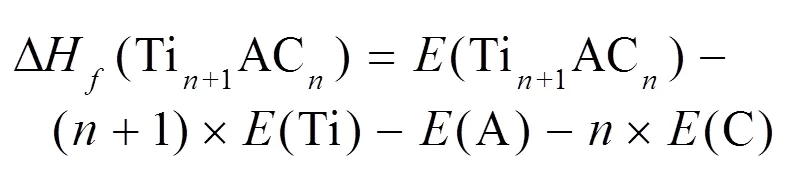
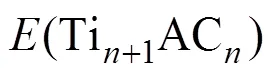
1.2 Gibbs自由能表达式: 相图计算

本文中共包含3个三元体系(Ti–Au–C、Ti–Ir–C、Ti–Zn–C)、7个二元体系(Ti–C、Ti–Au、Ti–Ir、Ti–Zn、Au–C、Ir–C、Zn–C)。针对体系中不同的相采用不同的热力学模型进行描述, 相应地使用不同的Gibbs自由能表达式。

纯元素的热力学数据来源于Dinsdale评估和优化的SGTE (Scientific Group Thermodata Europe)元素数据库[12]。在纯组元中单相的Gibbs自由能可以用以下表达式描述:

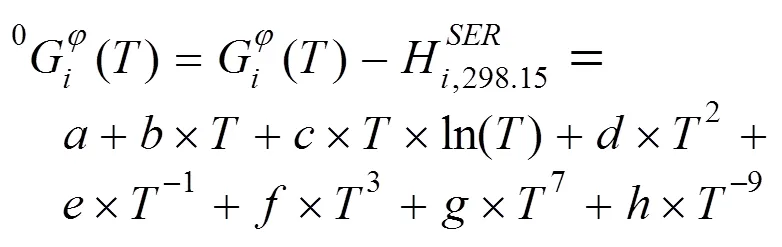
对于体系中的液相及置换固溶体相, 如fcc_A1、bcc_A2、hcp_A3等, 使用置换溶液模型。以Ti–Ir二元系中的Fcc_A1相为例, 其Gibbs自由能表达式可以表述为:

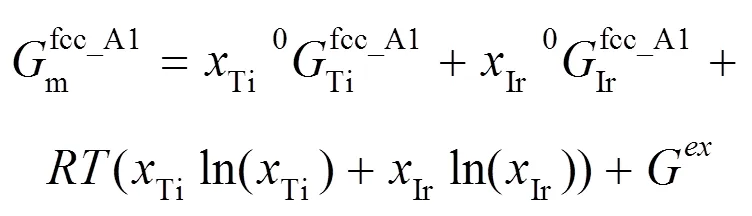
在本研究中包含两种化合物: 化学计量比化合物(又称线性化合物)和有溶解度的化合物。对于化学计量比化合物, 如TiZn、Ti+1AC(A=Au, Ir, Zn)等, 其热容值由Neumann-Kopp规则确定[14], 因此其Gibbs自由能表达式为(以Ti2AuC为例):

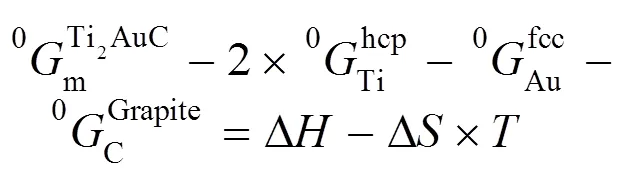
对于有溶解度的化合物, 如Ti3Ir、TiIr3、TiAu等, 使用亚点阵模型描述[15]。以TiAu相为例, 其热力学模型可以表示为(Ti, Va)1(Ti, Au)1。其Gibbs自由能表达式为:

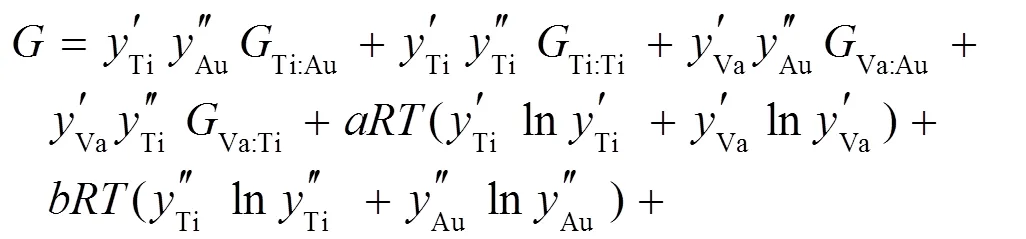
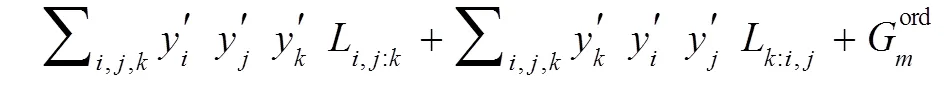
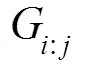
本研究中Ti–C、Ti–Au、Ti–Ir、Ti–Zn、Zn–C二元体系数据库分别引用自Gorbachev[16]、Luo[17]、Wang[18]、Deng[19]和Hämäläinen[20]等的工作。Au–C和Ir–C二元体系由于缺少实验数据因此文献中并没有热力学数据报道, 且Au–C和Ir–C体系中都有没有中间化合物。对于Au–C体系, 本文调节了其液相参数使得其共晶反应温度(1050.7 ℃)与Okamoto等[21]评估的结果(1050 ℃)相近; 对于Ir–C体系, 由于不加入任何热力学参数时其共晶反应温度(2319 ℃)已经与实验结果[22](2296 ℃)接近, 因此本文中没有引入更多的热力学数据。由于Au–C和Ir–C体系中均不包含中间相, 因此其对MAX相的稳定性结果的影响可以忽略。

2 结果与讨论

2.1 MAX相的生成焓

本文中通过第一性原理优化了Ti2AuC、Ti2IrC、Ti2ZnC、Ti3AuC2、Ti3IrC2和Ti3ZnC2六种MAX相的晶体结构, 并计算得到了其生成焓。表1为计算得到的MAX相的晶格参数和生成焓。与实验数据[4-6,23]对比可知, 计算得到的Ti3AuC2和Ti3ZnC2的晶格参数比较准确。

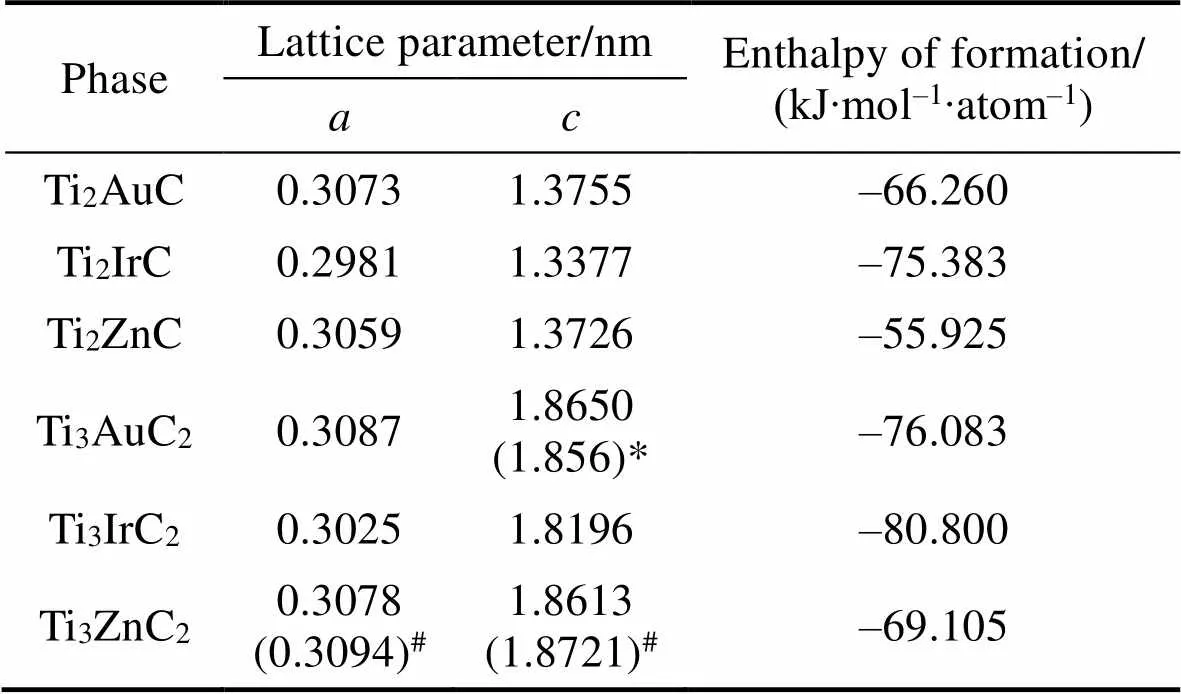
表1 MAX相的晶胞参数和生成焓

*Lattice parameters of Ti3AuC2synthesized by Flashandi,[4, 23];#Lattice parameters of Ti3ZnC2synthesized by Li,[5-6]

2.2 Ti–Au–C体系的相图

图3为计算得到的Ti–Au–C体系的在不同温度下(550和1300 ℃)的等温截面图。从相图中可以得知, Ti3AuC2和Ti2AuC相在550和1300 ℃都可以稳定存在。在550 ℃时, Ti3AuC2和Ti2AuC相与TiC、TiAu及TiAu2相形成了一些三相区, 因此在550 ℃时, Au-MAX相的主要竞争相是TiC、TiAu和TiAu2相。在1300 ℃的相图中, 富Au端已经出现了Liquid的单相区, 并且Liquid、TiC和Ti3AuC2相形成了一个三相区, 表明Ti3AuC2有很高的熔点。在1300 ℃时, Au-MAX相的竞争相相比较550 ℃时增加了Liquid相。Fashandi等[4]使用物理气相沉积的方式, 在Ti3SiC2上沉积一层很薄的Au, 然后将样品在670 ℃退火, 成功制备了Ti3AuC2。而在本文计算的结果中, Ti3AuC2相同时出现在了550和1300 ℃的相图上, 表明其在计算的温度范围内(550~1300 ℃)都是热力学稳定的。

2.3 Ti–Ir–C体系的相图

Ti–Ir–C体系的相图计算结果如图4所示。在550 ℃的等温截面相图中只存在Ti3IrC2相一个MAX相, 而在1300 ℃的等温截面相图中同时出现了Ti3IrC2和Ti2IrC相。由此可知, Ti2IrC相只能在较高的温度下稳定, 在低温下会分解成其他相, 而Ti3IrC2相有很好的热力学稳定性。Ti2IrC相的高温稳定而低温不稳定现象, 说明该MAX相可以在高温下被合成, 但是由于其不具备中低温的热力学稳定性, 在中低温服役过程中可能会分解。在550 ℃温度下Ir-MAX相的竞争相与1300 ℃时完全相同, 都是TiC、TiIr、TiIr和TiIr3相。Fashandi等[4]使用Ti3AuC2作为前驱体, 成功在600 ℃下制备出了Ti3IrC2, 与本研究中相图计算的结果相符。

2.4 Ti–Zn–C体系的相图

在Ti–Zn–C体系中, Ti2ZnC和Ti3ZnC2相可以同时出现在550 ℃的等温截面相图中, 如图5所示。由于Zn的熔点只有419.53 ℃, 因此在相图的富Zn端已经出现了稳定的Liquid相, 而Ti–Zn二元相图中众多的化合物也让Zn-MAX相的竞争环境变得十分复杂。TiC、Ti2Zn、TiZn、TiZn2、TiZn3、Ti3Zn22和Liquid相都是Zn-MAX的竞争相。在温度升高到1300 ℃时, 由于富Zn端出现了稳定的Gas相, 导致体系中的三元化合物都不再稳定, 因此Zn-MAX相没有出现在1300 ℃的相图中。近期Li等[5-6]使用基于A位替代策略的熔盐法, 以Ti3AlC2和Ti2AlC为前驱体在550 ℃下成功合成了Ti2ZnC和Ti3ZnC2相, 这与本文中的计算结果高度符合。同时, 实验结果也表明Ti2ZnC和Ti3ZnC2相在高温下会分解。

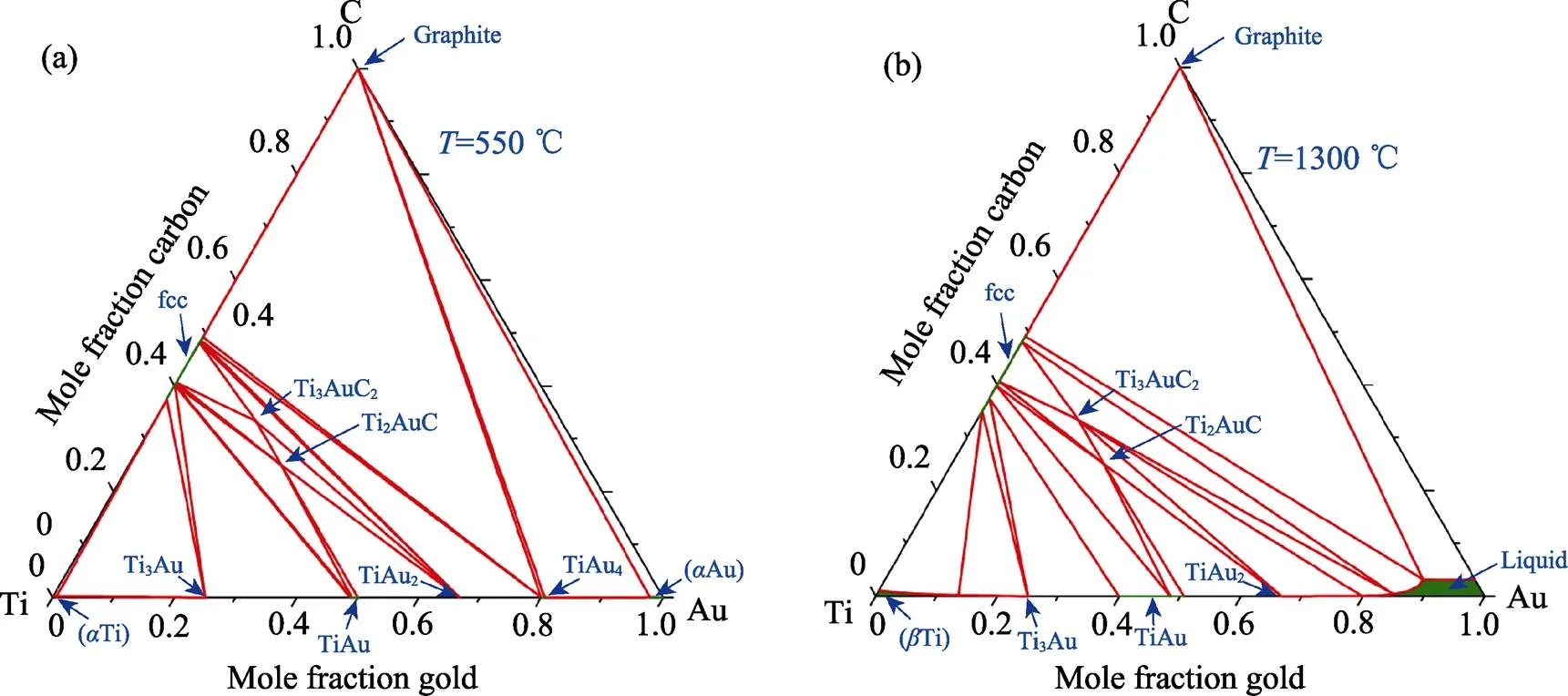
图3 计算的Ti–Au–C体系相图在不同温度下的等温截面图

(a) 550 ℃; (b) 1300 ℃

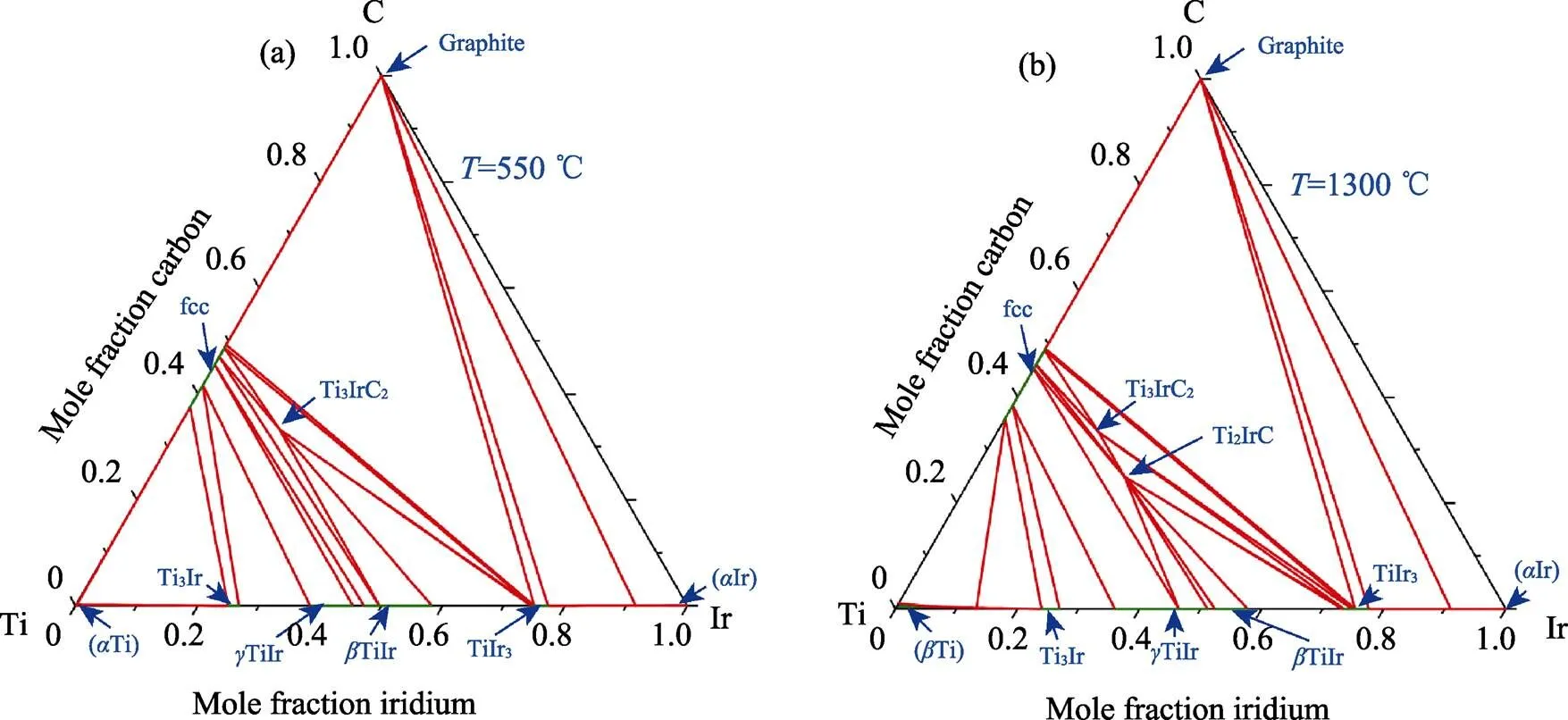
图4 计算的Ti–Ir–C体系相图在不同温度下的等温截面图

(a) 550 ℃; (b) 1300 ℃

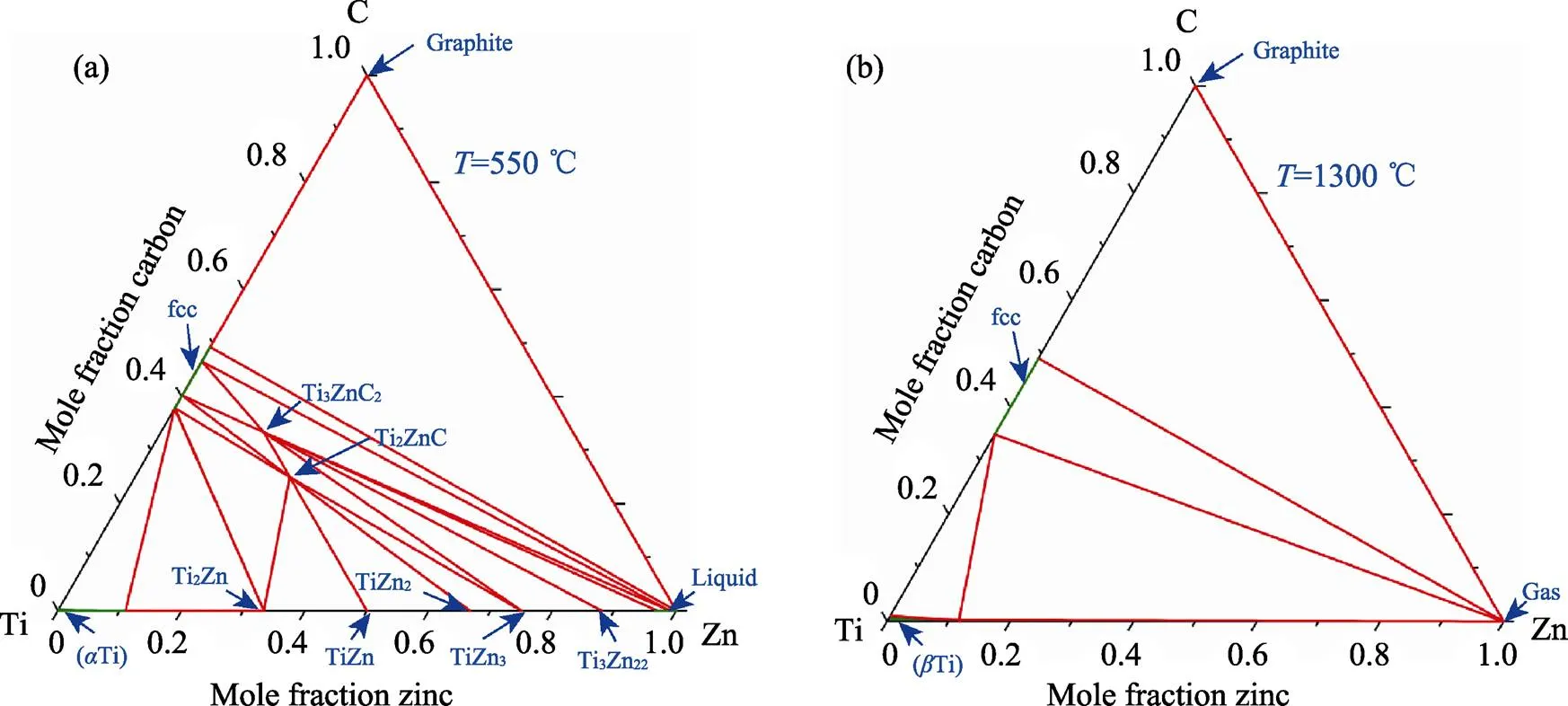
图5 Ti–Zn–C体系相图在不同温度下的等温截面图

(a) 550 ℃; (b) 1300 ℃

3 结论

本工作提出了新型MAX相的相图研究方法, 通过使用耦合第一性原理的相图计算(CALPHAD)方法, 成功得到了Ti–Au–C、Ti–Ir–C和Ti–Zn–C体系的三元等温截面相图。同时, 以相图作为新型MAX相稳定性的判据, 得到了Ti2AuC、Ti2IrC、Ti2ZnC、Ti3AuC2、Ti3IrC2和Ti3ZnC2六种MAX相在550和1300 ℃的热力学稳定性。本文中研究的温度(550和1300 ℃)分别对应新型MAX相制备方法中的熔盐法和等热静压法的典型温度, 因此计算结果可以用于指导实验合成新型MAX相。此外, 实验合成路径中先驱体的选择也会影响新型MAX相的合成结果。使用相图热力学研究思路, 针对新型MAX相先驱体的选择需要进一步探究。

本研究中的计算方法在材料的具体合成温度来计算其稳定性, 并且考虑了体系中所有的竞争相, 这使得计算的结果更加贴近实验条件。对于文献中已经合成的Ti3AuC2、Ti3IrC2、Ti3ZnC2和Ti2ZnC四种MAX相, 本文中的计算结果与实验结果完全吻合。本研究可以扩展到其他的MAX相体系中, 形成一套计算潜在MAX相稳定性的有效方法, 对于实验合成新型MAX相有重要的指导意义。

[1] CHING W Y, MO Y, ARYAL S,. Intrinsic mechanical properties of 20 MAX-phase compounds., 2013, 96(7): 2292–2297.

[2] SUN Z M. Progress in research and development on MAX phases: a family of layered ternary compounds., 2011, 56(3): 143–166.

[3] BARSOUM M W. The MAXphases: a new class of solids., 2000, 28: 201–281.

[4] FASHANDI H, DAHLQVIST M, LU J,. Synthesis of Ti3AuC2, Ti3Au2C2and Ti3IrC2by noble metal substitution reaction in Ti3SiC2for high-temperature-stable Ohmic contacts to SiC., 2017, 16: 814.

[5] LI M, LI Y, LUO K,. Synthesis of novel MAX phase Ti3ZnC2A-site-element-substitution approach., 2019, 34(1): 60–64.

[6] LI M, LU J, LUO K,. Element replacement approach by reaction with Lewis acidic molten salts to synthesize nanolaminated MAX phases and MXenes., 2019, 141(11): 4730–4737.

[7] KRESSE G, FURTHMÜLLER J. Efficient iterative schemes fortotal-energy calculations using a plane-wave basis set., 1996, 54(16): 11169–11186.

[8] LIU S, CHANG K, MRÁZ S,. Modeling of metastable phase formation for sputtered Ti1–xAlN thin films., 2019, 165: 615–625.

[9] CHANG K, TO BABEN M, MUSIC D,. Estimation of the activation energy for surface diffusion during metastable phase formation., 2015, 98: 135–140.

[10] JOUBERT D, KRESSE G. From ultrasoft pseudopotentials to the projector augmented-wave method., 1999, 59(3): 1758–1775.

[11] BURKE K, ERNZERHOF M, PERDEW J P. Generalized gradient approximation made simple., 1996, 77(18): 3865–3868.

[12] DINSDALE A T. SGTE data for pure elements., 1991, 15(4): 317–425.

[13] REDLICH O, KISTER A T. Thermodynamics of nonelectrolyte solutions-xyt relations in a binary system., 1948, 40(2): 341–345.

[14] CHANG K, DU Y, SUN W,. Thermodynamic assessment of the V–Zn system supported by key experiments and first-principles calculations., 2010, 34(1): 75–80.

[15] CHEN L, ZHANG Z, HUANG Y,. Thermodynamic description of the Fe–Cu–C system., 2019, 64: 225–235.

[16] GORBACHEV I I, POPOV V V. Analysis of the solubility of carbides, nitrides, and carbonitrides in steels using methods of computer thermodynamics: III. Solubility of carbides, nitrides, and carbonitrides in the Fe–Ti–C, Fe–Ti–N, and Fe–Ti–C–N systems., 2009, 108(5): 484–495.

[17] LUO W, JIN Z, LIU H,. Thermodynamic assessment of the Au–Ti system., 2001, 25(1): 19–26.

[18] WANG C, GUO Y, YONG L,. Thermodynamic assessment of the Ti–Ir system., 2014, 35(3): 269–275.

[19] DENG Z, ZHAO D, HUANG Y,. Unpublished research. 2018.

[20] HÄMÄLÄINEN M, ISOMÄKI I. Thermodynamic evaluation of the C–Co–Zn system., 2005, 392(1): 220–224.

[21] OKAMOTO H, MASSALSKI T B. The Au–C (gold-carbon) system., 1984, 5(4): 378–379.

[22] NADLER M R, KEMPTER C P. Some solidus temperatures in several metal-carbon systems., 1960, 64(10): 1468–1471.

[23] FASHANDI H, LAI C C, DAHLQVIST M,. Ti2Au2C and Ti3Au2C2formed by solid state reaction of gold with Ti2AlC and Ti3AlC2., 2017, 53(69): 9554–9557.

Phase Diagrams of Novel MAX Phases

CHEN Lei-Lei1, DENG Zi-Xuan1, LI Mian1, LI Peng1, CHANG Ke-Ke1,2, HUANG Feng1, DU Shi-Yu1, HUANG Qing1

(1. Engineering Laboratory of Advanced Energy Materials, Ningbo Institute of Industrial Technology, Chinese Academy of Sciences, Ningbo 315201, China; 2. Center of Materials Science and Optoelectronics Engineering, University of Chinese Academy of Sciences, Beijing 100049, China)

Phase diagrams are used as an indicator to estimate the thermodynamic stabilities of the novel MAX phases (Ti3AuC2, Ti3IrC2, Ti3ZnC2, Ti2ZnC). The phase diagrams of the Ti–Au–C, Ti–Ir–C, and Ti–Zn–C systems were obtained using the CALPHAD (Calculation of Phase Diagrams) approach coupled withcalculations. The calculated results confirmed thermodynamic stabilities of the synthesized Ti3AuC2, Ti3IrC2, Ti3ZnC2, and Ti2ZnC MAX phases, which is in great agreement with the experiment information. The present work shows a systematic method to calculate the thermodynamic stability of the novel MAX phases, which can be used as guidance to synthesize more undiscovered MAX phases.

MAX phase; CALPHAD; calculation of phase diagrams; thermodynamics;calculations

TQ174

A

1000-324X(2020)01-0035-06

10.15541/jim20190184

2019-04-29;

2019-07-25

国家自然科学基金(51701232); 中国科学院率先行动“百人计划”(2017-118)

National Natural Science Foundation of China (51701232); CAS Pioneer Hundred Talents Program (2017-118)

陈雷雷(1993–), 男, 硕士研究生. E-mail: chenleilei@nimte.ac.cn

CHEN Lei-Lei(1993–), male, Master candidate. E-mail: chenleilei@nimte.ac.cn

常可可, 研究员. E-mail: changkeke@nimte.ac.cn

CHANG Ke-Ke, professor. E-mail: changkeke@nimte.ac.cn