基于模糊输出反馈的永磁涡流耦合器调速系统研究

高庆忠，邱健鹏，高浩然，韩钧如，杨 柏，杨 亮

（1.沈阳工程学院a.自动化学院；b.研究生部，辽宁 沈阳 110136；2.国网营口供电公司，辽宁 营口 115000；3.国网辽宁省电力有限公司检修分公司，辽宁 沈阳 110000；4.国网张掖供电公司，甘肃 张掖 734000）

永磁涡流耦合器属于新兴设备，其优点在于具有良好的节能效果和很强的过载保护能力，还有成本低廉、可靠性高的特点，在电力、船舶、石油等领域广泛应用。永磁涡流耦合器的主要作用是通过改变输出转矩进行速度调节，调节方法为改变导体转子与永磁体转子之间的气隙宽度或耦合面积。永磁涡流耦合器的调速控制问题归根结底是控制气隙宽度（或耦合面积）问题。因此，需要建立一个控制系统实现对永磁涡流耦合器的气隙宽度（或耦合面积）的控制。由于永磁电机与永磁涡流耦合器的结构类似但是不尽相同，故永磁电机的控制方法不能直接应用于永磁涡流耦合器的控制，所以研究用永磁涡流耦合器的结构原理制定相应的控制策略对于永磁调速器领域的研究有着一定的学术意义和创新意义。

周丽娜［1］提出了一种模糊神经网络控制器，该控制器同时具有模糊控制和神经网络的优点，应用在电机调速系统中，通过仿真研究证明了效果较好。李鹏飞等人［2］以相邻偏差控制为控制策略，对多个直流伺服电机的同步控制进行了研究，输入端为相邻两台电机的转速偏差和偏差变化率，利用模糊自适应PID 补偿器补偿电机的反馈误差。张碧陶等人［3］根据传统整数阶滑膜控制的抖震问题，将分数阶理论、模糊逻辑推理、滑膜控制技术的优点相结合，提出改良后的将整数阶切换面推广到分数阶的模糊分数阶滑膜控制策略，设计出的全控制域滑膜面能够保证系统较强的鲁棒性。邵子楠［4］提出了两种位置控制回路自抗扰控制器的设计方法；首先，研究了自抗扰控制器的控制方法和应用范围，并将其应用于盘式永磁调速系统的调速回路中，实现对双直流转矩电机的控制；最后，采用Si‐milink平台对控制效果进行仿真分析。关晓娜［5］在自抗扰控制算法参数众多、优化速度慢的基础上，提出QPSO-ADRC 算法的永磁调速器控制系统研究，在优化过程中使用量子粒子群算法，对永磁调速器的调速系统相关参数进行优化，并使用MAT‐LAB进行仿真验证，最终得出量子粒子群算法优化的控制器具有优化参数快、优化过程简单等优点。荆建立等人［6］提出了一种新型的无刷直流电机模糊参数自适应PID 控制，不仅对无刷直流电机的数学模型、运行特性进行分析，还细致地对模糊参数适应PID 控制器的工作原理进行了阐述，根据以上基础设计了无刷直流电机的模糊参数自适应PID控制器，取得了理想的结果。

目前，非线性控制领域学者对于非线性系统的观测器型输出反馈控制问题进行了深入研究并取得了若干重要成果［7］：基于T-S 模糊模型的滤波器设计［8-9］、不同的模糊观测器设计［10-11］、T-S 模糊系统设计［12］、T-S 模糊系统的动态输出反馈控制［13］、基于模糊观测器的输出反馈控制设计［14-15］、通过双线性矩阵不等式来计算基于观测器的控制器［16］等等。值得指出的是，以上控制方案针对混合式永磁涡流耦合器转速控制效果并不理想。为了进一步解决这个问题，基于拓维思想，本文设计了一种非线性系统的观测器型输出反馈控制方案，并将其用于试验平台的控制，取得了理想的设计效果。

1 永磁涡流耦合系统调速原理

永磁涡流耦合系统调速原理如图1 所示。一般来说，永磁涡流耦合器的导体转子与电机输出轴连接，导体转子只与电机一起作旋转运动，导体转子在水平方向上相对于永磁涡流耦合器外壳是静止的。因此，永磁涡流耦合器的导体转子也可称为定子部分［17-18］。永磁涡流耦合器通过调节永磁体转子水平位置运动，因此永磁体转子也可称为转子部分。永磁涡流耦合器的调速部件包括推动电机、丝杆、永磁涡流耦合器永磁体转子。丝杆的一端与推动电机输出轴连接，另一端与永磁涡流耦合器的永磁体转子连接。丝杆可以将推动电机的旋转运动转化为永磁体转子的水平直线运动。调节气隙宽度或耦合面积，最终实现调速。

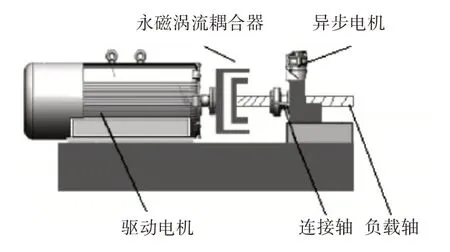
图1 永磁涡流耦合系统调速原理

2 控制策略

2.1 推动电机模糊建模

永磁涡流耦合器调速系统的模糊控制模型，即推动电机模型采用文献［19］中建立的伺服电动机动态模型，其模型如式（1）所示：

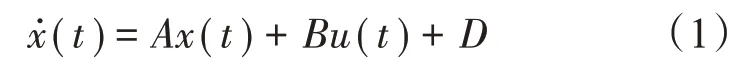
其中，状态向量x(t)=[ωψd id iq]T；控制向量u(t)=[ud uq]T；系数矩阵A、B和D分别表示系统矩阵、输入矩阵以及静态矩阵，其表示方式为

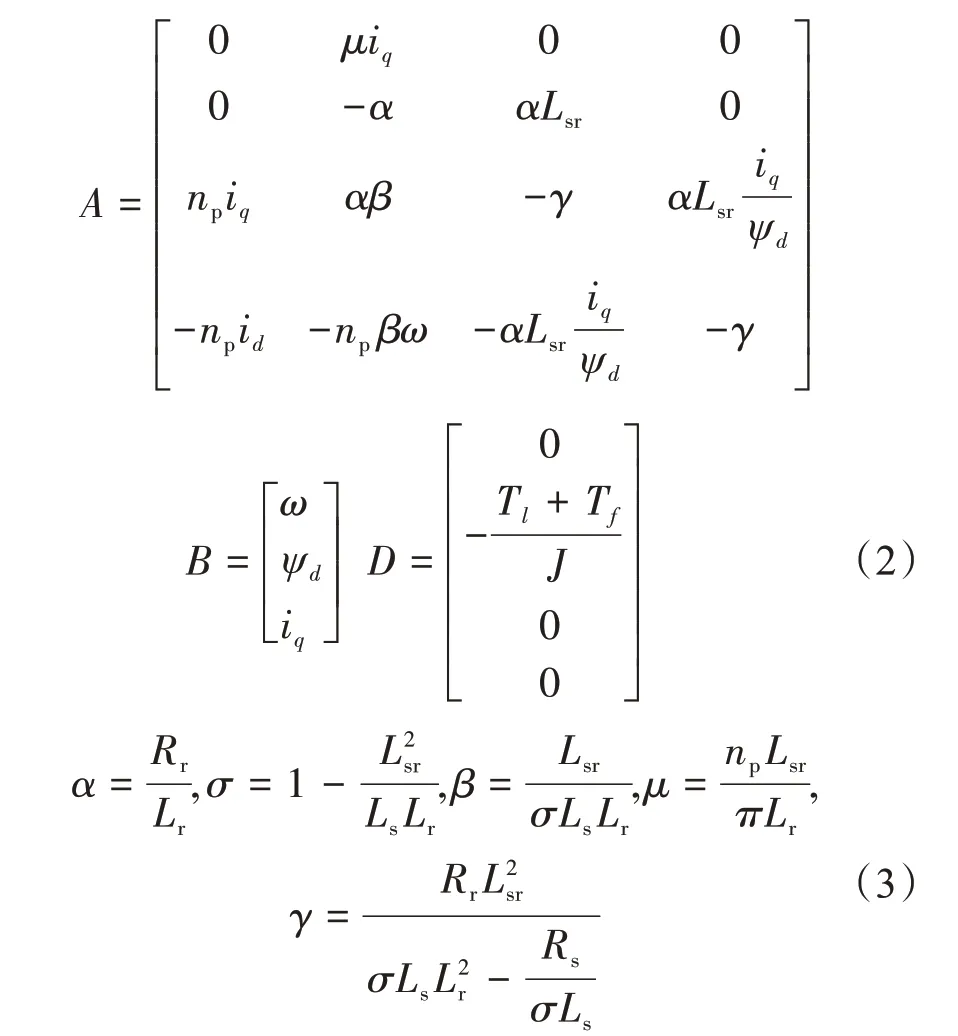
式中，ω为伺服电机机械角速度；id为d轴定子电流；iq为q轴定子电流；Ls为定子自感；Lr为转子自感；Lsr为定子与转子的互感；σ为漏感系数；Rs为定子电阻；Rr为转子电阻；np是转子磁极对数；J为转动惯量；Tl为负载转矩；Tf为摩擦转矩。

推进电机的模糊模型为

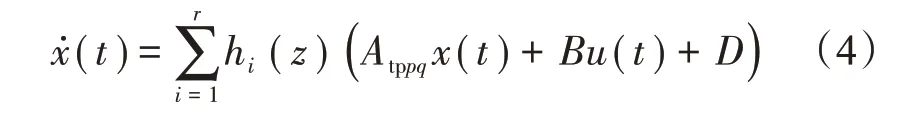
其模糊论域如下：

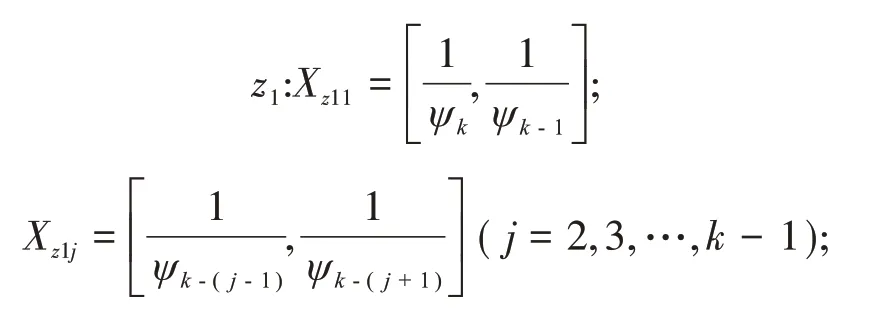
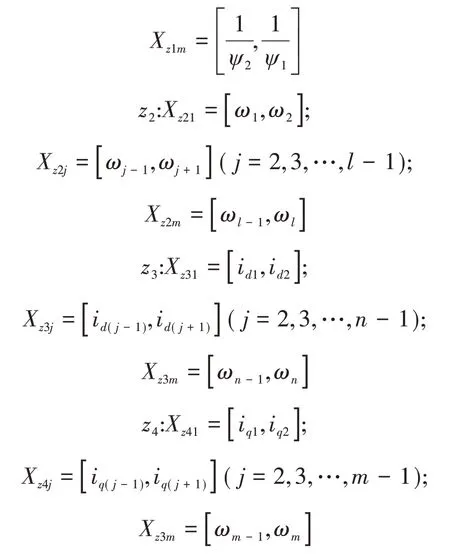
2.2 模糊输出反馈控制器模型

模糊输出反馈控制器的结构如下：

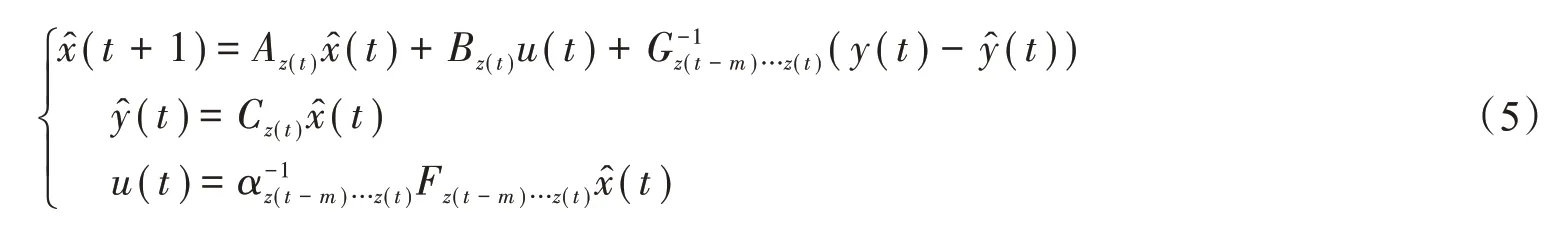
式中，y(t)为由位置传感器光电编码器提供的可测系统输出信号。

则

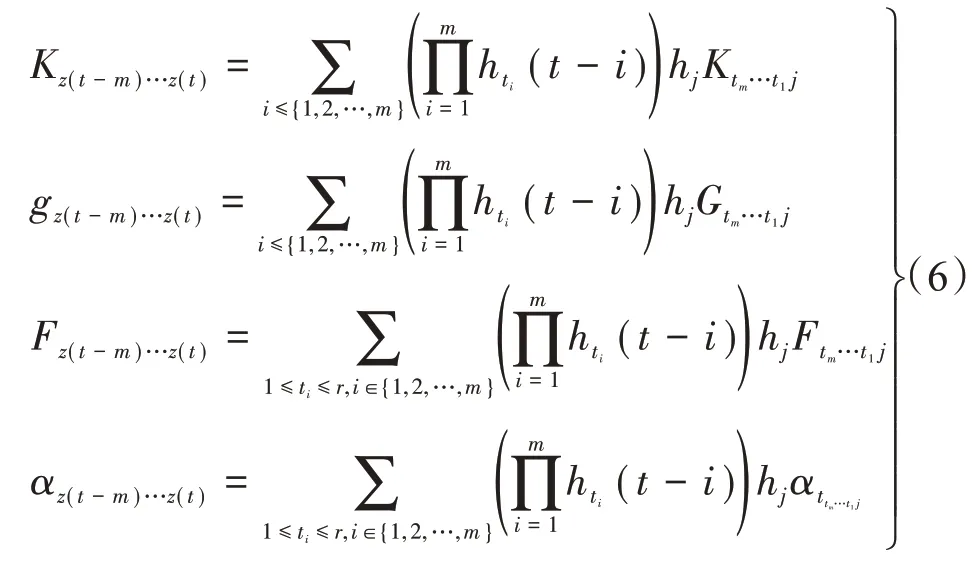
式中，Ktm…t1j、Gtm…tij、Ftm…t1j和αtm…t1j为待求的输出反馈控制增益矩阵。

结合式（5）和式（6），得到闭环控制系统公式为

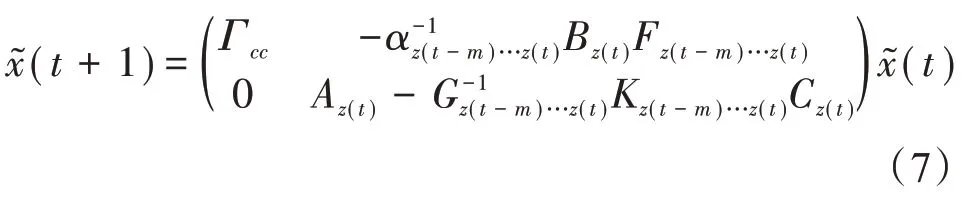
由现代控制理论可知，如果闭环控制系统（8）的所有线性矩阵不等式同时成立，那么（7）就是全局渐近稳定的。

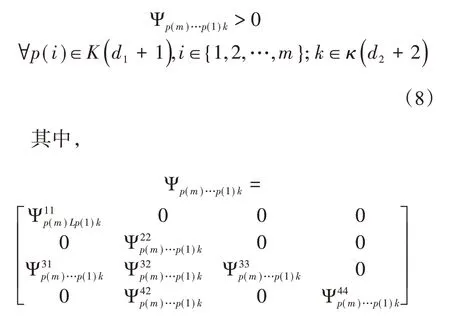
3 仿真研究

为了验证本文控制方法在永磁涡流耦合调速系统的实用性与先进性，分别对应用本文的模糊控制器和传统PID 控制器［17］的永磁涡流耦合调速系统进行干扰特性和转差特性的仿真研究。

3.1 干扰特性仿真

前文在详细地介绍了永磁调速器控制系统函数模型表达式的同时，也确定了系统的数学模型。然而在实际运行过程中存在扰动，为了增加与实际情况的相似度，在系统中加入扰动并对其进行仿真，仿真结果如图2所示。

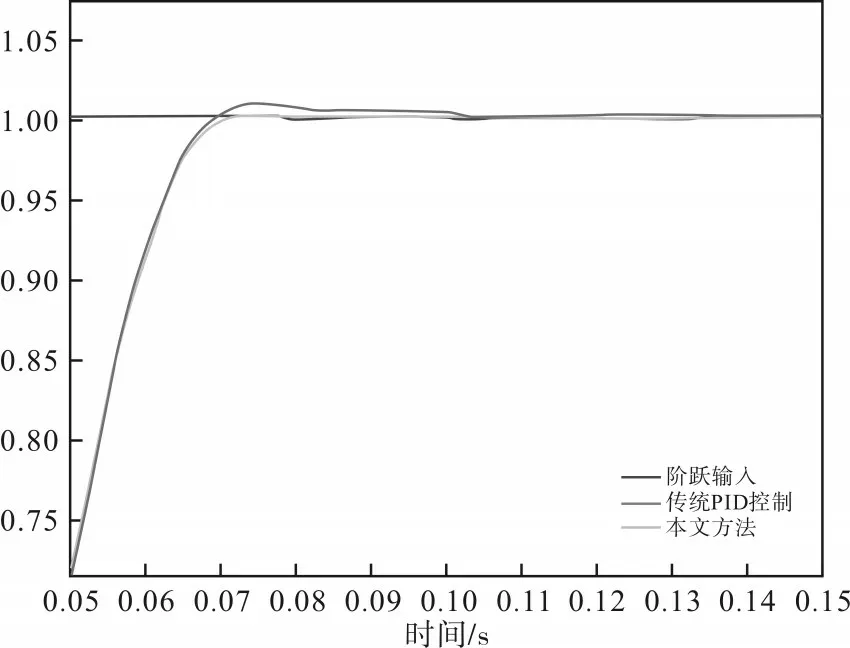
图2 阶跃响应曲线

由图2 可以看出，在传统PID 算法控制系统和本文算法控制系统中，输入阶跃函数和输入相同的扰动，当系统使用本文算法时，可以维持良好的动态性能和稳态性能，同时可以更快地响应。图2 中响应时间约为0.057 s，并且基本无超调。

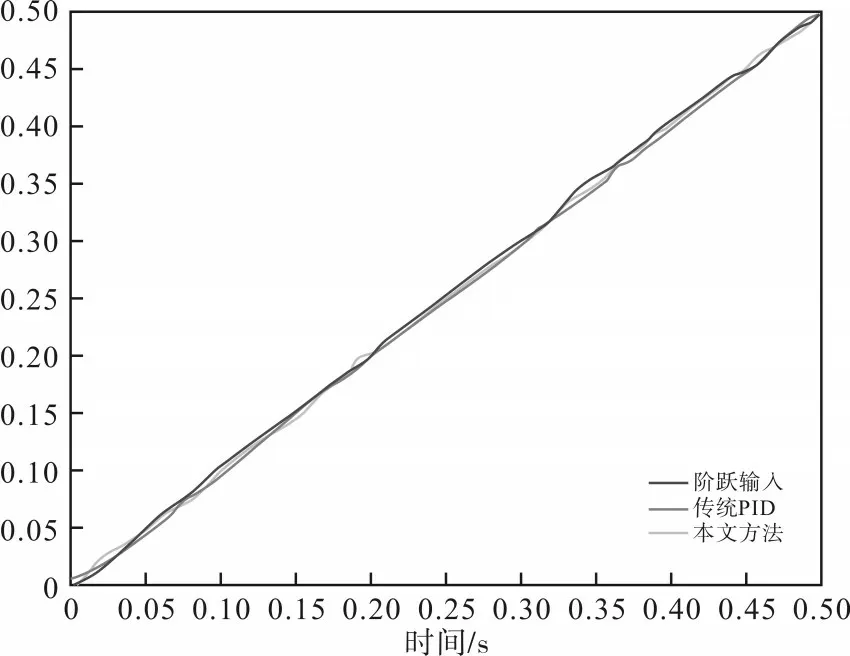
图3 斜坡相应曲线

图3 对比了在相同控制器参数条件下，使用传统PID 算法与本文算法的ADRC 控制系统的单位斜坡响应曲线，两者几乎完全一致。图4 为相应的误差曲线，当使用本文方法时，精确度对比传统方式有了很大地提高，系统性能也更加稳定、可靠。

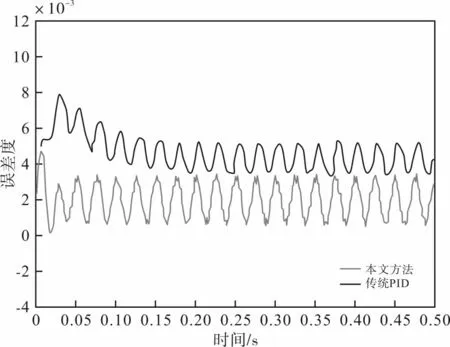
图4 斜坡响应误差曲线

3.2 转差特性仿真

对两种闭环控制系统进行计算机仿真得到仿真图形，如图5、图6 所示，其中图5 为采用传统PID控制器的仿真图，而图6 为采用本文设计的可任意拓维基于观测器型的控制器。

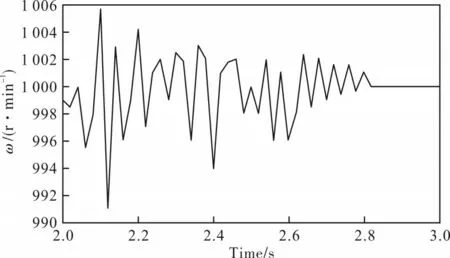
图5 传统PID控制器

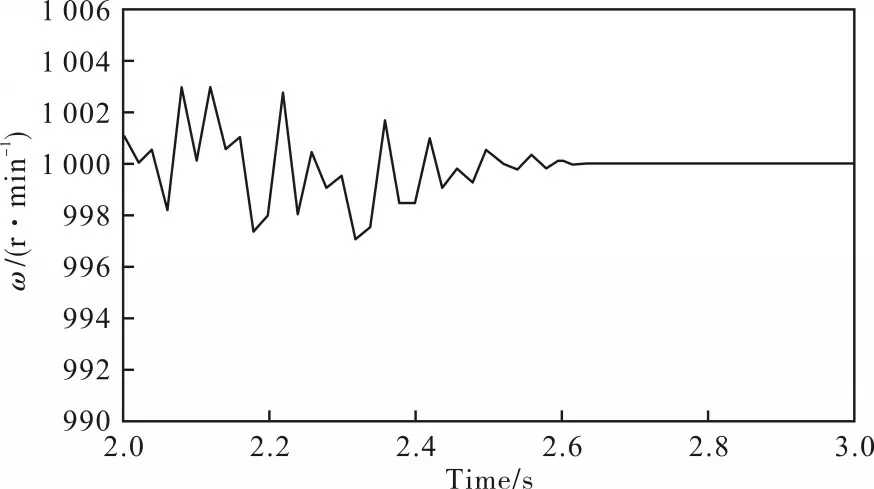
图6 基于观测器型的控制器

从图5 可以看出，试验平台采用传统PID 控制器的情况下，混合式永磁涡流耦合器从启动至达到设定转差的过程中，仿真曲线经历了一个衰减震荡的过程且震荡幅度较大，这说明转差调节范围较大、调节时间较长、控制效果差。从图6 可以明显看出，与图5采用传统PID控制器的试验平台相比，采用本文设计的可以任意拓维的基于观测器型的模糊控制器具有以下优点：

1）调节时间缩短。系统采用传统的PID 控制器达到稳态的时间为2.82 s，采用本文设计的控制器达到稳态的时间为2.6 s。

2）超调量小。采用传统PID 控制的超调量为0.6%，采用本文设计的控制器超调量为0.3%。

4 结论

本文提出了一种基于模糊输出反馈混合式永磁涡流耦合器调速系统的控制策略，本文方法显著提高了混合式永磁涡流耦合器调速控制系统的鲁棒性与控制精度。相比于传统的PID 控制方法，本文方法可以维持良好的动态性能和稳态性能，同时可以更快地响应；精确度比传统方式有了很大地提高，系统性能也更加稳定、可靠；能够快速地达到稳态，缩短调节时间，且降低了超调量。本文所提出的控制设计方法虽然想法大胆，但可以获得更高的收益。该方法的先进性和有效性均可通过仿真实验研究进行验证。