考虑电压越限的主动配电网分布式光伏接入能力研究

黄 劲，王晓文，张明理，潘星辰

（1.沈阳工程学院a.研究生部；b.电力学院，辽宁 沈阳 110136；2.国网辽宁省电力有限公司 经济技术研究院，辽宁 沈阳 110015）

对可再生能源的开发主要分为集中式和分布式。分布式电源具有离负荷近、装机容量较小、便于就地消纳的特点。由于分布式光伏的上述优点，所以它已成为可再生能源开发利用的一种重要发电方式。为了解决分布式光伏接入后的配网接纳问题，保证大规模分布式光伏的充分利用，主动配电网技术就是有效途径之一［1-3］。主动配电网技术对于合理利用清洁能源，优化能源结构，减少分布式光伏对配电网的不良影响，提高分布式光伏的接入能力具有显著意义。

本文阐述了分布式光伏接入带来的问题，对分布式光伏进行建模研究，分析了分布式光伏接入主动配电网的电压特性，利用PSCAD、EMTDC 仿真软件分析了分布式光伏接入主动配电网的能力和影响分布式光伏接入能力的主要因素。

1 分布式光伏接入带来的问题

1.1 电压分布问题

接入分布式光伏后，配电网便成为一个多电源结构，所以潮流大小、方向也会随之发生变化，同时对电压特性也会产生影响，造成电压不稳定以及电压分布发生变化［4-5］。

1.2 分布式光伏的接入容量问题

随着分布式光伏大规模接入主动配电网，分布式光伏的接入最大容量成了主动配电网面临的主要问题之一，安全合理的接入最多的分布式光伏也是当今研究的一大趋势［6］。

2 分布式光伏系统建模研究

光伏电池的等效电路如图1所示。

图1 光伏电池等效电路

对于理想的光伏电池，当条件恒定时，可以等效成为一个恒流源。由图1 可得出光伏电池的输出特性为

式中，Iph为给定光强下的短路电流。

式中，Isc为标准条件下（Tref=25 ℃，光照强度为1 000 W/m2）的短路电流；参数αT为在参考日照下的电流变化温度系数。

式中，Irs为额定温度条件下二极管反向饱和电流；n为二极管影响因子；Eg为光伏电能带宽度；q为电荷常数，通常为1.60×10-19；k为波尔兹曼常数，通常为1.38×10-23。

在实际建设的光伏发电系统中，由于单个太阳能电池或组件的输出功率较小，因此需将单个太阳能电池或组件通过串并联形成光伏阵列，以满足大容量光伏发电系统的发电需求。由Nc个组件串联，Nb个组件并联的光伏阵列的电流特性方程为

由式（4）、（5）可以看出：光伏阵列输出的电流I与输出的功率P、输出电压V有关。

目前已并网发电的大型光伏电站均采用不可调度式并网光伏发电系统。不可调度式并网光伏发电系统由光伏阵列、并网逆变器及连接组件等组成，其示意图如图2所示。

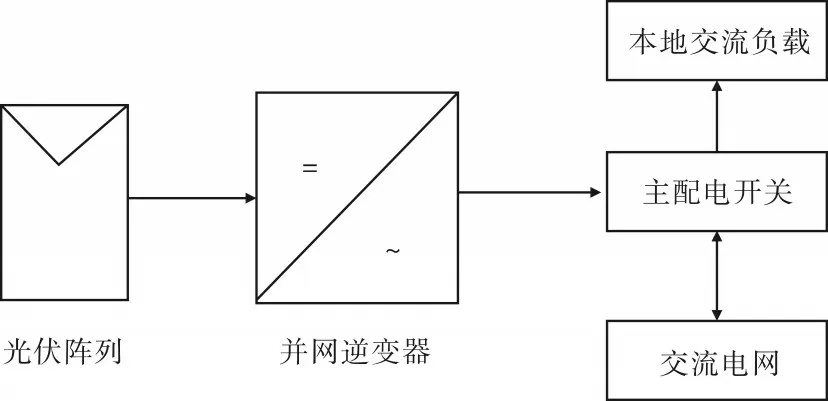
图2 不可调度式光伏发电系统

3 含分布式光伏的主动配电网电压特性研究

以图3 所示的简单主动配电网系统为基础，研究分析电压特性。

图3 含分布式光伏的主动配电网系统

3.1 系统电源作用下线路的电压降落

在系统电源单独作用时，主动配电网线路中任意j点的电压降表示为

式中，△Usj-为由任意点j之前的负荷造成的电压降；△Usj+是由任意j点后的负荷带来的电压降。

可得

最后可得到配电网线路的电压降：

式（9）表示的是系统电源作用下的j节点与系统电源点之间的电压降落。

3.2 分布式光伏独立作用下电压降落

分布式光伏单独作用时，先将主动配电网的系统电源侧短路，同时线路阻抗远远小于负荷阻抗，所以电压降主要表现在分布式光伏接入点到系统电源之间（i之前）；而对于i点之后的线路，对电压降落没有直接影响，但由于分布式光伏的接入，可能间接的抬高电压，设分布式光伏引起的电压降落为负，则有

所以，分布式光伏的接入一定会使配电网接入点处的电压得到抬升。

3.3 分布式光伏和系统电源共同作用下的电压计算

根据叠加定理得：

简单配电网系统的电压降为

若设此简单主动配电网系统的端电压为u0，则线路中任意j点的电压为

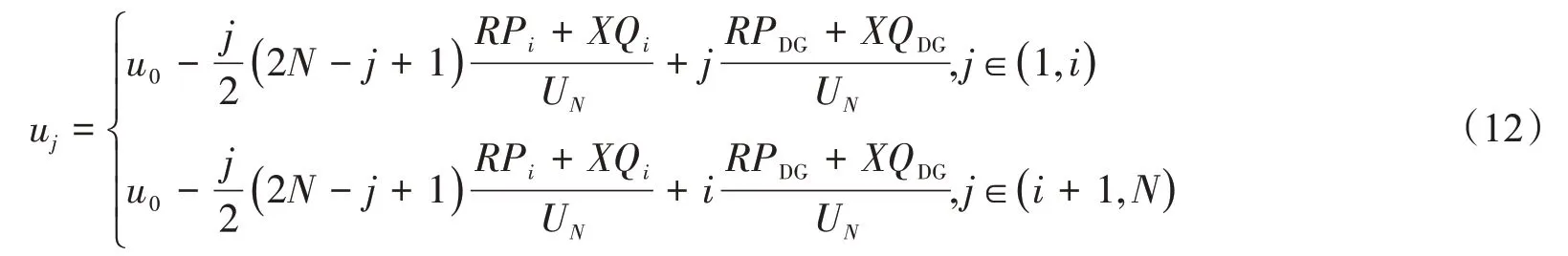
从式（12）可知，电压分布与接入位置i、接入容量等有关，由于功率因数决定了有功无功比例，所以它也是影响因素之一。

3.4 不同接入位置的主动配电网的电压分布

将式（12）进行简化，得到式（13），其中节点i为分布式光伏的接入点。

令X=(RPi+XQi)/UN，Y=(RPDG+XQDG)/UN。

以节点j的位置为变量，对式（13）进行具体的分析：

1）当j∈[1,i]，即分布式光伏在负荷之后时，可将ΔUj=j/2(2N-j+1)X-jY整理得

式（14）是关于j的二次函数，将此函数的数学意义结合实际情况进行分析可知，△Uj是单调递增的，当负荷所需功率大于分布式电源发出功率时，分布式光伏接入位置电压为前段线路的最低点，所以系统电压呈递减趋势。

2）当j∈[i+1,N]，即分布式光伏在负荷和发电机中间时，可将ΔUj=j/2(2N-j+1)X-iY整理得

由二次函数的意义可知，函数单调递增，分布式光伏接入会使电压最大值得以抬升，所以系统电压最高点在分布式光伏接入点处，在线路末端系统电压最低，系统电压呈先升高再降低的趋势。

3.5 不同功率因数主动配电网的电压分布

功率因数cosφ主要决定有功和无功的接入比例，以图3 所示的简单主动配电网系统为例，以相同容量不同功率因数在i点接入分布式光伏，研究其电压分布，i节点与i-1节点间的电压降落可以表示为

由式（16）可知，当分布式光伏只发出有功或发出有功和容性无功时，△Ui变小，令接入点i电压上升，若分布式光伏发出功率大于负荷功率，会产生功率逆流，致使i节点电压抬升；若分布式光伏输出有功功率但吸收感性无功功率时，△Ui的正负号不能确定，所以电压可能会减少，也可能会增大，这主要由分布式光伏和线路负荷的有功无功分布情况以及线路上X、R的关系决定［7-10］。

4 考虑电压越限分布式光伏接入能力

4.1 影响接入能力的因素

大规模分布式光伏接入后，会对系统稳定性产生影响，电压越限是限制分布式光伏接入容量的重要因素。同时，国家电网公司的光伏并网规定对并网光伏电站的输出电能质量做出了明确要求，所以电能质量也是影响分布式光伏接入能力的因素。因此，凡是影响分布式光伏并网的电能质量和系统稳定性的因素都决定了分布式光伏的接入能力［11-12］。

4.2 仿真分析

选取朝阳市金杖子66 kV 变电站作为仿真实例。金杖子变电站的负荷性质为农业生产和居民生活用电负荷。变电站规模为两台20 MVA 主变压器，配备长达20 km 的10 kV 电源线路，导线型号采用LGJ-240。电压检测点为3 个，1#测点在光伏接入端口10 kV 母线处，2#测点在距台区15 km处，3#测点在距离台区10 km 处。变电站系统如图4 所示。

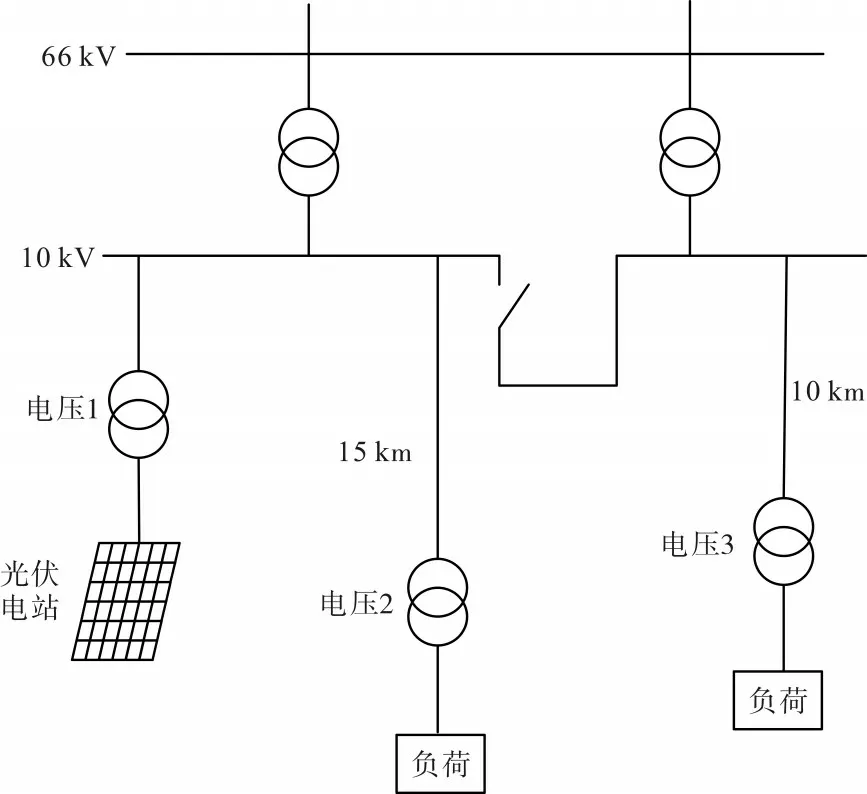
图4 朝阳市金杖子66 kV变电站系统

当负荷轻载，光伏电站输出功率为1 MW 时，仿真结果如表1 所示。通过仿真结果可以看出，10 kV 母线最高相电压瞬时值最大为8.3 kV，光伏电站最高相电压瞬时值为0.59 kV。单条10 kV 线路端口电压瞬时值比额定电压高出2%，电压有效值高出2%。光伏电站出口电压比额定电压高5.36%，在出力情况为1 MW 时，各个检测点电压并没越限。10 km、15 km、20 km 处的电压有效值几乎相同，且为10.2 kV。

表1 功率1 MW光伏电站电压分析

当负荷轻载，光伏电站输出功率为6 MW 时，仿真结果如表2 所示。通过仿真结果可以看出，10 kV 母线最高相电压瞬时值最大为9.7 kV，光伏电站最高相电压瞬时值为0.68 kV。单条10 kV 线路端口电压瞬时值比额定电压高出18.87%，电压有效值高出17%，光伏电站出口电压比额定电压高21.43%。可见变电站出线为20 km，负荷均为轻载情况下，光伏出力为6 MW与1 MW时相比，10 km、15 km、20 km 处的电压有效值越限情况明显，其中在20 km 处安装光伏电站的电压越限情况最严重，随着线路地缩短，电压逐渐降低。由此可见，线路越长对光伏电源接入越不利。

表2 功率6 MW光伏电站电压分析

光伏电站输出功率为6 MW，且20 km 线路所接为综合负荷（以5 km、1 MW、0.2 Mvar感性负荷，10 km、1.5 MW、0.2 Mvar感性负荷，15 km、1.2 MW、0.2 Mvar 感性负荷为例），变电站此时不进行无功功率补偿，仿真结果如表3 所示。通过仿真结果可以看出，10 kV 母线最高相电压瞬时值最大为7.95 kV，光伏电站最高相电压瞬时值为0.57 kV。单条10 kV 线路端口电压瞬时值比额定电压低2.57%，比电压有效值低4%。光伏电站出口电压比额定电压高1.79%。可见变电站出线为20 km，负荷在4.3 MVar 情况下，与负荷轻载时相比，10 km、15 km、20 km处的电压有效值出现低电压情况。

表3 综合负荷且功率6 MW光伏电站电压分析

通过仿真结果可以看出，配电台区光伏接入容量，即台区允许光伏出力大小由诸多因素决定，与潮流变化、线路长短、台区无功补偿量以及负荷特性等因素均有关系。

5 结论

本文通过提出分布式光伏接入带来的问题，对分布式光伏进行建模，分析分布式光伏接入后配电网电压特性，利用PSCAD 软件仿真研究分布式光伏接入能力，从求取结果可以看出，各节点光伏最大接入容量达到极限值时，其限制因素主要是满足系统电压失稳判据，也就是说系统的电压稳定性是决定光伏电站最大接入容量的主要因素。由此可知，为提高电网所能接纳的光伏最大接入容量，需提高电网在稳定和扰动两种情况下的电压稳定性。针对这些问题可采取如下措施以提高电网所能接纳的光伏最大接入容量：

1）优化光伏接入后系统的运行方式与网架结构，提高系统稳定性。

2）研究新型的光伏并网逆变器及并网控制策略，如并网逆变器控制策略采用并网点电压恒定控制而非功率因数控制，为系统电压稳定提供支持。

3）光伏接入容量和出力情况与负荷性质和大小密切相关，在电压不越限情况下，负荷越大，接入的光伏功率越大。为了解决高电压问题，可以利用主动配电网随时监测线路电压和负荷情况，动态调节光伏出力，以满足动态电压的要求。

4）在光伏电站接入动态无功补偿装置，如SVC、STATCOM等，调节系统电压。