半潜平台定位推进器激振力仿真方法及应用研究

韩华伟， 张媛， 王树青， 徐芹亮， 王娜

(1.中国海洋大学 山东省海洋工程重点实验室，山东 青岛 266100； 2.烟台中集来福士海洋工程有限公司，山东 烟台 264670)

定位推进器和柴油发电机组等旋转设备的运行极易引发半潜式平台结构的振动响应，过大的振动响应对平台结构造成伤害的同时也影响船员的健康。在平台设计初期进行振动响应预报具有提高平台设计建造效率、节省减振改造成本等优势，是平台设计流程中不可缺少的环节。其中定位推进器由于其激振力预报缺少参考，且激励范围难以确定等原因，大大制约其振动响应预报的准确性，因此开展定位推进器激振荷载的仿真模拟意义重大。

目前常用的推进器激振力预报方法有：理论计算、近似计算、实测方法和计算流体动力学分析(CFD)，但针对半潜式平台定位推进器，前2种方法的参考资料较少，常规的半潜式平台振动响应分析中的加载设置通常以实测荷载为主。推进器激振力都是以同类或类似型号实船的实测值作为输入，但由于测量误差和其他激励荷载影响等缺点，仍然难以满足要求。 因此推进器激振力的研究通常以数值模拟为主。针对螺旋桨激振响应预报问题，国内外学者主要对潜艇和舰船做了研究：付建等[1]利用有限元和边界元分析比较了螺旋桨激振力3个方向分力(轴向、横向、垂向)分别以及同时作用时引起的船体结构振动与水下辐射噪声，发现3个方向激振力同时作用时船体最大辐射声功率出现在叶频处，主要由横向力引起，其次是轴频处，主要由轴向力引起。Kinns等[2-3]建立了潜艇结构简化模型，在此基础上分析螺旋桨轴向力和波浪荷载对模型产生的响应。王蒙蒙等[4]提出计算空泡螺旋桨诱导的船体表面力新公式,预报了4条船的表面力并与国外有关方法进行比较，缩小了预报误差。

随着计算机技术的高速发展，第26届国际拖曳水池会议对CFD应用进行了的说明，认为CFD可以满足工程应用[5]。粘性流体CFD计算的控制方程是N-S方程，主要的湍流数值模拟可以分为直接模拟数值方法(DNS)、大涡模拟方法(LES)和雷诺平均方法(RANS)。其中RANS方法的核心是求解时均化近似的N-S方程来取代瞬时的N-S方程。因此，RANS方法在组合推进器、激振力预报和螺旋桨设计等问题上具有广泛的应用。文献[6-12]使用RANS方法对船用普通螺旋桨性能进行了研究，并通过实验验证了数值模拟的准确性。李亮等[13]采用混合网格技术，利用RANS方法和VOF模型，对计及自由液面的KCS船桨舵一体系统开展了螺旋桨激振力数值预报分析。丁科等[14]通过RANS和VOF方法，求取考虑只有叶面的“船+桨”系统的船用螺旋桨激振力，模拟了E779 A桨的敞水性能和考虑自由液面的裸船体的总浮力。王恋舟等[15]基于RANS方法以KCS船和KP505桨作为研究对象，采用六自由度运动模型和叠加旋转模型，进行了不同状态下的数值自航实验，分析获得准确度更高的分析模型。Ye等[16]对空气含量对空泡螺旋桨诱导的脉动压力影响进行实验研究，对螺旋桨空泡和船体脉动压力进行了测量。王丽楠[17将流域分为小域、中域和大域，并设置不同网格尺寸，最大尺寸为螺旋桨直径的5倍，以降低壁面效应影响。

由前述文献综述可以看出，现有研究一般都是针对船用螺旋桨的数值模拟，且由于计算时间长等因素并不适合工程应用。此外，全回转推进器的结构形式及导流罩不同于一般船用螺旋桨，其对外围流场影响较大，使得半潜式平台推进器的结构仿真模型及流场分布更加复杂，实测验证更加困难。

本文以准确预报定位推进器激励下某半潜式钻井平台结构振动响应为目的进行工程应用研究，首先基于CFD方法模拟分析单个定位推进器的激振力时程与力矩的频域曲线，同时对半潜式平台进行实船测试，获得定位推进器实测加速度的时频域曲线。然后进行振动响应预报研究，基于ABAQUS软件建立半潜式平台的有限元模型，分别将模拟荷载与实测荷载作为激振源，预报平台结构的强迫振动响应。最后通过响应对比分析，验证了模拟荷载方法的准确性，同时获得结构在定位推进器激励下的响应规律。

1 数值模拟

1.1 模型建立

以供应商提供的推进器参数为基础，建立推进器完整工程化应用分析模型。推进器型号为UUC405FP，4叶桨，盘面直径3.8 m，叶片扩比0.657，转动惯量(水中)5 795 kg·m2,总重量为6.575 t。单个叶片的空间投影如图1所示。

图1 实际切面展开尺寸Fig.1 Unfold dimension of practical section

基于推进器桨叶型值给出的空间点绘制每个切面空间轮廓线，形成4片桨叶组合模型，并通过拓扑结构关系在FLUENT前处理软件GAMBIT中得到共线的整体结构，同时考虑全回转推进器导流罩和导管的影响，建成如图2所示的推进器模型。

定位推进器的整体模型包括推进器结构和流体区域，如图3所示。流体区域分为旋转域和静止域，推进器进出口2个面是流体区域的分割依据。将桨叶、导管内部和相连桨毂所在的流域设置为旋转域，剩余部分为静止域。流体区域设置为圆柱形，尺寸设置为螺旋桨直径的4倍[13]，能较好地消减边界影响。其中流域上方的平板用于模拟实际推进器上方的舱底结构。为考虑尾流的影响，设置推进器后的流域尺寸大于来流方向流域，前后尺寸比例为1∶3。

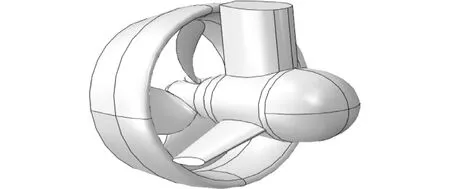
图2 推进器结构模型Fig.2 Thruster structure model

图3 螺旋桨激振力计算模型Fig.3 Thruster exciting force calculation model

1.2 网格划分

在满足工程设计精度和计算效率的基础上，2个流域分别划分网格，由于网格剧烈变化，旋转域采用非结构网格，最大网格尺寸20 mm。静止域采用Hexa-Dominant体网格，最大网格尺寸30 mm，螺旋桨表面网格20 mm。2个流域通过共面接口来进行能量交换，再通过网格导入，即可得到完整的计算模型。旋转域网格和静止网格如图4所示。

图4 流域网格分布Fig.4 Mesh distribution of Fluid

网格变形和重生注意以下方面：通过smoothing控制体网格更新和Local Cell控制边界体单元；边界单元更新通过Local Face控制；interface面通过Region Face控制更新区域面单元，旋转域内体网格及interface会同步更新，解决了出现负体积的情况。

1.3 边界设置

基于雷诺时均Navier-Stokes(RANS)控制方程来描述不可压流体的三维非定常流动、连续方程、动量方程、运输方程、Boussineq应力[12]，并选用RNGk-ε湍流模型封闭RANS方程。由于半潜式平台的浮箱在移航和正常作业情况下均浸没于水下，且平台在移航工况下的航速较低，因而在数值模拟中忽略自由液面和船体阻力的影响。

边界条件设置：入口位置设置为来流均匀的速度入口，速度大小根据实际工况得到；出口位置设置为outflow形式的出口条件，圆柱形的边界设置inflow为零，模拟无反射边界条件。计算时长大于2个旋转周期，以稳定计算后的时间开始计算，时间步长设定为10-4级，确保得到稳定的计算结果。

图5 桨叶面与叶背表面压力分布Fig.5 Pressure distribution of blade surface and back surface

1.4 流场分析

定位推进器激振力按照激振频率的不同主要有2种形式：轴频激振力和高频激振力(轴频和叶频、倍叶频)。其中，轴频激振力是由于推进器的制造误差导致推进器受力不平衡引发的，高频激振力是由不均匀流场引起的，激振频率等于轴的转动频率乘以桨叶数或者桨叶数的倍数。研究中认为推进器制造无误差，因此不存在轴频力，仅考虑叶频以上的高频力。当推进器在流场中工作，各桨叶的攻角在任一瞬间都不相同，其所产生的推力和遇到的旋转阻力也不相等，从而引发轴承力，表现为周期性变化的纵向推力、横向力和垂向力及3个方向的力矩，同时引发浮箱底部的垂向表面力。轴承力以纵向推力和纵向力矩最为显著，表面力则主要以垂向为主，因此在计算中只关注纵向和垂向的激振分量。分别将如图6所示的叶面、叶背的盘面压力差和桨叶的脉动压力沿不同作用表面和方向进行积分可以得到轴承力和表面力在各方向上的分量。

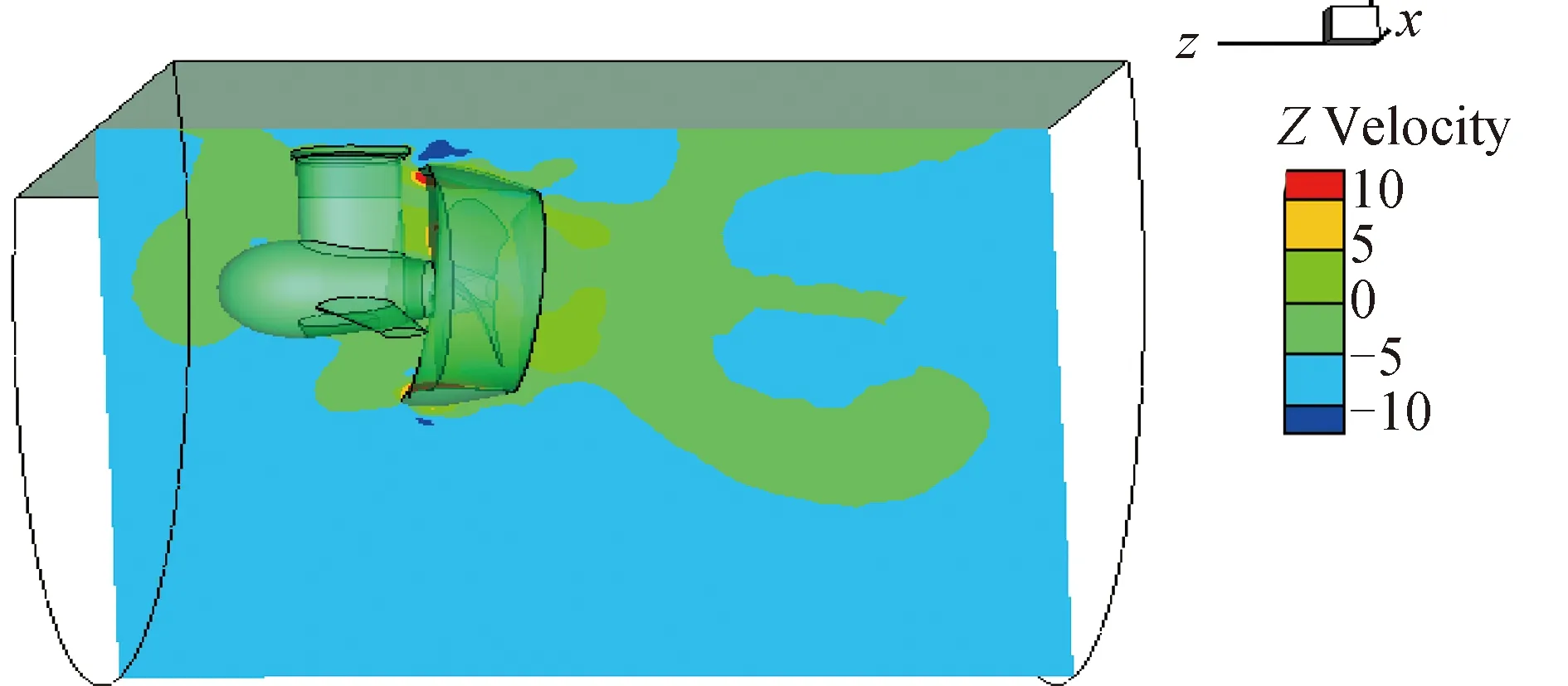
图6 流场的流速分布Fig.6 Velocity distribution of flow field

本研究模拟荷载考虑了推力、力矩和表面力的影响。，从如图6所示的流线以及压力的分布来看，推力及力矩作用位置集中在推进器与平台下浮箱的连接基座位置，同时推进器的尾部及导管的外部产生了明显的压力聚集区和负压区，即为表面力作用位置，因此确定推进器激振力荷载的施加位置为基座和导管外部区域。

1.5 仿真激振力计算

由于半潜式平台在移航工况下推进器转速较大且运转时间长，因此针对该工况下的推进器满功率运行状态进行模拟。由于设备在实际情况中与理想状态存在差异，导致推进器的转速不能保持恒定，在模拟时采用最大转速161 r/min进行计算，对应的轴频为2.68 Hz，叶频为10.72 Hz。经过FLUENT软件计算得到推进器各结构部分表面压力时域曲线。由于垂向力(表面力和轴承力的垂向分量)和纵向力(轴承力的水平分量)是对结构影响最为显著，在分析时对结构部分的力进行垂向和纵向积分处理，累加得到推进器激振力的时域脉动曲线，然后通过FFT变换对推进器激振力曲线进行频率成分分析。敞水条件下推进器的水动力计算中，其前方来流的不均匀性主要由螺旋桨前方支柱引起，因此数值计算中得到的螺旋桨水动力载荷(3个方向)出现规律性的谐波特性，其频率为螺旋桨的一阶叶频。

CFD数值模拟的结果如图7所示，其中包括垂向和纵向激振力和力矩的频域曲线。通过结果可以看出，纵向力和力矩频域曲线在轴频(2.6 Hz)、叶频(BPF 10.72 Hz)、倍叶频(2BPF 21.7 Hz、3BPF 32.1 Hz、4BPF 42.8 Hz等)处出现峰值，激振力幅值从低频到高频总体呈现降低的趋势。除此之外，纵向力和力矩在半叶频(0.5BPF 5.36 Hz、3.5BPF 37.45 Hz)处也有峰值，说明推进器在转动的过程中引发流场的不稳定导致偶数叶片的推进器的两个叶片同时经过高流速区时出现半叶频振动。与纵向力和力矩相比，垂向力和力矩的峰值较多且幅值大小相当，原因是垂向力和力矩主要由表面力组成，容易受到不稳定流场的影响引发多种倍频下的激励。通过对4个频域曲线的幅值分析可以看出，作为平台推进力的纵向分量激振程度最为显著。需要注意的是，由于CFD计算中忽略了实船定位推进器基座的弹性安装，为了计算方便采用刚性的边界和定航速的分析方法，这些简化会对计算结果有一些影响。

图7 推进器载荷曲线Fig.7 Exciting forces of thrusters

2 实测振动响应分析

2.1 推进器振动响应测试

为对比评估推进器的CFD仿真结果，在某半潜平台实船移航工况下对推进器基座结构进行振动测试实验。实验过程中平台设备开启情况如表1。

表1 模拟移航工况下主要设备开启情况Table 1 Main equipment status in transit

试验时海域水深51 m，约为平台移航工况吃水的5倍，以尽量减少海床的影响。采用加速度传感器，吸附于推进器基座结构处，在推进器最大功率运行平稳时进行振动加速度测试。测试数据经傅里叶变换得到推进器基座结构加速度的频域载荷。

由于实船测试的数据为推进器基座处结构的加速度，无法直接对比验证CFD仿真计算得到的激振力。因此通过平台结构模型的振动响应来验证全回转推进器激振力CFD仿真的可靠性。选取推进器实测数据0～50 Hz以内的部分作为输入载荷，其垂向加速度荷载曲线如图8所示。

2.2 推进器基座振动响应分析

从图8推进器基座振动响应的频域数据来看，其峰值分别出现在10.25 Hz(第1峰值,叶频)、25.25 Hz(第3峰值)、31.5 Hz(第2峰值，3倍叶频)，与CFD仿真得到的纵向力/力矩激励峰值频率(10.25 Hz、25.25 Hz)基本吻合。

图8 实测输入数据Fig.8 Measured data

3 振动响应预报分析

3.1 振动响应结构模型

为评估全回转推进器的激振力工程化模拟方法的可靠性，研究推进器激振力对半潜式钻井平台整体结构的影响，进行振动荷载输入下的某半潜式钻井平台结构振动响应研究。该平台主尺度为：106 m×74 m×56 m，浮筒底部对称布置6台全回转推进器。由于定位推进器最大振动常出现在平台的移航过程中，因此选择吃水10.1 m的移航工况作为研究重点，该工况下平台自重为32 600 t，航速为10 kn。

图9 实船照片Fig.9 Real ship picture

首先在ABAQUS软件中建立如图10所示的平台完整模型，含393 549个单元(其中：线性梁单元147 775个，四边形壳单元232 662个，三角形壳单元13 112个)及214 745个节点。

图10 平台总体模型Fig.10 Platform model

3.2 激振力施加及响应计算

由于CFD仿真计算得到的激振力位于推进器轴心处，载荷施加点为图11中设置的6个参考点，以图7得到的螺旋桨CFD仿真激励载荷为输入条件对上述平台进行有限元分析，得到整体结构响应。

4 对比分析

基于相同的平台模型，分别施加CFD数值模拟分析得到的激振力荷载和实测的基座处激振加速度载荷进行振动响应的对比分析。然后截取第1.5节中计算结果的稳定阶段，按照不同激励方向进行设置。由于平台甲板结构的固有频率接近叶频，因此以叶频下的结构振动响应作为主要研究内容。

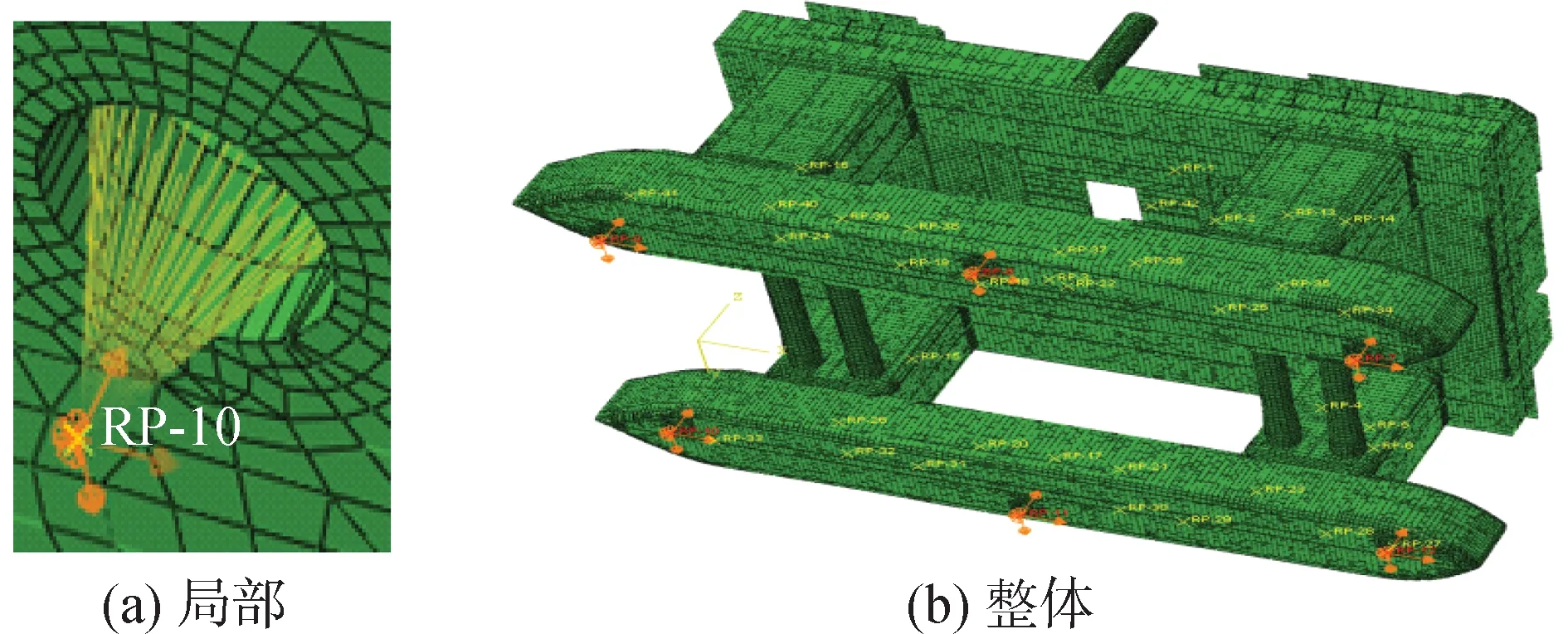
图11 CFD仿真载荷加载Fig.11 CFD simulation loading

实测激励载荷位于推进器基座面板，以图8螺旋桨测试数据为输入条件，施加在如图12所示面板轴心位置，对同一平台进行有限元结构响应分析。

在模型中施加的模拟荷载考虑了推力、力矩和表面力的影响。由于2种载荷的峰值均出现在叶频(10.72 Hz)处，且要比其他频率的力明显大，因此，将对比的频段设定在叶频处。对比区域选择半潜式钻井平台上层建筑生活区2层甲板和甲板盒上层甲板，即如图13所示的主甲板、01、02甲板。图14～16为实测振动加速度和CFD激振力分别作为输入下，3个甲板区域的计算结果在10.72 Hz下的响应。

图12 实测载荷下的激励响应Fig.12 Response with measured input

图13 选取甲板示意Fig.13 Schematic plan of deck

图14 02甲板振动速度响应云图Fig.14 Vibration velocity respond cloud chart of 02deck

图15 01甲板振动速度响应对比Fig.15 Vibration velocity respond cloud chart of 01 deck

图16 主甲板振动速度响应对比Fig.16 Vibration velocity respond cloud chart of main deck

通过图14～16实测数据和CFD模拟数据作为荷载的响应结果对比可以看出，实测荷载和CFD荷载的振动响应云图相似度很高且响应值非常接近，但实测响应值均高于模拟荷载的响应值，原因是平台浮箱中其他设备的影响。除了主甲板以外，其他所有结构在叶频下的振动速度响应幅值均高于10.13 Hz下的响应。分别对比同种荷载下3个甲板的振动速度可以发现，从低到高的3层甲板的振动响应呈上升趋势，这说明越靠近平台顶部结构，推进器振动影响越显著。出现这种情况是由于主甲板作为甲板盒结构的组成部分，具有较高的结构强度和整体性，固有频率高于叶频，2个频率下均没有发生结构的整体振动，只出现局部响应。相反，01、02甲板振动范围较大，且峰值较高，原因是2个甲板位于平台上层建筑，结构较为独立，且局部固有频率与轴频相近。如图17所示，主甲板在2种频率下的振型和响应值有微小差距，产生这种现象的原因是实际情况下推进器的精度与理想情况有差异，同时受到实船测试时不均匀流场的影响，导致最左侧的推进器产生额外的纵向力，传递至甲板导致靠近月池附近的结构振动响应与CFD荷载的计算结果有一定差异。

表2 模拟实测对比表Table 2 Comparison of simulation and test result

通过以上分析可以看出当目标平台在移航工况下，定位推进器转动会引发结构在叶频下的大范围振动响应，且越靠近平台顶部振动响应越显著。虽然2种荷载的计算结果略有差异，但除了主甲板在10.13 Hz下的响应受纵向力的影响以外，差异率均在15%以内，可以验证CFD方法计算半潜式平台定位推进器激振响应的工程应用的可靠性。

5 结论

1)提出了一种工程化的全回转推进器激振力的CFD数值模拟方法，并通过实船测试方法获得推进器的激励荷载，分析得到2种荷载激励下平台结构的振动速度云图，通过对比分析响应云图验证了CFD模拟的工程应用可靠性。

2)通过数值分析得到深水半潜平台在全回转推进器激励下的整体结构响应，基于对振动响应数据的分析，获得平台结构在推进器激励下的振动响应规律。