海冰与柱状结构作用的近场动力学数值模拟

贾宾， 王庆， 李文颉， 王键伟

(1.哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001; 2.中国船舶重工集团公司 第七〇三研究所, 黑龙江 哈尔滨 150078)

在渤海等覆冰海域，海冰会受风力、潮流力等作用发生漂移，在与柱状结构作用的过程中，海冰可能出现劈裂、挤压以及屈曲等破坏模式，其中挤压破坏最为常见。同时，此作用过程中极易形成交变载荷，引发结构振动。当前对于这种振动的机理解释大致可分为2类观点：1)认为冰激振动是一种强迫振动，实质是一种共振现象，与冰的破坏长度有关[1]；2)认为冰激振动是一种自激振动，实质在于能量供给与耗散之间的平衡关系。典型的自激振动模型是Maattanen[2]提出的负阻尼模型。

海冰与海洋结构相互作用的研究主要有理论方法、试验方法和数值模拟3种方法。数值方法凭借其应用灵活、成本低廉且效率高等优势，应用逐渐趋于广泛。其中，在有限元(FEM)方法应用领域，Martonen等[3]应用ANSYS对层冰与刚性锥体结构的作用进行了非线性有限元模拟，其中冰的破坏采用多面失效准则判断；Hilding等[4]应用内聚力单元法对冰与直立结构的相互作用进行了研究；武文华等[5]应用LS-DYNA计算了海冰与JZ20-2NW北高平台的相互作用过程中的动冰力和平台振动响应；龚榆峰等[6]应用ABAQUS的UEL平台开发出模拟失效的海冰单元，通过冰排与斜坡、圆锥结构相互作用算例进行了验证。而在离散元(DEM)方法应用领域，Paavilainen等[7]运用二维DEM方法模拟了冰与斜板作用下破碎、堆积现象，研究了作用过程中冰载荷和碎块形状特点；Lau[8]运用三维离散元方法模拟了冰排与锥体桥墩的相互作用，并同模型试验结果进行了对比验证；狄少丞等[9]基于GPU并行算法，根据梁单元理论构建海冰粘结模型，模拟了海冰与直立、锥体等平台结构的相互作用；邵帅等[10]采用DEM-FEM耦合算法模拟冰-结构相互作用，采用DEM模拟海冰的破碎，同时运用FEM计算平台结构的振动响应。

近场动力学(peridynamics，PD)理论由美国的Silling教授提出，并给出了相应的数值算法[11-12]。与经典连续介质力学不同，近场动力学基于非局部作用思想，采用积分型控制方程进行求解。其避免了传统数值方法中连续性假设和求解偏微分方程的困难[13]，在求解材料的裂纹扩展等非连续性问题上优势较为明显，在混凝土、复合材料等破坏问题的分析上取得了良好的效果[13]。

本文采用键型近场动力学方法(bond-based perdynamics)，模拟了海冰与柱状结构的相互作用过程。通过建立PD模型，同时考虑结构振动的影响，将单自由度振动方程加入到结构的位移计算中，求解相互作用过程中冰载荷和柱状结构的振动响应，将结果同文献[14]中离散元方法的计算结果进行对比以验证其合理性。讨论分析了桩径和冰速等参数对冰载荷和结构振动响应的影响。

1 近场动力学理论

如图1所示，对于某一时刻t下占据空间区域R的物质体，其动力学控制方程为：

(x′-x)dVx′+b(x,t)

(1)

式中：ρ为材料密度；f为物质点x与物质点x′之间的“力密度函数”；u代表物质点的位移矩阵；Hx表示以物质点x为中心且邻域半径δ划定的近场范围；b为施加在物质点x上的体积力。

弹脆性材料的作用力密度f(η,ξ)可表示为[15]：

(2)

式中：ξ、η分别代表物质点对的初始相对位置和相对位移。

图1 近场动力学理论相互作用示意Fig.1 Schematic diagram of interaction in peridynamic frame

ξ=x-x′

(3)

η=u(x′,t)-u(x,t)

(4)

c为微弹性模量。对于三维问题的数值模拟[12]，有：

(5)

式中：K为体积模量；s为“键”伸长率[12]，为：

(6)

对于各向同性材料，当物质点对的“键”处于拉伸状态时，s>0；反之若为压缩状态，s<0。

而μ(t,ξ)为一用来表示“键”状态的标量。

(7)

式中：s0为临界伸长率。当“键”伸长率达到s0时，认为“键”发生断裂。反之则没有发生破坏。

此外，Silling还提出了描述物质点局部损伤程度的物理量[12]：

(8)

φ取值范围为0～1。当φ=0时，表明物质点保持完好状态；当φ=1时，说明该物质点与其近场范围内的所有物质点之间均不再存在相互作用。

在数值计算时，需将连续体在笛卡尔坐标系下离散为空间内的一系列物质点，同时将求解空间积分方程转化为求解有限和的形式。其基本方程为：

(9)

2 数值模型建立

2.1 海冰PD材料模型

海冰的力学性质易受温度、孔隙度、盐度以及加载速率等影响。如图2所示，应变率对海冰的压缩强度影响显著[16]。在海冰与柱状结构的相互作用中，当加载速率较低时，冰力呈准静态特点，海冰体现为韧性材料；当加载速率较高时，冰力呈随机性特点，海冰材料呈脆性破坏；而在中等加载速率下，冰力则呈稳态特性，海冰材料处于韧-脆转换状态[17]。考虑到本文算例中所选取的冰速，重点考虑海冰的脆性破坏，在计算模型中将海冰视为弹脆性材料，满足线弹性本构关系。

图2 海冰材料特性随应变速率的变化特征Fig.2 Characteristic variety of sea ice with strain rates

此外，海冰在较高应变率下的脆性破坏呈现出较明显的拉压异性。相关实验数据显示，冰的压缩强度一般为拉伸强度的3～5倍[18]，此处取sc=-4·st，其中st和sc分别为冰材料临界拉伸、压缩率。海冰的PD材料本构关系如图3所示。

图3 海冰材料本构关系Fig.3 Constitutive relation of sea ice

海冰发生韧-脆转换时对应的应变率约在1.0×10～3.0×10-3s-1[19]。根据文献[20-23]中渤海冰的相关实验数据统计发现，海冰在韧-脆转换范围内压缩强度极值近似为脆性区压缩强度极值的1.3～2倍。本文取韧-脆转换状态下海冰的临界压缩率为脆性状态下的1.8倍。

2.2 临界伸长率s0

近场动力学方法通过s0判定材料是否发生断裂，可由其与断裂面的能量释放率G0关系进行推导。

(10)

式中：E为弹性模量；G0可通过线弹性断裂力学进行推导[24]：

(11)

式中：KIC为断裂韧度，可通过实验测量等方法确定，以此建立s0与KIC之间的关系：

(12)

季顺迎等基于渤海海冰断裂韧度实验结果，归纳出断裂韧度KIC与温度T之间的拟合关系[25]：

KIC=-9.293T+76.366

(13)

2.3 接触模型

根据Parks等所述，计算物体间的接触力时需引入短程排斥力，以避免不同物体的物质点占据相同空间位置[15]。当两粒子间距小于短程排斥力临界范围dp时，粒子间相互排斥力密度函数fs为：

(14)

式中：p和i分别为来自不同物体上的粒子；cs为短程力常数。依据经验，

(15)

dp=min{0.9|xp-xi|,1.35(rp+ri)}

(16)

式中rp和ri分别代表粒子p和i的物质点半径。

2.4 桩腿振动模型

如图4所示，桩腿被简化为具有一定质量M、结构刚度K和阻尼系数C的振动结构，受海冰作用产生水平x方向的振动，满足单自由度振动的动力学方程：

(17)

式中Fc表示柱状结构与海冰之间的接触力。

2.5 计算方法

海冰粒子的运动采用向后差分法进行求解。在第n步时，

(18)

(19)

(20)

根据文献[12]，时间步长需满足:

(21)

图4 结构振动模型Fig.4 Vibration model of the structure

图5 数值模拟计算流程Fig.5 Flow chart of numerical simulation

3 结果与分析

3.1 参数选取

数值模拟主要参数取自文献[14]，如表1所示。海冰厚度方向划分3层粒子，粒子尺寸Δx约为0.087 m，取近场范围δ为3·Δx，时间步长Δt为1.0×10-4s。为体现海冰半无限宽特性并忽略边界的影响，除与桩腿发生接触的一面处于自由状态之外，其他三面均作刚固处理。取桩腿移动的方向为坐标系x轴正向，计算模型如图7所示。

图6 “键”力计算方法Fig.6 Computation method of the bond force

表1 计算参数Table 1 Calculation parameters

图7 海冰与柱状结构相互作用的数值模型Fig.7 Numerical model of the interaction between the sea ice and cylindrical structure

3.2 计算结果

图8、9分别给出了黄焱等的海冰与柱状结构相互作用的实验现象以及本文数值计算得到的效果图。通过对比发现，近场动力学数值模型能够较为合理地反映海冰在此过程中的挤压破碎现象。

图8 海冰与直立桩腿相互作用的实验现象[26]Fig.8 Experimental phenomenon of interaction between sea ice and cylindrical structure[26]

图9 数值模拟可视化效果图(第21 400步)Fig.9 Virtual reports of the numerical simulation(step 21 400)

0.5 m/s冰速下柱状结构所受水平冰载荷时程变化如图10(a)所示。此外，增加采样频率，在图10(b)中给出了4.8～6 s内的冰载荷细节。根据图像，水平冰力呈无规律的加、卸载随机性特点。计算得到的柱状结构振动响应时程如图11所示。

图10 水平冰力的时程变化Fig.10 Horizontal ice force during the simulation

图11 振动响应的时程变化Fig.11 Vibration response of structure during the simulation

表2给出了在相互作用过程中计算得到的水平冰力、柱状结构振动位移及振动加速度的数据分析结果，同时与文献[14]中计算得到的结果进行了对比。经分析，通过PD方法计算得到的冰载荷与柱状结构的振动响应与文献[14]中的计算结果吻合较好，验证了计算方法的合理性。

表2 PD计算结果与文献[14]计算结果的对比Table 2 Comparision of results calculated by Peridynamics and from literature [14]

4 参数影响分析

4.1 桩径对水平冰力与振动位移的影响

对1.2 m、1.6 m和2.4 m桩径下海冰与柱状结构相互作用进行了数值模拟，冰速仍取0.5 m/s，其他计算参数不变，同3.1节所述。水平冰力与结构振动位移计算结果分别如表3～4所示。

表3 不同桩径作用下水平冰力的计算结果Table 3 Horizontal ice forces with various diameters of cylindrical structure

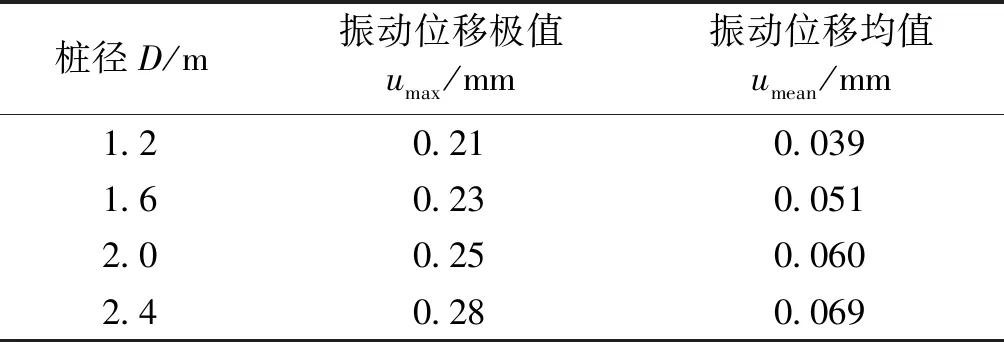
表4 不同桩径作用下结构振动位移的计算结果Table 4 Structure vibration displacements with various diameters of cylindrical structure

如图12(a)所示，水平冰力整体随桩腿直径增大呈增加趋势。考虑当桩径较大时，两者间接触区域较大，导致了随机冰力的增大。如图12(b)所示，对比不同桩腿直径下结构的振动响应发现，结构振动位移极值和均值均随桩径增加而增加。考虑桩径增大提升了冰力值总体水平，增大了振动系统外力输入，进而导致了振动响应的增大。

图12 桩径的影响规律Fig.12 The effect of diameter of cylindrical structure

此外，如图13所示，计算发现Fmax/Fmean随径厚比D/h增大逐渐减小，与Sodhi的实验结果一致，符合Kry提出的冰载荷极值与均值随着结构宽度增加逐渐接近的观察结果[26]。

图13 Fmax/Fmean与D/h的关系Fig.13 Ratio of maximum force to mean force Fmax/Fmean versus the ratio of diameter to ice thickness D/h

4.2 冰速对水平冰力与振动位移的影响

分别取冰速0.2、0.8和1.1 m/s进行计算，桩径仍取2 m，其他参数保持不变。水平冰力、结构振动位移计算结果分别如表5～6所示。

表5 不同冰速下水平冰力的计算结果Table 5 Horizontal ice forces with various moving velocities of sea ice

表6 不同冰速下结构振动位移的计算结果Table 6 Structure vibration displacements with various moving velocities of sea ice

如图14(a)所示，水平冰力总体随冰速增大而增大，但增速逐渐放缓，0.5、0.8和1.1 m/s下冰力均值十分接近。而冰速0.2 m/s时水平冰力极值较0.5 m/s时较高，与Sodhi和Morris的平板冰与刚性立柱结构接触实验结果具有一定的相似性[27]。如图14(b)所示，振动位移均值随冰速增大而增大，但极值却随冰速呈负增长趋势。通过对比各冰速下结构的振动位移时程曲线发现，0.8和1.1 m/s下结构振动位移曲线同0.5 m/s时类似，均呈随机性。但0.2 m/s下结构振动位移幅值持续维持在0.2～0.4 mm，且具有较明显的周期性特点，如图15所示。因此，认为在0.2 m/s冰速下柱状结构的振动为稳态振动。

图14 冰速的影响规律Fig.14 The effect of moving velocities of sea ice

图15 结构振动位移的时程变化(0.2 m/s)Fig.15 Vibration displacement of cylindrical structure during the simulation (0.2 m/s)

黄焱等[27]的实验结果显示，当柱状结构与海冰相互作用发生稳态振动时，结构振动位移主频与结构的自振频率近似。对0.2 m/s冰速下的柱状结构振动位移时程数据进行快速傅里叶变换(FFT)，计算结果如图16所示。由图可知，结构振动位移在频域上具有6.625 Hz的主频，与系统自振频率6.497 Hz相近，验证了结构发生稳态振动。

图16 结构振动位移频域分析结果Fig.16 Analysis results of structure vibration displacements in frequency domain

此外，计算了冰载荷极值与均值的比值Fmax/Fmean随冰速-厚度比v/h的变化关系，其结果如图17所示。

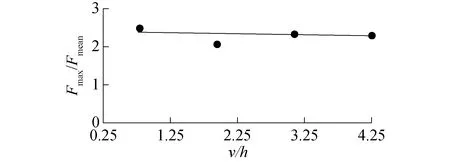
图17 Fmax/Fmean与v/h的关系Fig.17 Ratio of maximum force to mean force Fmax/Fmean versus the ratio of velocity to ice thickness v/h

由图17可知，Fmax/Fmean随着v/h增大呈微幅减小的趋势，这与Sodhi的实验结果相一致[27]。

5 结论

1)总体来说，海冰与柱状结构相互作用引发的水平冰载荷与桩径、冰速呈正相关关系。结构的振动位移随着桩径增大而增大，随着冰速增大而减小。

2)柱状结构发生稳态振动时，其结构振动位移具有较为明显的主频且与系统自振频率近似。

3)挤压过程中，冰载荷极值与均值的比值Fmax/Fmean随着D/h和v/h的增大逐渐减小，其中随v/h的变化幅度较小。