《方程的根与函数的零点》(第一课时)教学设计

冯鹏梅

一、教材分析

本节内容是人教A版数学必修1第三章“函数与方程”第一节的第一课时，本节体现了函数与方程、数形结合等重要思想，揭示了方程与函数之间的联系，同时为后面学习“零点存在性定理”、“二分法求方程的近似解”等内容打下基础。

二、教学目标

（1）知识与技能：

结合二次函数的图象，判断一元二次方程根的存在性及个数，从而了解函数的零点与方程的根的联系。

（2）过程与方法：

培养学生观察 、思考、分析、猜想，验证的能力，并从中体验从特殊到一般及函数与方程思想。

（3）情感态度与价值观：

在引导学生通過自主探究，发现问题，解决问题的过程中，激发学生学习热情和求知欲，体现学生的主体地位，提高学习数学的兴趣。

三、教学重难点

重点：体会函数零点与方程根之间的联系，掌握零点的概念。

难点：能够选择恰当的方法求函数的零点。

四、学情分析

学生已经学习过一次函数、二次函数、反比例函数、指数函数、对数函数的定义、图象、性质，会解一元一次方程、一元二次方程。初步认识过一元二次方程的解与相应二次函数的图像的联系.

五、教学方法

以问题为载体，学生活动为主线，以多媒体辅助教学为手段利用探究式教学法，构建学生自主探究、合作交流的平台。

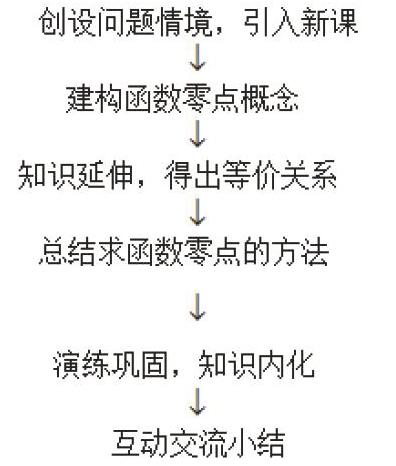
六、教学过程

七、反思与体会

现代教育心理学的研究认为，有效的概念教学是建立在学生已有知识结构基础上的，因此我在教学设计过程中注意了：

（1）在学生已有知识结构和新概念间寻找“最近发展区”;

（2）设法走出“轻概念，重练习”的误区，促使自己与学生一起走进“重视探究、重视交流、重视过程” 的新天地。因此教学设计时逐层铺垫，降低难度。由具体到一般，建立一元二次方程的根与相应的 二次函数的零点的联系，然后将其推广到一般方程与相应的函数 的情形。同时，恰当地使用多媒体，让学生直观形象地理解问题，了解知识的形成过程。

采用“启发—探究—讨论”的教学模式精心设置一个个问题链，给每个学生提供思考、创造、合作和探究的机会.

本节的教学设计本着让学生经历“创设问题情境——建构概念——探究定理——注重反思——拓展应用”的指导思想，让学生参与数学知识的发生、发展过程，提高他们学习数学的兴趣，成为课堂教学的主体。