等离子体与高功率微波相互作用中电子分布特性*

李志刚，陈宗胜

(国防科技大学 脉冲功率激光技术国家重点实验室， 安徽 合肥 230037)

等离子体是一种由大量自由运动的分子(或原子)、电子、离子构成的特殊媒质，其电磁特性与内部带电粒子的变化密切相关[1]。当高功率微波入射到等离子体中时，两者之间的相互作用明显。一方面，入射波在等离子体区域产生强电磁场，带电粒子在强电磁场的作用下产生加速运动，等离子体内能提高，内部碰撞反应、非弹性碰撞加剧，等离子体状态产生剧烈变化，内部电子密度、电子能量、重粒子密度不断增加；另一方面，等离子体的电磁特性也会发生较大改变，对入射波的损耗性能加剧，同时，当不断增加的电子密度达到电磁截止密度时，等离子体就会对入射波产生屏蔽作用，高功率微波无法透过等离子体区域[2-4]。

等离子体与高功率微波之间的相互作用可通过等离子体中带电粒子的变化表现出来，通常采用电子数密度进行表征[5]。为深入研究等离子体与高功率微波之间的相互作用，本文采用等离子体流体近似方法，利用COMSOL软件仿真分析研究了相互作用中的电子数密度和电子能的变化特性，着重分析了相互作用中产生的电子雪崩效应的变化过程，探究等离子体产生电磁屏蔽的作用机理。

1 基本理论

等离子体是由带电粒子构成的高度非线性组合体，想要精确描述等离子体的动力学行为，必须要对等离子体中的每个粒子进行轨迹跟踪和分析，但是，由于等离子体内部粒子数量实在太大，在实际研究过程中，这是无法实现的[6]。目前，只能根据不同条件和研究问题，采用不同的近似方法，对研究问题进行简化分析，本文采用流体近似研究方法对相互作用中的电子分布特性进行分析研究[7]。

流体近似方法是将等离子体等效为导电流体，采用经典流体力学和电动力学相结合的方法，研究等离子体与外界电磁场之间的相互作用，只用宏观参量来描述等离子体的物理特性，着重分析等离子体的整体行为，不考虑其中单个粒子的运动状态[8]。流体近似法主要用于描述等离子体的宏观运动，可通过求解流体力学方程组进行求解[9]。在等离子体与高功率微波相互作用中，高功率微波的传播过程可通过波动方程进行表征，等离子体内部粒子的变化作用可通过电子漂移-扩散方程和重物质传递方程进行计算分析。

1.1 波动方程

将等离子体作为特殊电介质进行分析，等离子体中的麦克斯韦方程为：

▽×H=jωε0εr·E

(1)

▽×E=-jωμ0H

(2)

可得波动方程为：

(3)

其中，E为电场强度，H为磁场强度，ω为入射波的角频率，ε0、μ0、k0分别为真空中的介电常数、磁导率和波数，εr为等离子体的相对介电常数，可通过下式求解：

(4)

式中，ωp为等离子频率，υ为电子碰撞频率，i为复数标号。

1.2 电子传递方程

在相互作用中，电子数密度的变化可通过电子传递方程来进行分析，可表示为：

(5)

Γe=-(μe·E)ne-De·▽ne

(6)

其中：ne为电子密度；μe、De分别为电子迁移率和电子扩散率；Re为电子源项，表征等离子体内部碰撞反应导致的电子的产生与消失，可通过下式求得。

(7)

式中，xj为j反应中碰撞粒子的摩尔质量分数，kj为j反应的反应速率，Nn为等离子体中总的粒子数密度。

1.3 重物质传递方程

在相互作用中，非电子粒子也会受到外加电磁场的影响，这些变化可通过重物质传递方程来进行分析，可表示为：

(8)

其中：ωk为第k种粒子的摩尔分数；ρ为气体密度；μ为平均流体速度；jk为第k种粒子的扩散通量，可通过下式表示。

jk=ρωkVk

(9)

(10)

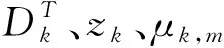
2 计算模型

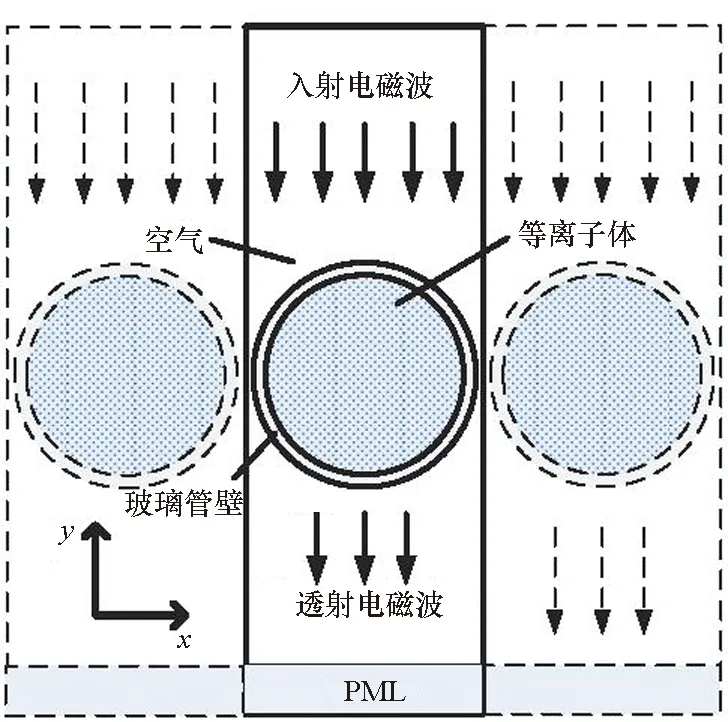
图1 等离子体与高功率微波相互作用计算模型Fig.1 Schematic diagram of the interactions between HPM and plasma

基于流体近似方法，本文采用COMSOL软件对波动方程、电子漂移-扩散方程和重物质传递方程进行求解，对高功率微波入射到等离子体中产生的变化进行分析[10]。计算模型如图1所示，模拟分析高功率微波对等离子体管阵列进行激励，等离子体层由左右延伸的等离子体阵列结构组成，电磁波由上边界入射传播方向为-y方向，经空气层和等离子体层，传输至完美匹配层(Perfectly Matched Layer, PML)后被完全吸收。入射电磁波的功率大小采用电场分量来表述，假设入射电磁波场强幅值为E0，频率为f，极化方向与等离子体管方向一致；然后，等离子体区域填充低气压氩气作为等离子体源体，相互作用中的碰撞粒子和反应在表1给出，等离子体区域气体温度设为T，气体压强为P。

表1 氩等离子体发生的碰撞反应

本文重点研究了等离子体与高功率微波相互作用中电子分布特性产生的变化。初始时刻，内部电子初始分布采用均匀分布，初始电子密度分别设置为1.0×1016m-3，初始电子能为3 eV，碰撞频率为5×109Hz，高功率微波频率选择 6 GHz，电场强度为2×106V/m，气体温度设为300 K，压强设为400 Pa，计算时间设置为0～0.01 s。

3 结果分析

3.1 电子数密度变化

3.1.1 数值分析

图2 等离子体与高功率微波相互作用中平均电子数密度的演变过程Fig. 2 Time dependence of the averaged electron density in the plasma of the interactions between HPM and plasma

图3 等离子体与高功率微波相互作用中电子变化速率的演变过程Fig.3 Time dependence of electron change rate in the interactions between HPM and plasma

图2给出了等离子体与强电磁脉冲相互作用中等离子体区域平均电子数密度的演化曲线，图3为电子平均变化速率的演变过程，图中横纵坐标均采用对数坐标表示。从图中可以看出，等离子体区域电子数密度发生剧烈变化，在计算时间(0～0.01 s)内，平均电子数密度从初始值1.0×1016m-3增长至8.0×1022m-3，变化范围近7个数量级。按照图中曲线变化趋势，电子数密度的变化过程在时间上可划分为四个阶段：

1)缓慢增长阶段(0 ～t1，这里t1=4.4×10-11s)，平均电子数密度由1.0×1016m-3增加至1.1×1016m-3，电子变化速率在10 mol/(m-3·s)以下。产生这种现象的原因主要有两个方面，一是这一阶段高功率微波入射时间较短，并且等离子体内电子数密度较小，等离子体对入射波的吸收能力较弱，因而只有较少的入射能量被等离子体吸收；二是等离子体具有很强的维持内部粒子平衡的趋势，初始时刻等离子体内部碰撞反应以弹性碰撞(反应1)为主，等离子体将吸收的电磁能量转化为自身内能，削弱外加电磁波对内部平衡的干扰，同时，吸收的电磁能量不足以激发更为频繁的非弹性碰撞反应，新生电子产生速率相对较慢，和熄灭速度基本保持一致。

2)雪崩增长阶段(t1～t2，这里t2=1.2×10-9s)，等离子体区域发生电子雪崩效应，在极短的时间内(< 1 ns)，平均电子数密度由1.1×1016m-3跃变至5.1×1018m-3，增长2个数量级，电子产生速率也由10 mol/(m-3·s)迅速增加至1.6×104mol/(m-3·s)。值得注意的是，在这一阶段内，当t=tc(这里，tc=5.0×10-10s)时，平均电子数密度值为4.6×1017m-3，与入射波(6 GHz)的电磁截止密度相一致。产生这一现象的原因在于：初始阶段，等离子体吸收电磁能量主要用于提高自身内能，大量电子的运动速度增加，由低能电子转变为高能电子，具备大范围发生非弹性碰撞反应的能量基础，持续的电磁能量输入，使得等离子体内激发碰撞(反应2)、电离碰撞(反应3、反应4)等反应突显、频繁发生，电子产生速率远远大于电子熄灭速度，大量的电子和激发态氩原子不断产生，同时，新生电子和激发态氩原子也会参与到内部非弹性碰撞反应中，产生更多的电子和激发态氩原子，循环往复，导致电子雪崩效应产生，等离子体中电子数密度急剧增加，直至初始阶段积累的高能电子基本消耗殆尽，电子雪崩增长才会结束。

3)振荡增长阶段(t2～t3，这里t3= 2.3×10-4s)，平均电子数密度由5.1×1018m-3振荡增加至7.6×1022m-3，电子产生速率有所减缓，由1.6×104mol/(m-3·s)逐渐减小为400 mol/(m-3·s)。这一阶段电子数密度的变化较为复杂，主要是下面几个因素导致的：一是在前一阶段，高能电子被大量消耗，电离反应4(电子与基态氩原子碰撞直接电离产生氩离子和新生电子)由于具有较高的能量壁垒(15.8 eV)，反应速率难以维持，导致等离子体电子产生速率减小；二是前一阶段在产生大量电子的同时，激发反应也产生了大量的激发态氩原子，这些激发态氩原子参与到反应5(电子与激发态氩原子碰撞电离产生氩离子和新生电子)中，电离反应5由于所需能量(4.24 eV)较少，在这一阶段更容易发生，这一反应能够在一定程度上维持电子的产生；三是电子数密度不断增加，会导致碰撞反应的发生概率也相应增加，同时等离子体可以将更多的入射能量转换为等离子体内能，参与到内部碰撞反应中，为电子的产生持续提供能量。

4)平稳保持阶段(t3～ 0.01 s)，等离子体区域平均电子数密度保持小幅增长，整体基本稳定保持在8.0×1022m-3，电子产生速率基本维持在700 mol/(m-3·s) 左右。在这一阶段，电子产生速率保持在较小的层次。产生这一现象的原因在于经过前面阶段的剧烈反应，高能电子和激发态氩原子被大量消耗，等离子体区域电子数密度大幅增长，单纯的外加能量输入难以维持频繁、剧烈的非弹性碰撞反应，等离子体内部逐渐达到新的平衡，内部反应趋于缓和，电子产生速率减缓。

3.1.2 空间分布

图4给出了等离子体中的电子数密度空间分布随作用时间的演变过程，整体来说，等离子体中电子数密度随计算时间不断增大。

(a) t=2.15×10-10 s (b) t=3.98×10-10 s (c) t=4.89×10-10 s

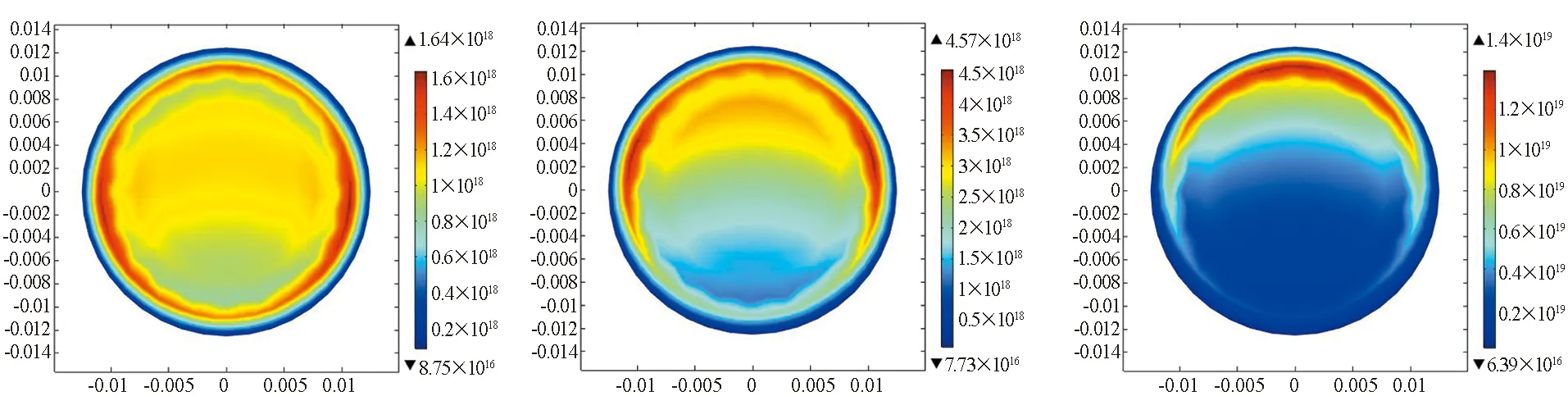
(d) t=5.99×10-10 s (e) t=7.35×10-10 s (f) t=9.03×10-10 s

(g) t=1.11×10-9 s (h) t=1.05×10-8 s (i) t=1×10-7 s

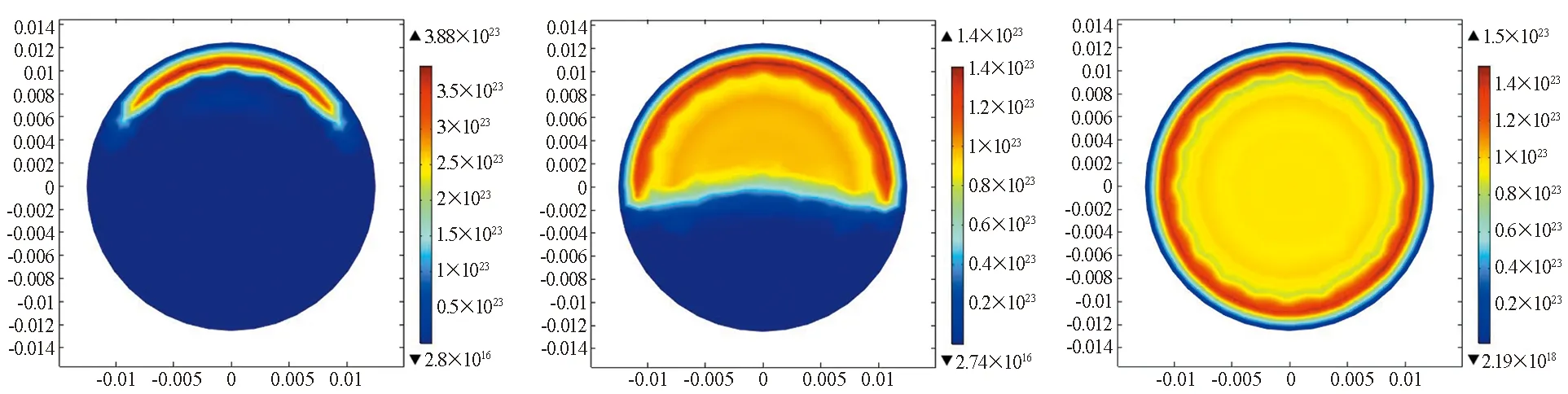
(j) t=1.1×10-5 s (k) t=1.05×10-4 s (l) t=0.001 s图4 等离子体与高功率微波相互作用中电子数密度空间分布的演变过程Fig. 4 Time dependence of the spatial distribution of the electron number density in the interactions between HPM and plasma

初始阶段(图中t=2.15×10-10～4.89×10-10s)电子数密度变化最明显的特征是整体均匀增长。这是由于等离子体区域初始电子数密度值较小，入射波能够在等离子体中传输，强电磁脉冲产生的外加电磁场将加速带电粒子运动，加剧内部碰撞反应的发生，尤其是非弹性碰撞反应，导致等离子体区域电子数密度急速增长。另外，从单幅图像对比来说，等离子体边缘区域的电子数密度增长速度要大于中心区域。产生这种现象的原因主要有两个方面：一是等离子体具有一定的电子数密度，带电粒子频繁地进行不同类型的碰撞反应，会对入射波产生一定的衰减，这样导致入射电场周边大中间小；二是柱状结构的等离子体类似于柱状电介质，能够改变入射波的电磁分布，会形成环绕柱状结构的电磁分布，由于等离子体具有一定的衰减作用，入射到等离子体中的电磁波能量会受到衰减，圆柱周边电磁作用强烈，电子碰撞反应更为剧烈。

在电子数密度快速增长阶段(图中t=5.99×10-10～1×10-7s)电子数密度峰值表现出向波源方向移动的趋势，并且电子数密度峰值越来越尖锐。从t=5.99×10-10s开始，等离子体区域下边缘处电子数密度增长减缓，与其他区域相比，电子密度值较低。这是由于等离子体两侧区域的电子数密度增加速率相对较大，电子数密度率先增长至电磁截止密度。这样，就会使得入射到等离子体下边缘区域的电磁能量大幅度减小，电子数密度增加减缓，出现下边缘区域电子数密度相比于其他区域较低的现象，电子数密度峰值开始向等离子体上边缘区域移动。另外，随着等离子体上边缘区域电子数密度进一步增加，透射到下边缘等离子体区域的电磁能量会进一步减小，碰撞反应速率进一步降低，下边缘区域的电子数密度增长进一步减缓，等离子体区域电子数密度峰值进一步上移。

在小幅增长、稳定保持阶段(图中t=1.10×10-5～0.001 s)，等离子体区域电子分布开始趋于均匀，电子数密度峰值降低。在前一阶段中，峰值位置大量的高能电子和激发态氩原子被消耗，等离子体区域频繁进行的非弹性碰撞反应趋于缓和，电子数密度增长减缓，同时等离子体区域存在较大的浓度梯度，上边缘区域的高浓度电子就会向下边缘区域漂移扩散，在下边缘区域碰撞反应，等离子体区域电子密度逐渐趋于均匀，最终达到新的内部平衡，入射波无法维持等离子体内电子快速增长，也无法对新产生的内部平衡产生破坏，等离子体吸收入射波提供的电磁能量，来维持正常的内部反应。

3.2 平均电子能

3.2.1 数值分析

图5给出了等离子体区域平均电子能量随时间的演变曲线。从图中可以看出：在0 ～t1时间内(这里，t1=5.0×10-10s)，平均电子能由3 eV快速增加到112 eV，在t1～t2时间内(这里，t2=1.2×10-9s)，平均电子能急剧减小，由112 eV减小至8 eV，在t2～t3时间内(这里，t3=2.3×10-4s),平均电子振荡减小至2 eV，而后保持稳定。值得注意的是，平均电子能达到峰值点的时间与电子数密度达到截止密度的时间相一致；平均电子能急速衰减结束的时间与电子数密度雪崩增长阶段的结束时间相一致。这一现象说明，直接电离碰撞是电子雪崩效应产生的主要反应。

图5 等离子体与强电磁脉冲相互作用平均电子能的演变过程Fig. 5 Time dependence of the average electron energy in the interactions between HPM and plasma

产生这一变化的原因为：初始阶段，入射波会在等离子体区域产生很强的电磁场，内部电子受到外加电磁场的作用产生加速运动，电子内能迅速增加，由低能电子转化为高能电子，平均电子能增加迅速。而后，等离子体内碰撞反应开始加剧，电子数密度也开始急剧增加，高能电子开始被消耗，当等离子体区域平均电子数密度达到截止密度时，等离子体开始对入射波产生屏蔽作用，电磁能量传输受限，平均电子能增加受到限制；与此同时，前期产生的高能电子会在剧烈的非弹性碰撞中被大量消耗，等离子体区域平均电子能急剧下降。当内部碰撞反应趋于缓和后，高能电子消耗减小，等离子体区域逐渐建立新的粒子平衡，电子数密度增加减缓，电子分布开始趋于均匀，平均电子能也逐渐趋于稳定。

3.2.2 空间分布

图6给出了等离子体区域电子能的空间分布随作用时间的演变过程。从图中可以看出，初始阶段，等离子体区域电子能表现为整体增长，由于外加电磁场分布的影响，电子能会出现边缘大中间小的现象，同时，随着电子数密度不断增加，等离子体上游区域的电子能增加速度要快于下游区域，电子能峰值向波源方向移动，开始时会出现两个峰值点，这是计算模型的对称结构产生的。

(a) t=2.15×10-10 s (b) t=3.98×10-10 s (c) t=4.89×10-10 s

(d) t=5.99×10-10 s (e) t=7.35×10-10 s (f) t=9.03×10-10 s

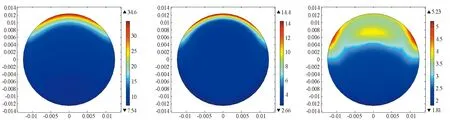
(g) t=1.11×10-9 s (h) t=1.05×10-8 s (i) t=1×10-7 s

(j) t=1.1×10-5 s (k) t=1.05×10-4 s (l) t=0.001 s图6 等离子体与强电磁脉冲相互作用中电子能空间分布的演变过程Fig.6 Time dependence of the spatial distribution of the electron energy in the interactions between HPM and plasma

随着作用时间的增加，电子能峰值继续朝向等离子体上边缘区域移动，两峰值点也逐渐汇合，在等离子体上边缘区域产生单一的峰值点。而后，等离子体中雪崩效应产生，大量的高能电子被消耗用于产生新的粒子，等离子体区域的电子能急速下降，但峰值位置仍在等离子体上边缘区域。最后，等离子体内部非弹性碰撞反应变缓，等离子体内部达到新的平衡，电子数密度峰值开始减小，等离子体区域平均电子能开始变得均匀。

4 结论

电子数密度是表征等离子体物理特性的一项重要因素，当高功率微波入射到等离子体中时，等离子体区域的电子分布特性会产生剧烈变化。本文采用COMSOL软件仿真分析了相互作用中等离子体区域电子分布特性，计算结果表明，等离子体内部激烈的碰撞反应是导致电子分布特性变化的重要原因，在高功率微波作用下，等离子体区域电子数密度在数值上会产生显著的雪崩增长变化，空间分布上电子数密度峰值趋于入射方向移动；电子能随入射激励增加呈增长趋势，随电子数密度的增加而减小。