基于波动理论的地震荷载对岩质边坡稳定性特性研究

马英泰

(青海建筑职业技术学院建筑工程系，青海 西宁 810012)

随着国民经济水平的不断提高及建设规模的增大，与经济建设息息相关的各行各业几乎都涉及到大量的边坡问题，因此正确评价边坡的稳定性，对于确保生产建设的顺利进行及人民财产安全具有重要意义。作为一个自然灾害较为严重的国家，我国的地震呈现区域分布范围广、频率高等特点，这些特性使得地震诱发的边坡失稳成为主要的地震地质灾害类型。虽然目前对于边坡的静力学稳定(如静荷载、开挖等静力问题对边坡的稳定性分析及影响)研究较多并已取得较多成果，在工程应用中也得到了大范围推广，但对边坡地震动力学稳定性的分析研究相对较少，且已有研究大多是针对抗震设防方面的，其稳定性分析方法较为单一、简单，主要以静力学极限平衡法为主。为弥补这方面的缺陷，本文以弹性波动理论为基础，考虑不同地震作用下的动荷载效应，建立地震作用下边坡响应的相关波动方程，从而评价地震动力荷载对边坡稳定性的影响，以期为解决边坡动力问题提供参考[1-4]。

1 波动理论

依据波场分解理论可知：假设地震波从底面垂直向上入射，在边坡的底面和2个侧面的法向和切向临空面可视为分别在边坡的底面和2个侧面设置了不同振动条件的黏性阻尼器和弹簧。正确实现波动输入的方法就是使在边界上施加荷载后的黏性阻尼器、弹簧的应力和位移状态与实际状态相符。

1.1 侧面的波动输入

对于侧边界上任一点P而言，总的应力和位移应为自由波场在P点引起的应力和位移与散射波场在P点引起的应力和位移之和，即

σm=σf+σs

(1)

um=uf+us

(2)

式中:σm，um分别为总的位移和应力；σf，uf分别为自由场中P点引起的位移和应力；σs，us分别为散射场P点引起的位移和应力[5]。假设在P点施加的应力为FP，考虑到散射波的应力应满足黏弹性人工边界条件，并将式(1)、(2)代入，则这时P点的应力边界条件为：

(3)

式中：α为边界系数；G为边界单元块体的土粒比重；R为波传播后的衰减半径；ρ为边界单元块体的土体重度；c为土体的黏聚力。

将式(3)整合后可得：

(4)

设侧边界法线方向为x轴，则在侧边界上P点沿3个方向应施加的应力为：

(5)

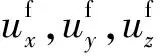
1.2 底边界上的波动输入

同理，在底边界上Q点沿3个方向应施加的应力为：

(6)

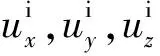
2 动力荷载方程的建立及求解

考虑上述人工黏弹性边界条件以及岩质边坡的自身变形特点，可将岩质边坡视为弹性体。基于弹性力学的相关理论，对地震作用下的边坡动力响应进行理论分析。将含有边坡的山体结构简化为一个等腰三角形，如图1所示，其中山体高度为h，顶部角度为α。

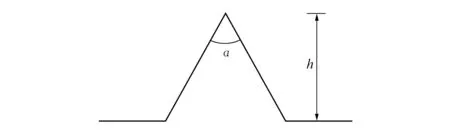
图1 山体边坡简化示意图

考虑上述人工黏弹性边界条件，可将边坡对地震荷载的动力响应问题等效成边坡在边界条件下的弹性力学问题，可将岩质边坡体视为各向同性弹性体，然而由于边坡多为不规则结构，直接求解较为困难，因此需要采用一种新的方法进行分析。

在山体的底部构造一个虚拟的半圆形边界，如图2所示。利用该虚拟边界将山体“一分为二”，根据岩质边坡的构造特性，可将边坡下部及其周边区域定义为A区，将边坡的上体部分定义为B区，其公共边界设为S。为了方便求解，在边坡底部中心和顶点处分别建立两个坐标系，令x轴正方向为水平地表法向向下方向。

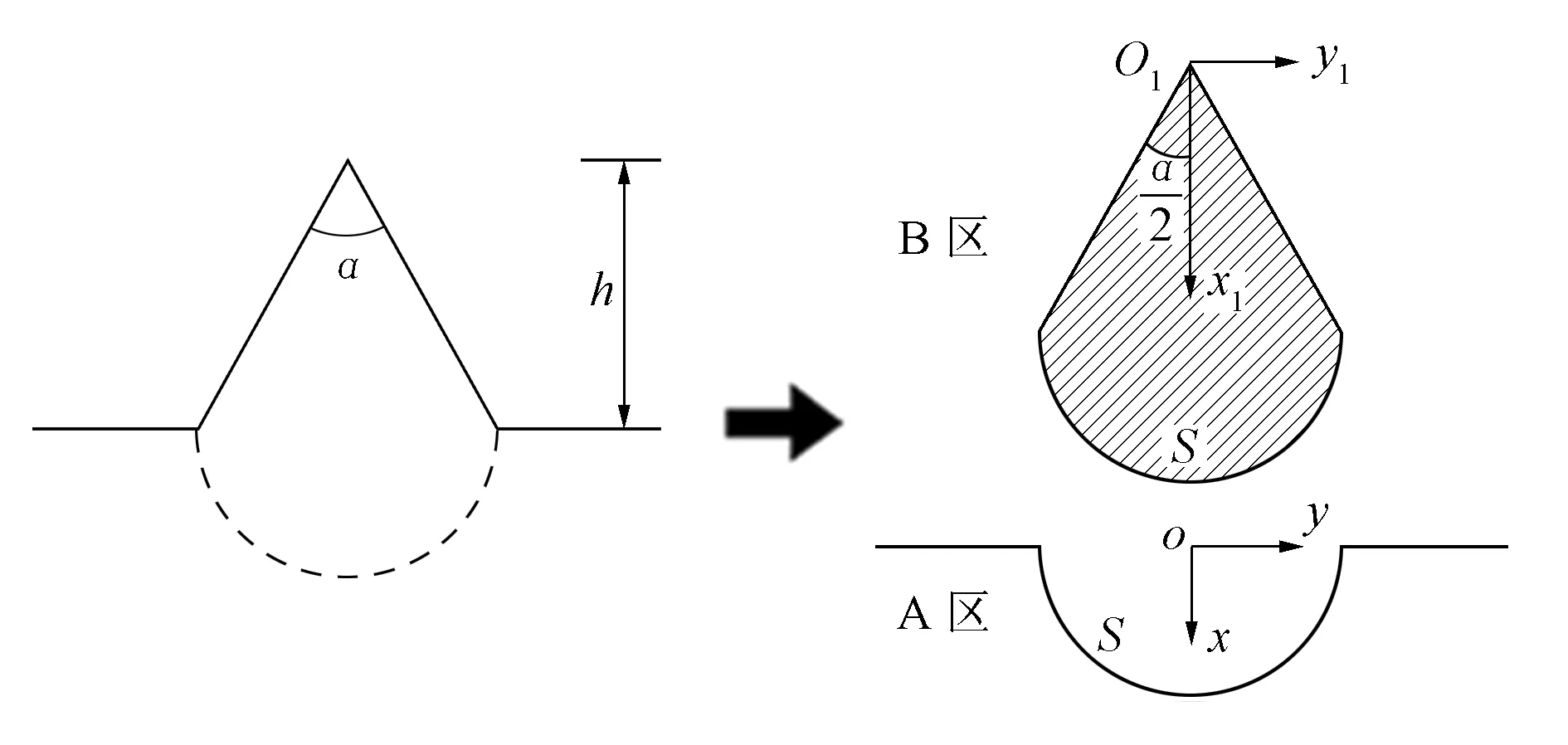
图2 模型分区示意图

以此为基础，利用弹性波动力学相关理论在A区和B区两个区域内分别构造动荷载函数，然后在公共边界S上利用边界条件建立方程组求解，获得在地震动力荷载下岩质边坡的稳定系数。

2.1 动荷载方程的建立

文献[6]中各向同性均匀连续介质地震波的控制方程为

式中：W为土体重度；x为水平向位移；y为竖向位移；cs为介质的剪切波速；t为响应时间。考虑稳态问题，将上述各向同性均匀连续介质地震波的控制方程转化为平面极坐标的形式，可得

(7)

式中：r为极坐标下极向位移；θ为极坐标下角度变化量；k=ω/cs，其中ω为圆频率。

利用分离变量法对式(7)进行求解，求得其通解式为

W=(AJn(kr)+BYn(kr))(Csin(nθ)+Dcos(nθ))

(8)

式中：A,B,C,D为待求常数；Jn(kr)和Yn(kr)分别为n阶的第一类和第二类Bessel函数。

2.1.1A区动荷载方程的建立

由1中地震波底部传播方式可知，地震波入射到A区时振幅可表示为

(9)

式中：W1为波的二次传导后振幅；W0为波函数的最大幅值(后面计算中将其取为1，因此略去)；ε2n为地震波底部传播条件下的应变；J2n(kr)为2n阶的第一类Bessel函数；J2n+1(kr)为(2n+1)阶的第一类Bessel函数β为地震波的入射角。

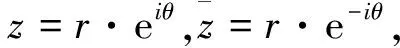
(10)

式中：εm为地震波反射m次后的应变，ε0=1，εm=2(m≥1时)，其中m为反射次数(如m=0则说明不反射，该情况在弹性边界中不存在)；Jm(k|z|)为反射m次后的Bessel函数。

复平面内应力τrz的表达式为

(11)

则入射波、反射波对应的应力τ1为

(12)

其中

(13)

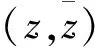
(14)

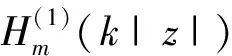
(15)

其中

(16)

式中：τ2为该应力条件下的剪应力。

2.1.2B区动荷载方程的建立

由于B区内存在波的多次反射和叠加，波形复杂，常规方法难以求解，因此需要引入驻波的概念进行进一步计算。假设B区内只存在一种驻波，其产生的效果和多种波反射叠加后的效果等效。B区内的驻波函数应该满足在边坡上应力自由的边界条件，即

(17)

式中：τθz为剪应力。

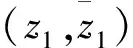
(18)

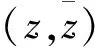
(19)

相应的应力τ3为：

(20)

其中Amγ(z+h)的表达式见式(7)。

2.2 动荷载方程的求解

如此得到了两个区域内波函数的表达式，由于S是一个虚拟的边界，实际上在边界S上应该有位移和应力的连续条件，因此建立方程组

(21)

将构造的波函数表达式代入式(21)，对方程进行傅里叶变换，得到两个无穷代数方程组，求解该方程组，最后得到两组未知系数Am和Bm。

3 边坡稳定性分析

将2中求得的未知系数代入位移和应力表达式中，可得到各区域的位移幅值变化情况。

假设A区半圆形边界的半径为R，入射波的波长为λ，则有入射波的波数η=2R/λ。为研究不同的地震载荷对边坡稳定性的影响特性(即研究不同的波数和入射角与边坡坡面位移幅值之间的关系)，分别以边坡顶角为60°、90°和120°为例，地震波在边坡的左边分别以水平和垂直方式入射，位移幅值变化情况如图3所示。其中y/R=0对应边坡的顶部，y/R=±1对应边坡与水平面的相交位置。

图3为不同的地震波载荷和入射角情况下的边坡响应情况，其中横坐标对应边坡上的不同位置，纵坐标为不同位置对应的位移放大系数。通过分析位移放大系数，可得到地震载荷作用下边坡的稳定性。

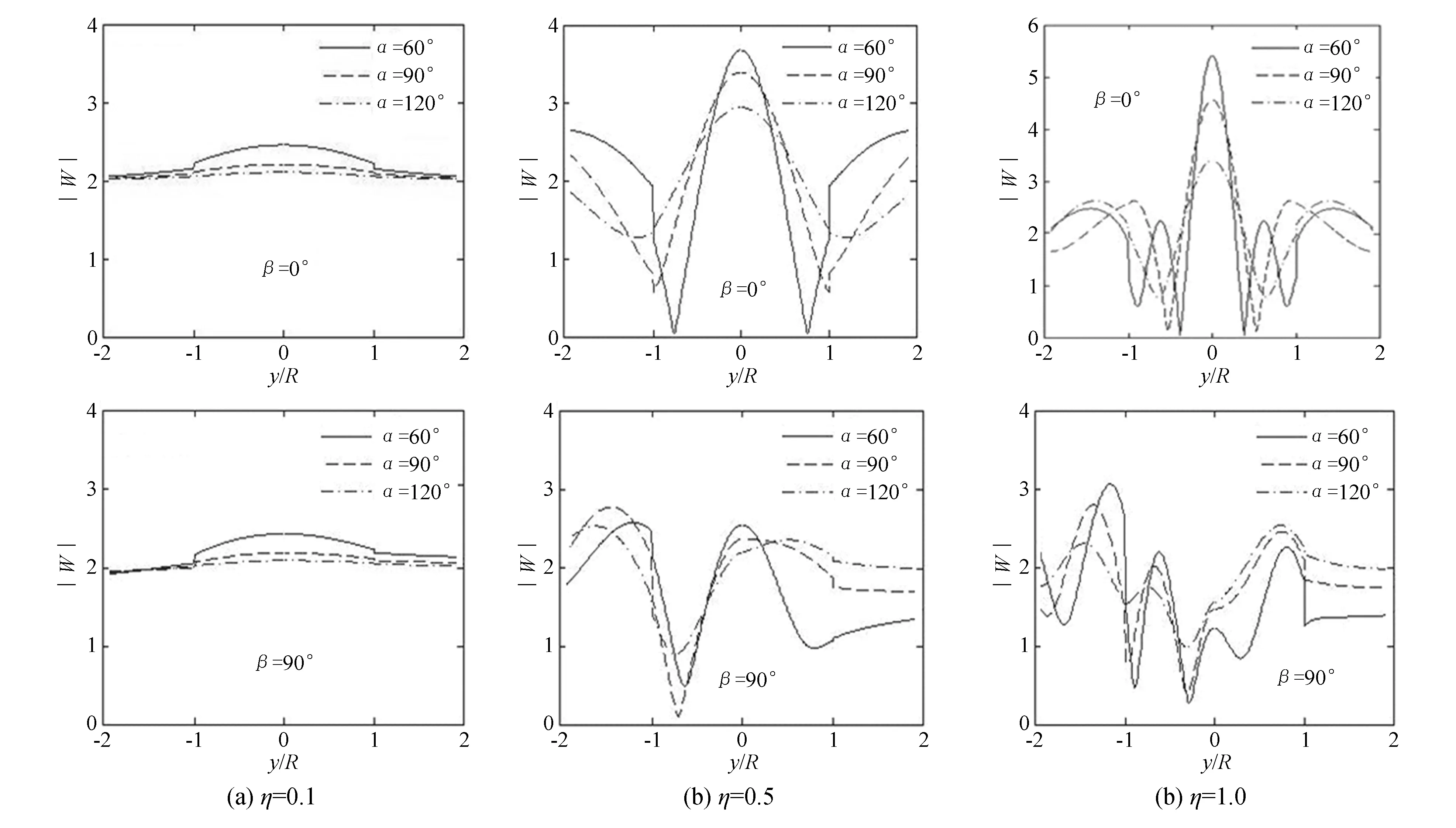
图3 边坡地表位移幅值图

1)如图3(a)所示，当波数较小时，地表位移也相对较小，此时类似于准静态问题，边坡整体位移放大系数约为2.0。

2)随着波数的不断增大，地表位移的变化越来越剧烈。位移放大系数最大值出现在η=1.0时60°边坡的顶点处，约为5.5。

3)地震波垂直入射时，地表位移呈对称分布，其最大值在边坡顶部；地震波水平入射时，地表位移的最大值始终出现在边坡迎向地震波的坡脚处。

4)边坡角度对位移的变化趋势影响不大，但是角度越小，其变化越剧烈。

4 结论

本文以弹性波动理论为基础，考虑不同地震作用下的动荷载效应，建立地震作用下边坡响应的相关动荷载方程，分析了不同的地震荷载对边坡的影响特性，得到以下结论：

1)利用公共边界上的连续条件建立方程组，通过动力学方法求解得到了地震波以不同波数、入射角入射条件下的边坡响应情况，从而进一步评价了地震动力荷载对边坡的稳定性影响。

2)研究结果显示地震波波数、入射角等都会对边坡响应产生不同程度的影响。

3)研究结果可为解决边坡动力问题提供参考依据。

除此之外，边坡形态、坡体材质等因素都会对边坡的响应情况产生不同的影响，以后将进一步进行研究。