海底悬跨管道疲劳寿命计算方法

何张峰，魏 塬，刘树林

(上海大学机电工程与自动化学院，上海 200444)

随着陆地油气资源的日益匮乏，世界各国越来越重视海上油气资源开发，使得大量的海底油气管道被投入使用。由于海床凹凸不平以及海流的冲刷作用，海底管道不可避免地会出现悬跨，在波流联合作用下，极易产生涡激振动(VIV)，从而诱发管道疲劳破坏，因此正确地评估海底管道的疲劳寿命，精确指导、实施海底管道维护措施，对保证管道系统的安全运行具有重要的意义。

金学文[1]通过对海底管道在不同波流组合下的疲劳寿命进行评估，分析了环境因素、悬跨长度对疲劳寿命的影响规律；胡瑾秋等[2]应用断裂力学方法分析了海洋管道焊接接头疲劳失效规律；余建星等[3]运用谱分析理论和疲劳分析理论建立了海底管线疲劳寿命预测方法；高喜峰等[4]运用土体弹簧模拟悬跨管道跨肩处的管土作用，分析了非对称边界条件下的悬跨管道疲劳特性；吕骁翼等[5]提出一套ABAQUS有限元分析方法，将仿真结果与疲劳评估准则相结合计算悬跨管道的疲劳寿命；董文乙[6]基于DNV(Det Norske Veritas)规范，对海底管道疲劳寿命的影响因素(工作内压、海流流速、沟槽深度)进行了分析；Yttervik等[7]研究了海流的流速和方向对海底悬跨段疲劳失效的影响；Sollund等[8]针对悬跨管道疲劳寿命，提出了一种改进的多模态响应预测方法。由上述文献可知，悬跨管道的疲劳寿命与海况密切相关。目前大部分的研究将海流速度假设为定值，仅计算悬跨管道在单一海况下的疲劳寿命。然而真实海况十分复杂，海流速度并不是一成不变的。本文结合真实海况记录数据，根据DNV规范[9]以及疲劳损伤累积理论，以某在役海底管道为例，给出了悬跨管道疲劳寿命的计算方法，可应用于工程中海底管道的疲劳寿命预测以及安全评估。

1 悬跨管道固有频率求解

本文以某海底输气管道为计算实例，该条管道的参数见表1。

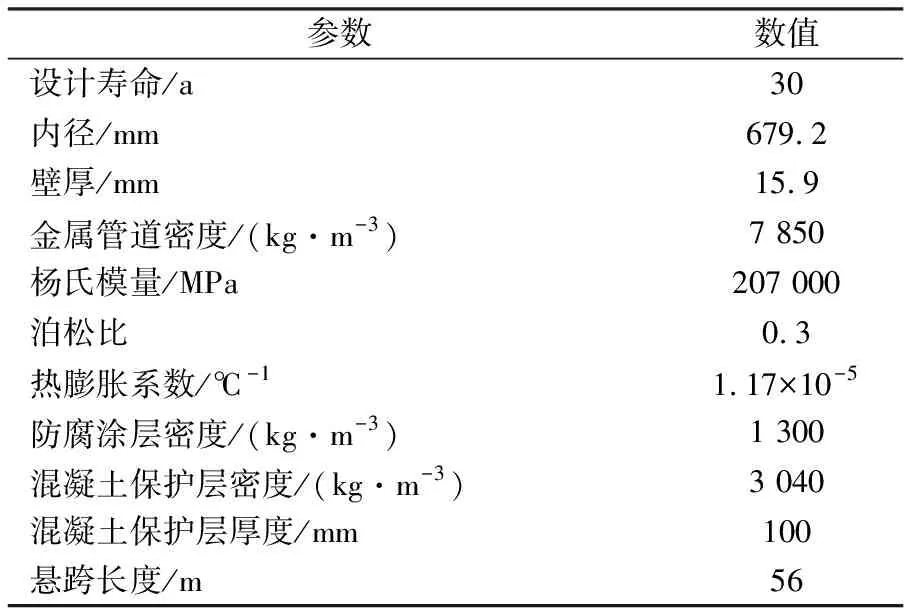
表1 管道参数

悬跨管道的固有频率是计算管道疲劳寿命的重要参数。本文按照DNVGL-RP-F114指导文件，采用土弹簧模拟悬跨段两端跨肩部分的管-土相互作用，在ABAQUS中建立相应的有限元模型，如图1所示。

图1 悬跨管道有限元模型

通过模态分析计算得到悬跨管道前10阶固有频率，见表2。由有限元分析结果可知，第1，3，5，7，9阶固有频率为顺流向，第2，4，6，8，10阶固有频率为横流向。

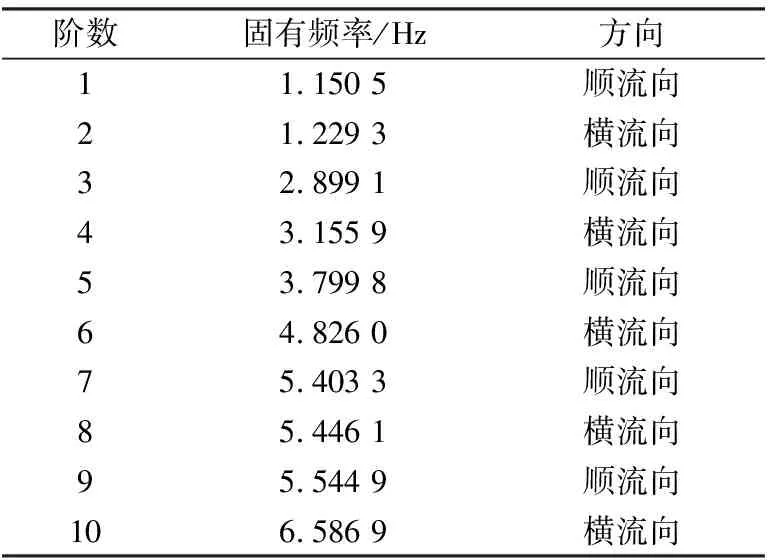
表2 悬跨管道前10阶固有频率

2 海况数据处理

1)波浪数据处理。

原始波浪数据见表3。表3记录了本文算例海底管道所处海域30 a 的海浪海况，每种波浪海况由波浪高度Hs、波峰周期Tp和出现次数f3个参数构成。其中，波浪高度范围为0.7～13.3 m，波峰周期分布范围为2～30 s，经统计，30 a 内的波浪总数为1.8×108，各种波浪海况的发生概率为该波浪海况发生的次数占总次数的比例。

表3 30 a波浪海况参数(部分)

本文采用Pierson-Moskowitz波浪谱法对短期、不规则的波浪海况进行描述。海面谱密度函数Sηη(ω)如式(1) 所示：

(1)

式中：ω=2π/Tw，为波浪角频率，其中Tw为波浪周期；ωp=2π/Tp，为峰值角频率，其中Tp为峰值周期；g为重力加速度；α为广义Phillips常数；σ为谱宽参数；γ为峰值增强系数。

为了进一步得到管道深度附近的波谱函数，需要利用一阶波浪理论，通过频率传递函数G(ω)将海面的谱密度函数Sηη(ω)转化为海底管道附近的谱密度函数SUU(ω)：

SUU(ω)=G(ω)2·Sηη(ω)

(2)

第n阶谱矩Mn可定义为：

(3)

考虑到波浪与管道之间存在夹角，从而引起波浪速度的衰减，可得到在管线附近的有效波浪流速Uw：

(4)

式中：M0为0阶谱矩；RD为缩减系数。

由于波浪数据方向信息难以统计，保守起见，本文假设所有波浪方向均垂直于管道，即忽略由于波浪与管道存在夹角而引起的缩减作用。

2)海流数据处理。

海床表面海流情况十分复杂，为了方便计算，本文采用三参数威布尔分布表示管道附近的海流变化情况，其威布尔参数见表4。

表4 三参数威布尔分布

三参数威布尔概率分布函数FX以及概率密度函数fX可表示为：

(5)

(6)

式中：x为海流速度。

概率密度函数如图2 所示，在不同区间上的积

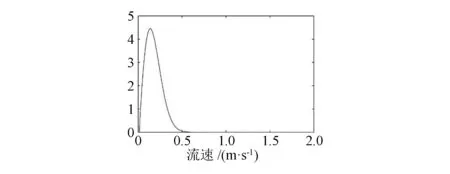
图2 海流速度威布尔分布概率密度函数

分表示海流流速在该区间的概率，将整个区间划分为几个区段，分别求取不同区间的概率，采用区间最大值作为该区间的流速。

流速在区间(a，b)的概率为

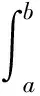
(7)

式中：VR为约化速度；fVR为约化速度VR的概率密度函数。

根据式(7)可求得不同海底稳态海流流速的概率，见表5。

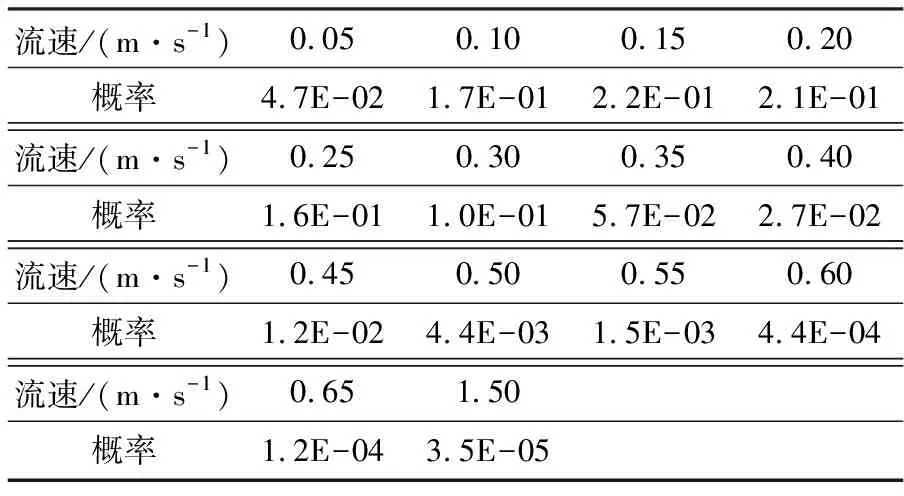
表5 海流速度概率

3 涡激振动响应应力

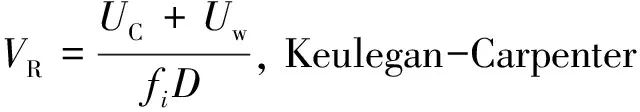
1)顺流向VIV 响应模型。

顺流向响应无量纲振幅与约化速度VR的关系如图3 所示。

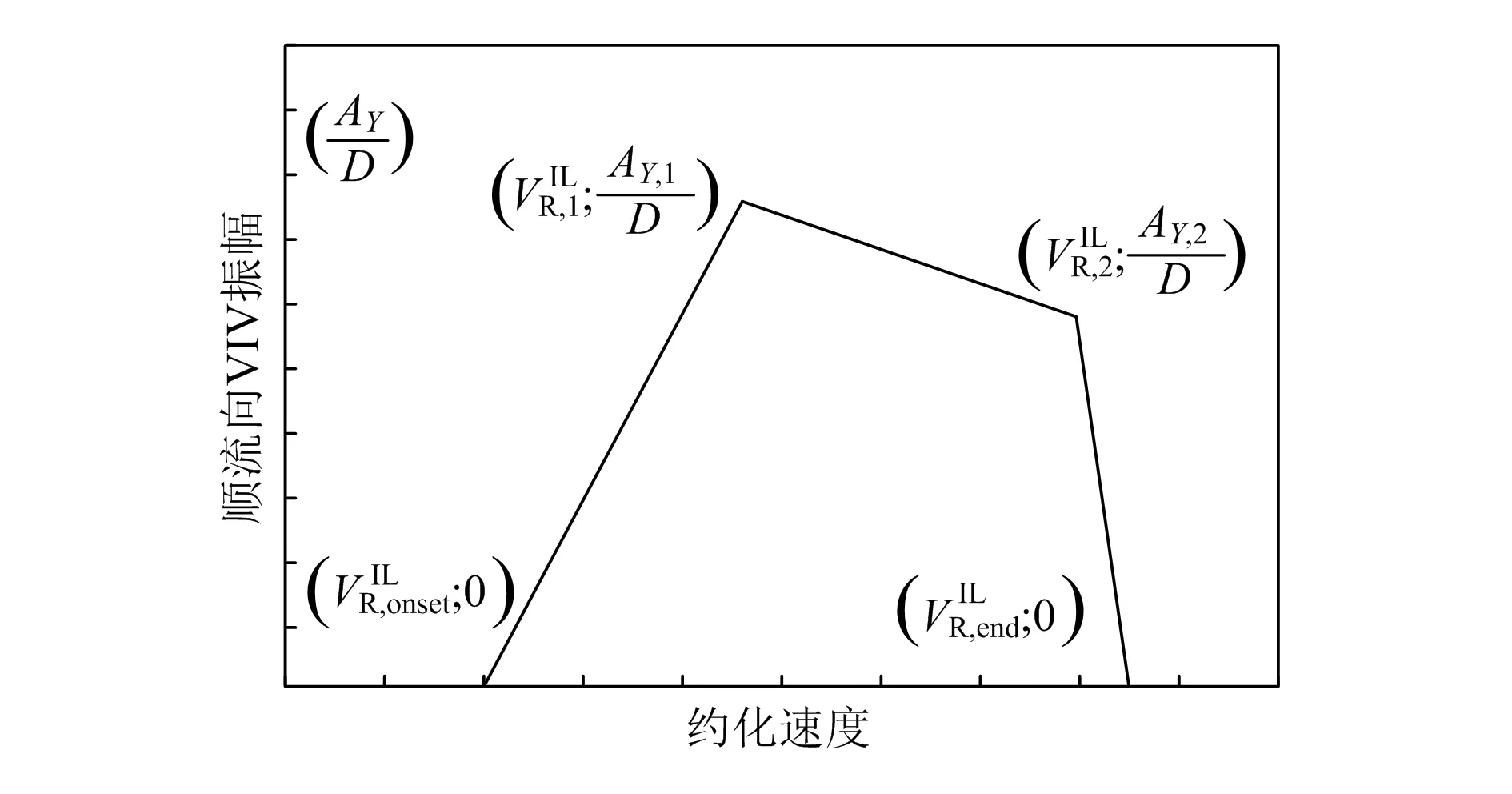
图3 顺流向VIV 响应模型

模型中各坐标点坐标按照式(8)～(13)计算：

(8)

(9)

(10)

(11)

(12)

(13)

式中：γon,IL为顺流向VIV启动速度安全系数；Ksd=Ks/γk，为设计稳定参数，其中γk为稳定参数的安全系数。

(14)

式中：AIL,j为顺流向单位直径应力幅值；ψα,IL为波浪主导海况下海流流速的衰减函数；γS为应力幅值的安全系数。

2)横流向VIV 响应模型。

横流向响应无量纲振幅与约化速度VR的关系如图4 所示。

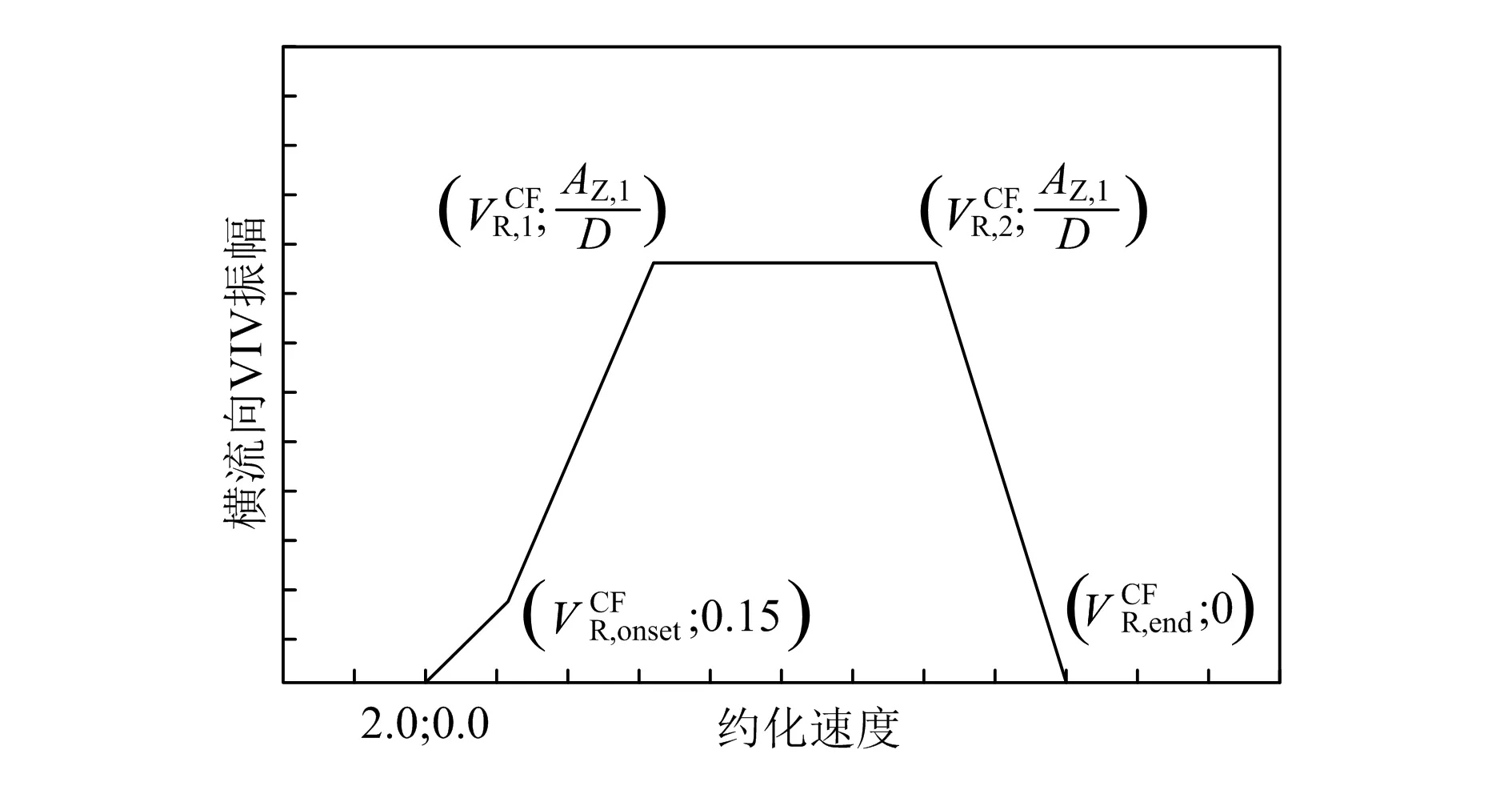
图4 横流向VIV响应模型

模型中各坐标点坐标按照式(15)～(21)计算：

(15)

(16)

(17)

(18)

当α>0.8时：

(19)

当α≤0.8时：

(20)

(21)

式中：ψproxi,onset为考虑海底距离的修正因子；ψtrench,onset为考虑管道与沟槽位置关系的修正因子；γon,CF为横流向VIV启动速度安全系数；fratio为频率比。

横流向响应应力SCF,j为：

(22)

式中：ACF为横流向单位直径应力幅值；RK为考虑阻尼作用的衰减因子。

3)作用力模型。

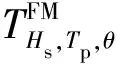
(23)

(24)

(25)

4 悬跨管道疲劳寿命计算

本文采用Palmgren-Miner 累积疲劳损伤理论作为疲劳寿命评估的基本原理，即将各级交变应力引起的疲劳损伤分别计算，然后再线性叠加起来。

(26)

式中：Df为累积疲劳损伤(即总损伤)，且0≤Df≤1；ni为在第i级应力下的循环次数；Ni为在第i级应力下发生破坏的最大循环次数。

将波浪海况以及海流海况一一组合，每一种组合海况对应着一个约化速度，结合相应的水动力参数以及上述VIV响应模型可以计算出悬跨管道在该海况下的响应应力及响应频率，再根据Palmgren-Miner疲劳损伤累积理论，即可得到该海况在整个疲劳周期内造成的疲劳损伤，最后将所有组合海况所造成的疲劳损伤累加，即得到总损伤Df，当Df达到1时表示结构发生破坏。疲劳寿命计算流程如图5 所示。

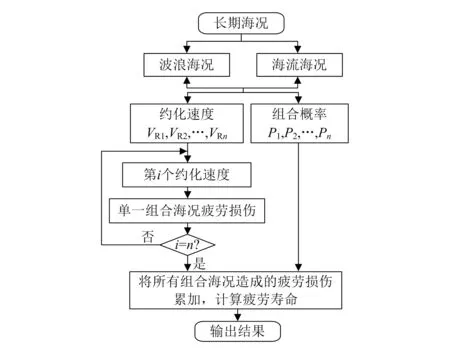
图5 疲劳寿命计算流程

(27)

(28)

综合考虑3 种响应模型，保守起见，选取较小的一个作为悬跨管道的整体疲劳寿命。按照上述计算方法，本文算例悬跨管道疲劳寿命如图6 所示。

由图6 可知，随着悬跨长度的增加，管道的疲劳寿命急剧减小，当悬跨长度增加到75 m 左右时，管道的疲劳寿命已不能满足设计寿命要求，需要及时采取治理措施，防止发生重大安全事故。

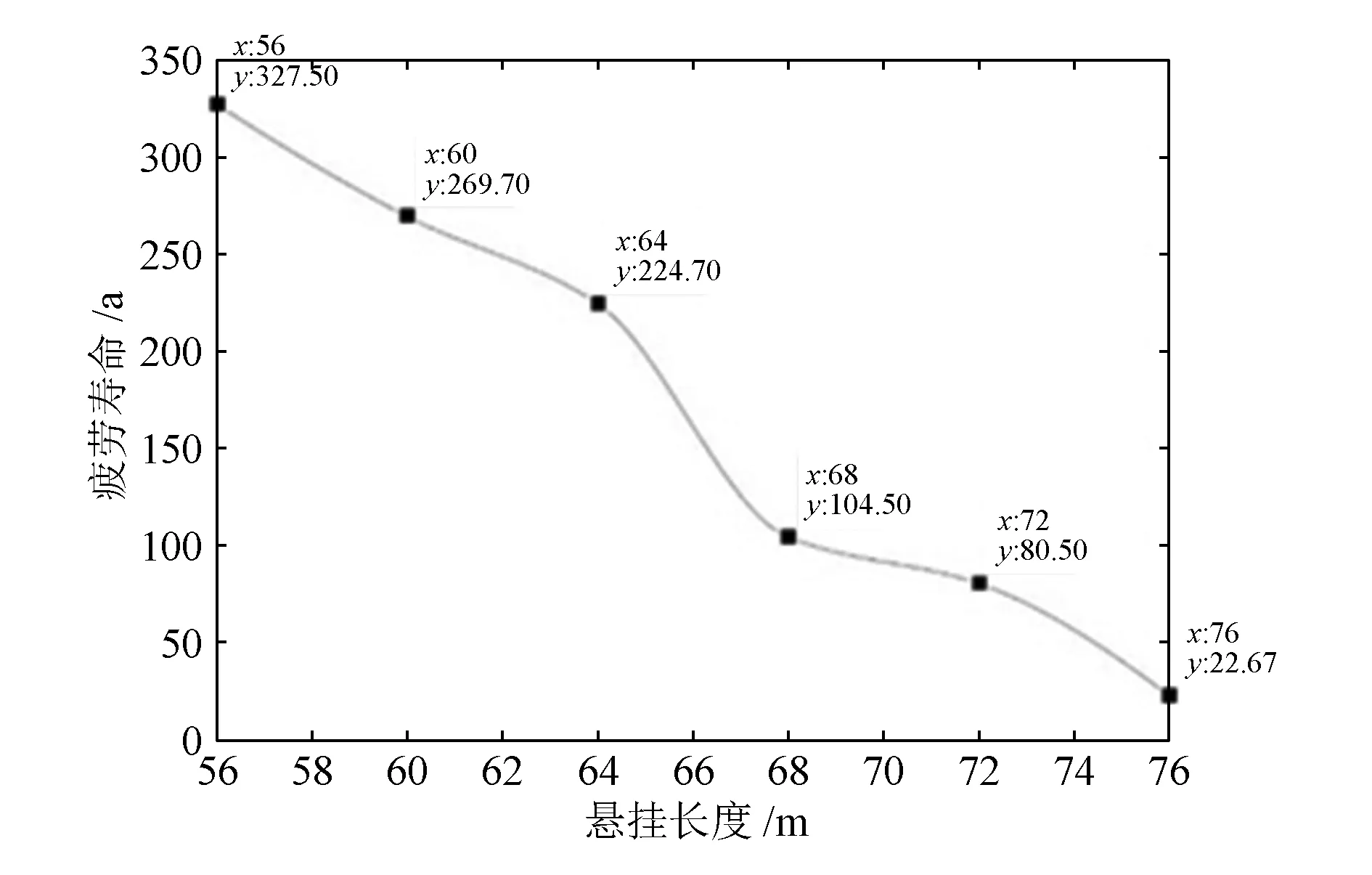
图6 悬跨管道疲劳寿命

5 结束语

本文采用真实海况数据，分别采用Pierson-Moskowitz 波浪谱法和三参数威布尔分布对波浪、海流数据进行处理，结合DNV 指导文件以及Palmgren-Miner 疲劳损伤累积理论，以某海底输气管道为算例，给出了悬跨管道疲劳寿命的计算方法和计算流程。这种方法充分考虑了所有海况对悬跨管道疲劳损伤的贡献，更加符合实际情况，计算结果更加精确，对于实际工程项目中悬跨管道的疲劳寿命预测和安全评估具有较大的借鉴作用。