基于Taguchi方法的ACP100集成式堆顶冷却风管结构优化

胡雪飞，罗 英，王留兵，李 浩，王仲辉，吴冰洁，曹奇锋，张润豪

(中国核动力研究设计院，四川 成都 610041)

在以“华龙一号”“玲龙一号”、AP1000等为代表的先进压水堆型中，常采用一体化/集成式堆顶结构方案。该方案能够同时兼备堆芯探测电缆敷设，控制棒驱动机构(CRDM)定位支承、抗震保护、通风散热等重要功能，还实现了对反应堆压力容器顶盖、顶盖保温层、CRDM、堆顶电缆等设备的集成式吊装，简化了换料工序，节约了换料时间[1]。在“玲龙一号”即ACP100堆型中，集成式堆顶的通风冷却系统为CRDM磁轭线圈散发出的热量提供了冷却流道，如图1所示：冷却空气通过堆顶围筒上部的窗口进入CRDM线圈区域，以风冷的形式带走热量，再从冷却围板上的四个进口进入冷却风管。ACP100的冷却风管采用流线型、对称式布置结构，通过风道四并二、二并一的方式将冷却空气引导至出口。冷却风管的压降和流场分配能力，是其设计合理性的具体指标；同时，冷却风管在整个堆顶结构中的重量、重心，也关系到堆顶的起吊。

图1 ACP100集成式堆顶结构示意图Fig.1 The structure of ACP100 integrated head

传统的堆顶结构通风性能分析多采用试验的手段。而由于一体化/集成式堆顶结构流场复杂、试验成本高昂，更多的研究者们近年来逐渐采用CFD方法进行模拟分析。2013年，于浩等人使用CFX对CAP1000堆型一体化堆顶组件的风冷系统进行了模拟计算，验证了其所选风机的合理性和一体化堆顶设计的科学性[2]。余志伟、何培峰、李燕等人进而耦合温度场，对M310堆顶冷却结构流场和温度场进行了模拟仿真，为冷却结构优化设计提供了科学依据[3]。2016年，何培峰、许斌、罗英等人又对ACP100堆型中集成式堆顶结构可压缩气体与不可压缩气体分别进行了模拟计算，研究了气体可压缩性对对流传热计算结果的影响[4]。

然而，尽管CFD数值模拟方法能够带来极大的便利，在实际中仍然需要花费大量的精力进行试验设计和结构调整。如何简化选型过程、更高效地对堆顶结构进行功能设计与优化，是当前研究中的一个难点。Taguchi方法，又称为田口法，是由日本田口玄一于20世纪发明出的关于质量工程的数理方法。该方法以正交表设计试验，以信噪比作为指标，通过在试验中调整可控因素的水平，来改变噪音对质量特性的影响[5]，进而提高试验方案的抗干扰能力。进一步地，Taguchi方法还可以总结出各因素对质量特性影响的显著性程度，找出各因素的最优水平方案，从而得出质量特性的最优解。

Taguchi方法在试验设计、结构优化、工程质量等领域有着广泛的应用。G.Venkatesan等人利用该方法对波纹板汽水分离器进行了结构优化，筛选出了分离性能最优的波纹板几何结构[6]。张启明等人利用Taguchi方法获得了神州系列某型号5A06铝镁合金过滤器产品电子束焊端面优良焊缝，极大地减少了试验次数，降低了研发成本[7]。史晨阳等人运用Taguchi方法设计试验，优化了曲面底板LED阵列的各项结构参数[8]。王艾萌利用该方法实现了对“U”型转子磁路结构的内置式永磁同步电机的结构参数优化设计，使各性能指标相较优化前有了显著的提升[9]。Taguchi方法在ACP1000一体化堆顶结构的流场优化中有过试算应用，符合工程实践结果，显示出了良好的适用性和科学性。

本文以ACP100集成式堆顶中的冷却风管结构为研究对象，利用Taguchi方法设计试验，使用Fluent 14.5对各试验方案进行数值模拟研究，通过Minitab 17进行后续数理计算，探讨各结构因素和水平对冷却风管性能的影响，求出最优因素水平组合并加以验证，实现对风管结构的优化，提高工作性能。

1 Taguchi方法建模

1.1 物理模型

图2所示的是ACP100集成式堆顶的冷却风管模型图。冷却风管外形结构是以出风管口中心线为轴对称的壳体，分为底层、中层和顶层三层流道。4个进风口跨中均布在同一平面上。冷却空气从进风口沿竖直方向向上进入风管流道，并沿着风管形状流动。风管中的三层流道逐渐合并，冷却空气最终在风管顶部汇聚，从出风口排出。为了便于后续CFD建模，将出风管路合理延长，确保数值模拟过程中流场充分发展。

图2 ACP100冷却风管模型图Fig.2 The integrated head structure of the cooling vent of ACP100

冷却空气通过风管后的压降是衡量其性能的重要指标，在保证通风量满足CRDM线圈散热要求的前提下，尽可能地减少冷却风阻，可以有效地提高堆顶的经济性能。

1.2 Taguchi试验设计

由于冷却风管隶属于集成式堆顶冷却系统，结构优化应在不影响相关外部接口的前提下进行。故冷却风管外形尺寸、进风口尺寸与位置、出风口尺寸与位置应保持不变，不能作为Taguchi方法的可控因素。同时，选择的因素应相互独立，具备非相关性。如图3所示，建立空间坐标轴，选取中层流道中心线角度坐标α，中层流道宽度L，中层流道高度H，出风口接管圆角半径r作为可控因素，各因素及水平的选择见表1。其中，case1冷却风管为ACP100集成式堆顶结构中采用的风管结构。

图3 冷却风管四因素选择示意图Fig.3 Four factors chosen of cooling vent

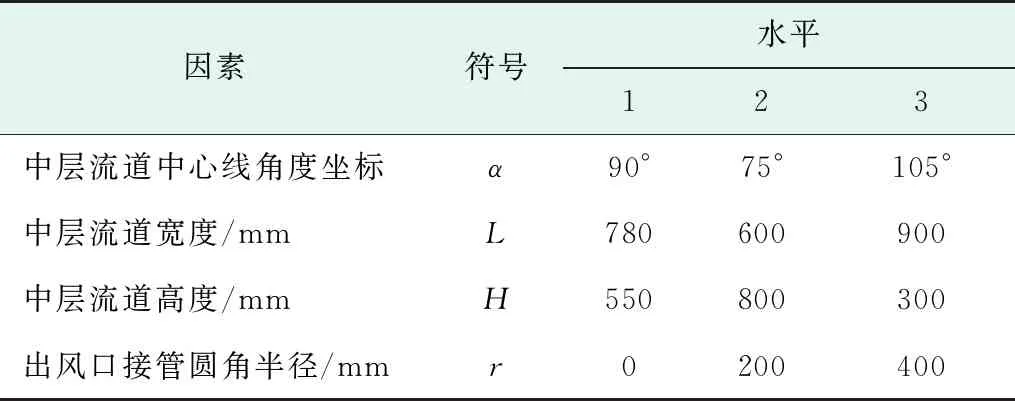
表1 冷却风管因素、水平选择表Table 1 Selection of factors and levels for cooling vent

根据四因素、三水平选择L9(34)正交表，并设计试验方案如表2所示。9种试验风管的三维流道模型如图4所示。

图4 9种试验风管的三维流道模型图Fig.4 3D model for 9 cases of the cooling vent

表2 L9(34)Taguchi方法试验设计方案Table 2 Test design scheme of L9(34) Taguchi method

2 CFD模拟设置

2.1 计算网格模型

使用ANSYS ICEM为图4 9种风管模型进行计算网格划分。按照模型的几何形状，合理划分block区域，采用六面体结构化网格。以案例(1)为例，分别划分出308 616、556 301和716 103数量的网格，结合2.2节中的求解器设置，对计算收敛后进出口的压降采用面积加权平均法进行比较，不同数量的网格压降值及相对误差如表3所示。可知，案例(1)取556 301网格数时已经能够较好地满足精度要求，因此选择该网格作为后续试验中案例(1)风管的网格。其他8种风管结构采用相近的网格划分方法，整体网格数量保证在52～57万，网格雅各比质量均在0.8以上，局部网格结构细节如图5所示。

表3 案例(1)网格独立性检验及模拟精度Table 3 Grid independence test andsimulation precision of case(1)

图5 案例(1)局部网格细节图Fig.5 The details of part grids of case(1)

2.2 求解器设置

使用ANSYS Fluent14.5对冷却风管进行数值模拟。流体选择对应工况温度70 ℃下的空气，认为流体不可压缩。选取能对管内流动、边界层流动等多类型湍流进行高精度求解的Realizablek-ε方程。

在设置边界条件时，模拟实际工况中抽风机的工作方式，将出风口边界条件设置为速度流量出口，速度值为20 m/s，对应实际抽风机41 500 m3/h的风量。设置4个入口为压力入口，压力值为0 Pa。

选取SIMPLE算法进行流体的压力和速度耦合，选择二阶迎风格式作为空间离散格式。在监测各迭代参数残差时，控制残差值≤10-4。

3 结果与讨论

3.1 冷却风管流场特性

通过对9种风管流场进行模拟，可以得到各风管内空气的峰值速度对比，如图6所示。从图6中可以看到，案例(4)风管的峰值速度最高，达到了60.1 m/s。按照式(1)计算当前工况下风管内空气的密度变化情况[10]。

图6 9种风管模型峰值速度对比Fig.6 Peak velocities comparison for 9 cases of the cooling vent

(1)

式中:ρ——峰值速度下空气的密度；

ρs——当前温度工况下空气静止时的密度；

u——峰值速度;

空气比热γ=1.399;

空气常数R=287 m2/s2·K;

工况温度T=(273+70) K。

计算得ρ/ρs=0.987，即空气以峰值速度60.1 m/s运动时，与静止状态下的空气密度相对变化约1.3%，因此在2.2节中认为流体不可压缩的条件设置是合理的。

图7 9种风管模型内部流场速度云图Fig.7 Velocity magnitudes for 9 cases of the cooling vent

图7所示的，是9种风管模型的流场速度云图。冷却空气从同一侧的两个进风口进入底层流道后，向中层流道流动并发生汇聚；在顶层流道与出风口的交点处，来自不同侧的两股流体再次汇聚，向出口管口流出。受总体接口尺寸的影响，中层流道高度减小，底层流道的腔室空间增大。当流体从进风口进入并向上方流动时，会在中层流道交汇区下方形成漩涡，底层流道的腔室空间越大，漩涡的尺度也益发明显，如案例(1)、案例(3)、案例(6)、案例(7)所示。

空气在中层流道汇聚的过程中，随着风管壁面形状的几何弯曲，流体运动方向也发生急速偏转，并在发生偏转且靠近风管壁面区域出现较高的速度，这意味着较大的能量损失。一般情况下，由于进风口2和4在布置方向上更靠近出风管路，从这两个入口进入风管的流体在整个运动过程中的速度方向偏转是最为激烈的；而进风口1和3远离出风管路，从这两个入口进入的空气在偏转过程中，不会出现180°急速变向，运动较为舒缓。因此，在中层流道弯曲近壁面靠近进风口2和4的位置附近常会出现流场的峰值速度。以案例(1)为例，达到了53.8 m/s。

通过改变中层流道几何特性(调整α，L，H)，可以明显变更峰值速度区的出现位置。以案例(4)为例，中层流道中心线位置向出口管路方向偏转15°后，从进风口2和4进入的空气不再出现激烈的偏折，速度梯度变化也相对缓和。而由于底层空间高度的压缩，从进风口1和3进入的空气流道更加狭窄，峰值速度的出现位置改在此侧的中层流道弯曲近壁面附近出现。

在顶层流道与出口接管相贯处增加圆角，也可以明显改善该区域的压降损失。案例(1)、案例(5)和案例(9)均采用了ACP100风管的0圆角结构，从图7中可以发现，由于相贯壁面几何尺寸的尖锐变化，空气在经过尖锐点时会受到较大的扰动，出现高速点，进而在流场后方出现狭长的低速区，使出口管路内的流场迟迟不能发展均匀，这意味着明显的压降损失。而设置圆角过度后，流体圆滑经过管路相交处，后续流场可以很快发展均匀，如案例(2)、案例(4)和案例(6)所示。

通过监测9种风管的进出口静压力，采用面积加权平均法处理，得到9种风管的进出口压降如表4所示。从表中可以看到，9种风管的进出口压降差别显著，其中，案例(5)风管的压降值最高，为1 396.07 Pa；案例(7)风管的压降值最低，为594.58 Pa。案例(1)风管，即当前ACP100堆顶冷却风管结构并不能显示出明显的优势，压降高达1 181.83 Pa。

表4 9种风管方案的进出口压降对比Table 4 Pressure drops comparison for 9cases of the cooling vent

3.2 Taguchi试验结果

为了进一步分析各因素、水平对风管性能的影响，使用Minitab 17软件中的Taguchi方法进行下一步处理。由于压降越低，风管性能越佳，因此本案例属于Taguchi方法中的望小特性，其信噪比公式如式(2)所示：

(2)

式中，S/N——信噪比；

n——试验次数；

yi——输出性能特性

以9种方案的压降作为输出性能特性，代入式(2)进行计算，得到了Taguchi信噪比主效应图，如图8所示。信噪比均值为-59.39，减小中层流道中心角度、减小中层流道宽度、增大中层流道高度都会使信噪比明显降低，即增大风管的压降损失；相反，则可增大信噪比，改善风管内的压降情况。究其原因，这三个因素基本决定了风管内的流道曲折形状，显著影响空气的流程阻力。利用Taguchi方法，通过比较不同因素的信噪比极差，可以得到本试验中各因素对压降的影响程度排秩：出口圆角r>中层流道高度H>中层流道宽度L>中层流道中心线角度坐标α。

图8 Taguchi信噪比主效应图Fig.8 Signal-to-noise ratio in Taguchi

从图8中还可看到，α3L3H1r2为最优的因素水平组合方案。该组合与此前9种方案完全不同。使用Taguchi方法对该组合方案进行预测，信噪比高达-54.19。为了进一步验证该方案的合理性，对α3L3H1r2组合进行建模，并采用同样的数值模拟方法进行试验。优化后的风管三维流道模型如图9所示。

图9 使用Taguchi方法优化后的风管三维流道模型Fig.9 3D model forthe cooling vent by Taguchi optimization

3.3 优化后风管的性能验证

图10是优化后的风管流场速度云图。由于中层流道中心线角度坐标向远离出风口方向偏移，且拓宽了中层流道宽度，从进风口1和3流进的空气不需要经过明显的偏折就可以相继进入中层和顶层流道，减小了流动过程的能量损耗。同时，从进风口2和4处流进的流体在底层和中层流道中有足够的长行程实现偏折，流程变化缓和，故峰值速度低至41.5 m/s。此外，由于中层流道布置位置的变化，流体在顶层流道中的行程也相应增长，截面速度能有足够的行程趋于稳定分布。最后，伴随着出口圆角的设置，两侧的流体在顶层汇聚进入出口管路后，未出现案例(1)中的尖锐速度点与狭长低速区。

图10 经Taguchi方法优化后的风管流场速度云图Fig.10 Velocity magnitude in the cooling vent by Taguchi optimization

将优化后风管的进出口压降同前述的9种方案进行对比，可知优化后的压降低至566.74 Pa，低于9种方案的压降，符合Taguchi方法的预测结果，如图11所示。除了使压降尽可能小之外，优良的冷却风管结构还需要考虑对堆顶围筒内部及CRDM线圈附近的流场均匀分配的功能。使用面积加权平均法统计各方案中四个进风口的截面速度，计算其标准差作为风管对流场分配效果的衡量指标。仍由图11所示，优化后风管四进风口截面气速标准差为0.87，仅稍高于案例(1)(标准差0.41)和案例(2)(标准差0.31)，明显低于案例(3)至案例(9)的对应结果。

图11 各方案风管的压降及速度分配特性Fig.11 Pressure drops and velocity distributions for various cases of the cooling vent

图12所示的，是各方案风管的水平重心与竖直重心坐标位置对比。因各风管结构以X坐标轴为轴对称，故X轴重心即为水平方向重心。由图可知，案例(1)的水平重心坐标为289.9 mm，竖直重心坐标为972.5 mm，受到顶层流道结构产生的力臂影响，整个风管重心处于偏心状态。案例(2)至案例(9)风管受到中层流道结构的影响，水平重心坐标处于214.8 mm至381.2 mm之间。而经Taguchi方法优化后的风管竖直重心坐标为1 018.5 mm，水平重心仅为207.8 mm，水平重心小于全部9种方案。对比案例(1)风管，优化后的风管虽然竖直方向重心增大了4.73%，但偏心量减少了28.3%，这对提高整个堆顶的抗震能力、减小起吊工况下堆顶吊具的偏心载荷有着积极的作用。

图12 各方案风管的重心坐标对比Fig.12 Gravity center comparison for various cases of the cooling vent

因此，经过Taguchi方法优化后的风管结构具有优异的性能，满足优化目的。

4 结论

本文应用Taguchi方法及CFD数值模拟方法，以ACP100集成式堆顶结构冷却风管为研究对象，得到了主要结论如下：

1)验证了Taguchi方法在ACP100集成式堆顶冷却风管结构研究和优化过程中的合理性与可行性。

2)得到了冷却风管结构因素对压降的影响程度排秩为：出口圆角r>中层流道高度H>中层流道宽度L>中层流道中心线角度坐标α。

3)设计出了信噪比最优的风管结构优化方案，并通过CFD数值模拟的方法验证其合理性。最终认为，全新风管结构具备压降低、堆顶流场速度分配均匀度高以及重心偏心量低的优点，可作为ACP100集成式堆顶结构中风管结构优化的较好方案。