基于改进CRITIC-LRA和灰色逼近理想解排序法的空战威胁评估

胡涛， 王栋， 孙曜， 黄震宇， 姜龙亭

(1.空军工程大学 航空工程学院， 陕西 西安 710038；2.95974部队， 河北 沧州 061000)

0 引言

随着新型航空装备的广泛运用，空战呈现出强对抗性、强时效性、高复杂性等特点，准确评估空战环境变得愈加困难[1-2]。面对复杂的空战战场态势环境，对敌方目标威胁进行合理评估，有利于我方飞行员合理决策，采取相应的机动动作，提高生存能力，赢得战场主动权。

目前，用于复杂空战环境下有效区分目标威胁度、实现威胁评估的空战威胁评估方法有很多，研究内容主要是评估指标权重的计算和威胁结果的排序。文献[3-4]等提出将认知理论和直觉模糊推理结合的态势评估方法，能够解决空战信息的不确定性和关联性问题；文献[5]等提出一种将直觉模糊理论和多准则妥协解排序(VIKOR)法相结合的威胁评估方法，能够减少指标权重的模糊性和专家决策的差异性影响；文献[6]提出一种基于直觉模糊集的混合威胁评估方法，能够处理信息的不确定性；文献[7]提出将粗糙集和逼近理想解排序(TOPSIS)法相结合用于威胁评估，减少了专家主观判断对决策的影响；文献[8]建立了基于动态贝叶斯网络的威胁评估推理方法，能够克服专家评价的主观性；文献[9]等提出基于模糊贝叶斯网络的威胁评估算法，能够处理战场不确定信息，但是对先验信息要求很高。

上述威胁评估算法主要存在以下问题：1)指标权重计算依赖于专家的经验知识和主观判断，不同方法的决策差异性过大；2)没有考虑指标体系建立时指标之间的内在关联性，直接运用线性加权理论加权求和得到目标威胁值，忽视了线性加权理论必须满足各指标是线性无关的前提；3)单纯考虑各指标数值信息，不能挖掘评估指标的内部隐藏信息，缺乏对指标序列的综合考虑，从而影响决策结果的可靠性和准确性；4)传统TOPSIS法由于欧氏距离的缺陷，并不能反映各方案的位置关系，导致评估结果不够准确。

确定指标权重一直是空战威胁评估的关键，CRITIC法是通过计算指标之间的对比强度和冲突性来综合衡量指标权重的客观赋权法，具有可信度高、不依赖专家的知识背景的优点；而采用1阶线性回归分析(LRA)可以计算各指标的关联关系[10]，通过削减指标权重降低指标相关性来达到修正指标权重。将二者结合可以更加合理地确定指标权重。同时引入灰色TOPSIS法[11]，将指标间灰色关联度作为距离测度，以更好地反映各方案的内部变化规律，弥补TOPSIS法的不足[12-14]。

1 构建空战威胁评估指标体系

在现代空战对抗环境下进行威胁评估，需要获取敌我双方的能力参数和空战态势信息，而能力参数取决于装备性能。

由系统效用理论可知，指标体系应当具有完备性、独立性和最小性等特点[15]。因此本文建立一个基于空战能力威胁评估和空战态势因素的威胁评估指标体系，如图1所示。

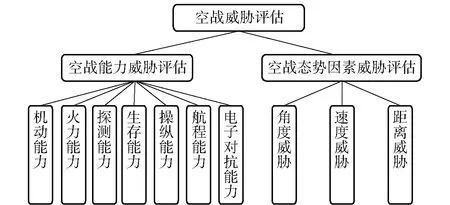
图1 空战威胁评估指标体系Fig.1 Air combat situation assessment index system

1.1 空战能力威胁评估

对于空战中敌机空战能力威胁的评估，不考虑我机在对抗中的影响，根据文献[16]，采用威胁指数法构建单机空战能力威胁模型如下：

(1)

式中：C为战机总体的空战能力；B为战机的机动能力；A1为火力能力；A2为探测能力；ε1为生存能力；ε2为操纵能力；ε3为航程能力；ε4为电子对抗能力。

1.2 空战态势因素威胁评估

在中远距空战中，主要考虑敌我双方的相对角度、飞行速度和相对距离[17]，空战态势几何关系如图2所示。图2中：b为我机，t为敌机；d为我机与敌机之间的距离；vb、vt分别我机和敌机的速度；qb为我机航向与目标线夹角；qt为敌机航向与目标线夹角。

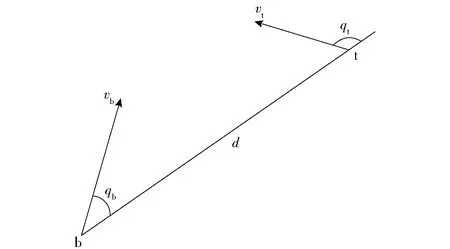
图2 空战态势示意图Fig.2 Schematic diagram of air combat situation

设dmax,b为我机导弹最大攻击距离，dmax，t为敌机导弹最大攻击距离，dr为我机探测设备最大跟踪距离。分别定义角度威胁指数Ta、速度威胁指数Tv、距离威胁指数Td如下：

1)角度威胁指数

(2)

2)速度威胁指数

(3)

3)距离威胁指数

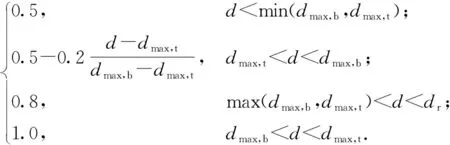
(4)

2 基于改进CRITIC-LRA的指标权重计算

指标权重是空战威胁评估过程中对于空战各态势因素重要性的度量。主观赋权法确定指标权重依赖于专家的个人偏好和知识背景，具有较大的随意性。本文提出一种基于改进CRITIC-LRA的权重计算方法，从空战数据的客观角度出发，充分考虑各评估指标之间的关联程度，并进行指标权重修正，以降低指标关联对威胁区分度和威胁评估结果的影响。

2.1 建立评估矩阵并标准化

假设多属性决策问题有m个评估方案G={g1,g2,…,gi,…,gm}，n个评估指标U={u1,u2,…,uj,…,un}，则m个评估方案对n个评估指标的评估矩阵为Y=(yij)m×n，yij表示评估方案gi中指标uj的值。

由于所选的评估指标类型和量纲各不相同，需要对指标值进行标准化处理，得到标准化评估矩阵X=(xij)m×n.标准化处理方法如下：

1)效益型指标

(5)

2)成本型指标

(6)

3)固定型指标

(7)

式中：δj为固定型指标uj的最优取值。

2.2 基于改进CRITIC法确定指标初始权重

CRITIC法是一种用于在多属性决策问题中确定指标权重的客观赋权法[18]，其基本思想是以评价指标的对比强度和各评价指标之间的冲突性来综合衡量指标的客观权重。对比强度是指同一个评价指标在不同评价方案之间的取值差异性大小；冲突性以各指标之间的相关性来衡量，表征各指标之间相关性大小。

传统的CRITIC法中，设Cj表示指标uj所包含的信息量，

(8)

(9)

式中：wj为指标uj的指标权重。

但是传统CRITIC法的计算公式存在以下两个问题：

1)标准差存在量纲。由于各评价指标的量纲和数量级不同，导致标准差并不能反映评价指标的对比强度。

针对上述问题，本文提出一种改进的CRITIC法，主要是从两方面进行改进：

1)由于传统CRITIC法采用标准差表征冲突强度会带来量纲和数量级不一致的问题，本文引入基尼系数来衡量指标的对比强度。基尼系数是根据劳伦茨曲线定义的，用来表征社会财富在各成员之间的分配差异性，基尼系数越大，表明社会财富在各社会成员之间分配越不均匀[19]，在多属性决策问题中，就是指标对比强度大小的反映。基尼系数的计算公式如下：

(10)

式中：ξj为指标uj的基尼系数，ξj∈[0,1]，1表示该指标的对比强度最大，0表示该指标的对比强度最小。

2)针对皮尔逊相关系数存在的缺点，本文引入肯德尔系数用来计算各评估指标间的冲突性。肯德尔系数是用来衡量多列等级变量相关程度的一种相关系数[20]，取值不依赖于对数据分布的任何假设，适合空战的复杂态势情况。对评估矩阵的任意两列变量Lt和Lj，其中t,j=1,2,…,n，第p个变量分别为Ltp和Ljp.假设Otp和Ojp分别为Ltp和Ljp在Lt和Lp中的排序值，则Otp和Ojp对应排序值变量可以搭配组成变量对集合O.则变量对集合O的第p个变量对为(Otp,Ojp)。因此，指标ut和uj的肯德尔相关系数为

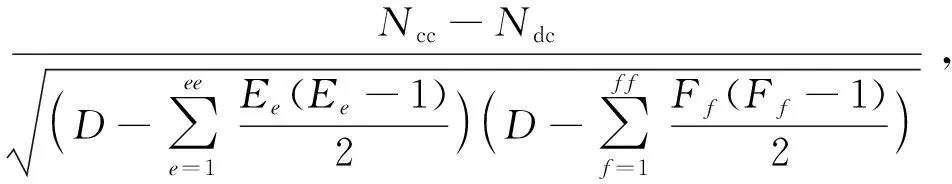
(11)

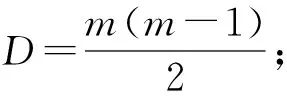
综上所述，可以得到改进CRITIC法的计算公式为

(12)

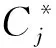
(13)

2.3 基于LRA的指标权重修正

空战威胁评估作为一个多属性决策问题，在决策过程中所选取的评估指标一般存在关联关系[21]，传统思路是严格意义上剔除两两指标之间的关联性，但是需要重新建立评估指标体系。本文采用LRA方法对评价方案集进行分析，得到指标之间的关联性，根据指标间关联关系来修正评估指标的初始权重，以达到减少指标关联性的影响。

2.3.1 指标间关联度矩阵

假设指标ut和uj之间满足线性关系，则可以对指标ut和uj进行1阶LRA. 设Vkj表示指标uj在第k个评价方案中的取值，j表示指标ui对指标uj的1阶线性回归估计值，表示指标uj的平均值，Sa表示总平方和，Sr表示回归平方和，Se表示残差平方和。则关于指标ut和uj之间的关联系数rtj的计算公式如下：

(14)

Sa=Se+Sr，

(15)

(16)

(17)

(18)

最终可以得到一个关于两两指标间的关联性矩阵(rtj)n×n，即

(19)

2.3.2 修正指标权重

rtj的意义为表征指标ut对指标uj有rtj比例的预测。降低指标ut和uj之间关联性的办法就是将指标ut和uj的权重分别乘以(1-rtj/2)，减少的权重部分就是指标ut和uj相关联的部分。

用ut⊗uj来表征剔除指标ut和uj之间的关联性，可得

(20)

用ut⊗U来表征剔除指标ut和属性集U中其余属性之间的关联关系(不包含ut自身)，由此可得

(21)

由此可以得到评估指标的权重修正公式：

(22)

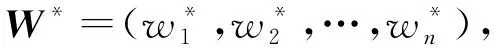
2.4 灰色TOPSIS理论

TOPSIS法是根据有限个评价对象与理想化目标的接近程度来进行排序的一种决策方法，其基本理论是根据计算评价对象与正负理想解之间的距离来进行排序。但是，传统的TOPSIS法存在以下缺点：

1)传统TOPSIS法在计算各待评估方案到正负理想解之间的欧式距离时，如果不能考虑各评估指标之间的线性关系，欧氏距离就会失效，导致评估结果不够准确。

2)传统TOPSIS法由于欧氏距离的缺陷，并不能反映各方案的位置关系，可能存在离正负理想解方案都近的评估方案。

为了克服TOPSIS法的缺点，引入灰色TOPSIS理论。灰色TOPSIS法是将指标间加权灰色关联度作为距离的测度[22]，根据指标数据间整体趋势的相似程度来评价各方案与正负理想解之间的相似度，以更好地反映评估方案之间的内部变化规律，从而克服欧氏距离的缺陷，弥补TOPSIS法的不足。灰色TOPSIS法的步骤如下：

步骤1计算标准化评估矩阵X=(xij)m×n. 由(1)式～(7)式可得到标准化的评估矩阵X=(xij)m×n.

步骤2确定正理想方案X+和负理想方案X-.

(23)

(24)

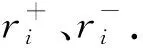
(25)

(26)

式中：ρ为分辨率系数，ρ∈[0,1]，一般取ρ=0.5.

(27)

(28)

步骤4计算每个方案的相对贴近度ηi：

(29)

步骤5根据相对贴近度ηi对敌机进行威胁排序。

3 基于改进CRITIC-LRA和灰色TOPSIS法的空战威胁评估模型

本文建立基于改进CRITIC-LRA和灰色TOPSIS法的空战威胁评估模型。首先根据改进CRITIC法确定指标初始权重；然后利用1阶LRA得到的指标间关联度矩阵，通过削减指标权重对指标权值进行修正，降低指标相关性；最后通过灰色TOPSIS法计算相对贴近度，实现对空战目标的威胁排序。算法步骤如下：

步骤1根据评估方案和评估指标建立评估矩阵，并对评估矩阵进行标准化处理，得到标准化的评估矩阵X=(xij)m×n.

步骤3对标准化评估矩阵的指标序列进行1阶LRA，得到指标间关联度矩阵(rtj)n×n.

步骤4根据指标间关联度矩阵来削减各评估指标权重并进行归一化处理，得到修正后的指标权重W=(w1,w2,…,wn)。

步骤5将修正后的指标权重用于灰色TOPSIS法，得到关于各方案的相对贴近度ηi，按照从大到小的顺序，实现对空战目标的威胁排序。

4 仿真验证

本文采用文献[23]的空战态势数据，假设我机在空战中遭遇敌方6架飞机(F-16C战斗机、F-15E战斗机、F-5战斗机各2架)，我方雷达的最大探测距离为120 km. 我方战机飞行速度为320 m/s，所携带导弹的最大射程为60 km. 空战对抗相对态势如表1所示。

表1 空战态势信息

根据(1)式～(7)式对目标属性矩阵进行标准化处理，得标准化矩阵：

根据(10)式～(13)式，得到评估指标的初始权重为W0=[0.135,0.292,0.352,0.221].

根据(14)式～(18)式可得关联矩阵(rtj)n×n为

将关联矩阵(rtj)n×n形象化展示，如图3所示。

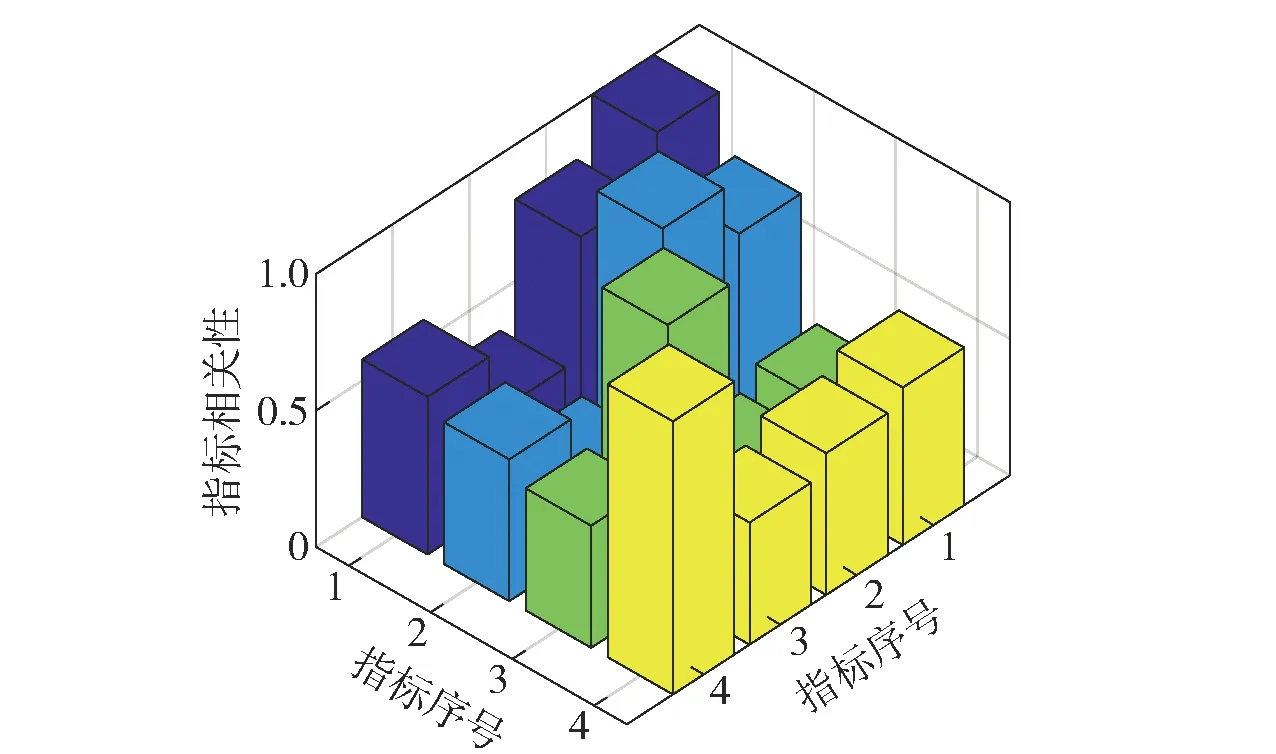
图3 指标间相关性Fig.3 Correlation between indexes

根据(22)式求得修正后的指标权重为

W=[0.107,0.2522,0.436,0.205].

从图3中可以看出，距离指标和其他指标之间的关联度普遍比较小，即与其他指标的信息重合度比较小，所削减的指标权重也比较小，其他指标削减的指标权重大，导致在修正指标权重后距离指标所占权重迅速增大。

可根据(23)式～(29)式确定各敌机与正负理想解之间的加权灰色关联度以及相对贴近度，如表2所示。

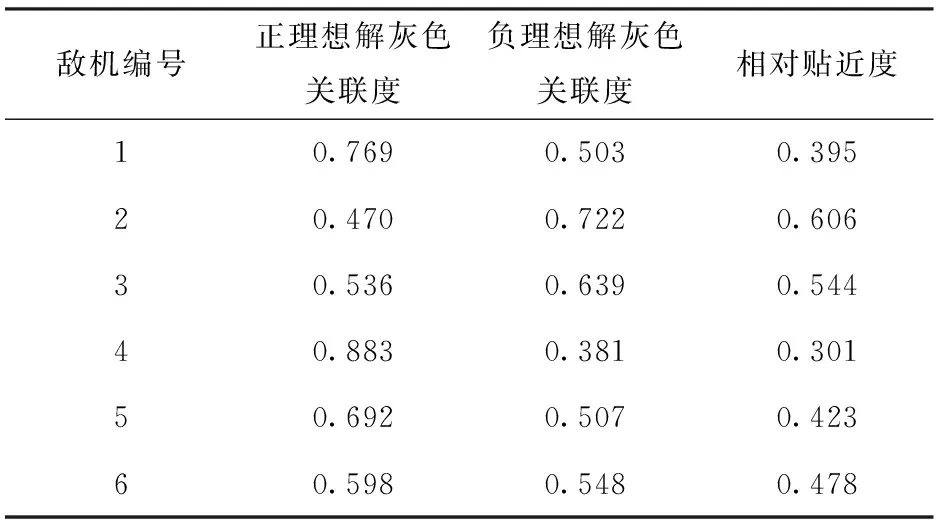
表2 相对贴近度

从表2中可以看出：通过灰色TOPSIS法计算，可以看出敌机2和敌机3与负理想解的距离明显大于与正理想解的距离，威胁最大；敌机1和敌机4与负理想解的距离明显小于与正理想解的距离，威胁最小；根据相对贴近度大小，最终得到敌机威胁排序为2>3>6>5>1>4，评估结果符合实际空战态势。

为了验证本文所提算法(算法5)的有效性，将本文所提改进算法与未改进算法进行对比。

算法1表示基于改进CRITIC和灰色TOPSIS法的空战威胁评估算法，主要用来对比解决指标关联对评估结果产生的影响。相对贴近度计算结果如表3所示。

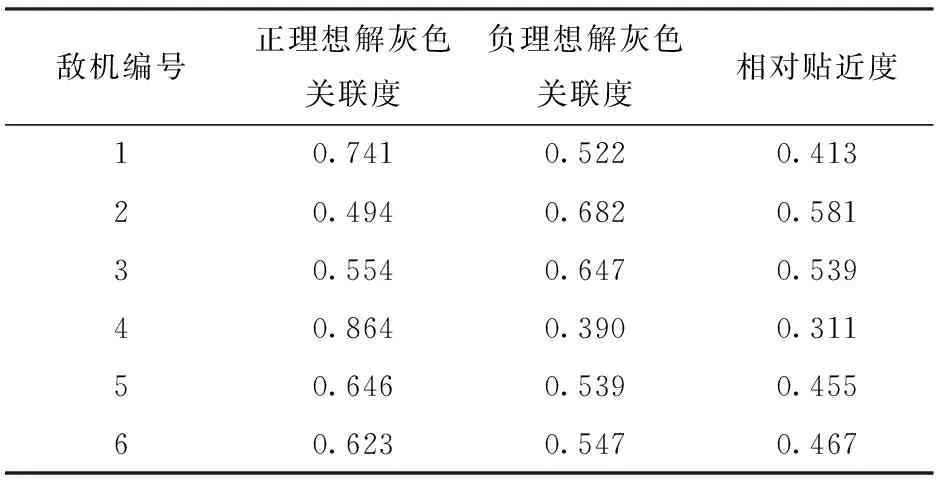
表3 算法1计算相对贴近度

算法2表示基于传统CRITIC-LRA和灰色TOPSIS法的空战威胁评估算法，用来体现改进CRITIC法的优越性。相对贴近度计算结果如表4所示。

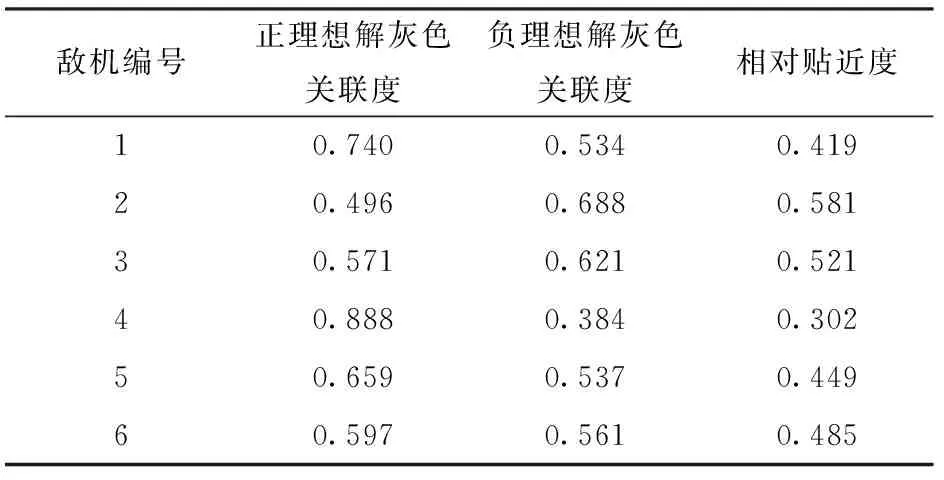
表4 算法2计算相对贴近度

算法3示基于传统CRITIC和灰色TOPSIS法的空战威胁评估算法，主要用来体现改进CRITIC加解决指标关联对评估结果造成的影响。相对贴近度计算结果如表5所示。

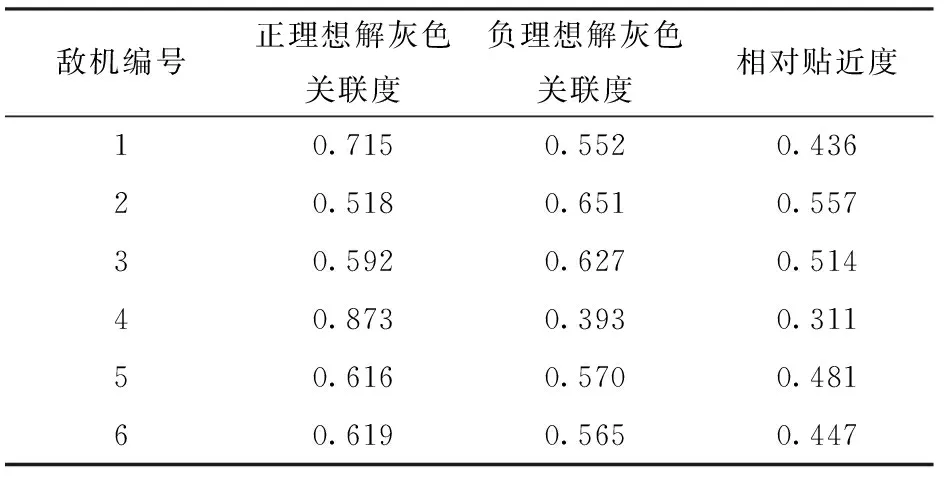
表5 算法3计算相对贴近度

算法4表示基于改进CRITIC-LRA和TOPSIS法的空战威胁评估算法，主要用来体现采用加权灰色关联度代替欧氏距离的优越性。相对贴近度计算结果如表6所示。

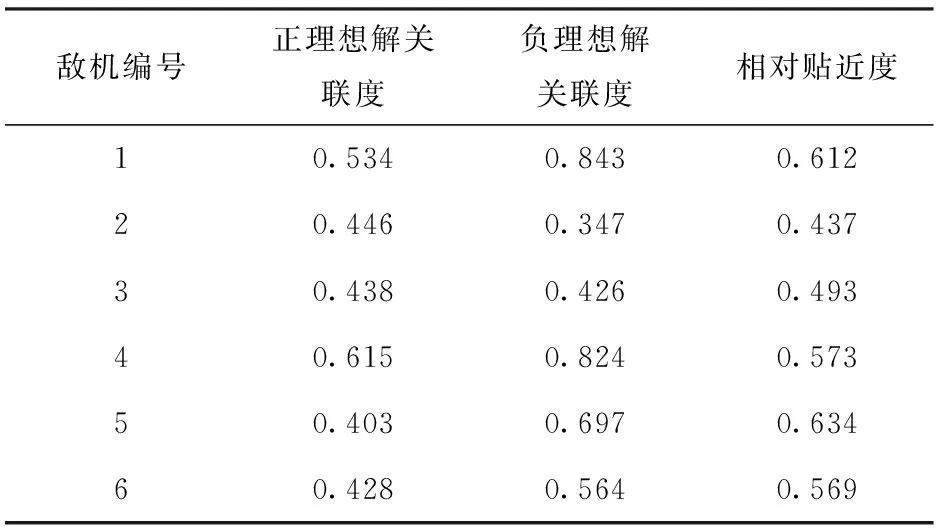
表6 算法4计算相对贴近度

5种算法对比见表7和图4. 从表7和图4中可以看出，本文所提方法和算法1、算法2、算法3在目标威胁排序方面有相似的发展趋势，且威胁评估结果基本相同，反映了本文所提方法的稳定性。

表7 5种算法比较

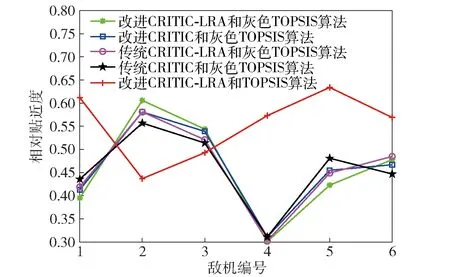
图4 5种算法相对贴近度对比Fig.4 Comparison of calculated relative closenesses of 5 algorithms

本文所提方法和算法1、算法2、算法3对比可以发现，本文所提改进CRITIC计算指标权重、采用1阶LRA来解决指标相关性问题使得威胁区分度比较好，这是因为考虑指标选取时存在的关联关系，从客观逻辑视角来计算指标权重。

本文所提方法和算法4对比可以发现，二者的威胁评估结果存在较大区别，这是因为传统TOPSIS法只考虑指标数据的位置关系，且易受指标间线性关系影响；灰色TOPSIS法不用考虑指标间的线性关系，同时不仅考虑指标数据的位置关系，而且从指标数据的发展变化趋势来解决距离度量问题，所得出的威胁评估结果更加符合战场实际。

为了更好地反映5种算法威胁评估结果对目标威胁区分度的大小，将5种算法所得的相对贴近度按照从小到大的顺序排列，再两两相邻作差，得到顺序相对贴近度差值，结果如表8和图5所示。

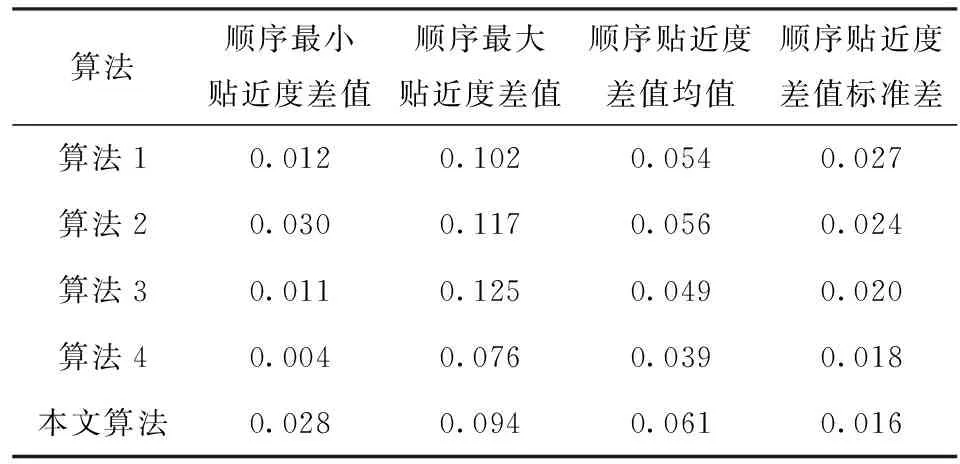
表8 5种算法相对贴近度比较

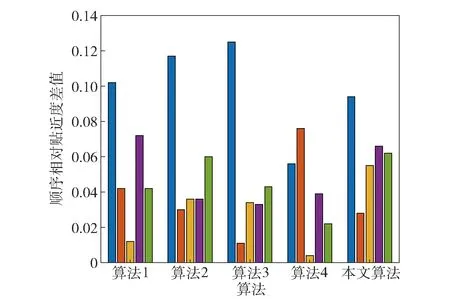
图5 5种算法顺序相对贴近度差值Fig.5 Difference of calculated relative closenesses of 5 algorithms

从表8和图5中可以看出，本文算法在计算相对贴近度时，顺序相对贴近度差值的标准差最小、均值最大，顺序最小贴近度差值和顺序最大贴近度差值都处在次优的水平，这样使得在威胁评估过程中，能够更好地对目标威胁实行区分，威胁区分的可信度更高，威胁排序更加合理。

5 结论

本文针对当前空战威胁评估采用主观赋权法确定指标权重主观性大、评估指标选取存在关联关系导致确定指标权重时存在重复计算，导致评估结果存在误差以及采用TOPSIS法的局限，提出一种基于改进CRITIC-LRA和灰色TOPSIS法的空战威胁评估方法。得出主要结论如下：

1)针对传统CRITIC法存在的不足，引入基尼系数和肯德尔相关系数用来表征指标的对比强度和相关性，使得评估指标权重计算更具有客观性。

2)基于评估指标存在关联关系，导致指标权重存在重复计算的问题，对评估矩阵采用1阶LRA得到指标间关联关系。通过削减指标权重实现对权重的修正，降低了指标关联对威胁评估的影响，也满足了线性加权理论。

3)引入灰色TOPSIS法，将加权灰色关联度作为距离测度，代替欧氏距离，克服了TOPSIS法的局限性，更加合理地对目标进行威胁排序。