二维路面不平度的分形构造方法

张宝振， 王汉平， 张哲， 程梦文

(北京理工大学 宇航学院， 北京 100081)

0 引言

路面不平度是分析路面与车辆耦合作用的基础，而重构准确、可信的路面数字化模型是车辆与路面耦合仿真、车辆动力学性能预测与分析评价的关键[1]。国内外研究路面不平度的模型种类繁多，主要有频域模型、功率谱分析模型、时间序列分析模型等。Liu等[2]基于随机振动理论和随机信号分析提出了一种构建路面不平度的新方法，将路面不平度分解为原始不平度和扰动不平度，然后基于逆快速傅里叶变换(IFFT)方法，借助功率谱密度函数和左右轮辙的相干函数来独立生成原始不平度和左右扰动不平度，最终叠加得到左右轮路面不平度。夏均忠等[3]从平稳和非平稳两方面对各类模型进行了归纳，并指出分形理论在路面不平度激励模型中的应用尚处于起步状态。

Mandelbrot于20世纪创建的分形理论现已广泛应用于分析和处理具有复杂细节特征的自然现象，为人们借助事物内部的自相似性来洞察隐藏于混乱现象中的精细结构提供了新途径[4]。分形理论对描述具有标度率特点的自然现象具有很好的适用性[5-6]，由于路面不平度具有统计自相似性和标度不变性[7]，可用分形理论对路面不平度进行分析。Berry等[8]从纯数学角度研究了Weierstrass-Mandelbrot(W-M)分形函数各参数对该函数性质的影响，并给出基于W-M分形函数的连续形式和离散形式的功率谱密度函数表达式。Majumdar等[9]对比分析了W-M分形函数和传统谐波叠加法在构造粗糙表面时的不同之处，认为W-M分形函数与傅里叶级数的不同之处在于组分中的相位，W-M分形函数的相位因依靠幂级数调节而更具有随机性，但为确保W-M分形函数在定义域内任意点处的相位都具有随机性且不重合，文献[9]中添加了约束条件:轮廓的位置坐标x≠0且分形尺度参数γ=1.5. 文献[10-11]介绍了求分形维数的功率谱法、半方差法、变差法、结构函数法、均方根法、域重新标度法，并对各种方法求解出的分形维数精确度进行了比较分析，认为结构函数法是计算表面轮廓曲线分形维数的有效方法。Chen等[12]分别利用结构函数法、均方根法、变差法、三点弯曲(TPS)法计算分形维数，并从拟合精度、计算精度、计算稳定性3个方面对上述4种方法进行了评价，认为TPS法是最适合且最可靠的提取粗糙表面轮廓分形维数的方法。黄华等[13]提出育苗法来确定无标度区间，进而求得分形维数，认为育苗法求取分形维数的误差较小。袁俊[11]、鲁植雄等[14]和赵兰英[15]基于实测路面不平度数据，利用分形插值函数建立路面不平度的分形插值模型，并将仿真实验与实测路面数据对比，验证了所建模型的可靠性。不足的是，这种方法依赖于道路实测数据，无法对一类路面进行模拟。王若平等[16]提出利用分形维数、路面不平度的幅值系数作为描述路面不平度统计特性的方法，分析了W-M分形函数的功率谱性质，并建立了W-M分形函数的功率谱与路面不平度功率谱的关系，实现了A、C等级路面不平度和实测路面不平度的再现；但未从数学理论角度推导功率谱密度表达式，而是对空间频率进行了平均处理。

综上所述，在利用W-M分形函数模拟路面不平度的文献中，多集中于对分形参数的求解以及求解精度的研究，均令分形尺度参数γ=1.5，而未说明具体原因且未论述γ的取值对选取空间频率的影响，也未明确给出由W-M分形函数推导路面功率谱密度表达式的步骤，同时还未考虑W-M分形函数各组分取值的随机性，只是模拟了单侧路面轮廓曲线。

本文改进了W-M分形函数，使改进后W-M分形函数的各组分取值均具有随机性；以此为基础，从理论上推导出考虑轮辙相干性的左右轮路面不平度的解析表达式，发现了谐波叠加法与基于左右轮相位角相干关系的分形模型在一定条件下的等价性；借助不同轮辙功率谱密度阵的Cholesky分解，得到白噪声滤波的传递函数矩阵，进而利用W-M分形函数构造出更具普遍意义的左右轮路面不平度曲线，并推演出基于相位角相干性构造的分形模型仅是该方法的一个特例。

1 基于组分相位角相干性的二维路面分形构造法

1.1 基于分形理论的路面不平度

Mandelbrot对Weierstrass函数进行推广得到的原始W-M分形函数形式[4]如下：

(1)

式中：Z(x)为路面位移x处的路面不平度；G为路面轮廓的幅值系数，其值与路面等级有关；D为分形维数，表示函数Z(x)在所有尺度上的不规则性，11，n为整数。

W-M分形函数是处处连续、处处不可微分且具有自仿射分形特征的理想曲线，该函数能够对路面等工程表面轮廓进行模拟。在利用W-M分形函数构建路面不平度的文献中，国内外学者均采用的是为适合工程表面而修正的W-M分形函数：

(2)

式中：γn∈[Ωl,Ωu]，Ωl、Ωu为空间频率取值的下限和上限，空间频率的范围取决于研究对象的频率范围；nl=「lnΩl/lnγ⎤；nu=「lnΩu/lnγ⎤。

(2)式表示的路面不平度在x=0 m处不具备随机性，因此考虑在余弦函数中添加随机分布的初相位角θn，改进后的路面不平度表达式为

(3)

式中：θn为均匀分布的随机数，θn∈[0 rad,2π rad]。

1.2 左右轮分形模型组分相位角相干性

由于路面谱是单边功率谱，利用(3)式描述的路面不平度函数Z(x)，可推导出路面功率谱密度函数：

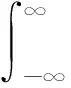
(4)

式中：Ω为空间频率(m-1)；R(τ)为路面不平度函数的自相关函数，τ为位移差；I为虚数单位；L为选取的路面长度；Z(x+τ)为路面位移x+τ处的不平度。

假设左右轮的路面不平度函数分别为Zl(x)、Zr(x)，

(5)

(6)

式中：θln、θrn分别为左、右轮路面不平度函数的初相位角。

相应的自功率谱密度分别为Gll(Ω)、Grr(Ω)，

dxe-2πΩτIdτ=

(7)

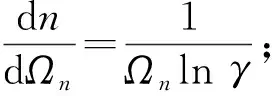
(8)

同理，

(9)

式中：Rrr(τ)为右轮路面不平度函数的自相关函数。

左右轮路面不平度的互功率谱密度函数为

(10)

式中：Rrl(τ)为左、右轮路面不平度函数的互相关函数。

相干函数描述了两个随机过程的频率相关性，且路面不平度是具有零均值的、各态历经的平稳随机过程，则相干函数的平方等于互功率谱模的平方除以两个单侧自功率谱的乘积，即

(11)

式中：γrl(Ω)为相干函数。

文献[17]经过大量试验给出了一种描述不同路面和轮距的路面不平度相干函数：

(12)

式中：ρ为与路面有关的经验值；B为左右轮的轮距。

由此可知左右轮相位角的相干关系为

θln=θrn+sign(α)arccos (coh(Ω))=
θrn+sign(α)arccos (e-ρΩB)，

(13)

式中：α为均匀分布的随机数，α∈[-0.5,0.5]。显然，(13)式与文献[18]推导出的谐波叠加组分相位角的解析相干关系具有一致性。

1.3 左右轮路面不平度

根据国际标准ISO 8608机械振动 路面轮廓 测量数据的报告和中国国家标准GB 7031—86 车辆振动输入 路面平度表示方法，路面不平度的功率谱密度Gz(Ω)可用(14)式表示为

(14)

式中：Ω0为参考空间频率，通常取0.1 m-1；Gz(Ω0)为参考空间频率下的路面不平度系数，对于不同等级的路面，其取值不同；w为频率指数，在路面功率谱密度和空间频率的双对数坐标中表示直线斜率的相反数，通常情况下取值为2.

将推导的自功率谱密度函数与标准路面功率谱密度函数进行对比，故分形维数按照功率谱法进行计算，即

5-2D=w，

(15)

(16)

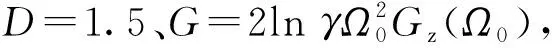
(17)

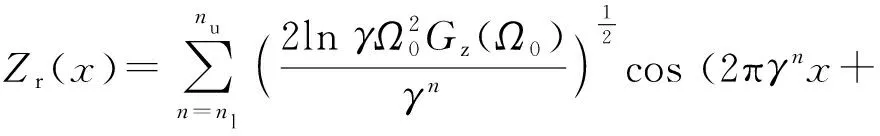
(18)

1.4 路面分形模拟法与谐波叠加法的关系

由于频率Ωn=γn，则ΔΩn=γnlnγΔn，而在W-M方程中Δn=1，故(17)式可写为

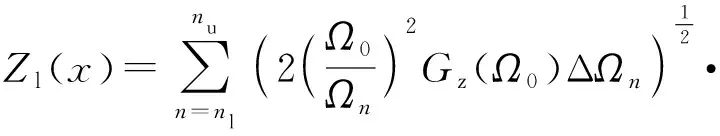
(19)

显然，(19)式在形式上与传统的利用谐波叠加法生成的路面不平度相同。不同之处在于，谐波叠加法中空间频率是按等距选取的，而在W-M分形函数中空间频率是等比例选取的，且比例因子γ>1. 当γ→1时，传统的谐波叠加法与基于相位角相干性构造的分形模拟路面不平度是一致的。

2 基于不同轮辙路面谱阵Cholesky分解的路面分形构造方法

对不同轮辙路面谱阵进行Cholesky分解，得到

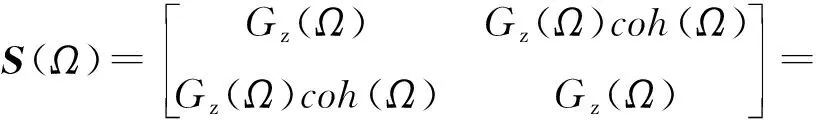
(20)

(21)

式中：S(Ω)为双轮辙路面的功率谱阵；A=cosβ，B=sinβ，C=cos (β+sign(α)arccos (coh(Ωn)))，D=sin (β+sign(α)arccos (coh(Ωn)))，β为均匀分布的随机数，β∈[0 rad,2π rad]。

构造两个相互独立、谱值为1的白噪声w1(x)、w2(x)，其对应的傅里叶变换为W1(Ω)、W2(Ω)，假设不同轮辙的谱阵是两个白噪声经H(Ω)的滤波生成的，则

(22)

依据W-M分形函数，即可构造如下左右轮路面不平度分形模型：

(23)

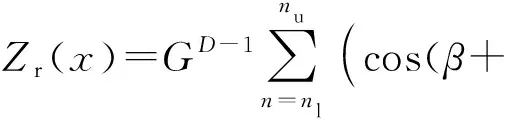
(24)

式中：θn,1、θn,2为初相位角。由(23)式可以看出，当β=0 rad且θn,2=π/2+θn,1时，采用不同轮辙路面谱阵的Cholesky分解构造的分形模拟模型与基于相位角相干性构造的分形模拟模型是完全相同的。由此可知，基于相位角相干性所构造的分形模拟模型只是基于路面谱阵Cholesky分解的分形模拟模型的特例，基于路面谱阵Cholesky分解的分形模拟模型具有更普遍的意义。

3 仿真分析和对比讨论

3.1 路面不平度的仿真模拟

利用MATLAB软件编写二维随机路面不平度生成程序，通过对不同等级的路面进行模拟，得到的模拟路面功率谱密度、左右轮相干性均与对应的参考曲线吻合较好，篇幅所限，不一一列出。本文仅按ρ=1、γ=1.002，对给定空间频率范围0.011～2.83 m-1、长度为2 048 m、宽度为2.5 m的C级标准路面进行模拟。

图1所示为两种方法生成的左右轮辙路面不平度曲线，路面的纵向长度L=2 048 m，轮辙距离B=2.5 m，路面等级为C级，空间频率范围从0.011～2.83 m-1，路面不平度均值为0 m. 其中，模型Ⅰ是指基于不同轮辙相位角相干性的分形模拟模型，模型Ⅱ是指基于不同轮辙功率谱阵Cholesky分解的分形模拟模型。

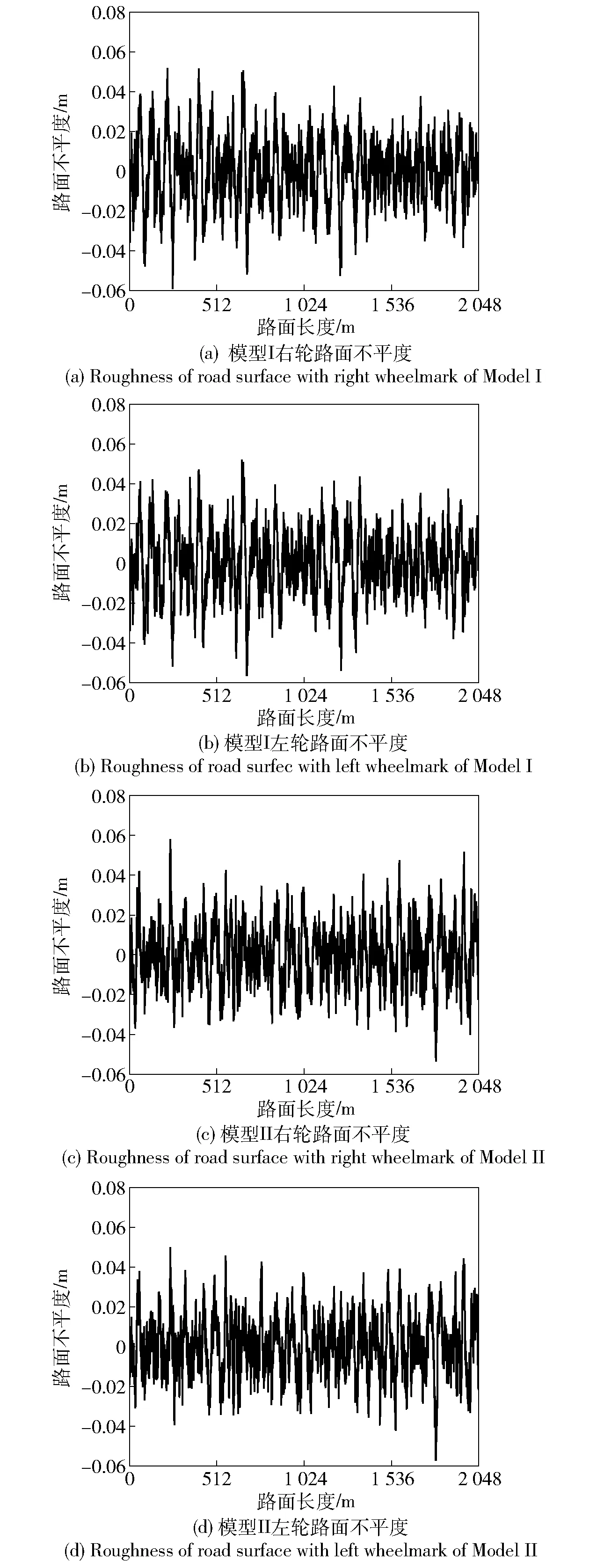
图1 两种分形模型仿真生成的左右轮路面不平度曲线(C级路面，B=2.5 m，ρ=1)Fig.1 Roughness curves of road surfaces with left and right wheelmarks generated by two fractal models(C-grade road，B=2.5 m，ρ=1)

3.2 功率谱及相干函数的对比及分析

图2和图3分别为左右轮轮辙功率谱密度和相干函数的仿真曲线与对应标准参考曲线的对比。从图2和图3中不难看出，两种模型的仿真轮辙自功率谱与标准路面功率谱在较高频区域略有差异，在其余频率范围内拟合效果较好。这是因为W-M分形函数对频率的选取呈幂级数分布，较高频区相邻频率的间隔相对于中、低频区的频率间隔较大，即高频区的频率点分布比较稀疏。图3表明不同轮辙间的相干函数也与参考相干函数符合较好，从而验证了本文推导的左右轮轮辙相位角的相干性关系以及由左右轮轮辙功率谱阵Cholesky分解得到的传递关系是合理可信的。图3中两模型的仿真相干性与指定参考曲线，以及两模型得出的仿真相干性均存在一定差异，其原因在于两模型都是随机模拟，在相干性方面确实容易出现离差，这是随机模拟无法规避的问题。

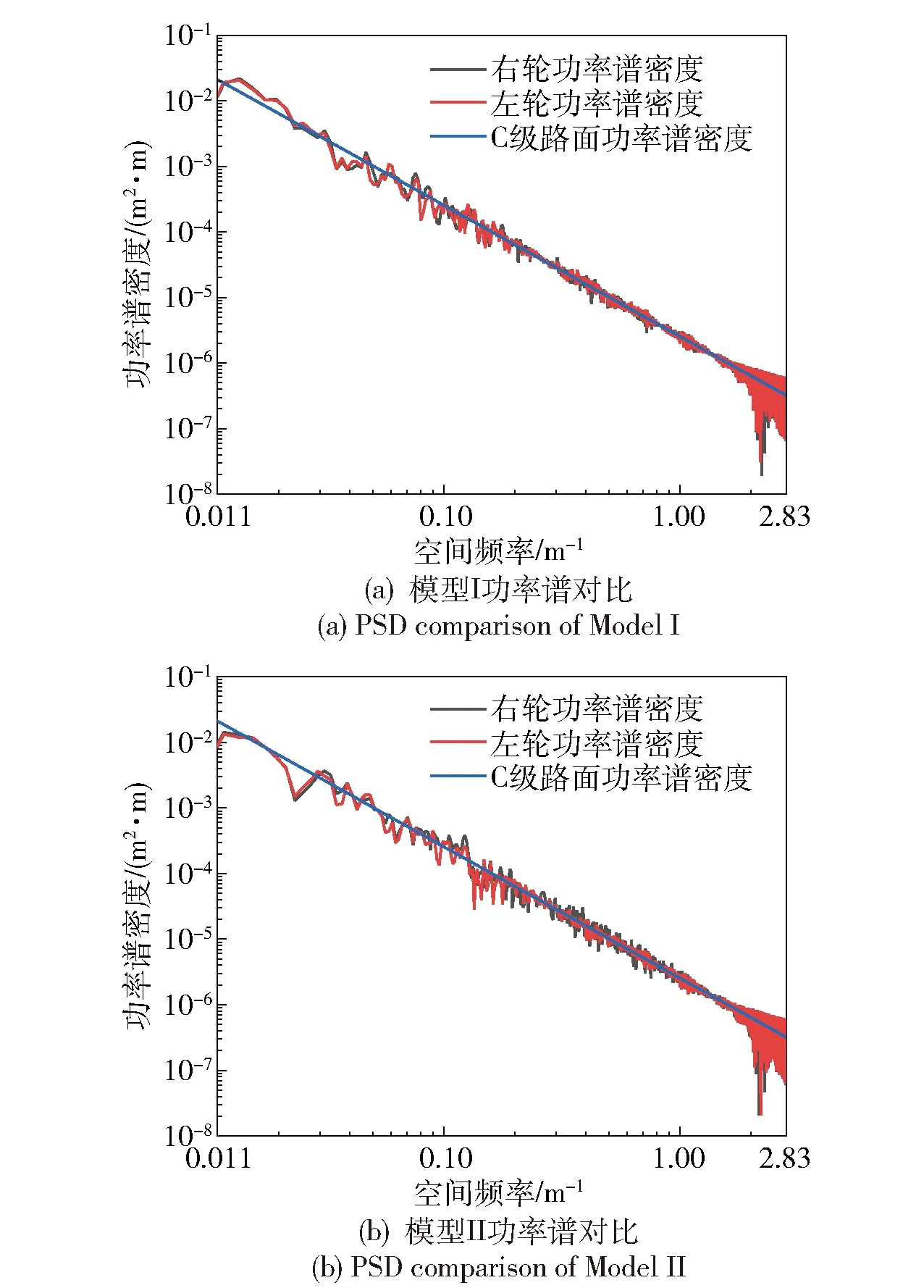
图2 左右轮路面不平度功率谱密度函数对比(C级路面，B=2.5 m，ρ=1)Fig.2 Simulated PSD of road roughness for left and right wheelmarks(C-grade road，B=2.5 m，ρ=1)

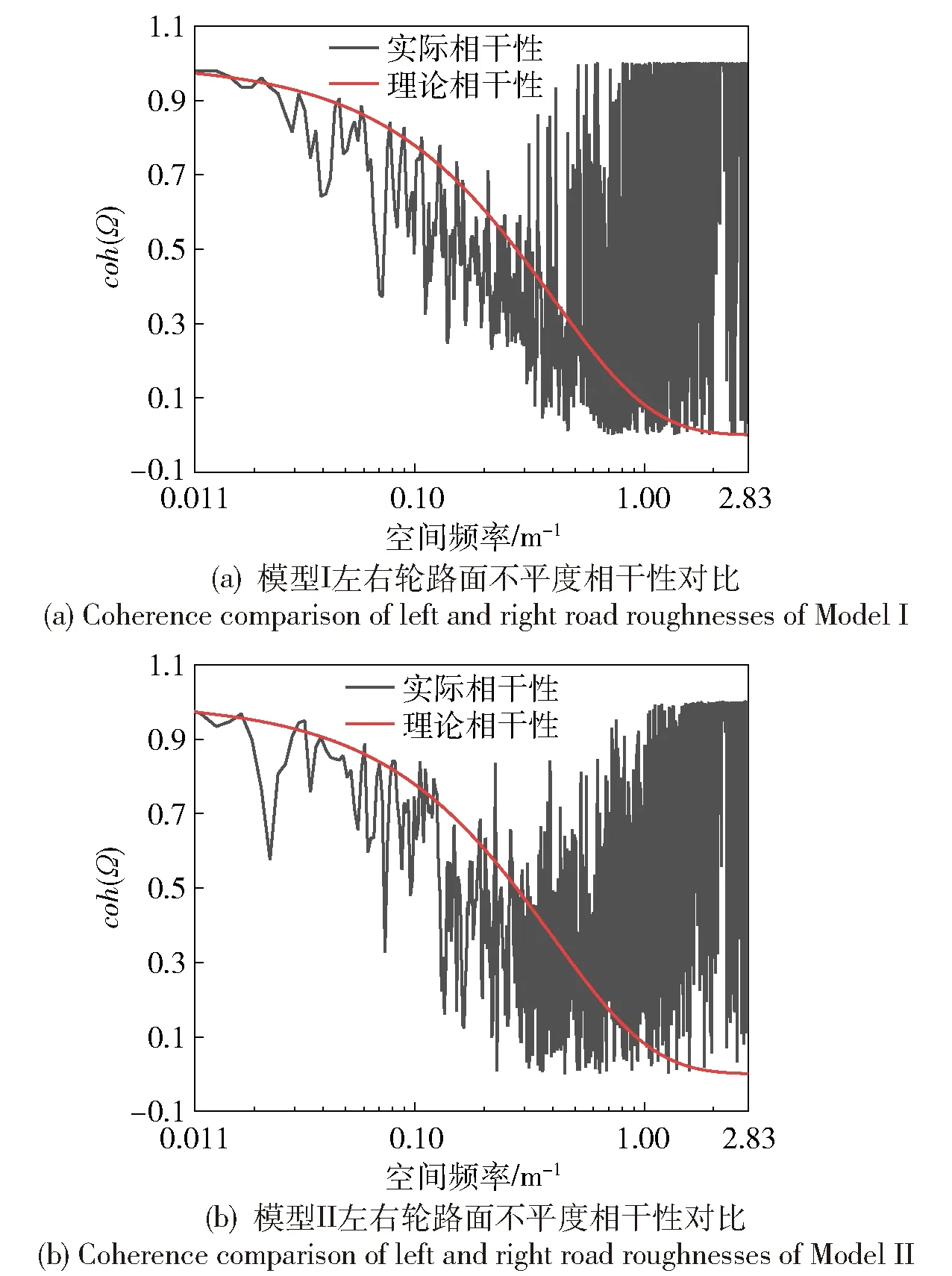
图3 左右轮路面不平度相干性对比(C级路面，B=2.5 m，ρ=1)Fig.3 Coherences of left and right road roughnesses (C-grade road，B=2.5 m，ρ=1)

3.3 γ取值对仿真精度的影响及分析

由于W-M分形函数对频率的选取呈幂级数分布，分形尺度参数γ的取值决定着所选取的频率点数量和频率值，进而影响着拟合精度。下面以模型I为例，研究分形尺度参数γ的取值对路面谱仿真拟合精度的影响。

图4为不同γ取值下模拟功率谱密度函数与标准路面功率谱的对比图。从图4中可以看出：当分形尺度参数γ的取值较大时，左右轮的模拟功率谱密度与标准C级路面功率谱密度有较大的差异；随着分形尺度参数逐渐趋近于1，左右轮功率谱密度拟合效果很好、精度很高。这是因为在有限空间频率范围内，若分形尺度参数γ取值较大，则使得选取的频率点较少，无法很好地拟合标准功率谱密度；分形尺度参数γ取值越接近于1，选取的频率点数量就越多，对标准功率谱函数的拟合效果就越好、精度也越高，但同时计算量也越大。

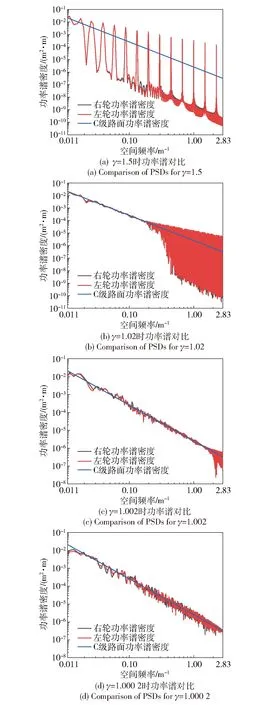
图4 不同γ取值的功率谱对比Fig.4 Comparison of PSDs with different values of γ

4 结论

本文基于W-M分形函数，分别利用相位角相干性和不同轮辙路面谱阵Cholesky分解，推导出左右轮路面不平度分形模型的解析表达式，并得到不同轮辙组分相位角的解析关系。通过对比不同方法推导出的路面不平度解析表达式，得到如下主要结论：

1)当分形尺度参数γ→1时，基于W-M分形函数推导出的路面不平度与传统谐波叠加法所构造的路面不平度是等价的；基于相位角相干性构造的分形模拟模型是基于不同轮辙路面谱阵Cholesky分解构造的分形模拟模型的特例。进一步发现基于路面谱阵Cholesky分解的分形模拟模型具有更一般、更普遍的意义。

2)仿真结果表明：当W-M分形函数中的γ→1时，两模型中左右轮辙的自功率谱密度与标准功率谱密度吻合较好，左右轮辙间的相干性也与参考模型具有较好的一致性，从而验证了基于左右轮相位角相干关系的分形模型和基于功率谱密度阵Cholesky分解的分形模型具有较高的精度和可信性，它们都能很好地用于二维路面不平度的数字模拟。

3)分形尺度参数γ的取值对仿真精度有明显的影响，γ取值越接近于1，路面谱的拟合精度就越高。