水下无人航行器折叠气囊充气展开特性模拟

孙潘， 李斌， 温金鹏， 张晓光

(1.西北工业大学 航空学院， 陕西 西安 710072；2.中国工程物理研究院 总体工程研究所， 四川 绵阳 621900)

0 引言

水下折叠气囊作为常用的水下助浮装置之一，广泛应用于水下航行器的助浮回收、沉船打捞、水下应急救援等领域。对于水下航行器的助浮回收，气囊装置具有产生浮力大、折叠体积小、工作平稳、可重复使用等优点。助浮气囊装置最早由美国、法国、意大利和俄罗斯等应用到水下无人航行器上，如美国MK-54-O轻型鱼雷、法国MU-90轻型反潜鱼雷[1]。折叠气囊在水下及时展开、提供充足的上浮力，是成功带动航行体上浮的一个重要环节。近年来，中国船舶重工集团第705研究所[1]通过对水下气囊系统组成和工作原理进行研究，提出了该装置的一般设计原则及主要技术参数的工程估计方法。随后，705研究所和海军工程大学[2-3]基于经典热力学定理建立了水下气囊充气过程的数学模型，并通过典型试验数据对模拟结果进行了验证。但该方法无法考虑气囊折叠部分的展开过程以及气体与囊布之间的相互作用，是一种半经验、半解析的设计方法，缺少对充气过程细节参数影响规律的认识。使用有限元方法对水下气囊的折叠展开过程仿真分析，可以模拟气囊折叠部分的展开以及囊布与气体之间的相互作用，获得充气过程中气囊的内部状态参数变化，对研究水下气囊的充气展开特性具有重要的意义。

国内外对于气囊折叠展开的研究主要集中在空间充气管以及汽车安全气囊等领域。Salama等[4]和Wang等[5]研究了充气管的展开特性；Lienard等[6]对卷曲折叠管的展开过程进行了模拟；万鑫铭[7]通过实验和仿真研究了多种折叠方式安全气囊对离位乘员损伤影响；马春生等[8]通过对不同折叠方式安全气囊的仿真分析优化设计出一种新型气囊折叠方式；卫剑征等[9]模拟了Z形折叠管的展开过程，并得到了充气速度对展开动力学特性的影响规律。

本文以水下无人航行器所用环形折叠气囊为研究对象，采用初始矩阵法[10-13]建立折叠模型，运用多腔室气囊计算模型模拟气瓶充气方式，结合控制体积法对气囊展开过程进行有限元分析，获得气囊、气瓶展开过程中各状态参数变化。同时研究充气压力、充气管径等参数对展开过程的影响，为气囊、气瓶初始参数的设定提供了参考。在此基础上，考虑气囊展开过程中的环境因素，进一步研究了环境与气囊之间的传热作用对展开过程的影响。

1 充气展开算法原理

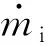
图1 充气过程原理图Fig.1 Inflatable process

本文以单气瓶为例，将气囊和气瓶分离为两个VC[4-5]，假设充气为绝热过程，气囊和气瓶内部压力在同一时刻均等，气囊表面形状随内部压力而改变，气瓶体积保持不变。二者相连处由虚拟隔膜隔开，赋予很小的弹性模量和厚度，避免引入附加约束，隔膜的面积表征着充气孔的面积。流入气囊的气体质量流率与气囊、气瓶的压力、充气孔面积等参数有关[9]，可用一维准静态流管流动方程[15]表示为

(1)

式中：μ、A分别为充气孔有效系数和面积；R为通用气体常数，R=8.314/M，M为充入气体的摩尔质量；γ为气体常数，γ=cp/cv，由充入气体的种类决定，cp为气体的定压比热容，cv为气体的定容比热容；Q为气囊和气瓶的内部压强比，其实际取值与充气时的临界压强比Qc有关，

(2)

Q的实际取值遵循(3)式：

(3)

充气过程为理想气体绝热过程，气瓶内气体状态模型[3]为

(4)

(5)

式中：mg为气瓶内的气体质量。

任意时刻气囊体积可表示为表面积分形式：

(6)

(7)

(8)

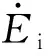
由理想气体能量守恒原理，t+Δt时刻气囊内的气体内能为

(9)

式中：Ea,t为t时刻气囊内部的能量；pa,t为t时刻气囊内部的压强；pa,t+Δt为t+Δt时刻气囊内部压强；ΔV1为Δt时间内的体积增量，ΔV1=Va,t+Δt-Va,t.

根据理想气体状态方程，有

(10)

(1)式～(10)式完成了一次迭代计算，循环逐步递推计算可模拟气囊的动态展开过程。

2 充气展开系统有限元建模分析

2.1 有限元模型的建立

展开系统的有限元模型由折叠环形气囊、气瓶、隔膜、充气管以及水下航行体五部分组成。其中，环形气囊径向截面为圆形，一般采用较为复杂的环向折叠方式[16]安装在航行体上，其本身内外径不等，折叠时无法完全展平，存在大量褶皱。常用的适用于简单三维折叠建模的一般折叠法和适用于可展平型气囊折叠建模的直接折叠法均无法正确模拟其折叠状态，因此，本文采用专门用于不可展平三维气囊折叠建模的初始矩阵法建立水下气囊折叠模型。

初始矩阵法根据气囊实际折叠的形状建立映射网格；根据展开后的形状建立参考网格，二者之间需要保持单元和节点的数目相等，拓扑形式一致。计算中使用*AIRBAG_REFERENCE_GEOMETRY关键字读入表征气囊展开后形状的参考网格。计算开始后，LS-DYNA软件会比较两套网格之间的差异，并据此修正充气过程中气囊的形状变化，在这个过程中，气囊表面没有应力出现。直到气囊的单元恢复为参考网格中的原始形状，囊布单元才开始出现应力，此后可放弃参考构型，采用通常的算法进行计算。这种建模方法能够正确模拟三维折叠气囊、提高仿真效率和精度，但建立参考网格和映射网格之间的映射关系需要花费大量的时间和精力。为得到单元和节点数目相等且拓扑形式完全一致的参考网格和映射网格，考虑到环形气囊的参考网格和映射网格均为规则周期结构，基于安全气囊环向折叠的建模方法[13]编写程序，得到的水下气囊参考网格和映射网格以及折叠截面如图2所示。为保证初始矩阵法的顺利实施，建模过程中忽略气囊上局部刚性排气阀门的影响。本节所建立的气囊展开后体积为40 L、内径200 mm、截面半径100 mm、环向折叠厚度10 mm、折叠高度200 mm.

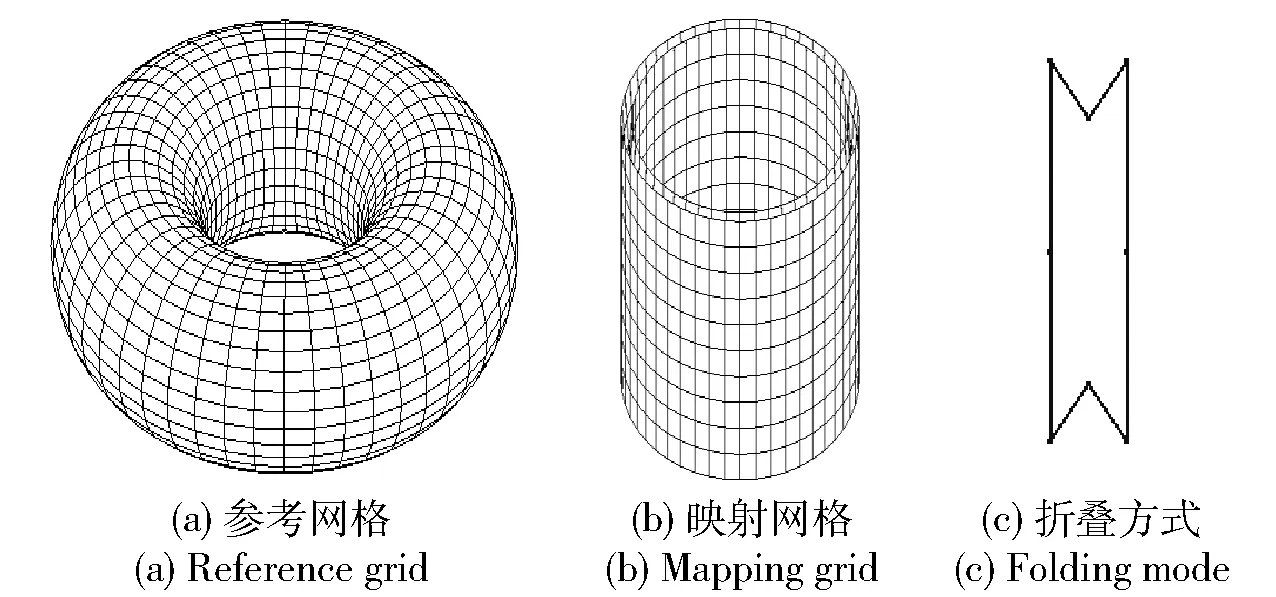
图2 参考网格与映射网格及折叠方式示意图Fig.2 Reference grid，mapping grid and folding mode

2.2 地面气囊展开过程仿真及试验验证

采用2.1节建立的气囊模型，对气囊在地面状态下的充气展开过程从形态变化上进行仿真和试验对比分析。

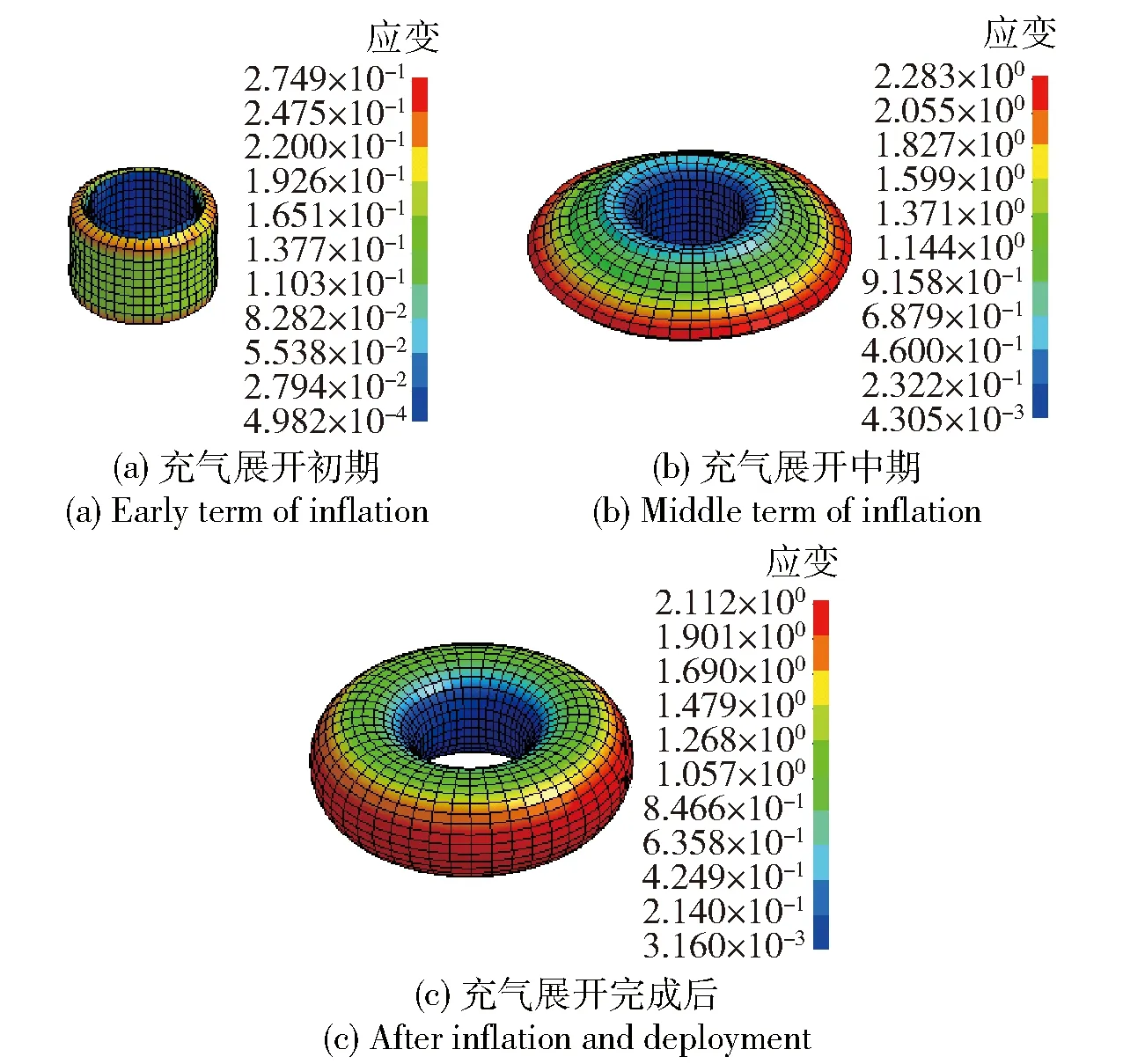
图3 环形气囊展开过程表面应变变化及变形图(0 m仿真)Fig.3 Strain change and deformation diagram of annular airbag during deployment (0 m simulation)

图3所示为仿真过程中气囊表面应变变化及变形图，图4所示为环形气囊在地面展开的过程变形图(地面试验)。对比图3和图4可以发现：仿真分析的环形气囊展开过程变形情况与试验所得基本相符，气囊刚开始展开时内侧受到航行体约束，应变较小，外侧受空气阻力较小，其折叠位置先沿径向展开；继续充气，气囊折叠部分完全打开，外侧应变达到最大，气囊在高度方向继续膨胀，直至完全胀满，最终展开为一个类似于游泳圈的环形气囊。所建立的气囊折叠模型与展开后所得结构与试验所得完全展开后的气囊结构形态一致，验证了本文所建立的气囊折叠结构可以有效地模拟水下航行体所用环形气囊的展开过程，所建立气囊折叠结构的有限元模型是可靠的。

图4 环形气囊展开过程变形图(地面试验)Fig.4 Deformation diagram of annular airbag deployment process (ground test)

2.3 考虑水下压力的气囊展开仿真

以一个40 L的水下助浮气囊为对象，忽略约束盖的影响，用变化环境压强的方式模拟外部静水压力的影响，建立其简化模型开展变参数分析，以总结相关规律，支持水下气囊的设计参数选择。

展开系统的其余各组分在CATIA软件中建立，最后得到的有限元模型如图5所示。图5中，水下航行体储藏气囊的部分简化为一刚性圆筒，体积为3 L的圆柱形刚性气瓶放置其内部。气瓶内部充装气体为氦气。气瓶和气囊之间通过直径为10 mm的充气管连接，在充气管与气囊连通区域建立一个直径为10 mm的虚拟隔膜，以便气囊子系统和气瓶子系统封闭CV的定义。最终所建立的CV模型中，CV1由气瓶与隔膜组成；CV2由折叠气囊、充气管和隔膜组成[15，17-18]。

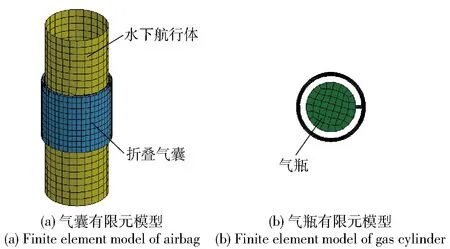
图5 展开系统有限元模型Fig.5 Finite element model of deployment system

建模过程的相关简化及参数设置如下：

1)气囊排气口面积为2 432 mm2，工作压差为50 kPa，LS-DYNA软件中无法设置相对压强与排气口的关系，仿真中将工作压差设置为绝对压强。

2)充气孔有效系数μ=0.5.

4)通过设定不同的环境压强来模拟深水压力的影响，其计算公式为p=pe+ρgh，其中：pe为一个标准大气压；ρ为海水密度，ρ=1 025kg/m3；g为重力加速度，g=9.8 m/s2；h为气囊展开时的海水深度。

基于超星学习通和泛雅网络教学平台的智慧课堂教学模式采用的是“5+5”互动流程，如图1所示。即教师的“备课”“授课”“布置作业”“批改作业”“改进教学”和学生的“预习”“上课”“完成作业”“查看反馈”“改进学习”，这十个环节教学内容相互穿插、师生相互互动，组成完整的渐进式教学模式与过程循环。[2]

5)气瓶和气囊初始条件以及材料参数设置如表1所示。为保持气瓶体积近似恒定，气瓶的弹性模量以及厚度明显高于气囊与隔膜。

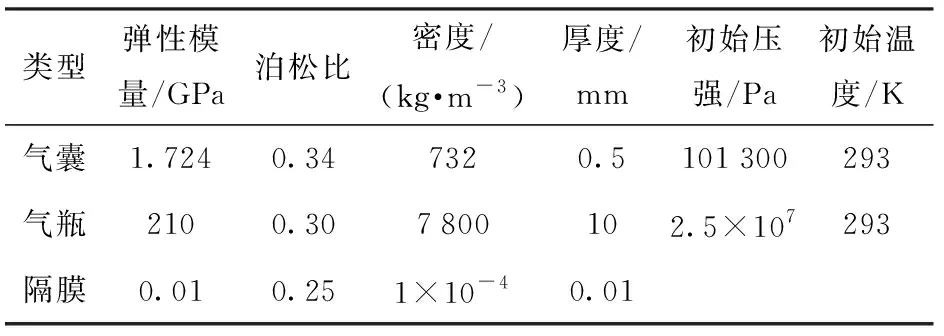
表1 展开系统主要参数

采用2.1节的有限元模型，对气囊在50 m水下的展开过程进行仿真，得到图6所示(只显示环形气囊)气囊充气过程的变形图。由图6可以看出：在计算初期，气囊嵌入式折叠部位分别向上下两侧展开，同时外侧沿径向膨胀，外侧折叠层高度方向变薄，在充气时间为0.034 s时气囊环向折叠部位打开，气囊展开呈圆饼状；随后气囊外侧不再向外膨胀，继续充气使气囊沿竖直方向膨胀，直至0.071 s气囊充气完成，气囊的形状不再发生变化。但此时气瓶内气体并未完全充完，继续充气气囊产生震荡现象。对于充气过程中更多细节的了解，还需要深入分析气囊和气瓶的参数变化曲线。

图6 气囊充气展开过程变形图Fig.6 Airbag deformation during deployment process

为验证仿真结果的可靠性，依据第1节的算法原理，忽略囊布弹性变形，采用解析方法求解气囊水下充气过程并与仿真对比，得到气瓶及气囊参数变化曲线如图7所示。由图7可知，在仿真计算中，气囊开始充气时囊布展开、体积膨胀，此时气囊内外压强平衡；充气至0.063 s时囊布完全展开，体积达到39 L，囊布开始发生弹性变形，囊内压强上升，此后气囊的体积变化是由于囊布弹性变形引起的，气囊的体积变化速率减缓；当充气过程进行到0.071 s时，囊内压强达到工作压力，体积达到40.1 L，排气阀打开排气，保持囊内压强等于工作压力，气囊体积不变；0.478 s，气瓶与囊内压强平衡，气囊的充放气质量流率均降为0 g/s，充气过程完成。与解析解对比，解析求得的囊布完全展开时间为0.064 7 s，达到工作压力时间为0.070 1 s，整个充气过程完成需要0.486 7 s，二者误差在3%以内，表明有限元仿真结果是可靠的。比较解析算法与有限元仿真算法的差别，可知其存在误差的主要原因为解析中未考虑气囊展开过程中的囊布弹性变形，且假定气囊在达到最大膨胀体积40 L之前压强与外界环境压强相等，达到40 L后体积保持不变。而有限元方法考虑了囊布材料的影响以及气囊折叠状态，可全面捕捉气囊展开过程的细节，得到展开过程中气囊的变形历程以及各部分作用力。由此可见相对于解析方法，有限元方法具有更大的优势。

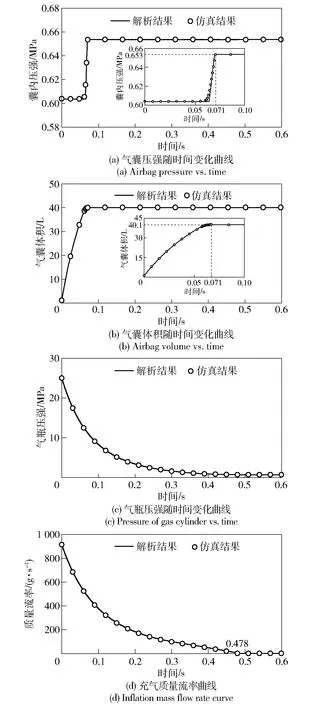
图7 展开系统参数变化对比图Fig.7 Parameter change of deployment system

3 展开系统参数对充气展开过程的影响分析

3.1 充气压力对展开过程的影响分析

气瓶初始压力对展开系统的充气速率有显著影响。基于第2节建立的有限元模型，在10～35 MPa充气压力范围内对气囊在50 m水下的展开过程进行仿真分析，得到的仿真结果如图8所示。

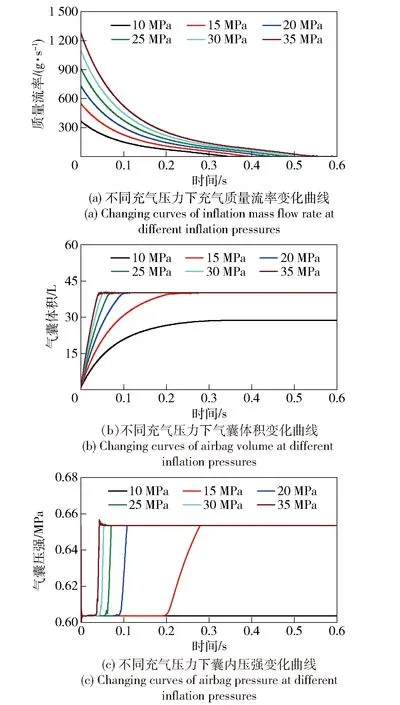
图8 不同充气压力下气囊充气仿真结果Fig.8 Simulated results of airbag inflation at different inflation pressures

从图8(a)中可以看出，同一时刻气瓶初始压力越大，展开系统充气质量流率越高，且经过对比10～35 MPa范围内不同充气压力展开系统的质量流率曲线可知，在气囊与气瓶的压强比小于临界压强比时，同一时刻充气质量流率随充气压力线性增大。同时，由于大充气压力条件下充气速率较快，气囊展开速度加快，展开系统的阻尼也就更大，将更多的动能转化为内能，气囊也更快完成膨胀，囊内压强达到工作压差所需时间更短。在15～35 MPa范围内随着充气压力的增加，展开系统的充气质量流率也随之增加，相应的充气过程所需要的时间越短。图9给出了15～35 MPa范围内充气压力对气囊完全展开时间的影响规律。由图9可以看出，气囊完全展开时间随着充气压力的升高而减小，且其减小的幅值也随着充气压力的升高而减小。但该规律仅适用于气瓶中气体的质量能满足气囊完全展开的需求，对于10 MPa气瓶内气体总量无法完成气囊展开需求的情况，该规律不再适用。

图9 充气压力对气囊展开时间的影响规律Fig.9 Influence of inflation pressure on deployment time of airbag

最大充气深度是指气瓶可以把气囊充满并达到工作压力的极限工作深度，超出该深度后，气囊存在无法上浮的可能。不同充气压力瓶内气体质量不同，气囊可达到的最大充气深度也不同。对10～35 MPa范围内的充气压力，在不同深度条件下仿真分析，得到6种充气压力的极限工作深度，图10给出了充气压力对气囊极限工作深度的影响规律。由图10可见，在10～35 MPa范围内，气囊极限工作深度随着充气压力的增加而线性增加。经过拟合可知，其增长的幅度为充气压力每增加5 MPa，气囊的极限工作深度大约可增加21.5 m. 实际应用中，水下气囊需要在不同的深度回收航行体，此结论可为展开系统气瓶初始压力的确定以及后续上浮过程的研究提供重要的参考。

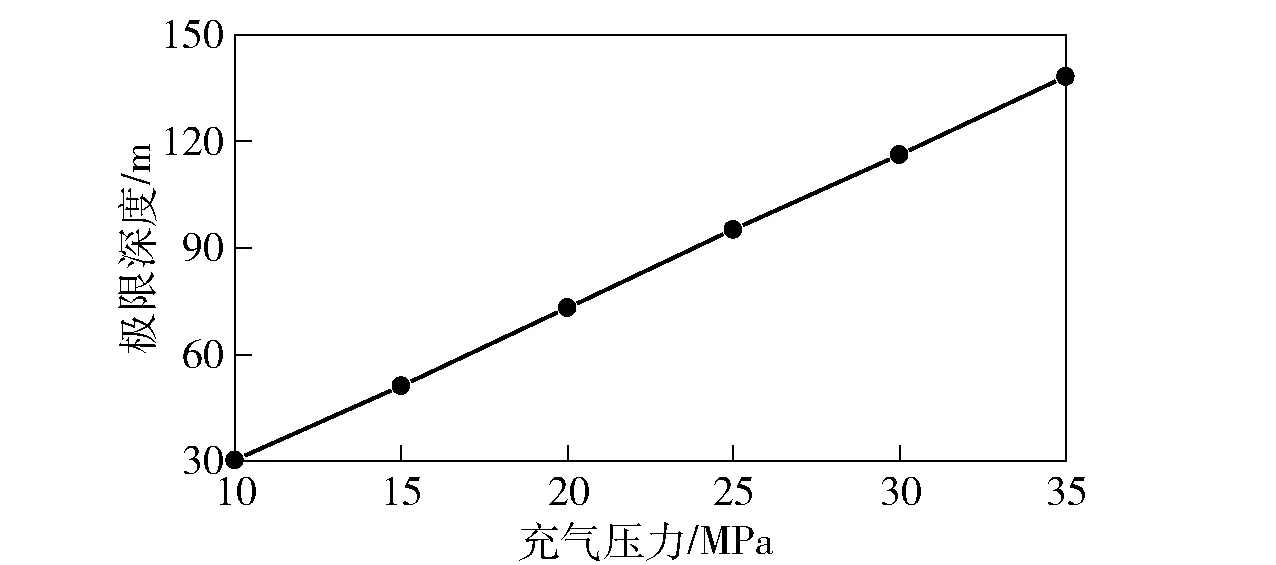
图10 充气压力对气囊极限工作深度的影响规律Fig.10 Influence of inflation pressure on the limit working depth of airbag

3.2 充气管径对展开过程的影响分析

图11(a)为不同充气管径下气囊充气质量流率变化情况。比较图11(a)中4～10 mm范围内4种管径下的计算结果可发现，4 mm管径的初始充气质量流率仅为146 g/s，10 mm管径的初始质量流率为914 g/s，约为4 mm管径的6.26倍，正好为其管径比的平方。再综合6 mm与8 mm管径下的结果可得出结论：初始充气质量流率与充气管径的平方呈正比，此结论与(1)式相互印证。由于大充气管径在计算初始阶段质量流率较大，相应地，图11(b)中气囊体积的膨胀速度也更快，囊内压强达到工作压力的时间也越短，10 mm的充气管径仅需要0.071 s，就可将40 L气囊充满并达到工作压力。

图11 不同充气管径下气囊充气仿真结果Fig.11 Simulated results of airbag inflation under different inflation diameters

进一步增加管径分别为2 mm、3 mm、5 mm、7 mm、9 mm的5种工况进行仿真分析，将不同工况下气囊完全展开时间绘制成图12所示的气囊完全展开时间随充气管径的变化曲线。由图12可见，气囊完全展开的时间随充气管径的增大而减小，当管径在2～5 mm范围内时，气囊完全展开时间减小得较快；当管径在5～10 mm范围内时，气囊完全展开的时间较短，且随着管径的增加其减小得越慢。进一步比对可发现在2～10 mm范围内，气囊完全展开时间与充气管径的平方呈反比。在水下气囊带动航行体上浮过程中，管径过大会造成气囊充气过快，若囊内压强远高于外界水压，囊布有可能发生破坏；若管径过小，气囊展开时间较长，航行体存在无法上浮的可能，因此在实际应用中需要合理地选择充气管径。

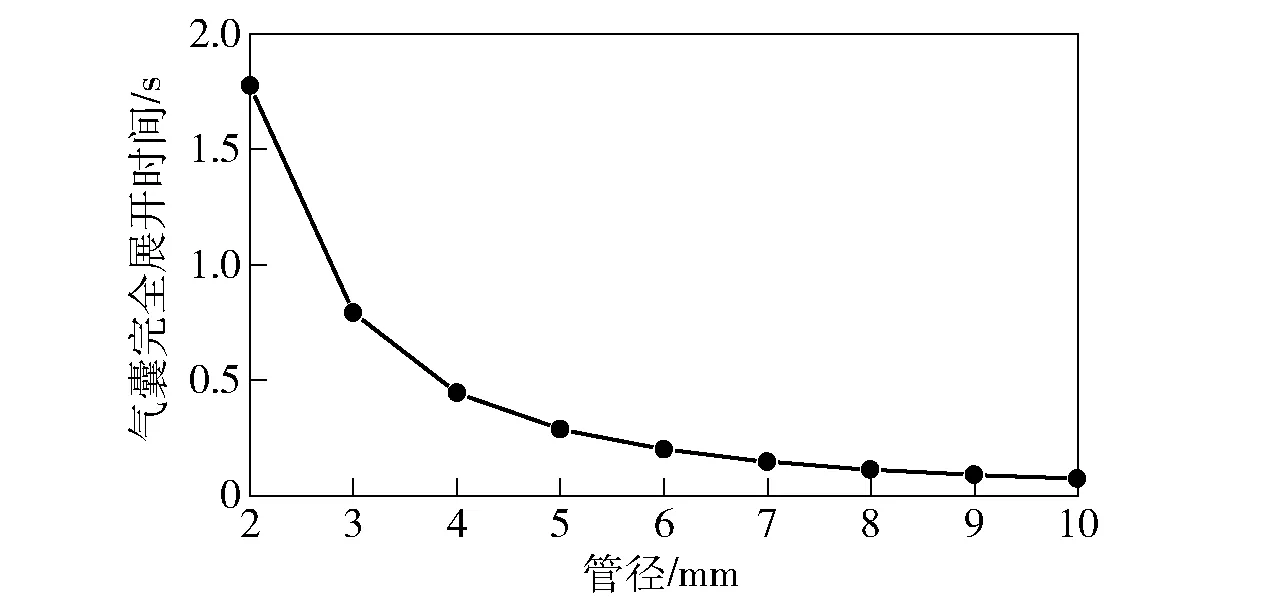
图12 充气管径对气囊展开时间的影响规律Fig.12 Influence of inflation pipe diameter on deployment time of airbag

4 环境因素对展开过程的影响分析

通过绝热条件下的仿真过程发现，气囊和气瓶在展开过程中温度大幅度降低，由气体状态方程可知，在气囊内气体的质量和压强恒定时，温度越低，气囊膨胀后的体积越小，因此在展开过程中还需要考虑展开系统与外界的热交换作用。以气囊为例，展开过程中热量从囊布外侧流体中传到囊内流体中的过程为传热过程[19]。所传递热量的计算公式为

Ere=Arek(Te-Ta)=ArekΔT，

(11)

式中：Are为传热面积(m2)；Te为环境温度；ΔT为囊内外流体间温差；k为传热系数(W/(m2·K))，它等于ΔT=1 ℃、Are=1 m2时热流量的值，是表征传热过程强烈程度的标尺。

在展开过程中考虑囊内外的传热过程，t+Δt时刻气体内能(9)式可化为

(12)

式中：Ere,t为t时刻囊内外所传递的热量。此时由(10)式可求出t+Δt时刻囊内气体的压强，完成气体状态的更新。

由图10可知，在25 MPa充气压力、10 mm管径条件下求出绝热条件下气囊的极限工作深度为95 m. 现考虑传热作用，取气瓶、气囊与外界的传热系数分别为10 W/(m2·K)、50 W/(m2·K)，环境温度为293 K，对绝热条件下气囊无法完全展开的水深100 m、120 m、150 m进行仿真，结果如图13所示。由图13可知：传热作用使得充气过程基本完成时囊内温度升高，体积继续膨胀；在100 m、120 m水深工况下囊内温度在10 s内可升高至250 K，体积达到40.1 L；在150 m水深工况下气囊温度10 s内最高可升至246 K，体积膨胀至33 L. 由此可见，展开系统与外界的传热作用会进一步增大气囊膨胀体积，提高气囊的极限工作深度。

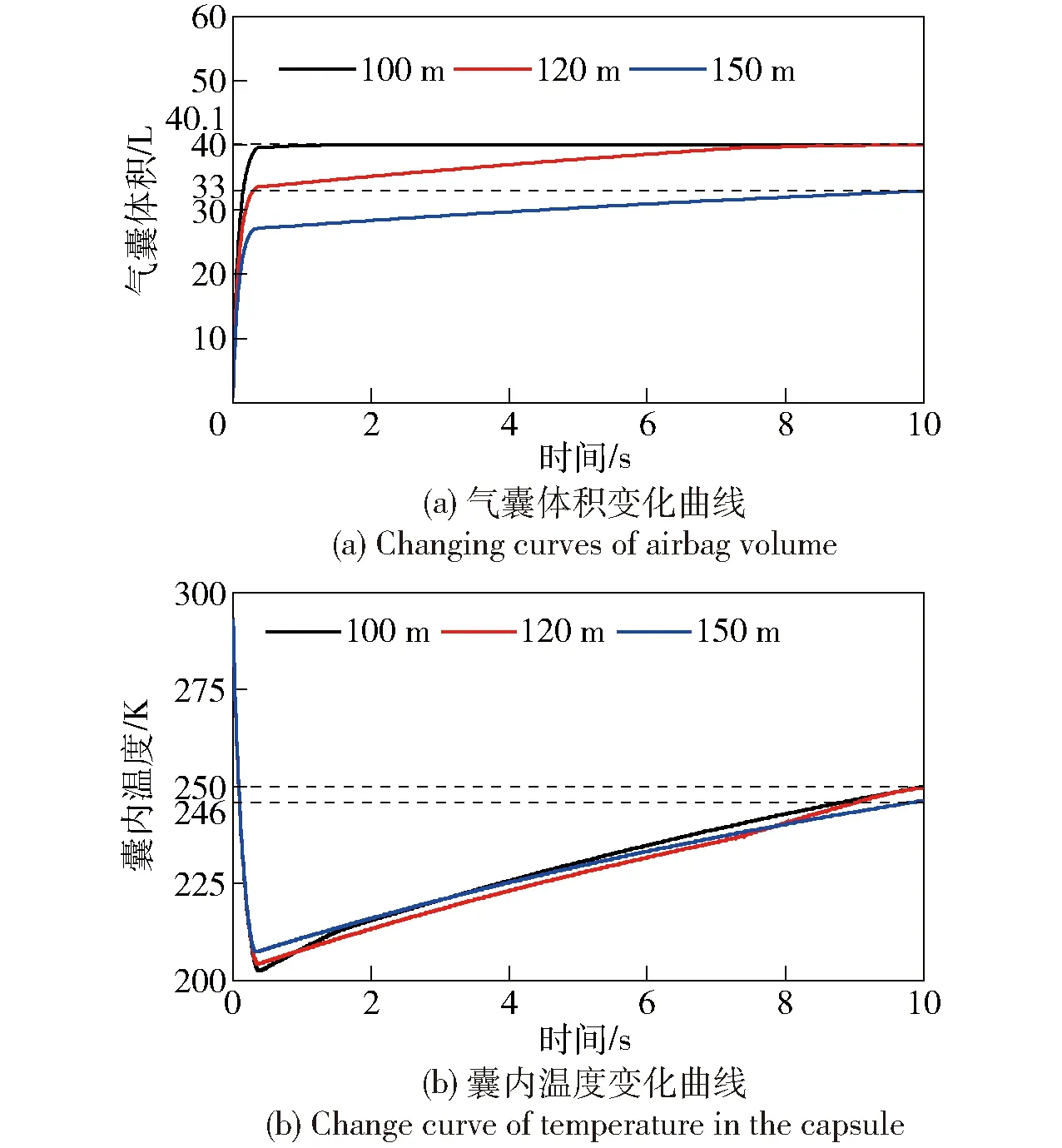
图13 不同水深工况下气囊各参数变化曲线Fig.13 Changing curves of airbag parameters at different water depths

由于展开系统中气瓶表面积较小，与外界环境之间的传热系数也较小，展开系统与外界的传热主要是依靠气囊与外界环境进行的。仿真中取气瓶与环境的传热系数为10 W/(m2·K)，气瓶与气囊的环境温度均为293 K. 计算120 m水深且气囊与外界环境的传热系数分别为30 W/(m2·K)、50 W/(m2·K)、90 W/(m2·K)时气囊的展开过程，结果如图14所示。由图14可以发现，由于气囊与气瓶之间的充气过程较短，传热作用对这一阶段的影响可忽略掉。当气瓶与气囊之间充气基本平衡后，气囊温度和体积随时间线性增加，当囊布完全展开后囊内压强升高，囊布发生变形，体积和温度增长变缓，直至气囊完全展开，达到工作压差(50 kPa)后排气口打开，其体积和压强保持不变；在传热作用下温度继续升高，直到与外界温度相等。仿真结果表明：当传热系数为30 W/(m2·K)时，气囊在10 s内最大膨胀体积为39.2 L；传热系数为50 W/(m2·K)、90 W/(m2·K)时，气囊可在10 s内膨胀至40 L.

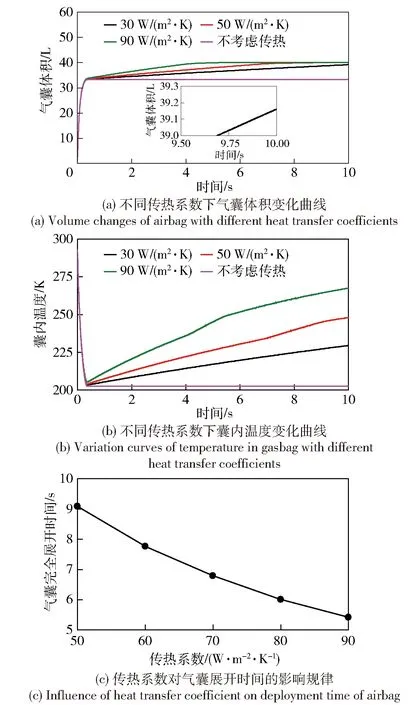
图14 不同传热系数下气囊仿真结果Fig.14 Simulated results of airbag with different heat transfer coefficients

在传热系数为50～90 W/(m2·K)范围内模拟气囊展开过程，得到图14(c)所示气囊完全展开时间的变化规律，可以发现气囊完全展开时间随着传热系数的增加而减小。综合图14可以看出，充气前期由于充气速度较快，传热作用不明显，后期气瓶与气囊之间的充气过程已基本完成，气体状态变化主要是在传热作用下产生，传热系数越高，囊内温度上升越快，体积上升也越快，充气时间越短。因此，针对实际应用中绝热条件下气囊展开体积接近设计体积的情况，可考虑传热作用对其的影响或者设置一定可放出热量的人工装置，使气囊完全展开以满足工作要求。

5 结论

本文以水下环形气囊为研究对象，对气囊在水下的展开过程进行了有限元分析，得到了气囊与气瓶在展开过程中各细节参数随时间变化规律。得出主要结论如下：

1)不同充气压力对气囊展开过程影响的研究结果表明：展开系统的充气质量流率随着气瓶初始压力的升高而增大，当气瓶中气体的质量能满足气囊完全展开的需求时，气囊完全展开时间随着充气压力的升高而减小，且其减小的幅值也随之减小；气瓶初始压力在10～35 MPa范围时，气囊极限工作深度与充气压力呈线性增加关系。经过拟合可知，其增长的幅度为充气压力每增加5 MPa，气囊的极限工作深度大约可增加21.5 m.

2)不同充气管径对气囊展开过程影响的研究结果表明：气囊完全展开的时间随充气管径的增大而减小，当管径在2～5 mm范围内时，气囊完全展开时间减小得较快；当管径在5～10 mm范围内时，气囊完全展开的时间较短，且随着管径的增加其减小得越慢。进一步比对可发现在2～10 mm范围内，气囊完全展开时间与充气管径的平方呈反比。

3)绝热条件下的仿真结果表明，气囊与气瓶在仿真过程中其内部温度大幅度降低，这可能会对气囊工作带来隐患。考虑充气过程中展开系统与环境的相互作用，研究了不同传热系数对气囊展开过程的影响规律。研究结果表明：环境与展开系统的传热作用主要发生在气囊与环境之间，由于充气过程时间较短，传热作用主要在气囊与气瓶充气平衡后进行，气囊完全展开的时间随着传热系数的增加而减小。