基于相对最值点的最小二乘直线检测方法*
肖志斌,杨 尧,史庆杰,陈国良,张 凯,苗锡奎
(1.海军装备部驻上海地区第六军事代表室·上海·200070; 2.西北工业大学 航天学院·西安 ·710072; 3.上海航天控制技术研究所·上海 ·201109; 4.光电对抗测试评估技术重点实验室·洛阳 ·471003)
0 引 言
在图像处理和计算机视觉领域中,直线作为图像的一种重要的稳定性特征,在图像分析[1]、理解[2]和三维重建[3-5]中被广泛使用,因此对其自动检测方法的研究就具有重要研究价值[6]。针对直线的自动检测,研究者提出了多种不同的检测方法。其中,Hough于1962[7]年提出了Hough变换直线检测方法,该方法以Hough变换为基础,实现了一种图像空间到参数空间的映射关系。Hough变换直线检测算法[8]首先需要通过边缘算子检测得到图像边缘,再利用Hough变换投票,在参数空间检测峰值,即可得到直线参数。此后对Hough变换算法的研究主要集中在检测的精度、计算量的改进及消除常见的“虚假直线”问题[9]。具有代表性的方法包括随机Hough变换[10](Random Hough Transform, RHT) 和概率霍夫变换(Pro-bability Hough Transform, PPHT)[11]等随机性方法。然而,基于Hough变换的直线检测算法占用空间大,实时性差,易产生虚假直线,不便于实现自动检测。故此,Burns[12]等提出了基于像素点梯度方向的直线提取算法,通过计算像素点梯度值及方向来判断直线边缘,提高了算法检测的效率,但该方法存在过检问题。Rafael[13]在Burns的基础上引入了直线支撑域的概念,提出了新的直线检测算法(Line Segment Detector,LSD)。该算法能在线性时间内得到亚像素级准确度的直线段检测效果,错误检测数量可控,且不需要调整参数,算法性能非常优秀。另外一类直线检测算法利用边缘跟踪开展直线检测,根据相连边缘点的共线性得到拟合直线。该类方法是直线检测最直观也最简单的做法,典型代表是Nevada等提出的启发式连接算法[14],但其面对分叉和断裂的效果不好。由Mansouri和Nelson等人[15]提出的基于假设检验策略的直线提取方法则先根据局部信息假设存在有一定长度的直线,然后利用全局信息来证实假设。与启发式连接算法相比,它仅在直线断裂的消除方面有所改进。
本文提出了一种新的基于相对最值点的直线检测算法。该算法属于边缘跟踪直线检测算法,但不同于传统边缘跟踪直线检测算法的是该算法并不直接利用Canny边缘,而是利用边缘的包络开展直线检测。由于包络曲线为闭合曲线,因此其具有无分叉的特点,在包络曲线上搜索相对最值点,便可定位直线端点,实现直线检测。相对最值点是本文提出的一种新的特征点,其具有一定的旋转和尺度不变性,闭合曲线上的直线的两端点必为相对最值点。并且必为一对相邻的相对最值点。针对相邻的最值点的包络像素进行最小二乘曲线拟合,根据拟合直线的方差和长度之比,便可检测出准确的直线段。
1 基于相对最值点的直线检测原理
1.1 相对最值点
如图1所示,可以通过如下办法很容易寻找到矩形的四个顶点,并找到矩形的四条直线边。首先取矩形ABCD上任意一点O,搜索矩形上距离O点最远的点,可以看出顶点C为到O点距离最远的点。

图1 应用距离最大值的矩形四顶点搜索示意图Fig.1 The four vertexes of the rectangle can be found by searching the maximum distance
然后继续寻找到顶点C距离最远的点,即为A,连接AC,搜索AC之间的矩形区域距离直线AC最远的点,结果显然是B。同样搜索CA之间的矩形区域距离直线AC最远的点,结果显然是D点。然后,继续搜索AB线段上到直线AB距离最大的点,BC线段上到直线BC距离最大的点,CD线段上到直线CD距离最大的点,DA线段上到DA距离最大的点。上述的最大距离都为0,这样就可以停止搜索,可以确认除了最开始选取的点O,其他四个点就是矩形的四个顶点,AB、BC、CD、DA为直线段。
如图2所示,在XOY坐标系下,对于任意连续曲线L:y=f(x),x∈[x1,x2],A,B为该曲线的两个端点,坐标为(x1,y1),(x2,y2),建立新坐标系X0O0Y0。其中,X0轴为连接曲线两端点的直线,X0轴为水平方向,设定垂直X0轴的任意一条直线可为Y0轴,X0轴与Y0轴的交点为坐标系X0O0Y0原点。在坐标系X0O0Y0下,该曲线上的点(x0,y0)∈L到X0轴的距离d为
(1)
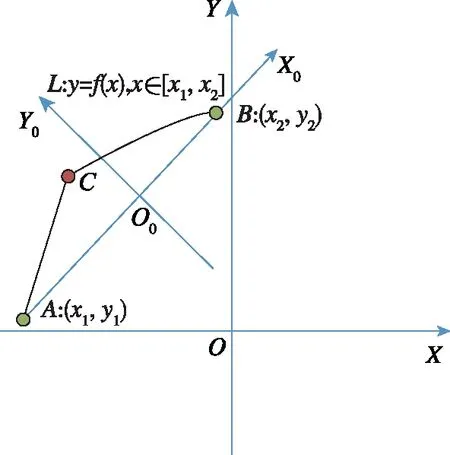
图2 相对最值点示意图Fig.2 Diagram of the relative maximum point
显然,除与X0轴平行的线段上的点外,其中距离最大值点必是坐标系X0O0Y0下的最值点。如果最值点可导,那么该点为X0O0Y0坐标系下曲线L的极值点;如果最值点不可导,那么该点必定为曲线L的间断点,本文将此类点命名为曲线y=f(x),x∈[x1,x2]的相对最值点。
上述定义表明相对最值点只与曲线形状相关,其在曲线上的相对位置具备旋转不变性和尺度不变性。显然,矩形的四个顶点为相对最值点,而在实际图像中,边缘曲线包含的直线段两端点一般为间断点,因此可通过边缘曲线端点构建X0O0Y0坐标系,利用点到坐标系X轴距离最大值进行搜索,便可定位曲线中的相对最值点。如图3所示,对于闭环曲线L:y=f(x),首先取L上任意一点A,求取L上距离A最远的点B,进而继续求取L上距离B最远的点C,此时BC两点将L分为曲线BC和CB,求取曲线BC到BC直线距离最远的点D,以及曲线CB到CB直线距离最远的点E,曲线L此时被CDBE四点分为四部分,继续针对四部分用相邻相对最值点进行最大值搜索。如果距离最大值均小于阈值ε,且对应的相对最值点对之间的曲线长度大于阈值d,则可认为该线段为疑似直线段(如CD和EC),而剩下的则得到曲线DB到直线DB距离最远点G和曲线BE到直线BE距离最远点H。这样利用前步选择的相对最值点为端点,通过迭代搜索可以更快地搜索到所有相对最值点,直到搜索的曲线段满足距离最大值小于阈值ε或曲线长度大于阈值d,即完成搜索。
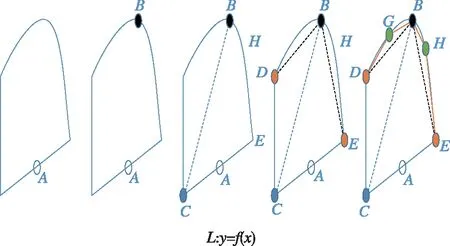
图3 相对最值点搜索过程示意图Fig.3 Searching process of relative maximum points
针对疑似直线段开展最小二乘拟合,进一步精确得到该直线的表达式、长度,以及拟合方差。将拟合方差与直线段长度之比(即细长比)作为直线判断的最终依据。
然而这种搜索方式仅可针对闭曲线,且在该曲线所围成的区域连通时才具有有效性,这是由于只有这样才能保证相对最值点顺序连接的闭曲线能够将原闭合曲线表达为由直线段构成的多边形,结构特征不会发生变化。
1.2 直线检测原理
在检测时,首先利用边缘检测算法给出图像的边缘,边缘检测的经典算法有Sobel算子[16]、Prewitt算子[17]、Roberts算子[18]等,这些经典算法原理简单、易于运行,但抗噪性能差,提取的边缘粗糙。Canny算法[19]将边缘检测问题转化为求取图像梯度函数极大值的问题。该算法能够满足最优准则的边缘检测算法,具有定位精度高、边缘检测准确等优点,且可利用Canny边缘检测算法检测出图像的边缘为单边缘,因此本文采用Canny边缘检测算法作为边缘提取算法,图4所示为Canny边缘提取后的效果。

图4 Canny边缘提取图Fig.4 Effects of Canny edge extraction algorithm
由于本文以闭合曲线为基础开展相对最值点提取,因此需要求取Canny边缘的闭合包络,这里采用一种8邻域搜索模板对边缘像素进行包络搜索,目标边缘像素位于9号位,其他8邻域位置编号如图5所示。

图5 搜索模板图Fig.5 Searching template
每一个边缘像素的8邻域像素除了邻接边缘像素外,都属于其包络,搜索过程如图6所示。
如图6(a)所示,边缘像素为9号位,初次搜索从1号位开始,围绕边缘像素按位置顺序搜索边缘包络。一种情况是,如果搜索到重复的位置,即以前搜索过该边缘像素的这一位置,那么停止这条边缘的搜索,表明包络搜索完毕;另一种情况是,搜索遇到新的边缘像素,如果该像素位置为A,即将9号位移至新的A位置开始新的搜索,图6(a)中A为6号位,图6(b)新9号位就位于图6(a)中的原6号位。图6(b)新的起始搜索位置B与图6(a)的位置A相关,表1即是位置A与位置B的对应关系,那么图6对应的新的搜索位置为4号位。通过上述搜索,最终可获得如图6(c)所示的边缘闭合包络。
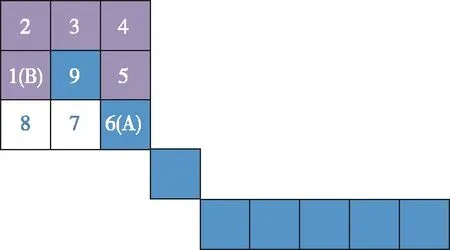
(a)重复边缘像素搜索包络
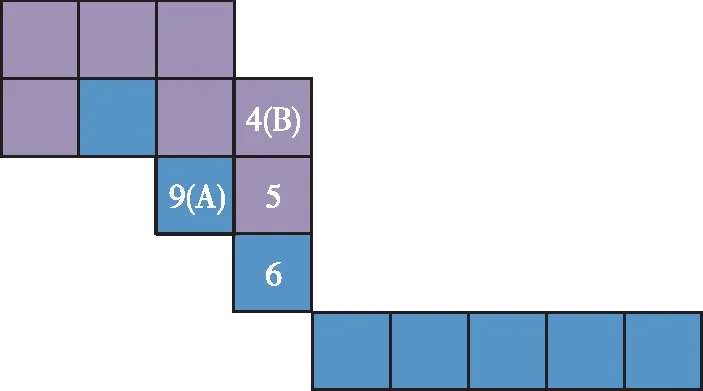
(b)新边缘像素搜索包络

(c)完整搜索边缘闭合包络图6 搜索边缘闭合包络示意图Fig.6 Closed envelope of edge pixels in searching

表1 边缘像素位置A与起始搜索位置B对应关系表Tab.1 Corresponding relationship between position A of edge pixel and position B of starting point in searching
对于图4所示的Canny边缘,其边缘闭合包络搜索效果如图7所示,这样形成的包络就为闭环的曲线,该曲线所围成的区域即为连通域。
然后利用节1.1所述方法迭代搜索每一个边缘包络的相对最值点,如图8所示。

图7 搜索边缘包络效果图Fig.7 Edge envelope after searching

图8 Canny边缘闭合包络相对最值点搜索效果图Fig.8 Searching effects of the relative maximum points of closed envelope of Canny edge
图8中的红点即为相对最值点,从图8可以看出,每一条直线的端点和不连续点均可被搜索出来,并且曲线也被相对最值点分割成小线段。利用相邻相对最值点对的长度就可以筛选出疑似直线段,即如果相邻相对最值点之间的包络线段不够长,则抛弃这一对相对最值点,剩下的相邻相对最值点对之间的线段即为疑似直线段。如图9所示,相对最值点筛选出疑似直线端点对为图8筛选后的疑似直线端点对。

图9 相对最值点筛选出疑似直线端点对Fig.9 End point pairs of possible line segments after screening
对疑似直线段进一步进行最小二乘拟合,以拟合方差与直线段长度之比作为直线筛选的最终依据。最小二乘直线拟合采用OpenCV自带的函数fitline实现,这是由于人对于直线的判断是一种相对量,具有一定的主观因素,而方差是一种绝对量。图10所示为两种拟合方差一样的曲线a和b。

(a)

(b)图10 直线判断标准示意图Fig.10 Criteria for judging straight lines
其中,曲线b远短于曲线a。从图10可以看出,曲线a通常可以认为是直线,曲线b则不行,因此在判断直线中本文以细长比作为直线判断依据,直线检测结果如图11所示。

图11 Canny边缘闭合包络直线检测效果图Fig.11 Line detection effects of Canny edge closed envelop
由于采用的是基于边缘包络的搜索,因此形成的是双直线,为此利用直线包络对应的边缘就可将双直线合并,得到如图12所示的直线检测的最终结果。

图12 Canny边缘直线检测效果图Fig.12 Effects of Canny edge line detection
从图12可以看出,本方法能够直接检测直线段,检测位置精度较高,但容易将椭圆等弧度较小的部分误认为是直线。
2 实验结果与讨论
为进一步验证本算法的性能,本文将采用Microsoft Visual Studio 2017和openCV3.4.1实现本文提出的相对最值点直线检测法,并与经典传统算法的检测效果和检测时间进行比较。计算机系统为Windows 7,CPU为Intel©CoreTMi5-4200U,CPU主频为1.60GHz,内存为8GB。
首先,利用OpenCV自带的LSD、PPHT方法对下列图进行直线检测,并与本文提出的相对最值点直线检测法的检测结果进行比较,比较结果如图13所示。

(a)大楼(512×320)

(b)道路(480×320)

(c)棋盘(320×320)

(d)相对最值点直线检测法检测效果
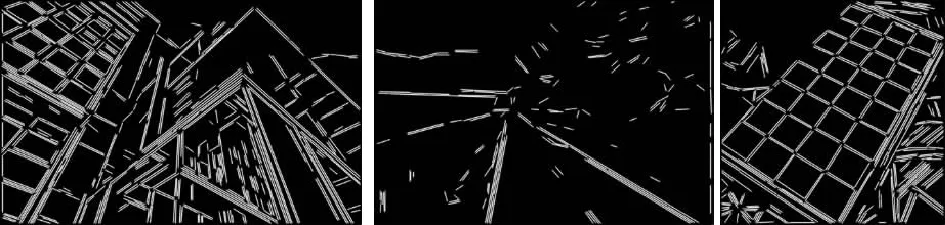
(e)LSD直线检测效果

(f)PPHT 直线检测效果图13 相对最值点直线检测法、LSD、PPHT 直线检测效果比较Fig.13 Comparison of the results of line detection of relative maximum point, LSD and PPHT
从图13的检测结果可以看出,PPHT检测效果不如LSD和相对最值点直线检测法,而相对最值点直线检测法相比LSD算法,检测更为精准,这体现在对图中道路、树木和棋盘周边的检测中。LSD算法比相对最值点直线检测法检测的错误直线更多。
进一步使用上述3幅图像的5种不同分辨率图作为测试数据集,分别对PPHT算法、LSD算法、相对最值点直线检测法进行检测速度比较。这里的速度仅指直线检测速度,不包括Canny边缘检测部分的耗时。为尽可能减少Windows系统对算法检测时间的干扰,每幅图的每种算法需运行40次,取其检测速度峰值填入表中,其结果如表2所示。
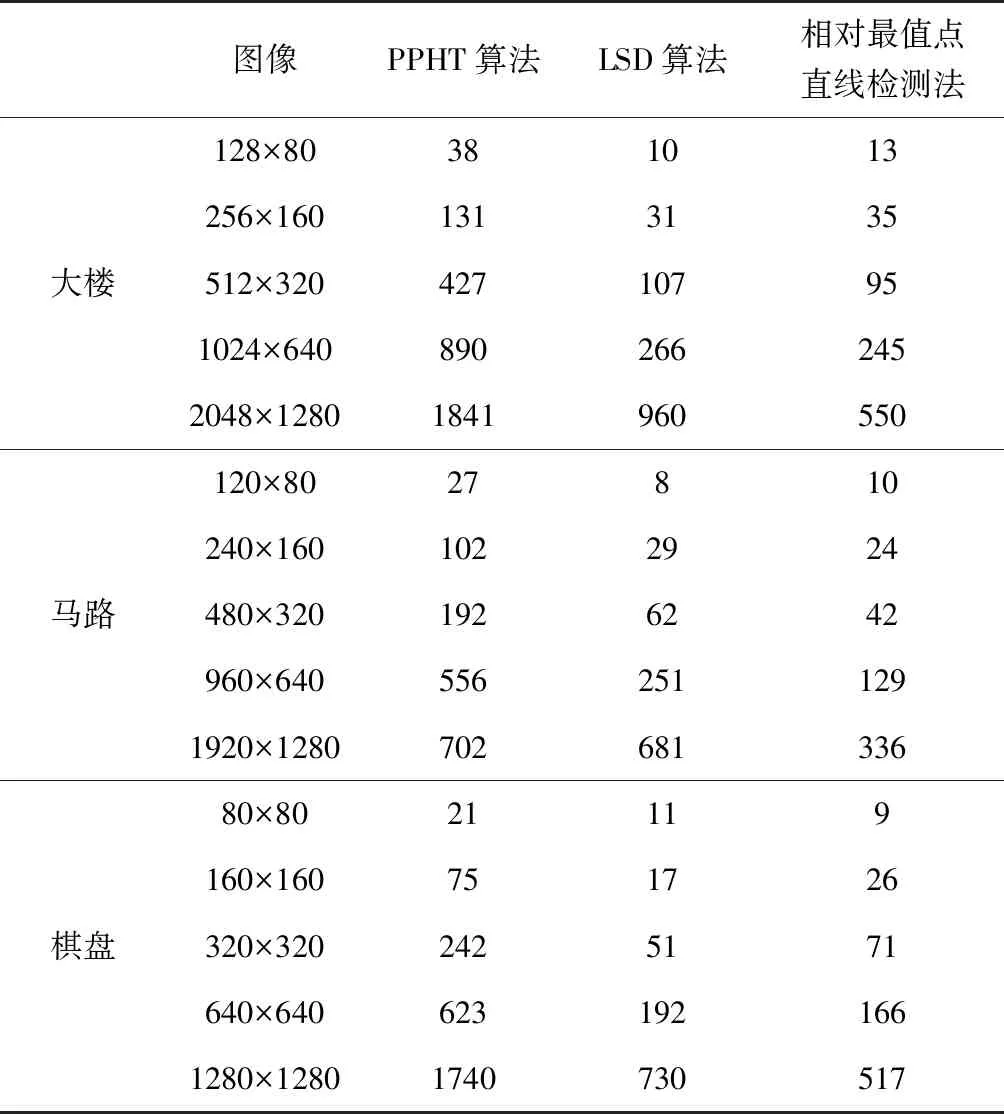
表2 直线检测时间对比表(单位:ms)Tab.2 Comparison on line detection time of the three algorithms (unit: ms)
从表2可以看出,PPHT检测速度最慢,LSD与相对最值点直线检测法在检测低分辨率图像时检测速度基本一致,但是随着分辨率的增加,相对最值点直线检测法的检测时间比LSD算法少得多。在各组图分辨率最高的情况下,相对最值点直线检测法在最快时甚至比LSD算法快1倍以上,这是由于相对最值点直线检测法针对线特征进行直线检测,随着分辨率的增加,直线长度增加近似为分辨率增加倍数的1/2次方,因此其检测耗时增加慢于图像分辨率的增加速度;而LSD算法实际处理的是面特征,其速度与像素的增加呈线性增长关系,因此随着分辨率的增加,两者之间的检测速度差异会越来越大。
3 结 论
本文提出了一种全新的直线检测方法。相对最值点直线检测法,该方法基于边缘闭合包络的相对最值点开展直线检测,对相邻相对最值点间的闭合包络曲线进行最小二乘拟合,以方差与拟合直线长度之比为阈值,实现直线的检测。对于检测到的直线,将其平移至闭合包络曲线对应的边缘上以获得最终的检测结果。实验表明,本方法相对传统检测方法(如PPHT、LSD等)具有更好的检测精度和检测速度,但本方法不是一种参数自适应的算法。随着分辨率的增加,需要调整参数,以保证检测效果的准确性,同时算法效率也需进一步提高。因此,未来研究将面向参数自适应研究和算法运算性能的优化。

