基于样本分布加权跨域极限学习机的电子鼻漂移补偿

闫嘉 陈飞越 易若男 王子健

(1.智能传动和控制技术国家地方联合工程实验室(重庆)，重庆 400715；2.西南大学 人工智能学院，重庆 400715；3.西南大学 电子信息工程学院，重庆 400715)

电子鼻也称之为人工嗅觉系统，其灵感来源于生物嗅觉系统，主要用来分析、识别和检测不同气味。一般的电子鼻系统包含3个模块:传感器阵列、数据处理模块和模式识别模块。传感器阵列由不同选择性和灵敏度的气敏传感器组成，由于金属氧化物半导体(MOS)传感器具有良好的交叉敏感性、简单的调理电路以及低廉的价格等优点，使其成为构成电子鼻气体传感器阵列最为常用的传感器。数据处理模块对收集到的信号进行放大、滤波、特征提取与选择、归一化、特征空间重构等操作，以改善数据分布，提高后续模式分类的识别率。模式识别模块则通过机器学习算法实现气味信息的模式分类。

由于电子鼻在食品安全[1]、环境污染检测[2]、安检[3]、医疗[4]等领域的应用日益广泛，因而受到了学术界和工业界的广泛关注。在过去的20年间，许多的研究人员对电子鼻的结构、应用和算法进行了大量的创新。Flammini等[5]提出了一个大范围变化的高阻值传感器的低成本接口设计，该方法可以有效提高整个传感器阵列的分辨率，并且降低阵列的成本；Fernandez等[6]设计了一个具有96个MOS传感器的高冗余传感器阵列，证明了冗余的传感器信息对于提高传感器阵列的性能有一定的帮助；Dutta等[7]设计了一个具有4个MOS传感器的电子鼻，通过对茶叶顶空气体的检测，实现了5种不同工艺下烘培的不同品质茶叶的正确分类；Siyang等[8]利用电子鼻对尿液气味进行检测以诊断糖尿病；Yolanda等[9]在电子鼻的模式识别模块使用不同的模式识别算法对植物油进行分类；Yan等[10]讨论了3种特征提取方法对后续模式分类效果的影响，实验结果表明，基于动态响应的方法能精确识别常见的伤口感染病原菌；Herrero-Carron等[11]提出了一种主动和被动的温度调制算法，大量的实验结果显示，该算法具有较强的鲁棒性，能够为气体识别提高有效的数据；殷勇等[12]结合主成分分析(PCA)和Fisher判别分析研究了由13个MOS传感器构成的电子鼻对牛奶品质检测的效果。

上述方法都是要以传感器没有出现漂移为前提才能得到有效的结果。然而，在实际的工作情况中，由于传感器自身的结构参数发生改变(例如传感器中毒、老化)和气体检测工作环境因素的波动(例如温度、湿度)会导致气敏传感器出现不可预测的漂移现象，这种现象会严重破坏电子鼻系统已构建的模式识别模型，降低电子鼻的检测能力[13- 15]。从目前的研究来看，传感器漂移问题可以从两个方向来解决。一种方法是直接对漂移的数据进行校正，常用的一些漂移成分校正法有PCA[16]、独立成分分析[17]等。但是这些方法的前提是漂移数据与原始数据具有相同的概率分布，然而由于传感器漂移的非线性和不稳定性，直接校正漂移成分的方法并不适合用来解决电子鼻应用中出现的漂移问题。另一种方法是利用迁移学习算法来探求不同域之间的关系，从而实现跨域学习。简单来说，该类方法的目的是通过数据的投影转换来降低源域和目标域之间的分布差异，用源域数据训练的分类器同样可以在目标域中得到很好的效果。Zhang等[18]考虑到源域和目标域的概率分布不同，提出了领域正则化成分分析(DRCA)的子空间投影方法，该方法可以使两个域的投影子空间具有更相似的分布。在DRCA的基础上，Yi等[19]又对该算法进行了改进，称为判别域正则化成分分析D-DRCA，该算法考虑了源域数据的标签信息，进一步提高了源域数据的利用率。此外，Zhang等[20]提出了一种新的跨域判别子空间学习(CDSL)，该方法进一步保障了数据的完整性，从而有效地提高了电子鼻的分类准确率。

近些年，Huang等[21]提出了极限学习机(ELM)，由于其在分类和回归问题中的良好性能受到了大量学者的关注。由于传统的ELM只适用于处理训练数据和测试数据具有相同分布的理想情况，因此研究人员提出了多种方法对ELM进行改进，以使其可以解决图像分类问题中的域迁移问题[22- 24]。基于ELM框架，Liu等[25]提出了跨域极限学习机模型(CdELM)来处理电子鼻的漂移问题，该模型可以有效减少源域与目标域在公共子空间中的分布差异，从而获得更好的分类效果。

虽然上述方法在领域迁移问题上取得了不错的效果，但均是利用最大均值差异(MMD)作为衡量两个域之间分布差异的指标。然而，就电子鼻数据而言，最大均值差异忽略了单个样本对全局分布差异度量的贡献度，为此，文中提出一种基于样本分布加权的跨域极限学习机框架(SDW-CDELM)。该算法以基于样本分布加权的最大均值差异作为衡量领域间样本分布差异的度量，将源域和目标域数据输入基于ELM的特征空间中，然后寻找一个合适的投影方向将ELM特征空间中的数据映射到一个公共子空间，并且在投影后提高源域数据的类间可分离度，同时尽可能保留目标域数据中可用的判别信息。投影的最终目的是缩小源域和目标域之间的分布差异，使其满足一般的分类学习算法所需要的数据分布要求。

1 相关概念

1.1 极限学习机模型

给定一组训练数据集[x1x2…xN]及其对应的输出[y1y2…yN]，N为训练样本个数，xi=[xi1…xim]T∈R1×m，yi=[yi1…yin]T∈R1×n，m和n分别代表ELM网络的输入和输出节点数。h(xi)=g(x;wi,bi)，wi∈R1×L，bi(bi∈R)代表隐含层的输出，L代表隐含层神经元个数，g(·)代表激活函数,例如g(t)=1/(1+e-t)。在隐含层到输出层之间的输出权重矩阵用β∈RL×n表示。在ELM学习网络中输入权重和偏置都是随机产生的且不需要进行调整，所以ELM学习网络仅仅只需要计算输出权重。因此，ELM的模型如下所示:

(1)

s.t.h(xi)β=yi-ξi,i=1,2,…,N。

式中:ξi∈R1×n，为第i个训练样本的预测误差；P为惩罚参数；‖·‖为Frobenius范数。

从式(1)中可以得到如下等价的无约束优化问题:

(2)

式中，H=[h(x1)T…h(xN)T]T∈RN×L，Y=[y1…yN]T∈RN×d。

式(2)是一个正则化最小二乘问题。最优解β可以通过设置目标函数相对于β的梯度为零来获得，由此得到式(3):

β*-PHT(T-Hβ*)=0

(3)

式(3)的封闭解为

(4)

式中,IN和IL分别为N维和L维单位矩阵。

一般来说，对于使用ELM的分类问题可以直接通过等式(3)或等式(4)来计算输出权重，而这仅仅取决于训练数据样本数量和隐层神经元个数，所以ELM中的其他参数不会通过迭代反向传播来进行更新。

1.2 迁移学习

随着机器学习应用场景的增加，想要训练一个性能较好的机器学习模型需要大量的数据标签信息，然而标注数据是一项复杂又成本高的任务，因此大量的研究人员开始关注迁移学习问题。迁移学习的目的是利用大量已知标签信息的源域数据去解决与之相关但又不同的目标域问题[26- 27]。对于图像分类，许敏等[28]提出一种基于支持向量机(SVM)的迁移学习算法TL-SVM，该算法利用少量的目标域标签信息和大量的源域数据构建了一个性能良好的分类模型；Duan等[29]针对跨域视频检测和文本分类等域适应问题，提出了域迁移支持向量机(DTSVM)；Li等[30]基于ELM框架提出了ELM的迁移学习算法TL-ELM和一种基于核极限学习机(TL-DAKELM)的迁移模型。本文所提出的SDW-CDELM模型通过减小源域和目标域数据投影后的样本分布加权距离，来实现不同域之间的知识迁移，使得该模型能够有效地解决电子鼻应用中的漂移问题。

2 样本分布加权跨域极限学习机

SDW-CDELM框架的基本思想是:首先将源域数据和目标域数据映射到ELM特征空间中，然后求解一个最优输出权重矩阵β，该权重可以将ELM特征空间中的数据投影到一个公共子空间，在这个子空间中两个领域之间的样本分布差异尽可能满足传统的分类方法对数据分布的要求。

SDW-CDELM框架的设计主要基于以下3个方面考虑:①最小化投影后源域和目标域的分布距离;②增强源域数据的类间分离性和类内聚集性;③保持投影后数据结构不被破坏，以便在新的子空间中保留更多的可用判别信息。

2.1 样本分布加权最大均值差异

2.1.1 最小化样本加权边缘分布距离

我们希望由投影矩阵β投影后的公共子空间中，源域数据HS和目标域数据HT之间的数据分布得到修正。为了能有效反映出全局的分布差异性，且能体现出单个样本对两个领域之间的差异度量的贡献，受文献[31]的启发，文中将样本的白化余弦相似性作为加权因子引入SDW-CDELM模型中，构造基于样本分布加权的跨域分布差异度量的方法，用以衡量极限学习机子空间中源域和目标域样本的分布差异，使之尽可能减小。基于样本分布加权的跨域边缘分布差异最小化表述为式(5):

(5)

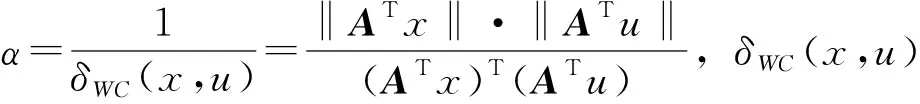
对源域和目标域数据权重向量进行如下补充:

(6)

(7)

则式(5)可以改写为

(8)

式中，

HS=[h(xS(1))h(xS(2)) …h(xS(NS))]，

HT=[h(xT(1))h(xT(2)) …h(xT(NT))]。

令H=[HSHT]，代入式(8)有:

(9)

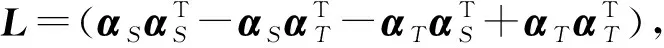
2.1.2 最小化样本加权条件分布距离

事实上，由于没有利用源域数据的标签信息，仅仅减小两个领域之间的边缘分布差异的算法往往不能得到很好的效果。为此，文中在提出的SDW-CDELM模型中加入了一个条件分布差异最小化项，以减小极限学习机子空间中源域和目标域各类样本的分布差异性之和。由于目标域样本都是未标记的，算法在运算过程中先给目标域数据赋予伪标签，然后通过迭代优化其标签。目标域数据初始伪标签由边缘分布形式SDW-CDELM模型及分类算法得到。基于样本分布加权的跨域条件分布差异最小化目标函数为

(10)

同理，将条件样本分布差异权重向量进行补充:

(11)

(12)

将式(11)和(12)代入式(10)可以得到式(13):

(13)

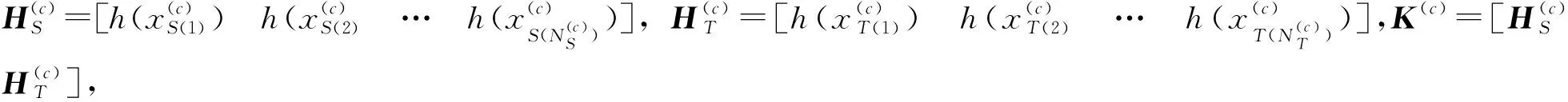
2.2 增强源域数据的类间离散性和类内聚集性

受到线性判别分析(LDA)的启发，最小化极限学习机子空间源域数据类内离散度，同时最大化类间离散度，使得源域数据的可分离性在学习的线性子空间中可以得到保证，其目标函数如式(14)所示:

(14)

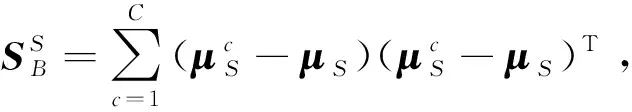
2.3 子空间数据方差最大化

为了学习最大化式(14)中的子空间β，还应确保投影不会使数据本身失真，不会破坏目标域的数据，从而可以在新的子空间中保留更多的可用信息。因此，目标域样本在新的子空间中的方差(能量)被最大化，这样目标域数据就不会失真，原始数据中的大多数可用信息都可以得以保留。目标函数为

(15)

2.4 SDW-CDELM算法求解

2.4.1 边缘分布形式SDW-CDELM模型

根据式(9)、(14)和(15)，可以得到边缘分布形式SDW-CDELM模型:

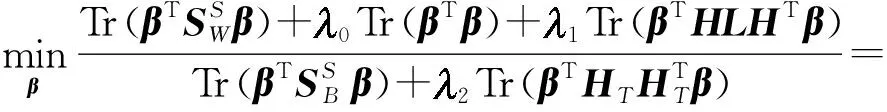
(16)

对于最小化问题式(16)，由于存在多个可行的β，因此为了得到唯一解，可以对优化问题施加一个约束项，则式(16)可以改写为式(17):

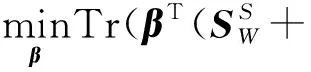
(17)

式中，η为正常数。构造拉格朗日函数:

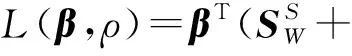
(18)

式中，ρ为拉格朗日乘子。通过设置L(β,ρ)对β的偏导为0，可以得到:

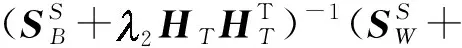
(19)

由式(19)可知，最优解β可以通过对式(20)进行特征值分解得到:

Gβ=ρβ

(20)

因此最优的投影子空间β*可以由矩阵G的前d个最小特征值所对应的特征向量表示:

β*=[β1β2…βd]

(21)

2.4.2 条件分布形式SDW-CDELM模型

根据式(13)-(15)，可以得到条件分布形式SDW-CDELM模型:

(22)

同理，根据边缘分布形式的SDW-CDELM优化过程，可以得到:

Bβ=γβ

(23)

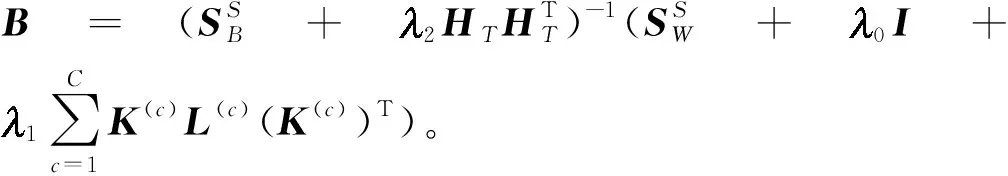
对矩阵B进行特征值分解可以得到最佳投影矩阵:

基于SDW-CDELM的漂移补偿算法步骤如算法1和算法2所示。

算法1SDW-CDELM

步骤1随机生成权重W∈RD×L，b∈R1×L并选择激活函数g(·);

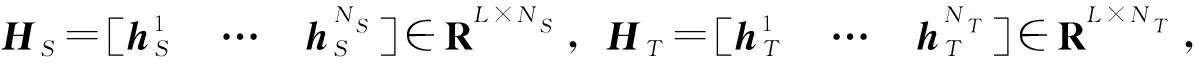
步骤4计算边缘分布差异权重矩阵L;

步骤5计算矩阵G,并对矩阵G进行特征值分解;

步骤6选取前d个最小特征值对应的特征向量构成投影矩阵β*;

步骤8计算条件分布差异矩阵L(c);

步骤9计算矩阵B并对矩阵B进行特征值分解;

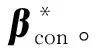
算法2分类

输入:源域数据集DS及其对应的标签YS，目标域数据集DT，子空间投影矩阵β*，隐含层神经元个数L。

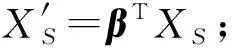
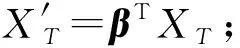
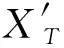
3 实验结果与分析

3.1 实验数据集介绍

为了验证本文提出的方法，采用文献[18]中所采集的电子鼻实验数据对SDW-CDELM模型进行验证。该数据集由3个部分组成:5年前采集的主板数据集和近期采集的从板1数据集和从板2数据集，其中主板、从板1、从板2是由3个相同的电子鼻系统收集。由此可见，从板数据集中不仅包含有传感器随时间老化引起的长期漂移，还包括了系统之间的板间漂移。该电子鼻系统由4个TGS系列传感器、1个温度和湿度传感器模块构成，每个样本共有6维特征。在这些数据中，包括了甲醛、苯、甲苯、一氧化碳、二氧化氮和氨气共6种气体检测数据。数据集样本详细信息见表1。

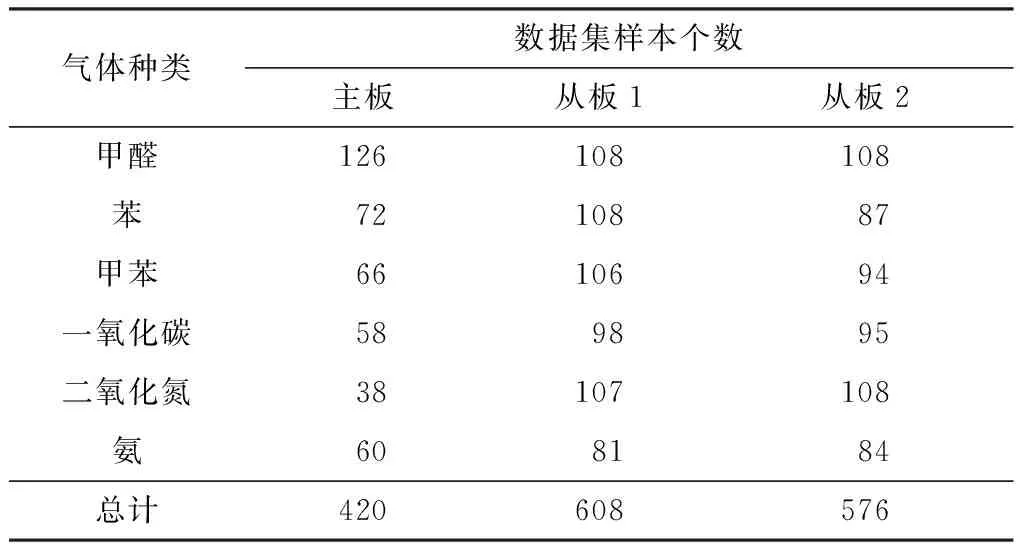
表1 电子鼻数据集分布Table 1 Distribution of e-nose data

3.2 实验设定

为了更好地验证SDW-CDELM算法的可行性，文中将SDW-CDELM与主成分分析(PCA)、线性判别分析(LDA)、支持向量机(SVM)、极限学习机(ELM)、领域正则化成分分析(DRCA)、跨域极限学习机(CDELM)、跨域判别子空间学习(CDSL)7种相关方法进行比较。将主板数据作为源域，从板1和从板2数据作为目标域。SVM和ELM作为两种基准分类器，不经过任何漂移补偿，直接用源域数据对模型进行训练，然后对目标域数据进行分类测试。对于SDW-CDELM、DRCA、CDELM、CDSL、LDA、PCA这6种子空间学习方法，将ELM作为分类器，分别计算ELM隐含层神经元个数为10和100时的识别率，并将二者中较高的识别率作为最终识别率进行对比。

使用量子粒子群优化算法(QPSO)来对SDW-CDELM、DRCA、CDSL、CDELM这4种方法中的权衡参数进行寻优，并且每种方法运算10次，求其平均分类准确率作为实验结果。其中设置量子粒子群数为60，迭代次数为200，实验结果见表2。

从表2中的对比结果来看，SDW-CDELM方法在两个任务中的识别率都是最高的，并且当利用了目标域数据的伪标签信息时，SDW-CDELM的性能最佳。这些都有力证明了本文所提出的SDW-CDELM方法能够有效地对电子鼻系统的漂移进行补偿。

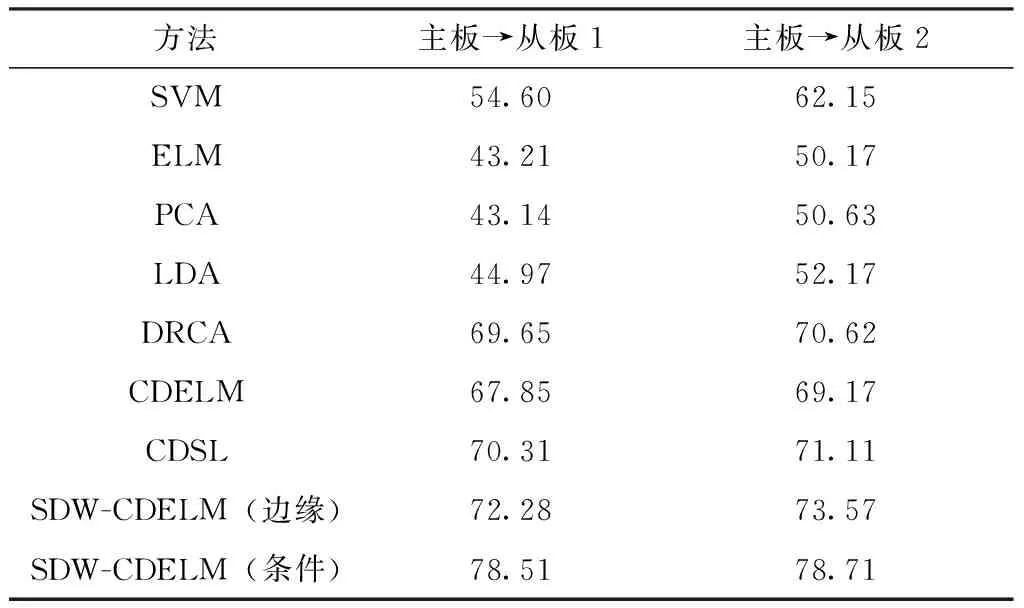
表2 不同方法的分类准确率

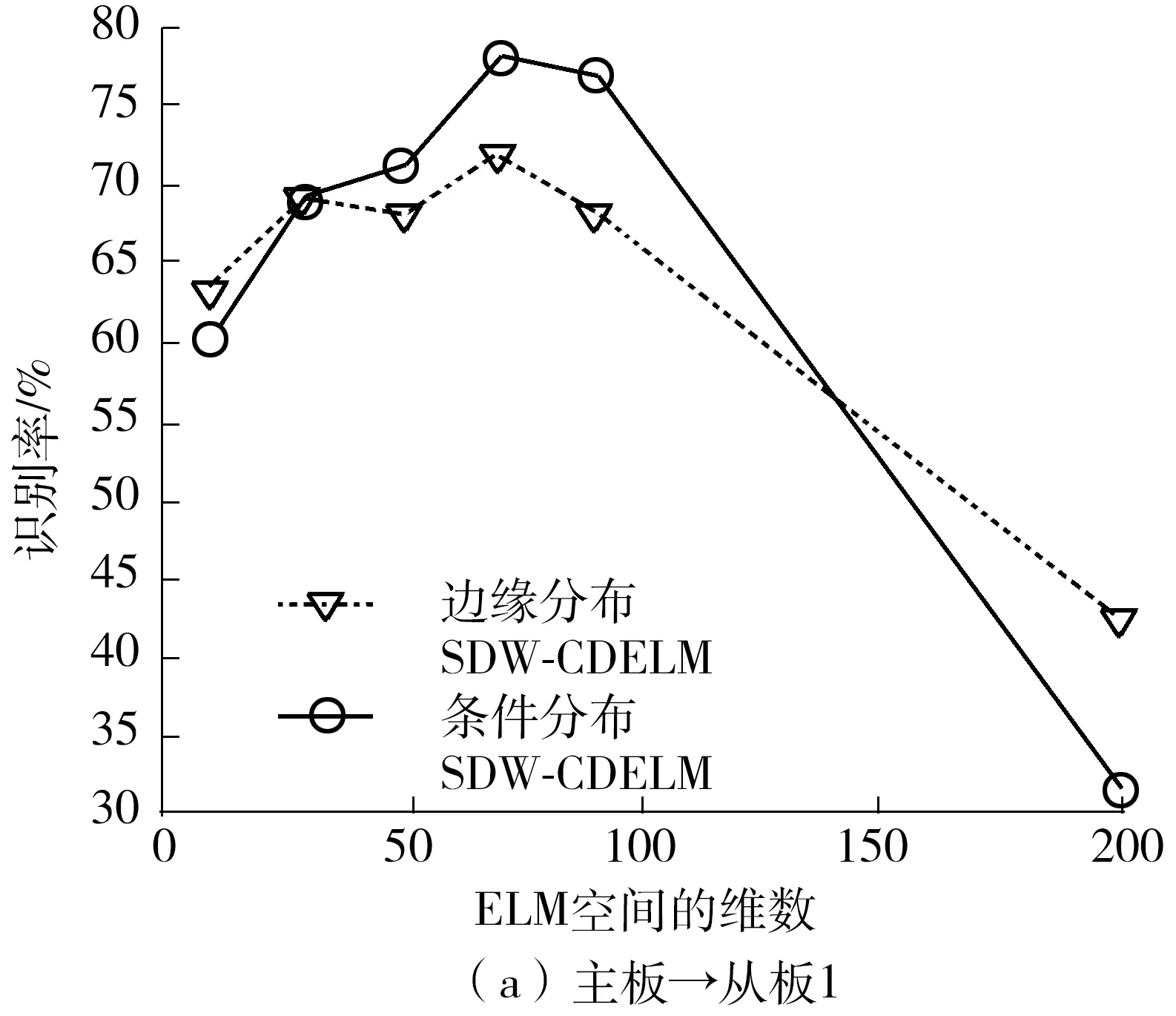
3.3 参数分析

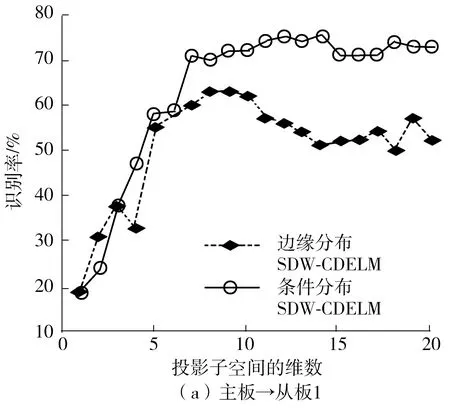
为了更好地考察模型参数对SDW-CDELM算法的影响，文中讨论在不同的参数配置下的模型性能。图1和2分别给出了不同的ELM隐含层神经元个数L和子空间维数d在上述两个任务设定下的实验结果。从图中可以看出:①ELM空间中的维度对整个模型的效果有着非常重要的影响；②在L设置较小的时候整个模型的识别率随着L的增加而上升，但当整个模型的识别率达到峰值时，模型的识别率随着L的增加而降低；③SDW-CDELM模型的识别率随着子空间维数的增加而上升。导致这种现象的原因在于:在进行域适应的过程中，我们希望找到原始数据具有较少漂移量且包含丰富分类信息的特征表达。ELM空间维数较低时，特征表达能力不足，需要将特征映射到一个更高维度的空间中去。但是ELM空间的维度不能无限升高，这样会引入冗余信息，增加数据样本中的判别信息寻找难度，当特征维度相对于数据集中的样本量来说很大时，容易出现过拟合现象，从而影响到整个模型的泛化能力。而子空间投影则相当于对ELM空间的降维，当维数过低时，导致子空间中特征信息大量丢失，当维数逐渐增大时，特征表达在抑制漂移的同时保留了大量有用信息，因此模式分类效果提高。

4 结论

针对电子鼻应用中出现的漂移问题，文中提出了一种基于样本分布加权的跨域极限学习机(SDW-CDELM)模型，SDW-CDELM在同时满足最小化源域和目标域分布距离、保留源域数据中的判别信息和维持目标域数据结构的前提下，寻找一个合适的子空间，在这个子空间中源域与目标域具有尽可能相似的分布，从而能满足传统机器学习对数据分布的要求。SDW-CDELM能够有效转移源域和目标域中的相似信息，并且SDW-CDELM能够保持较高速的运算，同时实现了具有较高精度的跨域分类。其在电子鼻漂移补偿问题上的优越性在大量的电子鼻数据集上得到了验证。但该模型仍然存在泛化能力有限，且对数据的内在信息考虑不足的问题。例如对数据的流形结构、数据与其标签之间的相关性等因素对模型表现的影响，这些将是我们下一步的研究目标。