一类含高阶非匹配扰动项的非仿射非线性系统的跟踪控制

杨浩 裴海龙

(华南理工大学 自动化科学与工程学院，广东 广州 510640)

高阶扰动在实际系统中经常出现,如轮式倒立摆[1]、无人直升机[2]和柔性机械臂[3]等。按照进入被控对象的具体形式,扰动可以分为匹配扰动和非匹配扰动。对含有非匹配扰动项的被控对象进行控制器设计所面临的难度更大,因此相关抗扰控制器的设计方法一直备受关注,并吸引了大量研究人员参与。近年来产生了不少针对非匹配扰动项的抗扰控制方法,如基于LMI的滑模控制方法[4]、H∞控制方法[5]和自适应控制方法[6]等。该类方法在抵消扰动项影响时会牺牲闭环系统的标称反馈控制性能[7]，而基于观测器的抗扰控制方法可以单独设计基于扰动观测的前馈模块与反馈控制模块,从而避免了标称反馈性能与抗扰性之间的冲突[8- 10]。

有限时间观测器(FTDO)是一种滑模观测器。在文献[8- 10]中,研究人员针对含有高阶非匹配扰动项的多种仿射系统提出了基于FTDO的控制方法,并实现了被控系统对期望固定点的渐进跟踪。然而该类方法要求被控系统具有仿射结构,且系统的相对阶需要与自身阶次相同。非仿射非线性系统在实际系统中很常见,如均质充量压缩点火式发动机[11]、大迎角飞行下的舵面控制系统[12]和超音速飞行器[13]等。针对非仿射非线性系统的常见控制方法有线性化方法、扩张状态法和基于人工神经网络与模糊控制的方法等。然而,仅在平衡点附近有效、引入奇点或运算负荷较大等因素限制了上述方法在实际系统中的应用[14- 15]。本文针对一类含有高阶扰动项的非仿射非线性系统的跟踪控制问题提出了一种基于FTDO的非线性控制器设计方法。首先构建FTDO,并通过观测输出对被控系统进行重构;之后应用一种被称为“近似动态逆”的非线性动态逆控制方法进行控制器设计,该方法作为一种基于奇异值摄动理论的非线性动态逆控制器，并没有引入奇点，且解决了反步法中常见的“复杂性爆炸”问题[14- 16]。在控制器设计过程中，首先搭建一个快变子系统以求得非仿射函数的精确逆;然后在慢时间尺度下使重构系统转换为仿射形式,并通过奇异值摄动理论确保闭环系统的跟踪性能;最后通过仿真验证了控制器的跟踪性能与有效性。

1 问题描述与准备

1.1 问题描述

考虑如下含有高阶非匹配扰动项的非仿射纯反馈非线性系统:

(1)

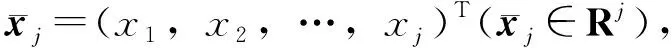
(2)

设标称系统(2)和参考轨迹yr分别满足下列假设。

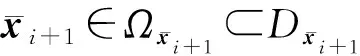
注1 假设1是近似动态逆控制器设计过程中的常见假设[14- 16]。

假设2 参考轨迹yr及其高阶导数存在且有界。

由于式(1)所具有的非仿射结构无法直接应用文献[4- 10]中基于FTDO的抗扰控制算法，所以接下来将通过近似动态逆方法为非仿射非线性系统(1)设计基于FTDO的跟踪控制器,使输出信号y在任意有限时间段内跟踪期望轨迹yr。

1.2 奇异值摄动理论

考虑具有如下形式的非线性系统:

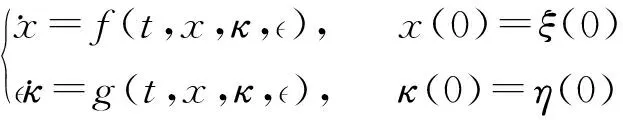
(3)

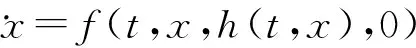
(4)

边界层子系统为

(5)

其中，e=κ-h(t,x),ξ0=ξ(0),η0=η(0)。

引理1[17]令κ=h(t,x)为奇异值摄动系统(3)对应代数方程0=g(t,x,κ,0)的孤立根。假设下列条件对于所有(t,x,κ-h(t,x),)∈[0,t1]×Dx×De×[0,0]成立:

(1)函数f、g以及它们对(x,κ,)的一阶偏导数和g对时间t的一阶偏导数连续;h(t,x)和雅克比矩阵[∂g(t,x,κ,0)/∂κ]对其自变量都存在连续的一阶偏导数;函数ξ()和η()是关于的光滑函数。

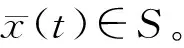
(3)式(5)表示的边界层子系统的原点是指数稳定平衡点,且在(t,x)上一致;令e⊂De为边界层子系统的吸引区,Ωe为e的紧子集。

(6)

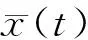
文献[16]指出,引理1中的条件(3)可以通过下面的引理2来验证。

(7)

(∀(t,x)∈[0,t1]×Dx)

则有e=0为边界层子系统的指数稳定平衡点。其中c为正常数。

2 控制器设计

2.1 有限时间观测器

针对式(1)中含有高阶非匹配扰动项的非仿射非线性系统设计如下FTDO:

(8)

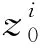
(9)

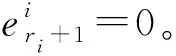
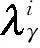
2.2 模型重构

(10)

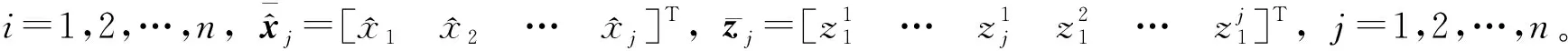
值得注意的是，式(10)中的重构系统依然是一个具有非仿射结构的纯反馈非线性系统，可将式(10)写成如下更为紧凑的形式:

(11)

(12)

2.3 近似动态逆控制器

本节将通过反步法为式(12)中的标称系统设计近似动态逆控制器。

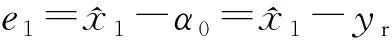
(13)

(14)

ε为待调的奇异值摄动参数,函数Q1的定义如下:

(15)

(16)

其中v1=α1-h1。根据奇异值摄动理论,令ε→0,则可以得到式(16)中奇异值摄动系统的降阶慢变子系统：

(17)

与边界层子系统：

(18)

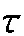
注3 从式(14)的虚拟控制量α1的动态方程中可以看出,奇异值摄动参数ε独立于被控系统的具体结构。这表明降阶慢变子系统(17)与边界层子系统(18)之间时标分离的有效性与原系统固有的时标分离特性无关。

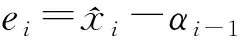
(19)

(20)

虚拟控制量αi的动态方程定义如下:

(21)

函数Qi定义为

(22)

(23)

其中vi=αi-hi。令ε→0,可以得到式(23)所对应的降阶慢变子系统:

(24)

与边界层子系统:

(25)

注4 从式(22)中可以看出,虚拟控制量的导数可以通过Qi直接得到,而无需对前面步骤中的虚拟控制量αi-1进行求导,从而避免了反步法中常见的“复杂性爆炸”问题[14- 16]。

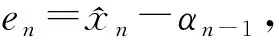
(26)

实际控制量u的动态方程定义为

(27)

函数Qn设计为

(28)

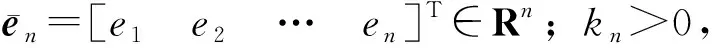
(29)

其中vn=u-hn。令ε→0,可以得到式(29)中奇异值摄动系统对应的降阶慢变子系统：

(30)

与边界层子系统：

(31)

至此,控制器设计完毕。

3 稳定性分析

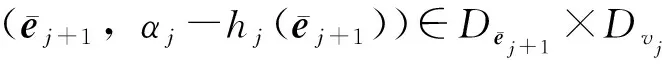
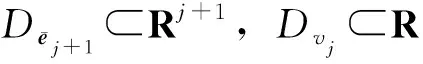
证明将式(14)、(21)和(27)构成的近似动态逆控制器代入式(10)中的重构系统,则包含FTDO和控制器的整个闭环系统可以表示为如下奇异值摄动标准型:

(32)

其中,v=[v1v2…vn]T∈Rn,q=[Q1Q2…Qn]T,h=[h1h2…hn]T,且

(33)

按照奇异值摄动理论,令ε→0,则可得到系统(32)的降阶慢变子系统：

(34)

和边界层子系统：

(35)

其中A=diag(-k1,…,kn)，为Hurwitz矩阵。

根据假设1、定理1的条件(2)可得:

(36)

由引理2可知边界层子系统在原点处局部指数稳定。根据参考文献[10],为降阶慢变子系统(34)定义有限时间有界函数(FTBF):

(37)

对式(37)求导并代入式(34):

(38)

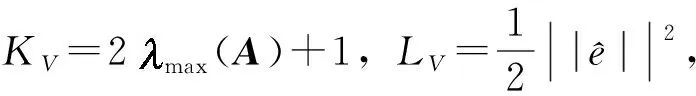
(39)

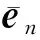
y(t)=yr(t)+O(ε)

(40)

证毕。

注5 从式(34)中可以看出,反馈增益k1,k2,…,kn将决定降阶慢变子系统特征根的位置，因此应根据控制任务对闭环动态性能的具体要求选取合适的参数。

注6 奇异值摄动参数ε应选取足够小的数值,以保证降阶慢变子系统和边界层子系统之间时标分离的有效性。此外,从式(40)中可以看出,较小的ε取值也能降低闭环系统的跟踪误差。

4 仿真示例与分析

4.1 仿真示例1

考虑如下含有高阶非匹配扰动项的非仿射非线性被控对象[16]:

(41)

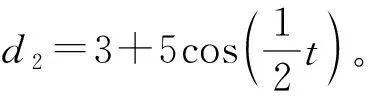
按照式(8)为式(41)构建如下FTDO：

(42)

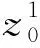
(43)

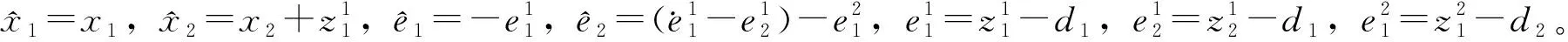
(44)

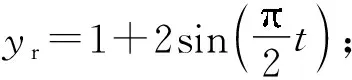
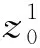
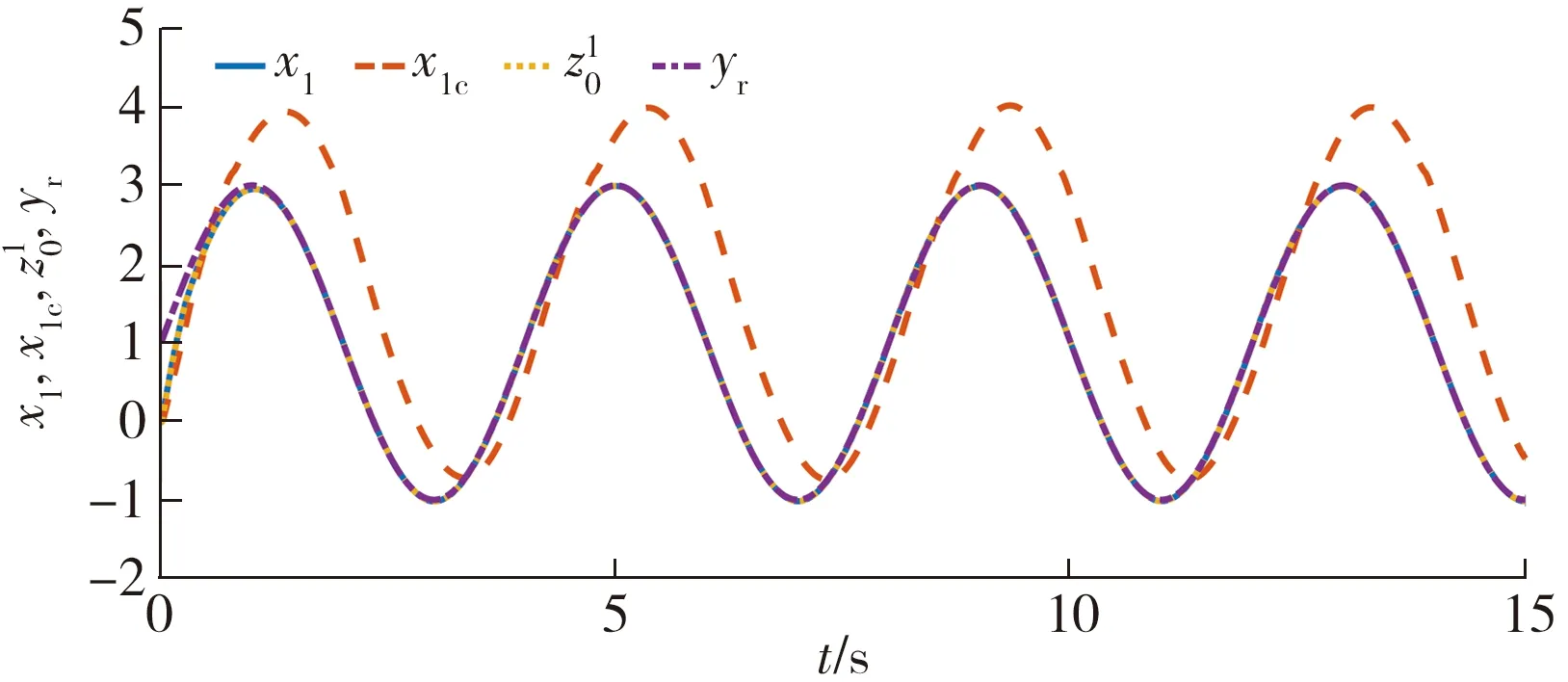
图1 x1和的响应曲线、ADI作用下的响应曲线x1c以及参考轨迹yr

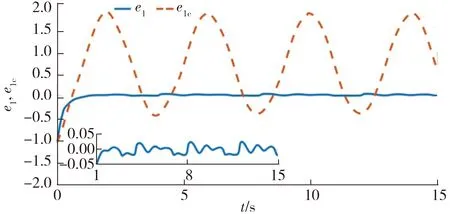
图2 跟踪误差e1和e1c的响应曲线Fig.2 Response curves of tracking errors e1 and e1c

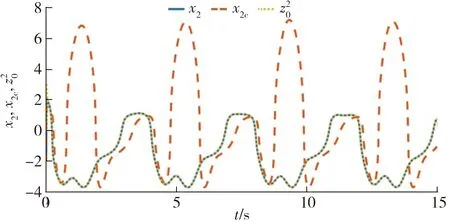
图3 x2、x2c和的响应曲线Fig.3 Response curves of x2,x2c and

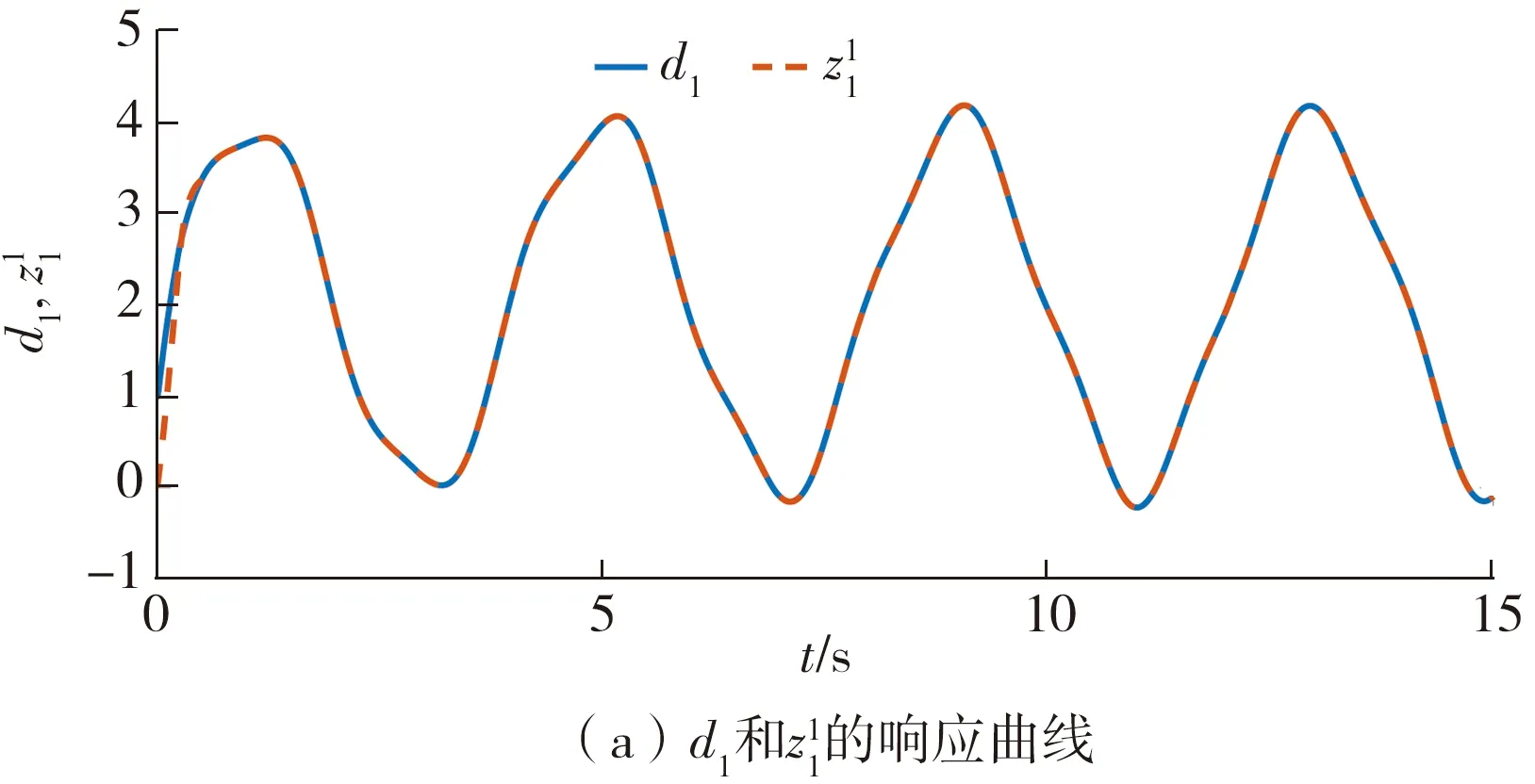
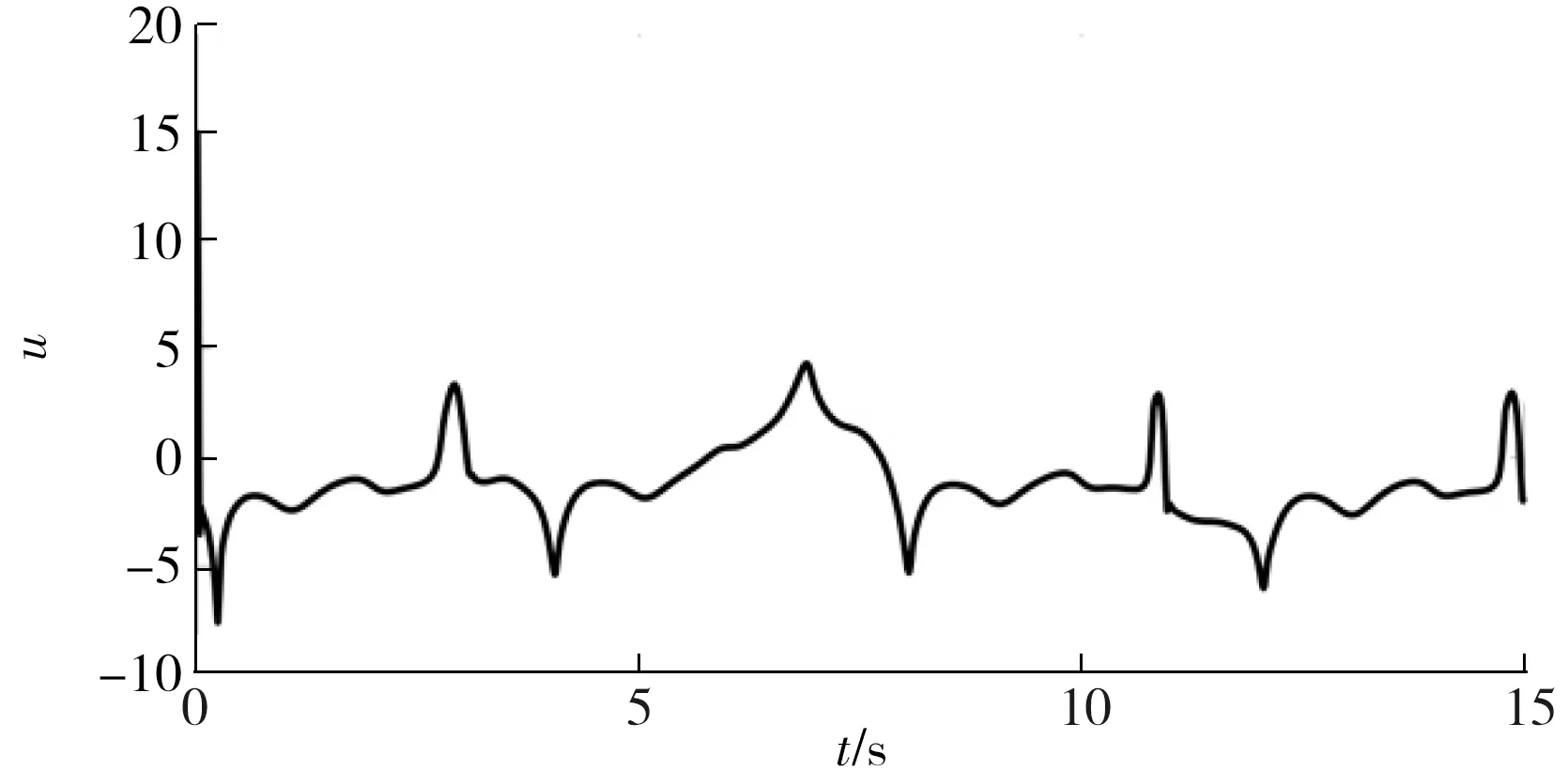
图5 控制输入曲线Fig.5 Curve of control input

4.2 仿真示例2

考虑单连杆的机电系统如下所示[18]:

(45)

从图6所示状态响应曲线可以看出,在本文控制器的作用下,即便存在高阶扰动项,系统(45)的输出信号依然可以快速跟踪参考轨迹;同时,另外两个状态也能够保持在理想的区间范围内。在图6和图7中,FTDO的观测输出能够快速、准确地跟踪各个状态变量和扰动项。图8所示控制输入的响应曲线表明本文的控制器在起始阶段快速增长，以使系统的输出误差迅速降低,并在之后进入稳定的区间,从而保证了控制效果。

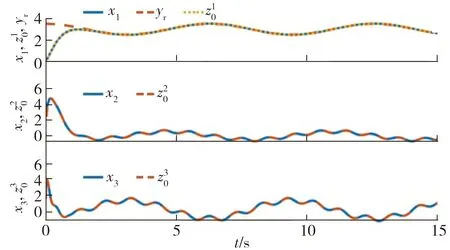
图6 状态与对应观测输出及参考轨迹的响应曲线

图7 扰动项与对应观测输出的响应曲线

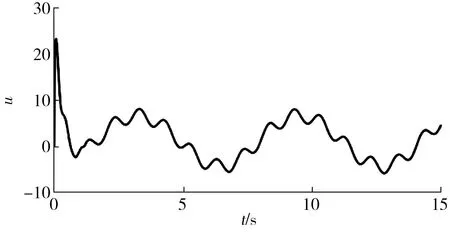
图8 控制输入曲线Fig.8 Curve of control input

5 结语

本文针对一类含有高阶非匹配扰动项的非仿射非线性系统的跟踪控制问题，提出了基于有限时间观测器(FTDO)的非线性近似动态逆控制器。针对以往研究中FTDO仅能应用于具有仿射结构的非线性系统且只能保证系统输出跟踪期望固定点的局限,本文提出的控制方法扩展了FTDO的适用范围,使其可以应用于非仿射非线性系统对时变轨迹的跟踪问题;同时本文控制器的有效性不依赖于被控系统固有的时标分离特性,并且避免了反步法中常见的“复杂性爆炸”问题。该控制方法结构简单且具有良好的可操作性,仅比文献[9]中的控制器增加了一个待调参数ε。仿真结果也验证了控制器的有效性以及观测与跟踪性能。需要指出的是,本文并未求出ε*的具体值,因此如何确定时标分离参数的边界是下一步研究的重点。