Marine Mineral Classification Based on Single-Output Chebyshev-Polynomial Neural Network

(1.School of Information Science and Engineering,Lanzhou University,Lanzhou 730000,Gansu,China;2.College of Underwater Acoustic Engineering,Harbin Engineering University,Harbin 150000,Heilongjiang,China)

Abstract: Aiming at the classification of marine minerals,an improved single-output Chebyshev-polynomial neural network with general solution(SOCPNN-G) was proposed.This model uses the general solution of pseudo-inverse to find the parameters and expand the solution space,and it can obtain weights with better ge-neralization performances.In addition,in this model,the subset method was used to determine the initial nu-mber of neurons and obtain the optimal number of the cross validation.Finally,the modified SOCPNN-G was tested in the marine mineral data set.The experimental results show that the training accuracy and test accuracy of the model can reach 90.96% and 83.33%,respectively,and the requirements for computing perfor-mance are low.These advantages indicate that this model has excellent application prospects in marine minerals.

Key words:marine mineral;classification;single-output Chebyshev-polynomial neural network with general solution(SOCPNN-G);weights;accuracy

0 Introduction

Mineral resources are divided into land resources and marine resources.At present,there is a serious shortage of mineral resources on land,which are difficult to regenerate in a short time.However,research shows that there are many kinds of metallic and nonmetallic mineral resources in the ocean,and the reserves are huge[1].In recent years,scientific research institutions and marine mining companies in various countries have been committed to the research and development of marine mining technology.Due to the rapid attenuation of electromagnetic waves in the ocean,sonar technology plays an irreplaceable role in the process of ocean mining[1].With the help of sonar technology,the use of underwater acoustic information for distinguishing between metal and rock can greatly improve mining efficiency[2].Moreover,acquiring multi-directional target signals can reduce noise interference and improve classification accuracy[2- 4].

Machine learning performs well in the fields of classification,prediction,automatic control,instance segmentation,etc.,and is developing rapidly[5- 10].There are two main components that critically affect the performance of the machine learning model:data and algorithms.On the one hand,the quantity and quality of data determine the boundary that machine learning can reach.To the best of our knowledge,there is no machine learning model which can learn from insufficient data and still performs well.On the other hand,the algorithm determines the model’s ability to extract useful information from the data.These two components are both essential and complement each other.Neural network(NN),as one of the most important algorithms in machine learning,performs well in pattern classification and has significant advantages[9].In recent years,the NN has been widely used in many fields because of its prominent advantages,such as nonlinear system modeling,self-learning and self-adjustment ability[11- 13].Researchers also use NNs to improve research efficiency and realize intelligence.The research in the ocean is no exception.Through a large number of literatures,it is found that most research in the field of ocean is carried out based on the traditional back propagation(BP) NN.However,due to its inherent defects,such as slow convergence speed,exi-stence of local minimum and weak generalization ability[14- 15],the traditional NN is not ideal in some practical fields such as ocean exploration.In order to improve work efficiency of the traditional BPNN,Ref.[16] presents a NN based on Chebyshev polynomial[17],which proves superior in pattern classification.At the same time,the gradient descent algorithm adopted in BP neural network significantly increases the computational complexity and reduces computational efficiency[14]due to its lengthy iteration.Based on this phenomenon,a large number of experiments related to weights and structure determination(WASD) algorithm[18- 19]prove that the WASD algorithm plays an excellent role in the determination of weights and network structure in the NN.

This paper proposes a method for obtaining all solutions of the equation to get all weights,which gives a large solution space and can obtain weights with exce-llent generalization ability.Based on this method,single-output Chebyshev polynomial neural network with general solution(SOCPNN-G) is proposed.In addition,in SOCPNN-G,the initial number of neurons in the data set is determined using the subset method.Moreover,the subset method is also used to obtain the optimal fold of cross validation.

The rest of the paper is organized into four sections.The theoretical bases and model structure of the SOCPNN-G are given in Section 1.In Section 2,the algorithm of the SOCPNN-G is introduced,which contains the general solution of weights direct determination(WDD) algorithm,subset method and unfixed-fold cross-validation(uFCV) algorithm method.Sonar dataset of marine minerals is described in Section 3,and experiments based on marine mineral data set are conducted to assess the performance of the SOCPNN-G in the marine mining industry.Finally,Section 4 summarizes final remarks.

1 Theoretical Basis and Model Structure

This section introduces the theoretical basis involved in the model,and then outlines the structure of the SOCPNN-G model.

1.1 Theoretical Basis

The basic theoretical knowledge used in the trai-ning SOCPNN-G model is described in detail,including the approximation of function and the graded lexicographic order algorithm.

1.1.1ApproximationofFunction

Definition1 Assume thatx∈[-1,1],

L0(x)=1,

L1(x)=x,

On the basis of polynomial interpolation and approximation theory[21],when a given continuous functionf(x) is defined within the interval [-1,1],it can be approximated by the Chebyshev polynomials as follows:

(1)

Definition2 Assume thatx∈[0,1],

is called Bernstein polynomial which is a series of polynomials used to estimate a continuous function.Bn(f,x) is called thenth order Bernstein polynomial off.Iffis continuous on[0,1],Bn(f) uniformly converges tofon[0,1][22].

Based on Ref.[22],iff(x) is a continuous real value function ofMvariables,which is defined inx=[x1x2…xM]T∈[0,1]M×1(the superscript T stands for getting the transpose of a vector),the Bernstein polynomials off(x) can be constructed as follows:

wherem=1,2,…,M.

LetPk1,…,kM(x)=pk1(x1)…pkM(xM),one has

Pk1,…,kM(x)≈

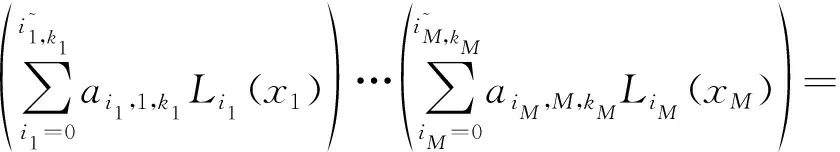
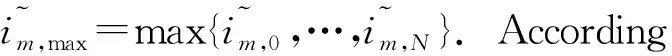
Thus,ifNis sufficiently large,

Therefore,for the objective functionf(x) of the unknown continuous real numbers defined inx∈[0,1]M×1,we could get the optimal weight {wi1,…,iM} of its basis function {Li1(x1)…LiM(xM)} to perform the optimal function approximation.

1.1.2GradedLexicographicOrder

Condition 1:|C|>|C′|;

Therefore,the best approximation to the target functionf(x) can be obtained by the following formula:

whereGis the number of basis functions for the best approximation of the target functionf(x),and {hg(x)|g=1,2,…,G} denotes the set of basis functions with the graded lexicographic order and {wg|g=1,2,…,G} is the set of weights corresponding to the basis functions.

1.2 Model Structure

The structure of the SOCPNN-G model is shown in Fig.1,which adopts a typical three-layer neural network model structure,including an input layer,a hidden layer and an output layer.

Fig.1 Model structure

The number of neurons in the input layer is denoted asM,which signifies theMattributes of the input sample.Because of the single output characteristic of SOCPNN-G model,the number of neurons in the output layer is 1.From the previous discussion,it can be seen that the number of neurons in the hidden layer greatly affects the performance of the neural network model.Therefore,the optimal number of neurons in the hidden layer is also what we need to focus on in this paper.Meanwhile,the activation functions of the input layer and the output layer are simple linear functions,and the activation functions of the hidden layer are the aforementioned basis functions {hg(x)|g=1,2,…,G}.To simplify the model,the neuronal bias of all layers is set to 0.Each connection weight between the input layer and the hidden layer is fixed as 1,and each connection weight between the hidden layer and the output layer is {wg|g=1,2,…,G}.In this paper,the determination ofwgis performed by modified WDD algorithm,which will be introduced in more detail later.Therefore,the output of SOCPNN-G can be expressed as follows:

2 Algorithm of SOCPNN-G

In this section,the algorithm used in SOCPNN-G and the improvements are described in detail.

2.1 General Solution of WDD Method

Traditional NNs use gradient descent algorithm to adjust parameters.However,it is easy to fall into the local minimum,and the NN requires multiple iterations,which is very time-consuming[14].Some scho-lars are committed to the WDD method[17-18],so as to overcome the defects of the traditional gradient descent method.A large number of experiments show that using the WDD method to determine the weight is effective and efficient.

In this paper,a method to obtain the general solution of the network is proposed to improve the traditional WDD method.Before further discussion,some descriptions of symbols are given.The training data set is defined as {(xz,yz)|z=1,2,…,Z},wherexz=[xz1,xz2,…,xzM] represents thezth training sample,andyzreveals the NN output of the sample.The connection weight matrix of the hidden layer and output layer is defined asw=[w1,w2,…,wG]T∈RG×1,activation function

On the basis of the WDD method,one can obtain the optimal weight matrix as follows[24- 26]:

w=H†y

(2)

wherey∈RZ×1is the output of the network and the superscript † denotes to get the pseudoinverse of a matrix.Equation (2) can be deemed as the unique minimum norm least squares solution of the equation.With this in mind,general form of the least square solution of the equation is presented to find the ideal weights,that is

w=H†y+(I-H†H)s

(3)

whereH†y∈RG×1,I∈RG×Gis the identity matrix,ands∈RG×1is an arbitrary vector.Equation (3) possesses the capability to obtain all solutions of the network,regardless of whether the equation is under-determined,well-defined,or over-determined.The weights calculated by the modified WDD method contain the solutions of the traditional WDD method,which enables to obtain more outputs and to determine the optimal weights in the light of the performance of the network on the validation set.

2.2 Subset Method

A large number of studies find that mental representations are improved based on experience[27- 29].Inspired by this phenomenon,the SOCPNN-G model adopts the method of subset to determine the initial number of neurons and the fold of cross validation[30].The network performance depends largely on the number of neurons[31- 33].In general,the number of polynomial approximations on a subset of a dataset is sma-ller than the total dataset[30].Therefore,we can obtain the initial optimal number of neurons by training the model with subsets,and take it as the initial number of neurons of the whole dataset.This can make training process of NN more effective and efficient.For different NN models and different experimental data,the optimal fold of the cross validation may vary in the process of training a better NN model.By using the subset method and setting the loop in the experiment,SOCPNN-G can explore the optimal fold of the cross validation without consuming too much computation time and improve the performance of the model.

2.3 uFCV Algorithm

Before introducing theuFCV algorithm in detail,the concept of the root mean squared error(RMSE) needs to be introduced,which is defined as fo-llows[34]:

whereZrepresents the size of the input data,rzsignifies the actual value of thezth input sample,and they(xz) denotes the NN output of thezth input sample.A larger value of RMSE means a larger gap between the actual value and the output of the NN,and the performance of the NN model is poorer.On the contrary,to obtain the smaller RMSE value is the purpose of NN training,so that the output of NN is closer to the real value of samples.In theuFCV algorithm,we utilize the relative relation of RMSE corresponding to different neurons to determine the fold of cross validation and the optimal number of neurons.

In the area of pattern classification,approximation and generalization performances are both important for evaluating neural networks,and they are mainly determined by the number of neurons.In the SOCPNN-G model,the number of neurons in the input layer is uniquely determined by the number of attri-butes of the input samples,while the number of neurons in the output layer is 1.Therefore,the number of neurons in the hidden layer contributes to the perfor-mance of the NN greatly.Besides,for NNs,the problem of overfitting has not been completely solved.At the beginning of network training,with the number of neurons increasing,the accuracy of training set and test set increases.When the number of neurons reaches a specific value and then continues to increase,the training accuracy will continue to raise,but the test accuracy declines,which is the phenomenon of “overfitting”.Inspired by the multiple-fold cross-validation algorithm presented by Ref.[33],in our mo-del,the folduof the cross validation is determined by using the subset method.ThenuFCV algorithm is used to determine the optimal number of neurons.

TheuFCV algorithm is mainly divided into two steps:determining the folduofuFCV,and usinguFCV algorithm to determine the optimal number of neurons.The specific steps are as follows:

Step1 Use the subset method to extract part of the training dataset and test dataset,and label them as small training dataset and small test dataset,separately.

Step2 In a certain number of loops(such asutaken in Refs.[1,15]),we use the small dataset obtained in step 1 to train the model.After the loop,output theucorresponding to the minimum RMSE as the optimal fold for cross validation.Step 3 begins to implement theuFCV algorithm.

Step3 Randomly divide the training dataset intousubsets with similar sizes.In theuth loop,theuth subset is used as the validation set and the remainingu-1 subsets are used as the training set.In the process of determining the number of neurons in each round,if the RMSE corresponding to the validation set keeps increasing in the past calculation,the cycle will be stopped,and the number of neurons corresponding to the previous minimum validation error will be taken as the output of the loop.

Step4 After theuloops,average and round the results to obtain the optimal number of hidden-layer neurons.

3 Data Set and Experiments

This section introduces the data set used,and various simulation experiments are provided and analyzed to substantiate the efficacy,superiority,and physical realizability of the proposed SOCPNN-G model.

3.1 Descriptions of the Data Set

The sonar data set provided by UCI machine learning repository is used for training,validation,and testing.This data set contains sonar signals reflected from metal and rock from various angles and can be used for the training and validation of the SOCPNN-G.Specifically,the dataset contains 208 instances with 60 attributes.The attributes in the range 0.0 to 1.0 represent the energy in a particular frequency band.In addition,after modifying the characteristic column(column 61) of the original data set,the number 0 is used to represent rock and is used to represent metal in our experiment(in the original dataset,the letter “R” stands for rock and “M” for metal).

3.2 Experiments

In the same NN model and a different data set,the optimal number of folds for cross validation in the NN may not be consistent,so the SOCPNN-G is proposed.Different from the traditional models using the fixed 4FCV,8FCV and 10FCV algorithms,subset method is used to determine the optimal foldufor cross validation.Then theuFCV algorithm is used to train the SOCPNN-G.The SOCPNN model is used to classify the sonar data set obtained from the UCI machine learning repository.In order to verify the necessity and feasibility of theuFCV algorithm,five experiments are conducted.The experimental results are shown in Table 1,where the “Fold” column indicates that the optimal folds for cross validation determined are different.Furthermore,the traditional fixed-cross validation algorithms are used to train the model on the same data set.In order to avoid accidents in the experiment,three repeated experiments are performed for each method,and the average of the three results is taken as the final result.The training accuracy rate and test accuracy rate are shown in Table 2.As shown in Table 2,for the model corresponding to the fixed cross-validation algorithm(u=4,8,10),the experimental results vary greatly each time.

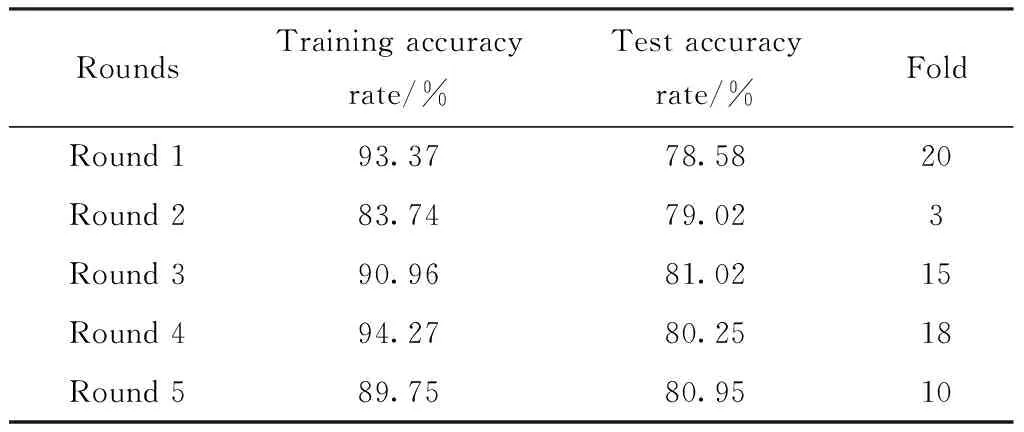
Table 1 SOCPNN-G to determine the optimal fold

Table 2 Performance comparisons of different FCV methods %

Sometimes the model performs well,while sometimes its performance is extremely poor.On the contrary,for theuFCV algorithm with unfixed number of folds,the SOCPNN-G model consistently performs well.

The subset method is also used to determine the initial number of neurons.As mentioned in Section 2.2,it is important and effective to determine the initial number of neurons of the NN.Not using the fixed initial neuron number,the subset method improves the efficiency of the NN in some situations.The superiority of the subset method is verified by experiments.As a comparison,original SOCPNN is trained that determines the initial neuron number of the NN as 1.In order to avoid accidents in the experiment,it is repeated thrice,and the experimental results are shown in Table 3,which shows that the SOCPNN-G adopting the subset method is superior to the original SOCPNN mo-del.On the one hand,the subset method is used once,but two parameters ofuFCV and the initial structure of the NN are determined,which play an important role in the performance of the NN.On the other hand,the subset method only requires a subset of the whole dataset,hence there is not much time overhead in this subset model.

With the aid of the general solution form of matrix equations,the modified WDD algorithm used in this paper can obtain all solutions with the smallest error on the training set,among which there may be some solu-

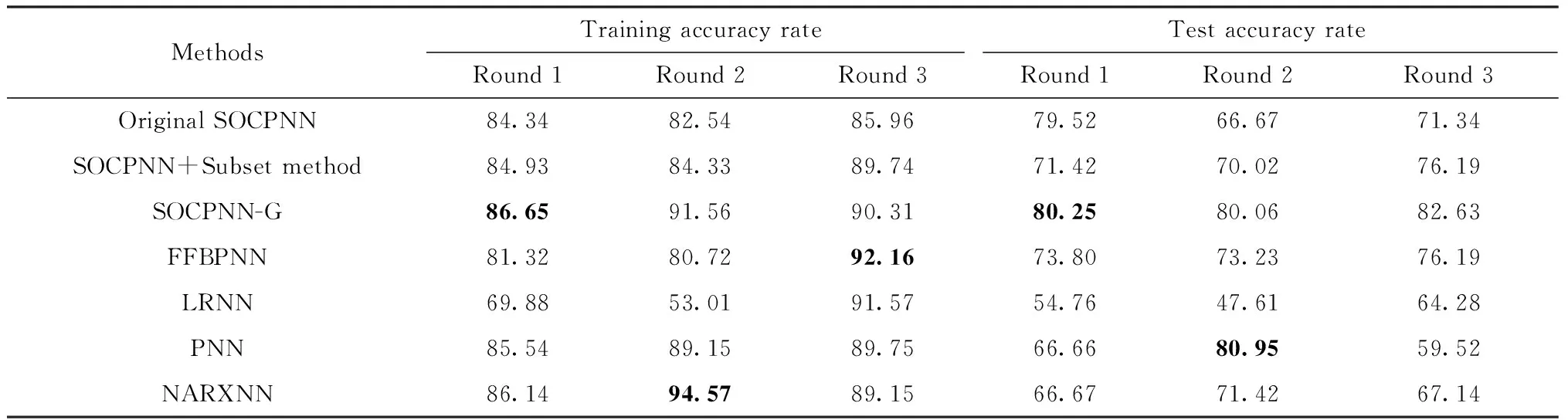
Table 3 Comparison of experiment results among different classification methods1) %

tions that are better than the minimus norm least squares solution on the validation set.Experiments corresponding to original WDD algorithm and the modified WDD algorithm are carried out,severally.In order to avoid accidents in the experiment,each experiment is repeated thrice,and the experimental results are shown in Table 3.The results show that the modified WDD method can improve the performance of NN.

After several experiments,the SOCPNN-G model performs well on the sonar data set,in which the trai-ning accuracy and test accuracy reach 90.96% and 83.33%,severally.The experimental results are shown in Fig.2.In order to evaluate the performance of the SOCPNN-G after various improvements,comparative experiments are conducted among the SOCPNN-G and other NN models.The models used for comparison are feed-forward back propagation NN(FFBPNN),layer recurrent NN(LRNN),perceptron NN(PNN),and nonlinear auto-regressive with reversible inputs NN(NARXNN).These models are used to classify the sonar data.In order to avoid accidents in the experiment and facilitate the analysis of model performance,these models and SOCPNN-G are tested three times,separately,and the experimental results are shown in Table 3,which show that the SOCPNN-G model performs best in the classification of marine mineral data sets.Therefore,the SOCPNN-G can be used for marine mineral classification and better serve the marine mining industry.All the experiments are conducted on Matlab 2019 with a computer equipped with 2.90 GHz Intel i5-9400CPU,8 GB memory.

4 Conclusion

Using the general solution form of matrix equations,the modified WDD algorithm obtaining all solutions with the smallest error has been proposed,among which there may be some solutions that are better than the minimus norm least squares solution.The modified WDD algorithm has been applied to the SOCPNN-G.With the aid of subset method,the SOCPNN-G adaptively determines the fold of cross validation and determines the initial structure of the NN.The performance of the original SOCPNN has been significantly improved in the comparative experiments.The experimental results have shown that the SOCPNN-G performs best,and the training accuracy and test accuracy reach 90.96% and 83.33%,respectively.Considering that the SOCPNN-G has higher accuracy and lower computational overhead,it has potential for application in the marine mining industry.